基于改进的多分量频率-贝塞尔变换法研究郯庐断裂带潍坊段上地壳径向各向异性结构
周桂理, 罗松*, 姚华建,2
1 中国科学技术大学地球和空间科学学院, 合肥 230026
2 中国科学技术大学蒙城地球物理国家野外科学观测研究站, 安徽蒙城 230026
0 引言
郯庐断裂带是一条纵贯中国东部大陆边缘的巨型断裂带,北起黑龙江,南至长江,在中国境内绵延 2400 km.自早中生代形成以来,郯庐断裂带历经多期次挤压、走滑和拉张等构造活动(朱光等,2018),对中国东部地区的地质构造、岩浆活动、地震活动和矿产资源分布产生了重要影响(丰成君等,2017).根据郯庐断裂带地震活动和构造特征一般又可划分为北、中、南三段.本文研究区域在郯庐断裂带潍坊段,属于断裂带的中段,位于山东北部,又称沂沭断裂带.该区域东临胶东地块,西临鲁西隆起,地质结构复杂,隆起和凹陷交错相连,主要包含汞丹山凸起、潍坊凹陷、潍县凸起和潍北凹陷等地质构造单元.内部发育有4条主干断裂,自东向西依次为昌邑—大店断裂(F1)、安丘—莒县断裂(F2)、沂水—汤头断裂(F3)和鄌郚—葛沟断裂(F4),呈现“两堑夹一垒”的构造形态(图1a).第四纪以来,郯庐断裂带进入了新的构造活动期,尤其在山东南部的活动性更为强烈,历史上发生过多次地震,包括1668年8.5级郯城大地震和公元前70年7.0级安丘地震(王华林, 1990; 马玉香和钟普裕, 2009).这些构造活动对岩石圈、地壳尤其是上地壳介质结构都进行了复杂的改造作用.但是,相比于郯庐断裂带其他区域,潍坊段历史上记载的地震较少,属于地震空区,未来发生大地震的可能性尚不明确.因此,探究现今潍坊段浅地壳深部变形结构特征可以对认识郯庐断裂带的构造活动起到一定的约束作用,为该地区的地震危险性评估提供重要参考模型.
迄今为止,众多学者对郯庐断裂带开展了大量的速度结构研究,如体波走时层析成像(黄耘等, 2011; 熊振等, 2016; Lei et al., 2020; Bem et al., 2022),面波层析成像(徐果明等, 2000; Huang et al.,2003; 易桂喜等, 2008), 背景噪声成像(孟亚峰等, 2019; Gu et al., 2019; Li et al., 2020; Luo and Yao, 2021),以及接收函数反演(Chen et al., 2006; Li et al., 2021)等.但是这些研究的研究区域通常尺度较大,不能较好地反映郯庐断裂带潍坊段小区域的精细结构特征.近年来,也有学者专门对郯庐断裂带潍坊段进行了研究.Ma等(2020)利用背景噪声两步法层析成像得到了潍坊段浅层8 km内的三维SV波速度结构,揭示了该区域有强烈的横向不均匀性; Tian等(2020)利用远震P波走时建立了潍坊段30 km深度内的三维P波速度模型; 靳佳琪等(2023)使用面波直接成像法建立了潍坊段上地壳7.5 km内的三维高分辨率各向同性和方位各向异性SV波速度结构.但是对于该地区的上地壳径向各向异性结构特征,目前仍然鲜有报道.
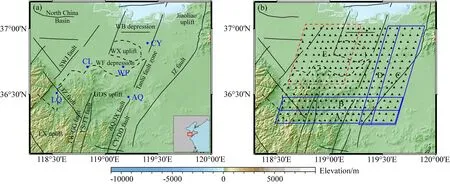
图1 研究区域主要地质构造单元分布以及台站分布(a) 研究区主要构造单元分布图. 黑色实线代表主要断裂(邓启东等, 2002): SWJ fault,上五井断裂; LJZ fault,李家庄断裂; JZ fault,景芝断裂; TW-GG fault,鄌郚—葛沟断裂; YS-TT fault,沂水—汤头断裂; AQ-JX fault,安丘—莒县断裂; CY-DD fault,昌邑—大店断裂; 黑色虚线为主要构造边界: WB depression,潍北凹陷; WX uplift,潍县凸起; WF depression,潍坊凹陷; GDS uplift,汞丹山凸起. 蓝色圆点代表主要城市: CY,昌邑; WF,潍坊; CL,昌乐; LQ,临朐; AQ,安丘. (b) 研究区台站分布及划分区域图. 黑色三角形代表台站,红色三角形指示图5中的0533台站,蓝色实线划分的A、B、C、D四个区域为主要研究区,红色虚线划分的区域E为讨论部分所用区域.
地震波速度各向异性是研究构造活动、介质变形等动力学过程的重要手段,主要分为方位各向异性和径向各向异性两种类型.方位各向异性主要描述了地震波沿不同方位传播速度不同,径向各向异性则是表现了不同偏振方向的横波在速度上的差异.将介质简化为只有5个独立弹性常数的横向各向同性介质(Transversely isotropic medium,TI),根据对称轴的方向,又分为垂直横向各向同性介质(Vertical transversely isotropic medium,VTI)和水平横向各向同性介质(Horizontal transversely isotropic medium,HTI).当地震波沿着水平方向传播时,在VTI介质中,垂直方向偏振的横波将以速度VSV传播,水平方向偏振的横波将以速度VSH传播,此时有径向各向异性,无方位各向异性; 在HTI介质中,偏振方向相同的横波沿不同方位角的传播速度不同,此时既有方位各向异性也有径向各向异性(彭艳菊等, 2007; Xie et al., 2013).但在大部分实际情况中,地球介质的对称轴既不垂直也不水平,而是倾斜的,称为倾斜横向各向同性介质(Titled transversely isotropic medium,TTI).TTI介质更加复杂,同时表现出径向各向异性和方位各向异性特征.根据Xie等(2015)的研究,传统方法测量到的TTI介质的各向异性强度往往比真实介质的各向异性强度小,需要联合两种各向异性反演才能得到更准确的结果.但是由于资料不足以同时考虑两种各向异性,我们在本研究中仅考虑径向各向异性.
利用Rayleigh波和Love波的频散曲线分别反演SV波和SH波的速度结构,进而得到径向各向异性是一种常用的方法(Shapiro et al., 2004; Huang et al., 2010; Moschetti et al., 2010).赵凯锋(2018)使用有限频背景噪声层析成像和远震面波双平面波层析成像技术,反演得到了东秦岭—大别—苏鲁造山带岩石圈横波速度结构及地壳径向各向异性结构,发现苏鲁造山带上地壳整体为正的径向各向异性,推测可能是由正滑型构造带中的塑性变形亚带引起.Ai等(2020)利用Rayleigh波和Love波频散曲线联合反演的方法,构建了华北克拉通三维地壳径向各向异性模型,他们发现渤海湾盆地中下地壳呈现正径向各向异性,推测是中生代晚期至新生代地壳伸展变形导致.上述研究虽然包含了我们的研究区,但是由于研究尺度较大,台站分布稀疏,对浅层结构的分辨率相对较低.因此,需要更加密集的台阵来探究郯庐断裂带潍坊段上地壳径向各向异性结构.
然而,由于浅地壳介质的复杂性以及短周期噪声源的不均一性等因素,短周期噪声面波的双台频散数据通常提取难度大且质量相对较低.一种比较有效的缓解这一影响的方法是采用子阵列划分方法(Luo et al., 2016; 孙楠等, 2021),虽然降低了空间分辨率,但是提取得到的子阵列平均频散通常较为稳定可靠,且可能提取到高阶面波数据,更好地约束变形结构.鉴于此,我们从划分子阵列的角度出发,基于近期新提出的改进的多分量频率-贝塞尔变换方法(Modified multicomponent frequency-Bessel (J) transform method,MMFJ)(Luo et al., 2022a),利用郯庐断裂带潍坊段短周期密集台阵的背景噪声数据,分别提取子阵列Rayleigh波和Love波基阶及高阶频散曲线,再反演横波速度结构并计算径向各向异性.相比于传统的频率-贝塞尔变换方法(Frequency-Bessel (J) method,FJ)(Wang et al., 2019; Hu et al., 2020),MMFJ方法通过消除频散谱中的“交叉”假频,可以从多分量互相关函数中同时提取Rayleigh波和Love波的相对高质量频散数据.此外,虽然通过联合反演Rayleigh波基阶和高阶频散曲线能够获得更稳定的地下横波速度结构已被证实(Xia et al., 2003; 罗银河等, 2008),但是通过联合反演Rayleigh波和Love波的基阶和高阶频散数据确定径向各向异性结构仍然鲜有报道,这可能与传统方法(例如相移法(Park et al., 1998))中同时提取Rayleigh波和Love波基阶和高阶频散数据存在一定困难有关.
本文中,我们将首先介绍MMFJ方法及反演参数,再结合数值例子介绍联合反演方法的分析过程.然后将该方法应用于潍坊密集台阵数据上,最后得到郯庐断裂带潍坊段四个区域的径向各向异性结构.结合该地区的构造背景,我们进一步探讨了区域内的变形结构特征及其对郯庐断裂带构造演化的指示意义.
1 方法
1.1 改进的多分量频率-贝塞尔变换(MMFJ)法
MMFJ方法是Luo等(2022a)在FJ方法(Wang et al., 2019; Hu et al., 2020)和MFJ(Modified frequency-Bessel (J) transform method)方法(Xi et al., 2021)的基础上新开发出来的一种从九分量互相关函数中提取Rayleigh波和Love波频谱能量,并计算去除空间假频的方法,其主要的表达式如下:
(1)
(2)
(3)
(4)
其中,
(5)
(6)

(7)
1.2 反演算法
本研究中,我们使用的反演方法是BFGS拟牛顿法(Byrd et al., 1995),主要利用DisbaTomo程序包(Pan et al., 2019)来反演横波速度结构.根据前人的研究(Xia et al., 1999; Xia et al., 2003; Pan et al., 2019),Rayleigh波相速度对SV波速度最为敏感,对P波速度和密度的敏感性相对较小.Love波相速度对SH波速度最敏感,与密度也有关系.因此,为了减少反演中的变量,在反演过程中,我们仅反演SV波和SH波速度,P波速度和密度由经验关系求得(Brocher, 2005):
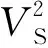
(8)
(9)
对于多阶频散曲线,反演的目标函数如下:
(10)

2 数值模拟
2.1 MMFJ方法在合成数据上的应用
我们首先用一个数值例子来展示MMFJ方法和采取式(7)的应用效果.我们使用一个真实的一维各向同性的六层速度模型作为理论模型(表1; Wang et al., 2019),利用CPS330程序包(Herrmann, 2013)正演三分量连续波形数据,时间长度设为600 s,采样间隔为0.01 s.设置1000个随机震源,震源分布在圆环状空间内,圆环的最小半径为0.5 km,最大半径为1.5 km.50个等间距线性台站位于圆环中央,台站间距为0.0042 km(图2).参考Bensen等(2007)和Zhang等(2018)提出的噪声数据处理流程,我们首先对单台原始数据进行预处理,包括去均值,去趋势,频率谱白化和时间域滑动时窗正则化.计算台站对互相关函数时,我们采取先计算E,N,Z坐标下的互相关函数,再乘以旋转张量旋转到R,T,Z坐标的策略(Lin et al., 2008; Hu et al., 2020), 最终得到R,T,Z坐标下的九分量互相关函数.然后我们分别用FJ方法和MMFJ方法计算Rayleigh波和Love波的频散谱,对比说明MMFJ方法消除频散谱“交叉”假频的效果.结果如图3所示,可以看到,FJ方法得到的频散谱(图3a,3c)上存在明显的“交叉”假频,在MMFJ方法得到的频散谱(图3b,3d)上被有效地消除了,使得频散谱上的频散能量更加清晰,验证了MMFJ方法和采取式(7)计算频散谱的有效性.
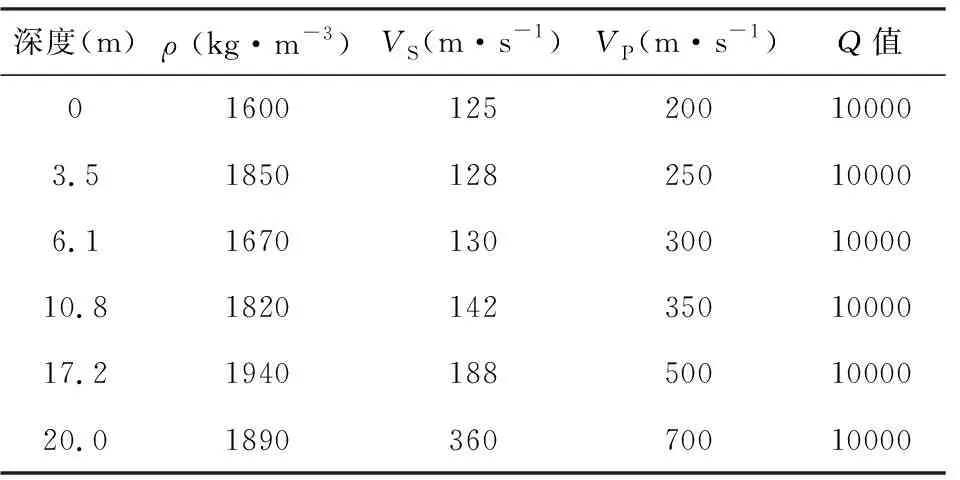
表1 六层速度模型参数表Table 1 Parameters of the six-layer model

图2 数值实验中的噪声源与台站分布(a) 数值例子中的噪声源与台站分布图.图中蓝色的点代表噪声源,黑色三角形代表台站; (b) 50个台站的具体分布图.

图3 数值例子得到的FJ频散谱(a) 多分量FJ法得到的Rayleigh波“求和”谱IRsum; (b) MMFJ方法得到的Rayleigh波“求和”谱 多分量FJ法得到的Love波频散谱IL0; (d) MMFJ方法得到的Love频散谱 图中红色点线代表理论频散曲线,白色点线代表拾取的频散曲线.
2.2 联合反演基阶和高阶面波频散确定径向各向异性

我们将两种反演模型进行对比: 只用基阶频散曲线反演和联合基阶和一阶高阶频散曲线反演,反演结果如图4所示.从图4a—h的结果对比中可以看出,联合反演基阶和一阶高阶Rayleigh波和Love波频散数据相较于单独反演基阶频散数据,能够有效降低反演模型的多解性.图4i展示了反演得到的径向各向异性结构.由于我们使用的理论模型是各向同性模型,所以每一层各向异性的值理论上应为0.可以看到,虽然我们仅联合了一阶高阶频散曲线反演,但相比于只用基阶频散曲线反演,联合反演的结果对二至六层的径向各向异性结构有更好地约束,说明联合高阶频散曲线反演可以提升径向各向异性结构的稳定性.

图4 只用基阶频散反演结果和联合基阶与高阶频散反演结果对比(a)—(d)是只用基阶频散曲线反演的结果以及对应的频散曲线的拟合情况,其中(a)、(b)为Rayleigh波频散及反演模型,(c)、(d)为Love波频散及反演模型; (e)—(h)为联合反演基阶和高阶频散的结果,其中(e)、(f)为Rayleigh波频散及反演模型,(g)、(h)为Love波频散及反演模型. 频散拟合图中,蓝色的点代表反演使用的频散数据,灰色的线代表反演模型正演得到的频散. 模型图中,灰色虚线代表初始模型选取范围,灰色实线代表反演得到的速度模型,红色实线是这些速度模型的加权平均,蓝色实线代表真实的速度模型; (i)为径向各向异性结果. 其中黑色实线为只用基阶频散曲线反演得到的径向各向异性结构,用RA′表示; 红色实线为联合反演得到的径向各向异性结构,用RA表示. 灰色实线为理论径向各向异性结构.

图5 0553台站与其他台站九分量互相关函数示例图. 其中互相关函数的频带为0.5~10 s

图6 MMFJ法应用到潍坊台阵数据得到的区域A—D对应的频散谱(a)、(c)、(e)、(g)表示A、B、C、D四个区域的Rayleigh波“求和”谱表示A、B、C、D四个区域的Love波频散谱 红色点线是根据靳佳琪等(2023)得到的区域SV波平均速度模型正演的理论频散曲线,白色点线代表拾取的频散曲线.
3 郯庐断裂带潍坊段密集台阵数据及应用
3.1 数据处理
我们再将MMFJ方法和联合反演方法应用至潍坊台阵实际数据.我们使用的数据是中国地震局物探中心在潍坊附近布设的302个短周期台站的背景噪声数据.采集地震数据的仪器是自然周期为5 s的三分量EPS地震仪,采样频率为200 Hz.采集时间段为2017年8月1日至10月31日,共计3个月.台阵走向与断裂带走向基本平行,东西方向排列20个台站,南北方向排列15个台站,台间距约5 km.台站分布如图1b所示.
我们首先对单台原始数据进行预处理,先将数据重采样到10 Hz,其余步骤与2.1节预处理流程相同,再计算九分量互相关函数.如图5所示,为台阵中的0533台站与其他台站的九分量互相关函数示例,可以看到,ZZ、ZR、RZ、RR、TT互相关分量中都出现了明显的面波信号.RT、TR、TZ、ZT互相关分量中出现较弱的面波信号,这可能与仪器布设指北存在偏差以及地下非均匀介质导致的复杂波场有关.
我们进一步应用MMFJ方法至潍坊台阵多分量互相关数据上.结合潍坊密集台阵的展布和主要地质单元的分布特性,我们将研究区分成了若干子阵列.利用MMFJ方法分别获得每个子区域的Rayleigh波和Love波频散谱.根据频散谱的实际质量,我们最终选择了潍坊段东侧和南侧A、B、C、D四个子区域(图1b中蓝色框线所示)计算频散谱并反演横波速度结构.如图6所示,是这四个区域的Rayleigh波和Love波频散谱.四个区域的Love波频散谱上都可以看到明显的基阶及一阶高阶信号(图6b,6d,6f和6h),其中区域A的Love波频散还出现了二阶高阶信号(图6b).但是四个区域的Rayleigh波高阶频散能量都没有Love波明显,只出现了微弱的一阶高阶信号.除此之外,我们还可以看到图6的频散图像中,均出现了“放射状”假频,根据Cheng等(2023)的研究,我们认为这种能量较强且与真实频散相交的“放射状”假频主要是空间采样率不足导致,由于本研究使用的MMFJ方法消除的是“交叉”假频,我们在本研究中没有涉及对“放射状”假频的消除.
3.2 郯庐断裂带潍坊段上地壳径向各向异性结构
基于2.2节的联合反演方法,我们应用至潍坊台阵的四个子阵列的频散数据上.由于部分区域频散谱受到“放射状”假频或者其他信号的影响,高阶频散曲线的能量相对粗糙(比如图6b,6d), 为了保证拾取到的频散曲线尽量可靠,我们采用手动拾取的方式拾取Rayleigh波和Love波的频散曲线.手动拾取可以从主观上舍弃一些波动较大、或者受“放射状”假频影响的能量,同时我们在拾取的过程中也尽量保证拾取的点之间的频率间隔不会相差太大.然后我们以靳佳琪等(2023)所得的潍坊段上地壳SV波速度模型进行平均作为参考模型,分层结构与靳佳琪等(2023)的模型保持一致,即 0~1.2 km深度每0.2 km一层,1.2~1.5 km深度每0.3 km一层,1.5~3 km深度每0.5 km一层,3~6 km深度每1 km一层,6~7.5 km深度每1.5 km一层.为了控制深部速度结构对反演的影响,我们将Luo等(2022b)所得的的郯庐断裂带中南段0~300 km 深度的SV波速度模型进行一维平均和近似,拼接至靳佳琪等(2023)的模型上,以此拼接模型作为我们初始模型.模型中的P波速度和密度由经验公式基于SV波速度算出(式(8)和式(9)).我们根据参考模型随机生成了40个初始模型,模型的波动范围为±0.4 km·s-1,然后分别反演A、B、C、D四个区域的SV波和SH波速度结构,再将这40个反演模型结果加权平均作为最终速度模型.图7为A、B、C、D四个区域Rayleigh波和Love波反演情况.可以看到,A、B两个区域相邻,速度结构也相近,浅层2 km以上的SV波速度和SH波速度相较于C、D区域偏低.C、D两个区域虽然相邻,但是区域C浅层2 km以上的SV波和SH波速度相对于区域D均明显偏低.这可能是因为区域C和区域D所在的地质单元不同,区域C主要经过胶莱盆地,浅层以沉积层为主,区域D主要位于胶北隆起内,浅层以元古宙地层和中生代岩体为主(张鹏等, 2010; 李洪奎等, 2017; 张尚坤等, 2021),所以导致了区域D浅层横波速度较区域C偏高.
然后我们再利用四个区域的SV波和SH波速度模型,分别计算径向异性结构,结果如图8所示.可以看到,区域A的径向各向异性结构较复杂,浅层0~2 km为负,2~6 km经历了由正到负的转折,6 km以下又为正值.这可能是由于区域A垂直于郯庐断裂带构造方向,不仅包含鲁西隆起、汞丹山凸起等构造单元,还横跨郯庐断裂带四条主断裂、李家庄断裂和景芝断裂,高速和低速区交错相连,区域平均结构比较复杂,所以径向各向异性出现了两次转折.区域B径向各向异性在0~4 km为负,4~7.5 km为正,径向各向异性的强度与区域A类似.区域C浅层径向各向异性值较小,且200 m以浅为正值,然后逐渐反向增大转变为负值,直到3 km之后又转为正值.区域D浅层0~1 km径向各向异性为负,且随着深度的增大逐渐减小,到2 km处转变为较小的正值,然后转变为负值,直到5 km处又转为正值.我们认为,虽然区域C和区域D相邻,但可能是由于两个区域跨过的地质单元不同,导致浅层的径向各向异性差别较大.区域C主要位于胶莱盆地内,浅层以松软沉积为主,导致速度偏小、径向各向异性值最浅层为正.区域D浅层1 km以上速度和径向各向异性值均相对偏大,可能是由于区域D主要位于胶北隆起内,浅层以元古宙地层和中生代岩体为主(张鹏等, 2010; 李洪奎等, 2017; 张尚坤等, 2021),更容易产生垂直裂隙,导致径向各向异性为负.虽然四个区域的径向各向异性局部结构相对复杂,但是我们发现,从整体的趋势来看,四个区域均在约2 km以上,径向各向异性为负(VSH
4 讨论
我们利用郯庐断裂带潍坊段的密集台阵数据,基于近期提出的MMFJ方法,提取到了四个子阵列区域的Rayleigh波和Love波基阶和高阶频散数据,并且通过联合反演Rayleigh波和Love波基阶和高阶频散数据,得到了四个子区域内的浅地壳径向各向异性结构,为区域介质变形结构的演化过程提供了一定的约束.本研究所采用的MMFJ方法是在传统FJ方法的基础上,进一步计算了多分量频散谱,还消除了频散谱上的“交叉”假频,一定程度上提升了频散提取的准确性.但是在应用这种阵列频散提取方法的过程中,我们发现当子阵列位于松软沉积层或者子阵列展布范围过小时都会影响到频散谱的质量.因此,在接下来的讨论中,我们将从沉积层对面波频散谱的影响、台阵展布对面波频散谱的影响以及郯庐断裂带上地壳变形结构等三个方面展开.
4.1 沉积层对FJ频散谱的影响
前面的章节中我们主要用潍坊台阵的南侧和东侧数据进行研究,没有涉及到台阵西北侧区域.这主要是因为在西北侧区域(图1b红色虚线框所示区域E)采用MMFJ方法所提取出的频散谱能量相对较弱.如图9a—b所示,分别对应从区域E提取的Rayleigh波和Love波频散谱.从图中可以看到,频散谱的基阶频散能量有效频带较窄(0.1~0.3 Hz),且一阶高阶的能量也相对分散,不利于频散曲线的提取与反演.根据前人反演的速度模型(Ma et al., 2020; 靳佳琪等, 2023),我们推测导致区域E频散谱质量相对较弱和发散的原因可能有以下两方面: 第一,区域E浅层主要以第四纪松软的沉积层为主(张鹏等, 2010; 李洪奎等, 2017; 张尚坤等, 2021),且低速层可以持续到5 km附近.松软的低速层使信号高频能量衰减更快,导致频散谱中几乎没有高频面波信号出现.第二,区域E位于横向速度变化剧烈的区域,凹陷构造与凸起构造交错,这种强烈的速度差异也可能导致台阵频散谱面波能量变弱且发散(吴高雄, 2020; 孙楠, 2021).
4.2 台阵展布对FJ频散能量的影响
我们在实践中发现,不同的台阵展布对所提取到的频散数据质量也存在一定的影响.Wang等(2019)、Cheng等(2023)的研究中也指出,频散谱的分辨率与所选区域的台阵展布有关,展布越大,分辨率越高,同时台阵展布还限制了频散谱上能够分辨的最低和最高频率.我们利用潍坊段实际数据进行了一个测试.如图10a所示,我们在断裂带东支东侧选取了四个逐渐扩大的区域,分别用黑、黄、红、蓝四种颜色表示.根据靳佳琪等(2023)反演的速度模型,我们可以知道这四个区域速度结构基本一致,理论上频散曲线也不会有太大差别.我们用MMFJ方法分别提取这四个区域的Rayleigh波和Love波频散,并手动拾取基阶频散曲线进行对比,如图10b和10c所示.可以看到,黑框和黄框区域由于台阵展布过小,Rayleigh波和Love波频散曲线在低频区域(灰色阴影所示)出现了异常偏高以及不稳定的现象,这将对反演速度结构造成较大误差.随着选取区域逐渐扩大,红框和蓝框区域对应的频散曲线在低频段才逐渐趋于稳定.因此,为了保证反演结果的可靠性,我们没有采取传统的移动小阵列的方式获取更精细的三维结构.
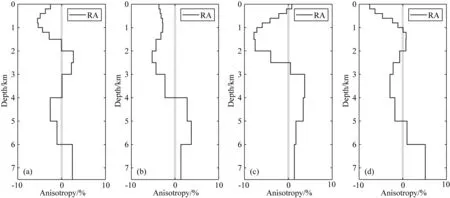
图8 A、B、C、D四个区域的径向各向异性结果,用RA表示

图9 MMFJ法应用到区域E对应的频散谱(a) 区域E对应的Rayleigh波“求和”谱 区域E对应的Love波频散谱 红色点线是根据靳佳琪等(2023)得到的区域SV波平均速度模型正演的理论频散曲线.
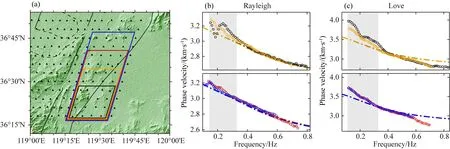
图10 台阵展布对FJ频散数据影响测试结果(a) 逐渐扩大的四个区域,分别用黑、黄、红、蓝色框线表示; (b) 四个区域Rayleigh波基阶频散曲线,频散曲线颜色同区域框线颜色; (c) 四个区域Love波基阶频散曲线,频散曲线颜色同区域框线颜色. 对应颜色的虚线是根据靳佳琪等(2023)得到的区域SV波平均速度模型正演的理论频散曲线.
4.3 郯庐断裂带潍坊段上地壳变形结构
地震各向异性是地球介质的一个重要特征,指示了区域的演化与构造过程.相比于上地幔各向异性,地壳中的各向异性的成因往往比较复杂: 对于上地壳径向各向异性,一般认为是由于微裂隙的定向排列导致,而微裂隙的排列方向主要与岩层的变形节理以及应力场有关(Crampin and Chastin, 2003); 对于中下地壳各向异性,通常认为来源于岩石矿物中的晶格优选方位(lattice-preferred orientation, LPO)(Mainprice, 2007).
从本文的反演结果上来看,A、B、C、D四个区域整体都有一个相同的趋势,即约2 km以上径向各向异性为负,5 km以下径向各向异性为正,具有“浅负深正”的特征.靳佳琪等(2023)的结果也显示出该区域4 km附近的速度结构和方位各向异性特征均有明显的变化.因此,我们推测该区域3~4 km附近可能是一个构造分界面,指示了不同时期的构造变形状态.我们用一个卡通图(图11)来说明该区域的主要变形机制.0~2 km,该区域主要呈现负的径向各向异性特征,根据前人在沂沭断裂带附近的地震剖面与地质调查结果(严乐佳等, 2014; 徐盛林等, 2016; 张尚坤等, 2021),该区域四条主干断裂F1,F2,F3,F4均为倾角较大且局部近直立的中生代断裂,在这些主断裂的控制下,沿着主断裂发育有一系列次生断裂,这些断裂一部分与主断裂同属于中生代伸展断裂系,受到郯庐断裂带早期走滑、拉张的作用,断裂面近直立并平行于主断裂; 另一部分是在新生代构造过程中,以中生代断裂为基础,沿着这些深大断裂发生伸展变形,形成现今的浅部正断裂系.这些断裂的构造面在浅部多数倾角较陡(张尚坤等, 2021),具有大量的垂直分量(Xie et al., 2013),可能就是导致研究区浅层呈现负径向各向异性的原因.研究区5 km以下主要呈现正径向各向异性,我们认为可能是由于早白垩世以来太平洋板块向西高角度俯冲后撤,郯庐断裂带表现为伸展活动(Zhu et al., 2010),在这种伸展沉积环境下形成的水平结构主要表现出正径向各向异性的特征.而2~5 km之间,四个区域径向各向异性结构各有不同,总体处于由负到正的转折状态.我们推测可能不仅受控于2 km以浅的近垂直断裂系,也受到5 km以深的水平沉积结构的影响,导致径向各向异性结构较为复杂.
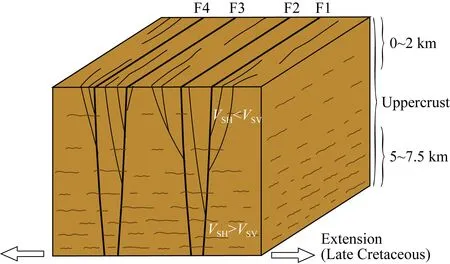
图11 郯庐断裂带潍坊段可能的变形机制卡通图
5 结论
本研究利用郯庐断裂带潍坊段密集台阵数据,基于改进的多分量频率-贝塞尔变换(MMFJ)法,提取得到了郯庐断裂带潍坊段四个子阵列Rayleigh波和Love波基阶及高阶频散曲线,并且联合反演得到了郯庐断裂带潍坊段四个区域内的径向各向异性结构.数值实验结果表明,采用联合反演Rayleigh和Love波的基阶和高阶模式频散能够有效降低径向各向异性结构的多解性.郯庐断裂带潍坊段的实例结果表明,四个区域内的径向各向异性结构揭示潍坊段径向异性整体呈现“浅负深正”的特征,即郯庐断裂带潍坊段东侧和南侧在约2 km深度以浅,径向各向异性为负,这种变形特征可能主要受控于潍坊段的垂向断裂体系; 在5 km以深,径向各向异性为正,这可能与白垩世以来郯庐断裂带的伸展活动有关.2~5 km之间,四个区域径向各向异性结构各不相同,总体处于由负到正的转折状态.我们推测可能不仅受控于2 km以浅的近垂直断裂系,也受到5 km以深的水平沉积结构的影响.我们的研究也发现,采用子阵列提取频散的方式可能受到沉积层结构以及阵列展布的影响,这也为今后类似研究提供参考.
致谢感谢中国地震局地球物理勘探中心为本研究提供了台阵波形数据,感谢两位审稿人和编委对论文提出的宝贵修改意见.

