海底震后形变多基站联合估计模型

薛树强, 肖圳,*, 董杰, 韩保民, 孙悦,, 杨文龙

1 中国测绘科学研究院地理信息工程国家重点实验室, 北京 100830

2 山东理工大学建筑工程与空间信息学院, 山东淄博 255049

0 引言

随着以全球导航卫星系统(Global Navigation Satellite System, GNSS)为代表的空间大地测量观测技术的发展和成熟,大地测量监测网络已实现全球陆域有效覆盖,且实现了长期连续观测(杨元喜等,2011,2020).然而,占地球表面积71%的海洋还存在大量海底基准空白和导航定位服务盲区(杨元喜等,2017).为此,国际大地测量协会专门成立了海洋大地测量交叉委员会(Poutanen and Rózsa,2020);同时,我国在“十三五”期间也开展了海底大地测量基准试验网建设(中国科学院,2022).新一代大地测量观测系统(Global Geodetic Observing System, GGOS)致力于地球变化监测并为地震等灾害过程研究提供高精度观测,但由于绝大部分地震发生在板块交接带,且分布于海底(Bürgmann and Chadwell,2014),导致海底构造探测和地震等灾害过程研究在广阔海域缺少有效约束(Liu等,2023).因此,海底大地测量对于全球海底板块监测、地球动力学和地震等灾害过程研究具有重要意义.

最近20多年来,震后形变理论和算法得到了较大的发展(Sun and Okubo,1993;乔学军等,2021;刘泰等,2022),国内外许多学者基于大地测量观测对震后形变开展了大量研究工作,例如有学者利用震后黏弹性模型研究地震后对周边区域地壳形变的影响(余建胜等,2018;刘泰等,2017;陈飞等,2020);还有学者从Sentinel-1和ALOS-2图像中获得同震形变场并进行一系列分析(姜卫平等,2022);也有学者利用水准监测数据建模推断震后形变源和震后形变机制(Hao et al.,2012;Iinuma et al.,2012);Tobita结合日本东北部GNSS时间序列和指数、对数模型构建了震后形变模型(Tobita,2016).在GNSS坐标时间序列震后形变估计方面,不少学者研究采用分步估计法,即先利用震前数据估计站速度,然后通过去除震后数据中站速度引起的位移和同震形变得到震后形变(Gonzalez-Ortega et al.,2014;Tobita,2016).对GNSS时间序列进行整体建模的模型参数估计具有更为严密的理论基础(Altamimi et al.,2016).此外,GNSS测站震后形变具有相同的驱动机制,所以相近测站具有相似的震后形变,从而导致GNSS时间序列中存在共模形变,因此已有学者采用主成分分析法(Principal component analysis, PCA)提取共模形变,且采用两步法估计或迭代估计得到更为合理的震后形变参数(Savage and Svarc,1997;苏利娜等,2019).

利用海底大地测量开展地震过程研究,已成为最近十多年来的热点研究课题(Fujiwara et al.,2022;Iinuma et al.,2012;Ozawa et al.,2012;Watanabe et al.,2014;孙悦等,2023).目前,海底大地测量、海底板块运动和扩张监测等通常基于全球导航卫星系统-声学(Global Navigation Satellite System-Acoustics, GNSS-A)组合观测方法实现,该方法最早由美国斯克利普斯海洋学研究所提出(Spiess,1980).水下定位受复杂海洋温度、盐度等环境参数影响,特别是海洋声速场随时间和空间都存在显著的差异性,给水下精密定位带来了极大挑战(赵建虎和梁文彪,2019;薛树强等,2023).为了提高水下定位精度和可靠性,通常需要在等水深的半径上均匀布设多个海底基准站构成区域海底基准网(Yokota et al.,2016;Matsumoto and Fujita,2008),例如,美国学者提出的在海底布设3～4个海底基准站的方法一直被日本等沿用至今(Spiess,1985a,1985b).该方法经过最近20多年的发展和完善,其平面定位精度已经达到2～3 cm(Fujita et al.,2006;Watanabe et al.,2020;Yang and Qin,2021),而Sato等利用日本东北大地震前的数据对日本海底地壳运动观测系统进行了评估,结果表明,海底基准站高程定位精度也可达到10 cm(Sato et al.,2013b).海底基准站观测设备由于供电等问题需要新旧站更替或替换电池,由于水下作业的固有成本和技术难度,通常采用新旧站更替方式保证时间序列的连续性,且每年一般只能复测3～5次,导致海底基准站坐标时序样本相对较小,无法与GNSS等实时连续大地测量观测相比(Yokota et al.,2018).除上述原因之外,水下定位还会受到测量船相对于海底控制点的航迹、声速剖面误差的影响(马越原等,2022;肖圳等,2023;Xue et al., 2023).

日本近20年建立了世界上最为密集的海底地壳运动观测网络(Ozawa et al.,2002;Ozawa et al.,2012;Yokota et al.,2016),该网络清晰记录了一些大型地震引起的形变等,许多学者在此基础上对2011年日本东北部地震(MW9.0)进行了研究,例如,有学者实现了灾害过程模拟(Iinuma et al.,2012; Sun et al.,2014),研究了日本东北部地震导致的同震滑动分布和板块间耦合(Iinuma et al.,2012;Sato et al.,2013a).日本学者利用海底大地测量也开展了大量地震过程研究,并在2020年公开了7个海底站的十年尺度监测资料,这为本文研究提供了数据条件.本文借鉴国际地球参考框架2020(ITRF 2020)震后形变研究思想(Altamimi et al.,2016),结合海底基准站坐标时序样本小、存在中断等实际问题,构建了以站速度和震后形变作为公共参数的多站联合时序分析模型;后又提出了将N-E方向震后形变弛豫因子作为公共参数的震后形变参数联合估计模型,并提出了求解站坐标、站速率等线性参数和震后形变非线性参数混合模型的“一步法”;最后采用日本海底基准站网观测时序验证了本文的主要研究结果.

1 海底震后形变模型

海底震后形变会影响海底基准站坐标时序分析,对海底基准维持产生不利影响.为此,本文尝试引入海底基准参考历元,并构建海底基准站坐标、速度、震后形变等数联合估计模型.由于海底基准站局部网通常布设在地壳构造稳定区域,且分布以水深为半径的圆上,可假设有K个海底基站,第i个海底基站在参考历元t0时刻的平面坐标为xi0(i=1,2,…,K),所有海底基准站具有相同的速度v0和相同的震后形变,则t时刻的海底基准站网坐标可表示为

(1)

其中,v0称为海底基准站在参考历元t0的速度,δPSD为震后形变,εi(t)为观测误差.上述模型将邻近站点的海底震后形变作为公共参数,因此我们称其为海底震后形变网解模型.考虑海底基准站定位精度相对较低,且海底复测周期长导致观测样本有限,所以本文建议采用上述多站联合的网解模型.相对于GNSS测站相距几十千米,海底基准站间相距仅有几百米到几千米,故而将站速度和震后形变参数作为公共参数是合理的.相比于基于主成分分析方法的震后共模形变提取方法(苏利娜等,2019),本文认为上述公共参数法对于平滑观测噪声可具有更强的约束性.

海底基准站随板块存在近似线性运动的同时,还会受地震等地质事件影响,存在非线性运动.震后形变通常采用指数或对数函数模拟,如指数函数模型可表示为(Altamimi et al.,2016,2018)

(2)

其中,y=[KEKNτ]T,KE,KN分别为E方向和N方向的振幅因子,τ分别为震后形变弛豫因子(我们假设N方向和E方向具有相同的弛豫因子),T0为地震发生时刻.已有学者利用指数和对数组合模型开展震后形变分析,并给出了相应参数的物理意义(Tobita,2016).在实践中,分别对测站坐标时序分量构建震后形变模型,会得到不同的弛豫时间因子.然而,对于同一个地震事件,不同方向的震后弛豫因子应该是相同的.因此,本文采用N-E时序联合估计地震形变弛豫时间因子.需要指出,虽然理论上地震会影响全球测站坐标时序,但无论是从计算成本还是从实际应用方便角度,对震后形变参数实施假设检验,当震后形变参数显著时方可视为模型误差予以参数化估计,即上述模型应建立在震后形变识别基础上.当采用假设检验方法对附加参数进行识别时,需要充分考虑检验参数的相关性问题.对于长时序分析问题,参数间的相关性一般很低,此时建议采用t检验对对逐个参数施加假设检验(陶本藻,1986).此外,对于多维模型参数选取问题,亦可采用更为高效的AIC或BIC信息熵准则(Akaike,1973;薛树强和杨元喜,2013;薛树强等,2022).

当存在n个观测历元时,可构建观测方程：

j=1,2,…,n

(3)

其中,xij=xi(tj)为海底基准站在观测历元tj的坐标,可由GNSS-A观测技术获取.上述多站联合网解模型及N-E时序联合估计模型,也是解决目前海底基准站小样本坐标时序观测和观测精度相对较低问题的有效途径.

2 海底基准站坐标与速度联合估计模型

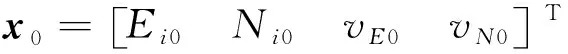
Eij=Ei0+vE0(tj-t0)+δEPSD(tj)+εEij,Nij=Ni0+vN0(tj-t0)+δNPSD(tj)+εNij,

(4)

线性化可得

dLi,j=ai,jdxi+bi,jdy,

(5)

其中,dxi=[dEidNidvEdvN]T,dy=[dKEdKNdτ]T,

(6)

(7)

(8)

当存在K个海底基准站和n个观测历元时,即可构成如下矩阵形式的观测模型：

dL=CdX+ε,

(9)

(10)

其中,

(11)

为K个测站在n个观测历元的累计设计矩阵.考虑当非线性迭代广泛存在的不适定问题,建议考虑附加一定先验约束.

基于高斯-牛顿法可迭代计算线性化观测模型(9)的非线性最小二乘解,即

(12)

w(dLi)=

(13)

为等价权因子,σ0为观测单位权方差.IGGIII方案拥有正常权段、可疑降权段、以及淘汰权段,可以充分利用观测数据,具有较强的抗差性,其中,k1=1.5,k2=2.5为常用推荐值(杨元喜,1996).

采用类似的方法,可以分别获取E方向和N方向的震后形变振幅和弛豫时间因子,下文不再赘述.此外,拟合震后形变模型也可采用以下“两步法”,即

(1)首先,忽略模型(5)中的震后形变项,获取观测时序残差V,即

V=[I-A(ATPA)ATP]dL;

(14)

(2)将上述残差向量作为虚拟观测量,采用高斯-牛顿法求解震后形变参数,即

(15)

其中,dSk=V-δPSD(y,t),δPSD(y,t)为全部观测的非线性函数模型项.

需要指出,上述两步法需要考虑残差之间的相关性,并需要迭代计算以消除分步估计的影响.对于小样本观测,忽略残差的相关性可能会对震后形变参数估计产生较大影响.考虑到海底基准站一般每年复测3～5次,观测样本较小会导致残差相关性较大,本文建议采用理论更为严密的“一步法”,即采用模型(12)一次获取站坐标及震后形变参数.

3 试验结果分析

2011年3月11日,日本海底发生了9.0级大地震,国内外学者围绕日本震后地球物理反演开展了大量研究工作(Ozawa et al.,2012;Sun et al.,2014;陈飞等,2020).本文利用日本公布的7个观测站在2011—2020年的GNSS-A实测数据(空间分布如图1所示)验证本文方法的有效性.这7个站均受到2011年日本大地震的影响,以FUKU站为例,E方向的中心点站坐标时序如图2所示,可以看到在2011年3月日本大地震发生后坐标受到地震影响,随着时间的推移逐渐恢复线性趋势.

图1 日本海底基准站分布

图2 受震后影响的FUKU站中心点坐标时序

使用本文提出的海底震后形变网解模型以及两步法分别对日本公开的7个测站坐标时序求解各测站的站速度和震后形变等参数,水平方向的震后形变参数 (振幅、弛豫因子)如表1所示.

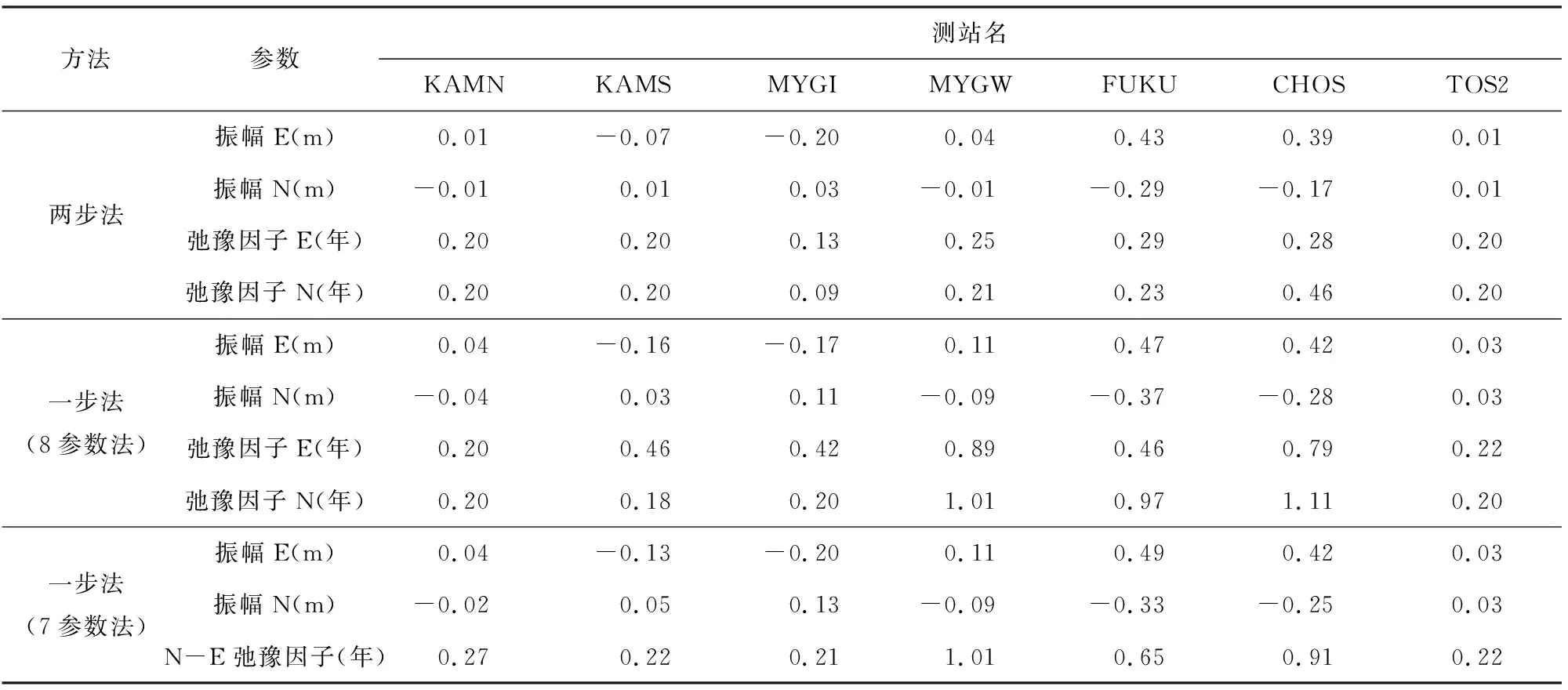
表1 两步法结果与本文模型解对比Table 1 Comparison between two-step method and the proposed model solution

由于弛豫因子主要与地壳黏滞系数和弹性厚度有关,结合区域构造特征可知(见表1),KAMN、KAMS、MYGI三个站所在块体具有相同运动趋势,而MYGW、FUKU、CHOS三个站又与上述三个站具有反向运动趋势,而TOS2距离震中较远,又表现出于上述三个站不同的运动趋势,然而,两步法得到的震后弛豫因子多数均在0.2年左右,他们之间的区分度很小,这意味着利用小样本时序残差震后形变参数容易低估弛豫因子的数值.相比之下,一步法得到的弛豫因子结果区分度较好.另外,因为不同海底基准站相对于地震发生时刻的复测时间不同,所以基于不同海底基准站坐标时序分析得到的震后形变振幅和弛豫因子并不在统一的时间参考下.为此,我们统计了日本海底基准站相对于地震发生时刻的复测时间信息,如图3所示.

图3给出的7个海底基准站复测时间分布图表明,TOS2站捕获的地震形变弛豫因子会相对较小,其他站也会存在微小差异,我们称之为弛豫因子偏差.为此,我们将计算得到弛豫因子偏差(如表2所示)补偿到各测站时序提取的弛豫因子上,得到统一到地震发生起始时刻的震后形变弛豫因子.

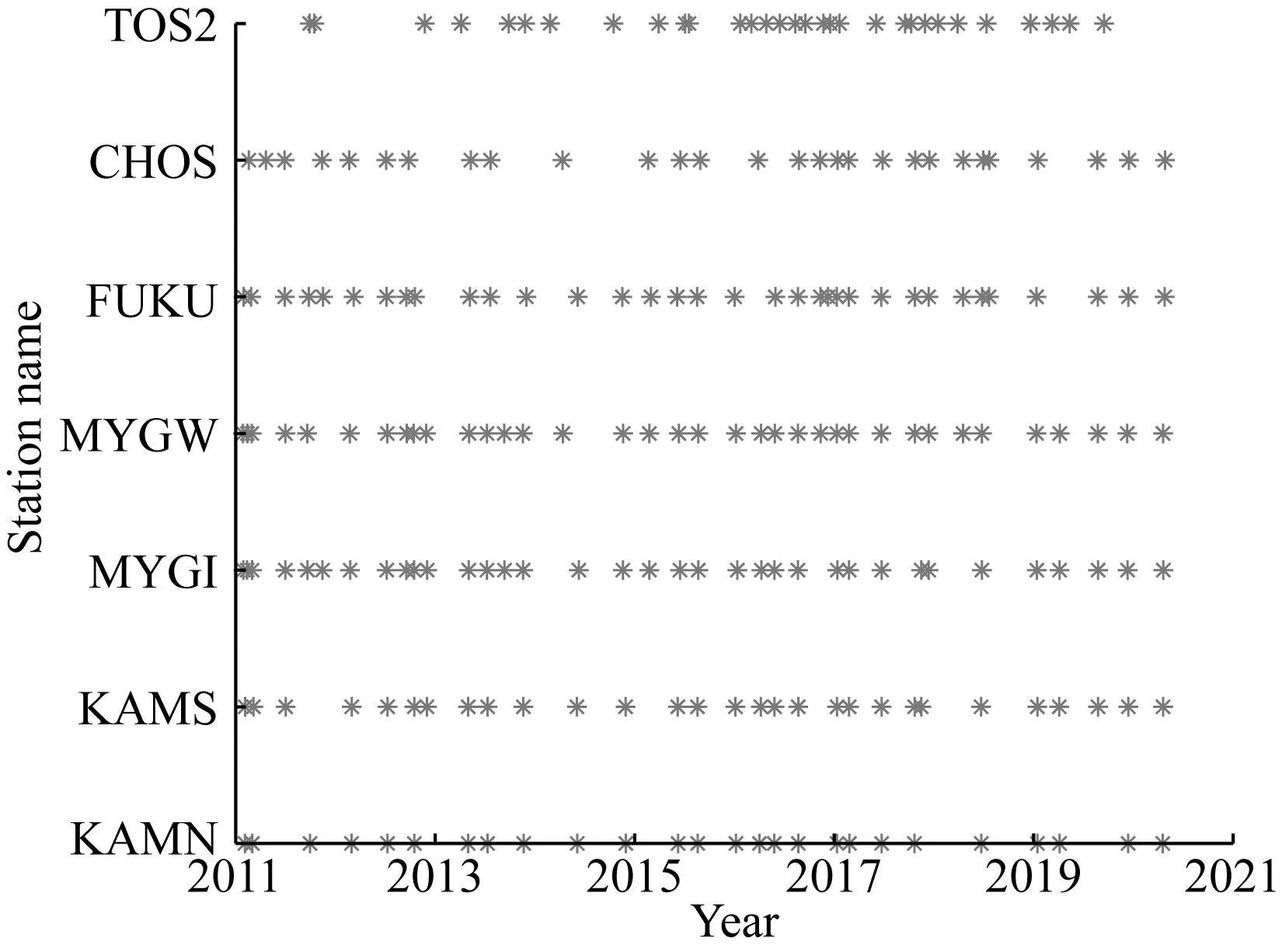
图3 7个海底基准站复测时间分布

表2 各测站弛豫因子偏差Table 2 Relaxation factor deviation of each station

将各测站弛豫因子偏差补偿到计算出来的弛豫因子参数后的两步法与海底震后形变网解模型一步法(分为联合估计N-E方向弛豫因子和分别估计N、E方向弛豫因子)结果对比如表3所示.

表3 补偿后两步法与海底震后形变网解模型参数结果对比Table 3 Comparison of model parameters between compensated two-step method and post earthquake deformation network

由表3可知,两步法得到的弛豫因子依然没有较好的区分度.需要指出,对于GNSS基准站连续坐标时序的大样本情形,残差的相关性可以忽略,但上述试验结果表明,对于海底基准站复测小样本观测情形,残差的相关性可对震后形变估计产生很大影响.一步法(7参数法)即N-E联合估计得到的弛豫因子明显可以根据数据的大小分为两组(前三个站为一组,后四个站为一组),这主要是因为,两组观测站空间分布差异性决定的,即处于两个不同的块体上,这一结论与实际站速度观测整体也是基本符合的(如图4),因此本文认为研究海底震后形变参数时使用一步法(7参数法)得到的结果相比于两步法要更准确.

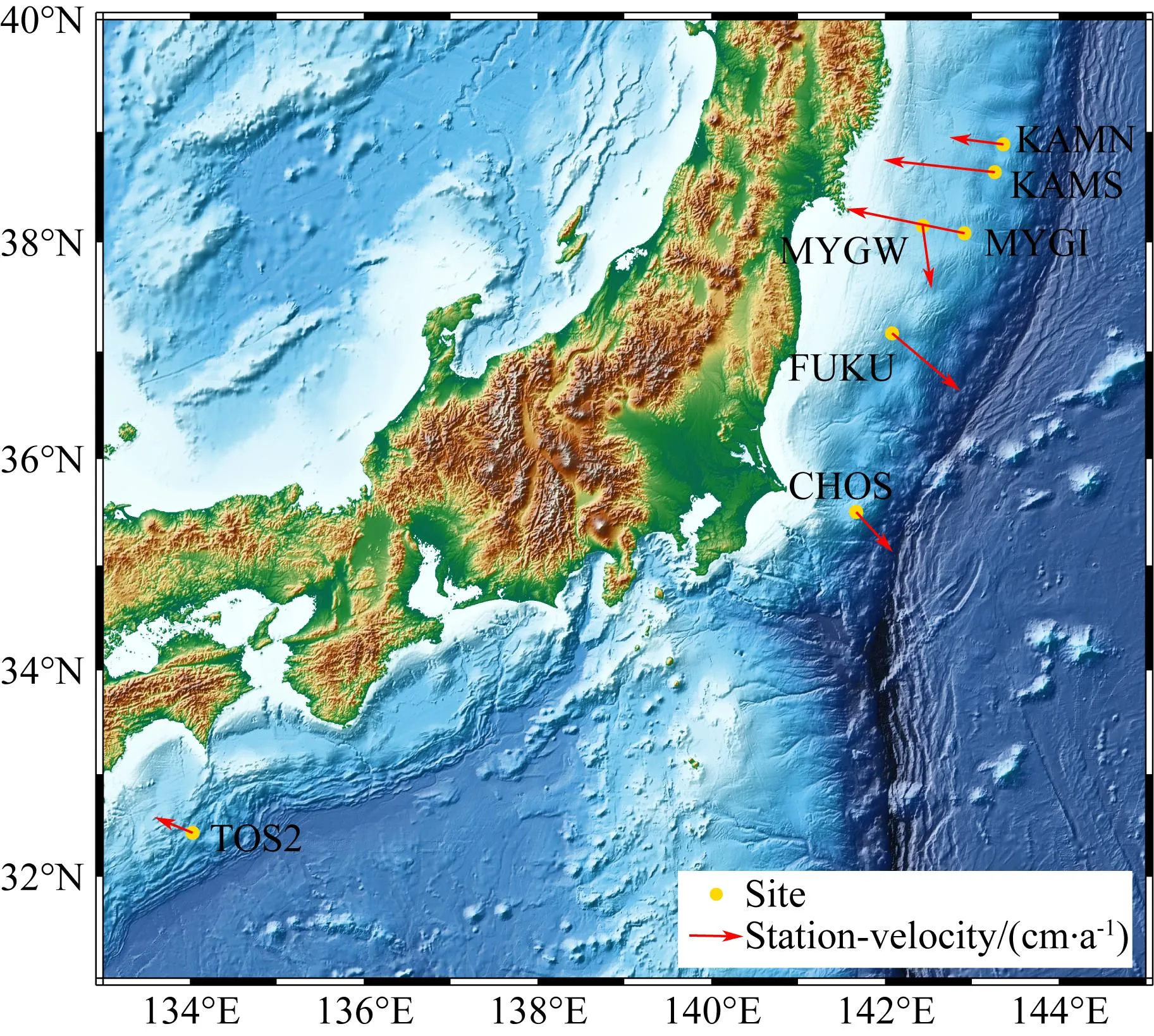
图4 海底基准站运动

4 结论

对海底局域网内的多个基准站坐标时序联合处理,不仅可以提高海底板块运动的监测精度,也可以提高海底震后形变信息提取的敏感性.受限于观测成本和观测技术所限,一般每年只能对海底基准开展3～5次复测,相对GNSS而言其复测精度也偏低,为此,本文建议将多个测站的站速度和震后形变参数作为公共参数处理,并采用“一步法”对线性参数和非线性参数进行联合解算.利用海底基准站复测坐标时序研究震后弛豫因子时,需要充分考虑地震发生时刻与海底基准站复测时刻的偏差影响.

当采用“两步法”提取震后形变信息时,受海底基准坐标观测时序的样本大小限制,必然导致其在第一步时间序列线性拟合阶段获取的残差时间序列存在较大的相关性,若忽略这种相关性影响,则会影响其在第二步提取震后形变信息.因此,本文建议采用“一步法”同时对测站坐标、速度和震后形变参数做出联合估计.我们认为,地震引起地壳形变的弛豫时间不应因坐标系的定义不同而不同,因此,为了更进一步提高震后形变信息提取的可靠性,我们建议将N、E坐标时序中的震后形变弛豫因子作为公共参数进行估计.

研究发现,日本2011年发生了MW9.0大地震后,位于不同海底板块上的海底测站感应到的海底震后形变振幅和弛豫时间存在较为明显的差异性,同一板块上的震后弛豫时间具有较好的一致性,但当采用“两步法”提取震后弛豫因子时,则很难获取与之一致的分析结果.因此本文认为,研究海底震后形变参数时选择一步法会得到比“两步法”更准确的结果.