基于多波长近红外光谱的血红蛋白浓度无创检测技术研究*

彭福来,陈财,张宁玲,王星维,吕丹阳,王卫东

(1.山东中科先进技术有限公司,济南 250000;2.中国人民解放军总医院 医疗器械研发与临床评价中心,北京 100853)

0 引言

血红蛋白浓度检测是临床中常规的检测项目,血红蛋白浓度水平的高低可作为贫血筛查、临床输血指导[1-2]等的重要依据。传统的血红蛋白浓度检测方法需要医护人员对患者取血采样,然后检测样本,该方法具有较高的检测精度,然而由于是有创检测,往往会给患者造成生理和心理负担,且易造成感染;此外,有创检测方法无法连续动态地监测患者血红蛋白浓度的变化趋势,不能及时为术中输血提供指标参考。因此,研究并开发血红蛋白浓度的无创检测技术对疾病筛查、临床输血指导具有重要意义。

近些年,国内外学者相继进行了大量研究来实现血红蛋白浓度的无创检测,研究方法可分为以下几类:第一类是基于光电容积脉搏波描记法(photoplethysmography, PPG)的检测方法[3-7],该方法采用近红外光作为检测光源,光子照射入人体组织后,动脉血液对光子的吸收程度会随心脏的跳动呈周期性变化,因此,出射光的强度也会呈现周期性变化。通过对出射光进行检测,可检测到随心脏搏动的光强度信号,即PPG信号。由于血红蛋白对近红外具有吸收作用,因此,PPG信号含有大量的血液成分信息,通过对该信号进行处理分析,可获取血红蛋白浓度信息;第二类是光谱成像法[8-11],该方法采用白光、近红外等光源照射组织,并对组织进行成像,通过对采集的图像进行处理,可以建立图像与血红蛋白浓度的映射关系,实现血红蛋白的浓度检测;第三类是光声光谱法[12],该方法利用近红外激光脉冲对人体组织照射,血红蛋白对光能量的吸收产生局部热膨胀,该局部热膨胀会产生机械压力,并以声波的形式向周围扩散。通过对该声波进行检测、处理,可以建立声波与血红蛋白浓度的映射关系,实现血红蛋白的浓度检测。

基于PPG的检测方法由于精度较高、可实现性强、成本低等,已成为目前主流的检测方法。

为进一步提高无创检测血红蛋白浓度的准确率,本研究提出了一种基于多波长近红外光的无创检测方法。首先基于Beer-Lambert定律建立了多种不同光谱下的血红蛋白浓度检测模型,并设计了八波长近红外光PPG信号采集系统,对不同波长的PPG信号进行特征提取与选择,构建了Stacking血红蛋白浓度检测模型,以实现血红蛋白浓度的准确测量。基于多波长PPG信号的血红蛋白无创检测原理见图1。

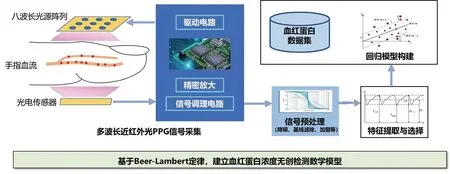
图1 基于多波长PPG信号的血红蛋白无创检测原理图

1 血红蛋白浓度无创检测原理

基于PPG的检测方法的理论基础是Beer-Lambert定律,其大致步骤为:通过Beer-Lambert定律推导出血红蛋白检测模型,并以此模型为指导进行特征信息的提取与回归预测模型的构建。提取的特征信息主要包括时域、频域、形态和幅值信息[5-6]等。同时,为降低特征冗余,常采用主成分分析等方法提取关键核心特征[6],以提高模型的预测能力。通常基于机器学习算法构建预测回归模型[13],常用方法包括偏最小二乘法[14]、BP神经网络[15]、支持向量机(support vector machine,SVM)[16]以及集成学习。

1.1 Beer-Lambert定律

Beer-Lambert定律描述的是物质的吸光程度与物质的浓度、光在物质中的传播路径长度之间的关系,可表示为:

I=I0e-ε(λ)cd

(1)

式中,I0为入射光的强度,I为出射光的强度,ε(λ)为物质对波长为λ的光的摩尔消光系数,c为吸光物质浓度,d为光在介质中传播的路径长度,称为光程长。

对式(1)进行变换得到吸光度A为:

(2)

当被测样品中含有多种物质时,样品对光的总吸收度At为每种物质单独对光的吸收度之和,即:

At=ε1(λ)c1d+ε2(λ)c2d+…+εn(λ)cnd

(3)

式中,εi(λ)为第i种物质对光的消光系数,ci为第i种物质的浓度。对第i种物质,其对波长为λ的入射光的消光系数εi(λ)为常数。

1.2 基于Beer-Lambert定律的血红蛋白浓度检测原理

光在人体组织中传播,人体表皮、真皮、肌肉、脂肪、骨骼、血液等组织会对其产生吸收与散射作用,血红蛋白是血液中的主要成分,其对光的吸收作用会随动脉血的搏动而变化,而皮肤、肌肉、脂肪、骨骼等组织对光的作用是恒定的,因此,可通过测量吸光度的改变量去除皮肤等非跳变组织的影响,实现血红蛋白浓度信息检测。假设入射光波长为λ1,因动脉血搏动引起的吸光度变化量可表示为:

ΔA1=[ε1,1(λ1)c1+ε1,2(λ1)c2]Δ

(4)

式中,c1,c2分别为含氧血红蛋白浓度和还原血红蛋白浓度,Δ为因动脉血搏动引起的平均光程长的变化量,ε1,1(λ1)为含氧血红蛋白对λ1波长光的吸光度,ε1,2(λ1)为还原血红蛋白对λ1波长光的吸光度。

对大部分健康人而言,总血红蛋白浓度可看作含氧血红蛋白浓度和还原血红蛋白浓度之和。当采用多个波长光源时,可得到不同波长光源下的吸光度变化量,进一步推导,可得总血红蛋白浓度为:

ctHb=f(R12,…R1N,R21,…R2N,…RN1,…RN,N-1)

(5)

(6)

其中,ACλi和DCλi分别为光波长为λi获取到的PPG信号的跳变成分(AC)和非跳变成分(DC)的幅值强度。

由上述推导结果可知,血红蛋白浓度与特征值Rij呈映射关系,而特征值Rij可由检测到的PPG信号计算得到。

2 多波长PPG信号采集系统设计

为采集不同波长下的PPG信号,本研究设计了八波长PPG信号采集系统,系统主要包括多波长PPG传感器、多波长信号调理电路、LED驱动电路以及信号预处理模块,原理框图见图2。选取波长在600～1 000 nm间的近红外LED作为光源,波长分别为610、630、660、690、750、805、850和940 nm,采用时间复用机制对人体组织进行轮询发光照射,通过光电探测器对组织出射光进行探测。

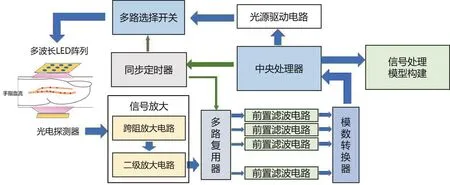
图2 多波长PPG信号采集系统框图

3 模型构建

3.1 PPG信号预处理

PPG信号主频率通常为1～10 Hz。为滤除PPG信号中的噪声干扰,本研究首先采用截止频率为10 Hz的有限冲激响应低通滤波器滤除高频噪声。然后,采用小波变换对基线漂移进行消除,首先利用“coif5”小波对输入PPG信号进行分解,在尺度为7及以上时,信号主要为基线漂移成分,因此,将PPG信号分为7层后,将第7层逼近系数置零,然后将剩余层进行小波重构,得到去除基线漂移的PPG信号。

3.2 特征信息提取与选择

3.2.1特征信息提取 本研究采用八个波长的近红外光获取血红蛋白浓度信息,根据推导的血红蛋白浓度检测模型,从八个波长光源产生的PPG信号中提取特征信息Rij,首先对预处理后的八个PPG信号进行加窗处理(窗长为5 s),截取有效数据,然后计算特征值信息Rij,采用差分方法提取AC成分,以PPG信号的幅值平均值作为DC成分,八个波长的通道数据可获得56个特征信息。由于血红蛋白浓度与人的年龄和性别有关,本研究同时将患者的年龄和性别也作为血红蛋白浓度检测的特征信息。

3.2.2特征信息选择 为减少冗余信息,本研究采用基于序列后向选择思想的递归特征消除SVR-RFE(support vector regression-recursive feature elimination,SVR-RFE)算法对提取的特征信息进行选择,该方法基于特征信息的重要性选择特征,每次循环删除一个重要性最小的特征,形成新的特征集,并通过遍历所有的特征集,选出能够获得最佳预测结果的特征集,具体流程图见图3。

图3 SVR-RFE算法流程图

通过SVR-RFE特征选择算法,本研究从58个特征中选出对血红蛋白浓度预测贡献最大的特征集,当特征数量为29,则选取前29个贡献率最高的特征时,SVR模型的预测精度达到最高,因此,本研究选择前29个贡献率最大的特征进行回归建模。

3.3 构建基于Stacking集成学习的回归模型

为提高回归模型的预测性能,本研究采用Stacking集成学习算法,构建血红蛋白浓度无创检测模型。采用多层模型架构,通过元回归器整合多个回归模型,以提高模型预测性能。第一层采用多元线性回归、Ridge回归、AdaBoost回归三种不同模型,保证模型的泛化能力;第二层采用支持向量回归SVR模型作为元回归器。第一层回归模型的预测结果作为第二层元回归器的输入值,以获得更准确的预测值。模型见图4。

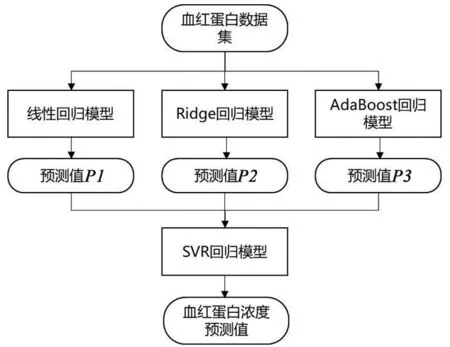
图4 基于Stacking学习的血红蛋白浓度预测模型

3.3.1多元线性回归模型 多元线性回归是一种常用的线性回归方法,其研究的是多个自变量和因变量之间的线性关系,以使多个自变量Xi的加权和与因变量Y之间的均方根误差最小,用数学表示为:

Y=β0+β1X1+…+βmXm+ε

(7)

通常采用最小二乘法来寻找最佳回归系数β0,β1,…,βm使得残差ε最小。

当今世界，不同的国家面临着不同的国情。即使在同一国家乃至同一地区，也会呈现出民族、文化、每个人所处的具体社会地位的多样性，由此也引发了利益分歧的多样性，尤其是价值观念的多样性。而价值观，是以一定文化的内核乃至核心的形式呈现出来的。在此意义上，这种多样性的价值观念，为各个国家和地区开展协商民主、达致多元共识提供了重要的文化条件。这也正如当代美国协商民主研究领域的知名学者詹姆斯·博曼所言:“多样性甚至能够促进理性的公共运用，并使民主生活更加充满活力。”这一观点，不仅揭示了价值观念的多样性同民主特别是协商民主之间的内在联系，也表征了西方学界对于二者关系具有代表性的认知。

3.3.2Ridge回归模型 Ridge回归模型是一种改进的线性回归模型,为解决线性回归中的过拟合及自变量共线性而导致的无法求解问题,其在求解过程中加入了正则化,可表示为:

(8)

3.3.3AdaBoost回归模型 AdaBoost回归是一种集成的学习方法,通过集成多个弱学习器提高学习器总体性能。AdaBoost算法在优化迭代过程中,通过对样本的权重进行不断调整,增大使弱学习器误差大的样本权重,以使误差大的样本在下次训练中得到重视,以更好地拟合数据模型。AdaBoost回归可以拟合非线性关系。其原理如下:

(1)输入:训练集D={(x1,y1),(x2,y2),…,(xm,ym)}, 弱学习器G,迭代次数T;

(3)Fort= 1,2,…,T:

根据样本分布Dt训练弱学习器Gt;

(9)

更新样本权重:

(10)

(4)输出:强学习器

(11)

其中,g(x)为所有αtGt(xi)的中位数。

3.3.4SVR回归模型 SVR是一种基于SVM的回归算法。它通过寻找将数据划分为两类的超平面,发现回归问题中的最佳拟合曲线,从而将预测误差降至最低。SVR的核心思想是在核函数的作用下,将低维特征空间中线性不可分的样本映射到高维特征空间,使其线性可分。SVR可表示为:

(12)

式中,C为正则化常数,lε为ε的不敏感损失函数:

(13)

4 实验验证与结果

4.1 数据采集

本研究选取参加医院体检的249例志愿者作为实验对象。实验开始前,受试者需要静息5 min,在测量过程中,对受测者的一只手进行指端末梢采血20 uL,同时对另一只手使用本研究的多波长PPG信号采集系统进行2 min的信号采集并保存,采集的血液样本通过全自动血细胞分析仪(XS-1000i,希森美康)对血红蛋白浓度进行检测,由此获得血红蛋白浓度的检测值作为真实参考值。受试者的身体基本情况见表1。

表1 受试者的身体统计情况

4.2 实验结果

将采集到的249例样本数据按照8∶2比例随机划分为训练集和测试集,其中训练集包含199例样本,测试集包含50例样本。

采用训练集对回归预测模型进行训练,采用测试集对模型的性能进行评价,最后得到测试集均方根误差为1.17 g/dL,相关系数为0.75(P<0.01)。图5为对测试集样本进行预测的结果图,横坐标为传统方法检测的血红蛋白参考浓度,纵坐标为模型预测的血红蛋白浓度值。

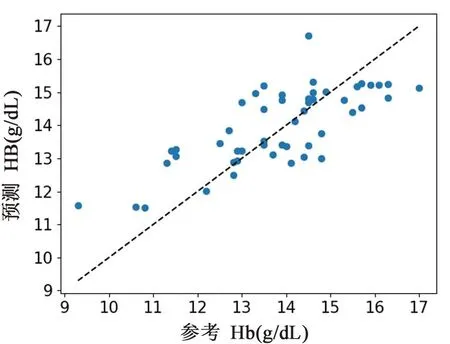
图5 血红蛋白浓度参考值与预测值散点图

图6为血红蛋白浓度参考值与模型预测值之间的Bland-Altman描述图,横坐标为预测值和真实值的平均值,纵坐标为预测值与真实值之间的差值。可见,大部分测试数据都在95% 一致性界限内,表明两种方法具有较好的一致性。

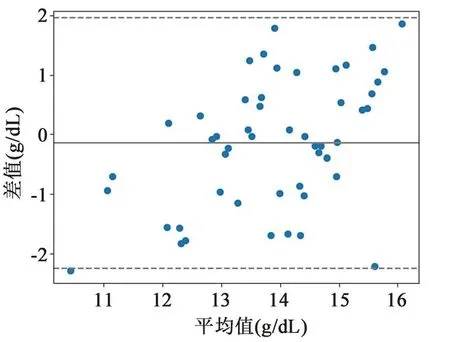
图6 参考值与预测值的Bland-Altman描述图

为进一步验证本研究方法在无创血红蛋白检测中的有效性,将其与线性回归(linear regression, LR)、随机森林(random forest, RF)和SVR方法进行了对比,结果见图7。实验结果表明,采用本研究方法可获得更准确的预测结果。

5 结论

本研究提出了一种基于多波长近红外光谱的无创血红蛋白浓度检测方法。首先,基于Beer-Lambert定律推导了血红蛋白浓度无创检测模型,并基于该模型设计了八波长近红外光PPG信号采集系统;然后,滤除PPG信号中的高频噪声和基线漂移,并根据建立的无创检测模型对特征信息进行提取与选择;最后,采用Stacking算法建立了血红蛋白浓度检测模型。通过采用199例样本数据对模型进行训练,采用 50例样本数据对模型进行测试验证,得出预测血红蛋白浓度值与传统检测方法的均方根误差为1.17 g/dL,相关系数为0.75(P<0.01)。实验结果表明,本研究设计的血红蛋白无创检测模型与传统检测方法具有较强的一致性,可为贫血筛查、术中输血动态监测等临床应用提供一种新的选择。