悬臂结构地震响应分析的广义单自由度模型研究

吴承宇,何 军

(上海交通大学 船舶海洋与建筑工程学院土木工程系,上海 200240)

悬臂结构是工程中常见的一种建筑结构,如水塔、烟囱、输电塔,甚至高层建筑,在进行其地震响应分析的时候,可以将它们处理为悬臂结构。悬臂结构的地震响应分析一般通过有限元方法来进行,但是,有限元分析往往需要较长的计算时间,这对于需要运行多次受力性能分析的情况(如结构可靠度计算或结构易损性评估等),会带来计算费用过大的问题。因此,建立悬臂结构地震响应分析的简化模型,对提高悬臂结构地震响应和抗震性能分析的效率,具有重要的意义。

悬臂结构地震响应分析的简化方法包括振型分解反应谱法、底部剪力法、推覆分析方法和广义单自由度模型方法等。李明政等[1]利用振型分解反应谱法和时程分析法计算料仓-框架结构的地震响应,并针对其位移和应力进行比较,给出时程分析比振型分解反应谱法分析更加精确的结论。马安财等[2]提出了相应地震响应分析的振型叠加法,结合一实际深水隔震连续梁桥,通过与有限元计算结果对比,验证了该方法的有效性。1920年,日本学者大森房吉提出基于结构底部剪力法的静力理论,美国加州1952年的侧力规范采纳了底部剪力法。夏仕洋等[3]基于底部剪力法提出了对阻尼器参数进行优化的简化方法,并通过时程分析法对结构的抗震性能进行了验证。早在1975年,Freeman[4]提出了推覆分析法,用于评估地震活动频繁区域的建筑物的抗震性能。黄超等[5]用推覆分析方法对结构进行静力弹塑性分析,根据力-变形关系和侧向位移形状函数,确定了等效单自由度模型的相关系数。张大巍等[6]采用弹塑性静力推覆分析法和弹塑性时程分析法对某典型发电厂主厂房的抗震性能进行评估。广义单自由度模型方法较早由Clough等[7]提出,他们将实际体系的响应分析归入广义单自由度类型,即当体系运动限制为单一变形形式时,在数学意义上只有一个自由度。程鹏飞等[8]以某大型斜拉桥为工程实例,基于一阶振型的广义质量和广义刚度发展了广义单自由度模型,分析了梁端位移和塔梁相对位移。与全桥模型进行对比分析后,验证了广义单自由度模型的可行性。王赞芝等[9]利用振型函数,将具有分布质量的弹性体转化为一个广义单自由度振动系统,并提出了一种计算简支梁在均布随机荷载下位移极值响应的方法。Song[10]和Der Kiureghian等[11]采用广义单自由度模型建立了变电站一次设备支架结构地震响应分析的快速方法。

本研究聚焦于悬臂结构地震响应的快速分析,强调广义单自由度模型的形函数选择对准确性的关键影响。针对当前缺乏通用形函数模型的问题,本文提出了基于多项式形函数的广义单自由度模型,并深入研究了其在不同地震波激励下的有效性。通过此项研究,旨在为结构抗震性能的评估提供更准确、快速的分析工具。

1 广义单自由度模型简介

如图1所示,本文研究的广义单自由度模型将悬臂结构简化成一个由质点、弹簧、阻尼组成的单自由度系统,质点只有一个水平自由度,质点与地面之间由一个无质量的弹簧和阻尼单元连接。

图1 悬臂结构的广义单自由度模型

在广义单自由度模型中,结构位移响应被表示为X(y,t)=φ(y)z(t),其中的y为距地面的距离(高度),φ(y)为位移形函数,z(t)是反映位移形状随时间变化的广义坐标。由虚功原理,可以得到广义单自由度模型的等效质量m、等效刚度k、等效阻尼c和产生外部惯性力的等效质量l的计算式[10]

(1)

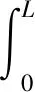
(2)

(3)

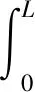
(4)

式中,L为结构高度,m;ρ(y)为线密度,kg/m;EI(y)为抗弯刚度函数,N·m2;φ(y)为位移形函数。

由此,可将悬臂结构的运动方程简化为

(5)

对于悬臂结构,形函数φ(y)应该满足几何边界条件φ(0)=0,φ′(0)=0和φ(L)=1,另外,形函数φ(y)还应该满足力的边界条件φ″(L)=0和φ‴(L)=0。由于实际工程中悬臂结构的高宽比较大,在水平地震作用下,其横向弯曲变形为主导,而剪切变形对结构的影响可以忽略不计,因此可以不考虑力的边界条件φ‴(L)=0。

对于悬臂结构,常用的位移形函数类型是抛物线形函数和三角函数形函数[12]:

(6)

和

(7)

式中,y0为结构某部位的高度,m;L为结构总高度,m。

抛物线形函数通常被假设为近似描述结构位移分布的二次曲线形式。它假设结构的位移在横向上均匀分布,并具有对称的曲线形状。然而,在实际情况下,结构的变形可能呈现非线性和非对称的特征,抛物线形函数无法准确描述这些复杂的变形模式,从而导致精度不高。

三角函数形函数是另一种常用的位移函数类型。它以正弦函数和余弦函数为基础,通过调整振幅、频率和相位来适应结构的变形特征。三角函数形函数常用于描述周期性或周期性近似的位移分布,如梁的弯曲振动或柔性结构的模态形态。然而,这种假定限制了位移分布的形式,虽然它满足端点的几何边界条件,但却不是一个符合实际的假设。

2 多项式形函数

考虑到上述两种位移形函数的局限性,并结合悬臂结构的几何边界条件和力的边界条件,本项研究提出一种多项式形函数:

(8)

式中,a和b为待定系数,y0为结构特定部位的位置(高度),m。

高度y0由所考虑的地震响应的位置确定。如果考虑结构顶部的地震响应,则y0等于结构的高度,而当考虑结构中间位置地震响应的时候,y0应等于结构高度的1/2。系数a和b由结构静力反应计算结果或基本振型计算结果确定。因为结构静力反应或基本振型的计算费用比较少,因此,可以由较少的计算费用确定待定系数a和b。注意,为满足边界条件φ(y0)=1,系数a和b应满足关系式a+b=1。

公式(8)定义了只包含二次和三次项的三次多项式函数。满足几何边界条件φ(0)=0,φ′(0)=0和φ(y0)=1 以及力的边界条件φ″(y0)=0。公式(6)和公式(7)所定义的抛物线形函数和三角函数形函数,分别是基于悬臂结构在自由振动时的挠曲形状的假设以及在悬臂结构的顶点受到单位侧向力作用引起的挠度公式所计算得出的。其中,后者的计算精度相对较高。然而,本研究提出的多项式形函数则是通过从有限元计算结果中提取结构位移并进行拟合而得到。相较于前两种形函数,多项式形函数改善了公式形式单一固定、通用性低等缺点。

3 基于多项式形函数的广义单自由度模型

下面以理想化变截面悬臂结构为例,说明基于多项式形函数的广义单自由度模型的建模过程。

3.1 结构的设计参数

考虑图2(a)所示的底部固接上端自由的变截面悬臂钢杆。杆的总高L=10 m,顶端圆截面半径R1=0.2 m,底端圆截面半径R2=0.3 m。钢材弹性模量E=2×1011Pa。钢杆沿y轴的线密度ρ(y)=123.3y+914.5 kg/m,截面惯性矩I(y)=2.962×10-5y2+1.916×10-4y+0.001 25 m4。悬臂钢杆采用梁单元建模(采用ABAQUS软件),具体有限元模型示意图如图2(c)所示,该模型被平均离散成20个单元和21个节点。

图2 悬臂钢杆

3.2 多项式形函数的系数计算

在有限元分析中,为了确定悬臂结构在水平集中荷载作用下的位移响应,将集中荷载施加在结构顶端,提取每个节点的位移值,并计算位移形函数。然而,实际工程中需要的是结构特定部位的位移响应,该响应是由结构上附属设备位置y0所决定。因此,选取了高度10 m作为实际工程中的典型位置,即悬臂结构的顶端位置,令该处的形函数φ(y0)的值等于1,并对形函数进行归一化。归一化的结果如图3所示。将图3中的归一化形函数结果拟合成本研究提出的公式(8)的多项式形式,并通过边界条件确定待定系数a和b。通过此方法,得到了在水平集中荷载作用下多项式形函数的待定系数,分别为a=1.501 7和b=-0.501 7。按同样的方法由有限元分析结果确定基本振型和倒三角分布荷载作用下的位移形函数。

图3 多项式形函数曲线

3.3 广义单自由度模型的参数计算

根据3.2节确定多项式形函数的待定系数a和b后,由公式(1)—(4)对多项式形函数进行积分求解,求得多项式形函数分别在集中水平荷载、基本振型、倒三角分布荷载作用下的等效参数m、c、k和l,计算结果列于表1中。

表1 单自由度模型的等效参数

4 基于多项式形函数的广义单自由度模型的有效性分析

本节通过对比由有限元模型和广义单自由度模型得到的最大响应,调查基于多项式形函数的广义单自由度模型的有效性。

4.1 输入地震波

地震动记录的选取准则主要考虑场地土类别、震级、地震动峰值加速度、地震波持时等因素。如表2所示,本项研究选择了I—IV类场地土类别和6—8级震级范围内的12条自然地震波作为悬臂结构有限元模型和广义单自由度模型的输入地震波。

表2 选取的地震动记录

4.2 结构地震响应

假设结构特定高度处的水平地震响应为u(t),极值为

(9)

式中,T为地震波持时,s。

有限元模型的地震响应由模态叠加法进行求解,为保证每个方向上各阶模态参与质量系数大于90%,本项研究选取前5阶模态进行分析。广义单自由度模型的地震响应采用杜哈梅积分进行求解。根据表1中水平集中荷载的计算结果,分别计算12组地震波作用下悬臂结构广义单自由度模型和有限元模型的地震响应。表3给出了由基于抛物线形函数(公式(6))、三角函数形函数(公式(7))和多项式形函数(公式(8))的广义单自由度模型和有限元模型计算的高度10 m处的最大位移响应。San Fernando地震波输入下的位移响应绘于图4中。

表3 基于不同形函数模型的最大位移响应和相对误差

图4 地震响应对比

4.3 广义单自由度模型的有效性分析

表3的计算结果表明,基于多项式形函数的广义单自由度模型的最大位移响应,其计算结果的最小相对误差为1.21%,最大相对误差为22.10%,平均误差为7.20%,而基于抛物线形函数和三角函数形函数的广义单自由度模型的平均相对误差分别为27.06%和15.93%。由图4可以看出,基于多项式形函数的广义单自由度模型和有限元模型的时程曲线吻合程度较好,结构10 m位置的位移响应极值非常接近。

图5绘出了表3中每条地震波激励下基于多项式形函数的广义单自由度模型和有限元模型的位移响应最大值Umax、变异系数C·V和均方根误差RMSE。图5表明,基于多项式形函数的广义单自由度模型计算结果与有限元模型计算结果的均方根误差RMSE很小,这意味着两种模型之间具有很高的相似性,进一步说明了基于多项式形函数的广义单自由度模型在地震响应分析中具有优势。同时,该模型的变异系数C·V为0.81,表明数据点之间存在较大的离散性。

图5 有限元分析和广义单自由度模型的最大位移响应

为了进一步调查多项式形函数的适用性,分别利用水平集中荷载作用、基本振型和倒三角分布荷载作用下的有限元模型分析结果,拟合生成形函数,构造三个广义单自由度模型。表4列出了三个广义单自由度模型的计算误差,结果显示,基于水平集中荷载作用下多项式形函数的广义单自由度模型的整体平均误差明显小于其他两种模型。三个广义单自由度模型计算结果的均方根误差RMSE分别为0.39、3.13、2.81 mm,基于水平集中荷载作用下形函数的广义单自由度模型的均方根误差最小。

表4 基于不同形函数提取方法的最大位移响应和相对误差

5 结论

1)在建立广义单自由度模型方面,与常用的抛物线形函数和三角函数形函数相比,本文提出的多项式形函数具有更高的精度,能够快速地拟合出满足边界条件的多项式函数曲线,并且对不同类型地震波输入的适用性更加广泛。

2)在进行多项式形函数参数估计时,建议通过对结构施加水平集中荷载,计算结构的水平变形形状。