不确定性中的确定性∗
——中国经济风险识别
隋建利 吕文强 刘金全
一、引言
近年来,伴随着中美贸易摩擦、新冠肺炎疫情等一系列极端风险事件的发生,中国经济稳增长压力日益增加。国家统计局发布的数据显示,2023 年第三季度中国GDP 同比增长4.9%,增速较2023 年第二季度回落1.4%,意味着现阶段中国经济的增长压力及增长风险仍在进一步上升。面对世界经济复苏缓慢、全球疫情持续演变、外部环境纷繁复杂的现实,如何抵御风险的渗透冲击,保持经济平稳健康的发展态势,关乎当下的国计民生。2023 年《政府工作报告》明确指出,目前中国经济正面临需求收缩、供给冲击、预期转弱“三重压力” 的严峻形势,必须正视外部与内部不确定性的交织,在不确定性中谋求确定性,从而有效应对各种风险挑战,保持经济在合理区间运行。2023 年12 月,习近平总书记在中央经济工作会议上再次强调,要以经济安全为基础,坚持“稳” 字当头、稳中求进的工作总基调,着力防范和化解重大经济风险,进而实现“稳增长” 与“防风险” 的双重目标。可以看出,有关不确定性与经济风险之间关系的讨论,已然成为国家和政府各部门关注的重要议题。在此背景下,探究不确定性对经济风险的潜在影响,对于深入贯彻党的二十大精神,强化风险监管与预期管理,促进经济高质量发展与高水平安全良性互动,实现中国式现代化具有重要的指导意义。
不确定性能够对经济主体的投资与消费决策产生重要影响,继而与经济增长存在显著关联(Bloom 等,2018),因此不少研究聚焦于探索不确定性影响经济增长的理论机制。其中,不确定性对经济增长的传导途径存在四种不同的理论逻辑,分别为具有促进作用的Hartman-Abel 效应理论和增长期权理论,以及具有抑制作用的实物期权理论和风险规避理论。具体而言,Hartman-Abel 效应理论是指,在企业能够根据经济形势灵活调整生产规模的情况下,伴随着不确定性的升高,企业会更加关注随之而来的投资机会与潜在利润,这使得企业的期望边际收益得以增加,从而对经济增长产生积极影响(Hartman,2006)。增长期权理论是指,未来前景不确定性使得企业为了实现长期生产经营,不断加大研发投入,以期保证产品或服务的持续创新,这可视为增长期权的积累过程,可以为企业带来较高的预期利润,进而促进经济增长(Smit 等,2017;顾夏铭等,2018)。实物期权理论是指,经济主体的投资与消费机会可被视作一系列实物期权,不确定性的增加会使经济主体看跌期权价值,从而延迟投资与消费,最终引致经济增速下降(刘贯春等,2022)。风险规避理论是指,对于投资者而言,不确定性使得投资者要求更高的风险补偿,导致企业融资约束及成本提高,进而引发金融市场收紧(Lhuissier 和Tripier,2021;Di Maggio 等,2022;谭小芬等,2022);对于消费者而言,不确定性能够诱发消费者的预防性储蓄和风险厌恶偏好,降低消费者投资、消费意愿,继而抑制经济增长(Mumtaz 和Theodoridis,2018;Angelini 等,2019)。然而,尽管上述理论研究成果丰硕,但是都无一例外地将不确定性视为独立于经济主体的外生变量,鲜有研究从企业行为等微观视角出发,探究经济系统中不确定性的生成机制,以及其影响经济增长的微观机理。
在探究不确定性影响经济增长的相关研究中,不确定性指标的选取至关重要。部分学者通过计算单一宏观变量的波动性来衡量不确定性,例如采用股票市场指数、通货膨胀以及GDP 等变量的波动率作为经济不确定性的代理指标(Chen 等,2020;王晓宇和杨云红,2021)。尽管计算简单方便,但是基于波动性的测度方法没有剔除宏观变量的可预期成分,这与不确定性的本质,即经济系统中无法预期的部分并不相符。为了克服上述局限,国内外学者从不确定性的定义出发,利用GARCH 以及VAR 族等计量模型对宏观变量的预测误差进行估计,并将预测误差作为不确定性的代理指标。具体地,已有研究使用股票收益率、利率以及工业增加值等变量的条件波动率来反映不确定性水平(王义中和宋敏,2014;Scotti,2016)。尽管预测误差能够充分体现不确定性中的“非预期性”,但是具体的预测误差可能过度依赖于特定的经济指标,因此这种度量方式难以表征经济系统整体的不确定性水平。有鉴于此,Jurado 等(2015)基于高维因子模型对大规模经济变量的非预期条件波动率进行估计,并测度经济系统中不可预测成分的共同波动,即经济不确定性。此后,相关研究运用高维因子模型分别衡量了中国的经济不确定性水平(Huang 等,2018;赵文佳和梁燚焱,2020)与金融不确定性水平(黄卓等,2018)。然而,通过梳理能够发现,已有研究多聚焦于经济不确定性的度量,而对金融不确定性的测度分析明显偏少。事实上,无论是就产生机理、波动特征还是经济效应而言,经济不确定性与金融不确定性都存在着显著差异(Alessandri 和Mumtaz,2019;Ludvigson 等,2021),但是,国内文献目前对此明显探究不足。
随着不确定性对宏观经济的影响日趋复杂,基于不同视角探究不确定性影响经济增长的实证研究不断涌现。国内外学者运用传统计量模型以及动态随机一般均衡(DSGE)模型等方法,分析了不确定性对经济增长的冲击效应。结果发现,不确定性对实体经济表现出明显的逆周期性,能够对经济增速产生显著的负向影响(Hristov 和Roth,2022;王博和徐飘洋,2022)。然而,相关研究均是从点估计的视角出发,在本质上揭示的是不确定性对经济增长“期望值” 的影响,而忽略了从区间估计的视角探究不确定性对经济增长“风险值” 的潜在影响。事实上,伴随着外部环境的深刻变化,全球经济形势愈加复杂。在此背景下,刻画不同风险水平下经济增长的运行状况,揭示经济增长的潜在风险变得极为重要。有鉴于此,国际货币基金组织(IMF)根据在险价值(value at risk,VaR)的概念提出了在险增长(growth at risk,GaR),即将经济增长视为一种概率分布形式,并利用相应的条件变量来预测未来经济增长的概率分布曲线,旨在衡量宏观金融形势对经济风险的潜在影响(IMF,2017)。Adrian 等(2019)从经济增长概率分布出发,运用条件分位数回归模型,分析了经济和金融状况对经济风险的相关影响。随后,国外学者基于概率分布的视角,探究了不同宏观变量对经济风险的影响作用(Adams 等,2021;Jovanovic 和Ma,2022)。反观国内的研究领域,目前仅有张晓晶和刘磊(2020)从概率分布的视角,探讨了金融风险对经济增长特定“风险值” 的影响,而现有文献缺乏对经济风险的系统性分析,亦缺少探究不确定性对经济风险的影响研究。
通过梳理已有文献能够发现,现有研究仍存在一定的局限性。首先,以往研究大多将不确定性视为独立于经济系统的外生冲击,未能从经济主体层面探究不确定性的生成机制,因而无法将不确定性与经济增长置于统一的内生框架分析其内在机理。其次,已有研究多采用经济不确定性及其代理指标检验不确定性的经济效应,鲜有文献在大数据估计的基础上,基于中国经济不确定性与金融不确定性的分离测度视角,探究其对经济风险的异质性影响。最后,既有研究多基于传统计量模型展开,从点估计的视角出发,分析不确定性对经济增长“期望值” 的冲击效应,鲜有研究基于区间估计的视角,将经济增长视作一种概率分布形式,探究不确定性对经济风险的潜在影响。
鉴于上述分析,本文具有如下可能的创新:第一,提出内生不确定性的概念,并将经济增长视为一种概率分布形式,基于不确定性与经济增长的统一分析框架,阐明不确定性影响预期经济增速分布的理论机制。第二,基于高维因子模型,构建中国经济不确定性与金融不确定性指数,进而辨析经济不确定性与金融不确定性对经济风险的异质性影响。第三,运用条件分位数回归模型,分别将经济不确定性与金融不确定性作为预期经济增速分布的条件变量,继而通过在险增长、相对熵值以及期望损失等模型,揭示不确定性冲击下经济风险的确定性特征。第四,基于理论模型与经验事实的综合分析,探究不确定性对经济风险的时变冲击效应,刻画不确定性对经济风险的驱动机制。因此,本文研究具有如下的贡献与价值:在理论意义层面,引入内生不确定性概念以及经济增长的概率分布形式,丰富不确定性影响经济增长的微观理论基础,拓宽相关领域的研究视角和研究思路;在现实意义层面,分离构建并探究经济不确定性与金融不确定性对经济风险的潜在影响,不仅有助于中国应对“三重压力”,防范和化解重大经济金融风险,保障经济运行在合理区间,而且能够为中国各部门推出有利于经济稳定的政策提供重要的理论依据与经验支持。
二、理论模型
为了从理论上刻画不确定性的产生及其对经济增长的影响,本文参考Jovanovic 和Ma(2022),将不确定性与经济增长置于统一框架下,构建涵括内生不确定性的经济增长模型。其中,理论模型具有一个重要特征,即不确定性与经济增长均为内生变量,不确定性来源于经济系统中技术水平的更新过程。
(一)代表性厂商
考虑一个具有消费偏好的代表性厂商,其目标是最大化终生效用,目标函数可表示为:
在此,E0代表期望算子;β为跨期贴现率,以反映未来效用与当期效用之间的替代弹性;ct表示厂商在第t期的实际消费。假定厂商只生产一种商品,产出水平取决于技术水平A和技能组合h。其中,技能组合在本质上强调的是技术水平与投入要素(包括劳动和资本投入)之间的匹配程度,匹配程度越高,技能组合越优,产出水平越高。因此,潜在产出yp能够表示为:
其中,sA表示与技术水平A相匹配的最优技能组合,具体表示能够在技术水平A下实现最大产出的技能组合。λ代表惩罚系数,h′为当期技术水平的实际技能组合,λ(sAh′)2/2 刻画了厂商实际技能组合与最优技能组合间存在的“技能缺口” 导致的损耗产出。厂商能够选择以x(x≥0)的速度提高其技术水平,从当期的技术水平A开始,下一期的技术水平A′可以表示为:
在此,考虑到更新后的技术水平与厂商现有投入要素的禀赋匹配程度是不可预测的,即更新后的新技术与先前投入要素的匹配程度既可能升高又可能降低,并且只有在厂商采用新技术之后,技术对投入要素的需求才会清晰展现。因此,本文假定更新的技术水平A′对最优技能组合的影响是随机的,即sA′服从随机游走分布:
其中,ε~F(ε),服从均值为0、方差为σ2的独立同分布。厂商在观察到ε前选择是否更新技术,一旦更新到技术水平A′,厂商就无法再采用上一期的技术水平A。因此,假定厂商以技能组合h开始进行生产,进一步地,厂商可以选择调整技能组合至h′。在此过程中,h′=h+Δ,假定厂商更新技术水平以及技能组合存在投入成本C(yp,Δ),并且投入成本与潜在产出水平以及更新技能组合的变化幅度密切相关,其能够表示为:
因此,厂商的净产出可以表示为:
其中,u=SA-h是最优技能组合与实际技能组合之间的差值(以下简称“技能缺口”)。
(二)内生不确定性
厂商的状态可以利用技能缺口u与技术水平A表示,厂商的决策为(x,Δ)。此外,厂商没有任何形式的资产,其消费与产出水平相等。因此,厂商的最优动态方程为:
进一步地,可以得到:
并且,φ=(λα2+θ(1-α)2)/2。
厂商以不变速度x更新技术水平,其中,更新技术水平与技能组合的直接成本Δ与当期的技能缺口u成正比。根据式(4),技能缺口u服从AR(1)过程:
由于厂商的状态可以利用技能缺口u与技术水平A表示,厂商的决策为(x,Δ)。对于技能缺口u=sA-h而言,最优技能组合sA的变化取决于厂商决策x,而实际技能组合h则取决于厂商选择的投入成本决策Δ。能够发现,技能缺口u是经济系统中的内生变量。因此,本文利用内生技能缺口u的方差对不确定性进行刻画。由于α介于0 至1 之间,技能缺口ut是平稳的,其方差为:
其中,式(13)中的第三个等式由式(8)推导得到。直观而言,σ减小能够导致x增加,使得厂商技术水平的更新速度加快。同时,技术更新加速会导致技能组合SA′更加难以预测,从而致使技能缺口的方差增加。需要注意的是,正是由于厂商的行为,尤其是厂商更新技术的投资决策(x,Δ),使得技能缺口存在波动,进而导致经济运行产生相应的不确定性。不难发现,不确定性来源于经济系统内部厂商的技术更迭。进一步地,考虑将经济中的代表性厂商扩展为无限个,全部厂商起始时都处于相同状态(u,A),假定所有厂商都进行相同决策,均衡将完全对称,此时经济中只存在总体风险。而在每个时点上,对于全部厂商而言,x的选择和ε的观测值将完全一致,调整技能组合h将无法使其获利。
(三)预期经济增速分布
假定C(yp,Δ)完全由技术水平与技能组合调整引致的产出损耗构成,能够得到总产出的对数值:
其中,φ=(λα2+θ(1-α)2)/2。式(14)表明,产出水平取决于常数项A0、时间趋势项t以及技能缺口。因此,本文可以利用包含常数项和时间趋势项的回归模型估计lnyt。式(14)中,技能缺口的平方项可以解释为预测误差。由于ut是平稳的,因此lnyt同样趋势平稳,其趋势为产出水平的长期增长率x。进一步地,经济增长可以表示为:
式(15)表明,经济增长不仅取决于技术水平的更新速度x,而且还会受到技能缺口平方项变动的影响。不难发现,技能缺口的减小能够促进经济增长,然而,调整技能组合需要付出成本,特别是当下一期的技能组合出现意外降低时,产出水平将明显下降。因此可以推断,当参数θ较大时,经济增速分布具有负向偏斜倾向。具体地,在初始产出水平y0与技术水平A0的条件下,εt服从正态分布N(0,σ2),预期经济增速分布gt可以表示为:
其中,ξt~N(0,1),并且考虑到φ>0,ξt服从正态分布,服从自由度为1的卡方分布,因此,预期经济增速分布gt负向偏斜,并且服从非中心化的卡方分布。本文使用非中心化卡方分布中不同分位数的估计值,能够得到预期经济增速分布的相关表达式,具体包括5%分位数的预期经济增速χt、预期经济增速均值E(gt+1)、预期经济增速波动率V(gt+1)以及预期经济增速分布的4 分位距IQR(gt+1)。需要说明的是,遵循Adrian 等(2019),本文将t期的在险经济增长率χt定义为t+1 期预期经济增速分布的下5%分位数(即5%分位数的预期经济增速),以表征经济下行风险。因此,在均衡状态下,预期经济增速的相关分布满足:
因此,根据式(17)至式(20)可知,5%分位数和均值预期经济增速伴随着不确定性的升高而下降,预期经济增速分布的波动率和4 分位距则伴随着不确定性的升高而增加,即:
当时间趋于无穷时,即在长期的预期经济增速分布gt中,经济增速不取决于初值u0,而是满足:
其中,当且仅当α<1 时,上述预期经济增速的相关分布有界,能够表示为:
lim
三、中国经济不确定性与金融不确定性的指数构建
(一)不确定性指数的构建方法
为构建中国经济不确定性与金融不确定性指数,本文参考Jurado 等(2015)的研究,通过建立高维因子模型,实现对经济不确定性与金融不确定性水平的分离测度。具体而言,对于一个经济或金融变量序列yit,其未来n期的不确定性Uy jt(n)可以表示为只包含变量yit非预期成分的条件波动率:
其中,yit∈Rt,Ft,而Rt和Ft分别表示经济和金融层面的变量信息集,E[•|It]表示基于t时期预测信息集It的条件期望。具体地,预测信息集It由Xt=(X1t,…,XNt)构成。因此,条件期望E[•|It]和yit+n的值可以通过高维因子模型和扩散指数预测进行估计:
其中,Xit为预测信息集,ft为潜在的共同因子,表示系数矩阵,表示误差项。对于式(29)而言,yjt为每个经济或金融变量序列。为了控制非线性效应,模型中同时控制了共同因子ft的平方项kt,为预测误差。以及(L)分别为滞后L期的系数矩阵的有限多项式,在此,本文选取滞后期L=6 进行估计。随后,通过对经济变量和金融变量的非预期条件波动率(n)进行等权平均(wj=1/Ny)加总,即可构建经济不确定性指数和金融不确定性指数:
根据上述内容不难发现,不确定性指数的合成方法在考虑变量波动时剔除了相应的预期成分。事实上,这种测度方式与理论模型中不确定性τ的构造(即“技能缺口” 的方差)在本质上完全一致,进而有效地实现了理论模型与实证数据的有机衔接。
(二)数据选择与处理
对于经济不确定性与金融不确定性的测度,本文参考黄卓等(2018)以及赵文佳和梁燚焱(2020)的指标构成,选取90 维经济变量信息集(Rt),170 维金融变量信息集(Ft),以及291 维预测变量信息集(Xt)(见表1)。其中,预测变量信息除包括经济变量信息集和金融变量信息集外,还包括31 维经济政策变量信息集。本文所使用的变量选用2002 年1 月至2022 年9 月间的月度数据。不确定性指数的原始变量数据来源于中经网统计数据库、Wind 数据库以及锐思数据库。

表1 中国经济不确定性与金融不确定性的指标构建
就数据处理而言,本文首先对上述291 维预测变量信息集中的274 维中国经济金融变量进行了新年效应处理,使得各变量从前一年12 月至当年1 月的增长率等于当年1 月至2 月的增长率。其次,对产出、消费以及投资等具有趋势性的变量进行了物价平减和X-12 季节调整,消除了价格因素和季节因素。再次,为了满足时间序列的平稳性要求,本文基于单位根检验结果,对非平稳变量进行一阶差分处理后转换为平稳序列。最后,为了消除量纲的影响,本文对所有序列均进行标准化处理。
(三)中国经济不确定性与金融不确定性的波动态势分析
在上述不确定性指数构造方法的基础上,考虑到随着预测步长的增加,不确定性的平均水平将逐渐提高,而其变异程度则将有所下降。因此,本文选取预测步长n为6 期(即计算未来6 个月的不确定性指数),以此构建中国经济不确定性与金融不确定性指数。需要说明的是,为了探究不确定性与经济增长的深层次关系,本文对月度频率的不确定性指数进行了加权处理,将其转换为2002 年第一季度至2022 年第三季度的季度不确定性指数,结果如图1 所示。
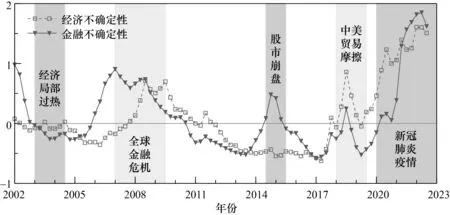
图1 中国经济不确定性与金融不确定性指数
图1 展示出中国经济不确定性与金融不确定性的时变动态,总体而言,经济不确定性与金融不确定性的变动趋势较为一致。其中,不确定性自2002 年开始持续降低,直至2006年附近接近波谷。随后,不确定性日渐增加,于全球金融危机期间达到阶段峰值。伴随着金融危机的结束,不确定性逐渐下降,进而长期处于低水平的震荡区间。2018 年伊始,受中美贸易摩擦深化影响,不确定性呈现出螺旋式上升趋势。此后,叠加新冠肺炎疫情等极端风险事件,不确定性水平屡创新高。
此外,观察经济不确定性与金融不确定性的演化轨迹不难发现,尽管二者的总体波动趋势十分相似,但具体的波动过程不尽相同。例如,2015 年,受中国股票市场剧烈波动影响,金融不确定性水平大幅上升,而同期基于实体经济层面的经济不确定性则无任何明显波动。进一步地,比较二者的波动特征还能够发现,金融不确定性的波动更为频繁、剧烈,并且当经济系统中的不确定性水平出现大幅波动时,金融不确定性的变动通常领先于经济不确定性。这意味着,相较于经济不确定性,金融不确定性能够作为更好的经济预测先行指标,更加敏锐地捕捉经济发展状况的阶段性趋势与动向。
四、不确定性视阈下中国经济风险的确定性识别
为了揭示预期经济增长的时变运行区间,识别不确定性视阈下中国经济风险的波动特征,进而探究经济不确定性与金融不确定性对经济风险的潜在影响,本文拟通过构建基于不确定性条件的预期经济增速分布,从在险增长、相对熵值以及期望损失模型等多维视角,实现对经济风险的有效识别与测度,刻画不确定性冲击下经济风险的确定性规律。
(一)基于在险增长模型的中国经济风险识别
与衡量金融风险的在险价值模型相类似,在险增长模型旨在衡量未来经济增长的风险值。具体地,在险增长采用经济增长概率分布中分位数的值,即预期经济增速分布中不同分位数对应的经济增速水平予以度量。不同风险概率下的在险增长水平(即不同分位数的预期经济增速水平)能够反映不同的经济含义,进而实现对经济风险的有效测度。例如,5%分位数的预期经济增速为a,表示未来经济增速有5%的概率低于a,即有95%的概率高于a;同理,95%分位数的预期经济增速为b,表示未来经济增速有95%的概率低于b。因此,低分位数与高分位数的预期经济增速本质上反映的是,在一定风险(置信)水平下,未来经济增速的下限值与上限值,即经济下行风险与经济上行风险。
为了估计基于不确定性条件的预期经济增速分布,通常需要进行两步计算。第一步是通过分位数回归获取一些重要分位点的回归结果,即估计出预期经济增速分布的部分结果;第二步是将得到的部分回归结果共同映射到偏态t分布中,进而拟合形成完整的预期经济增速分布。因此,本文首先构建如下条件分位数回归模型:
其中,xt为解释变量,包括常数项、当期实际经济增速①本文选取2002 第一季度至2022 第三季度的GDP 同比实际增速作为当期实际经济增速。(控制变量)以及不确定性指数。为辨析中国经济不确定性和金融不确定性对预期经济增速分布的异质性影响,本文分别以经济不确定性和金融不确定性为条件变量构建分位数回归模型。yqt+m为未来m期的预期经济增速,具体可划分为不同的分位数q。δq为系数矩阵,其行和列分别表示不同分位数和不同解释变量的回归系数。m为预测期数,本文采用季度数据,选取预测期m=4(即四个季度),以期探究不确定性冲击的潜在影响。在分位数回归模型中,δq的估计值应使得残差的分位数加权绝对值最小:
其中,Π(•)为指示函数,若括号内逻辑关系成立,指示函数为1,反之则为0。式(32)使得残差绝对值能够根据残差项的大小被赋予不同权重。由此,可以得到xt对yt+m的条件分位数:
1.预期经济增速与不确定性的相关性检验
为了直观地刻画不同分位数预期经济增速与不确定性的关系,本文初步描绘了预期经济增速与不确定性的散点图。进一步地,运用条件分位数回归模型分别拟合出5%、50% (即中位数)以及95%分位数预期经济增速对不确定性的回归拟合直线。此外,为了与不同分位数的拟合直线进行对比,本文还刻画了预期经济增速对不确定性的OLS 估计结果。其中,图2 展示出预期经济增速与经济不确定性的散点图,图3 绘制出预期经济增速与金融不确定性的散点图。
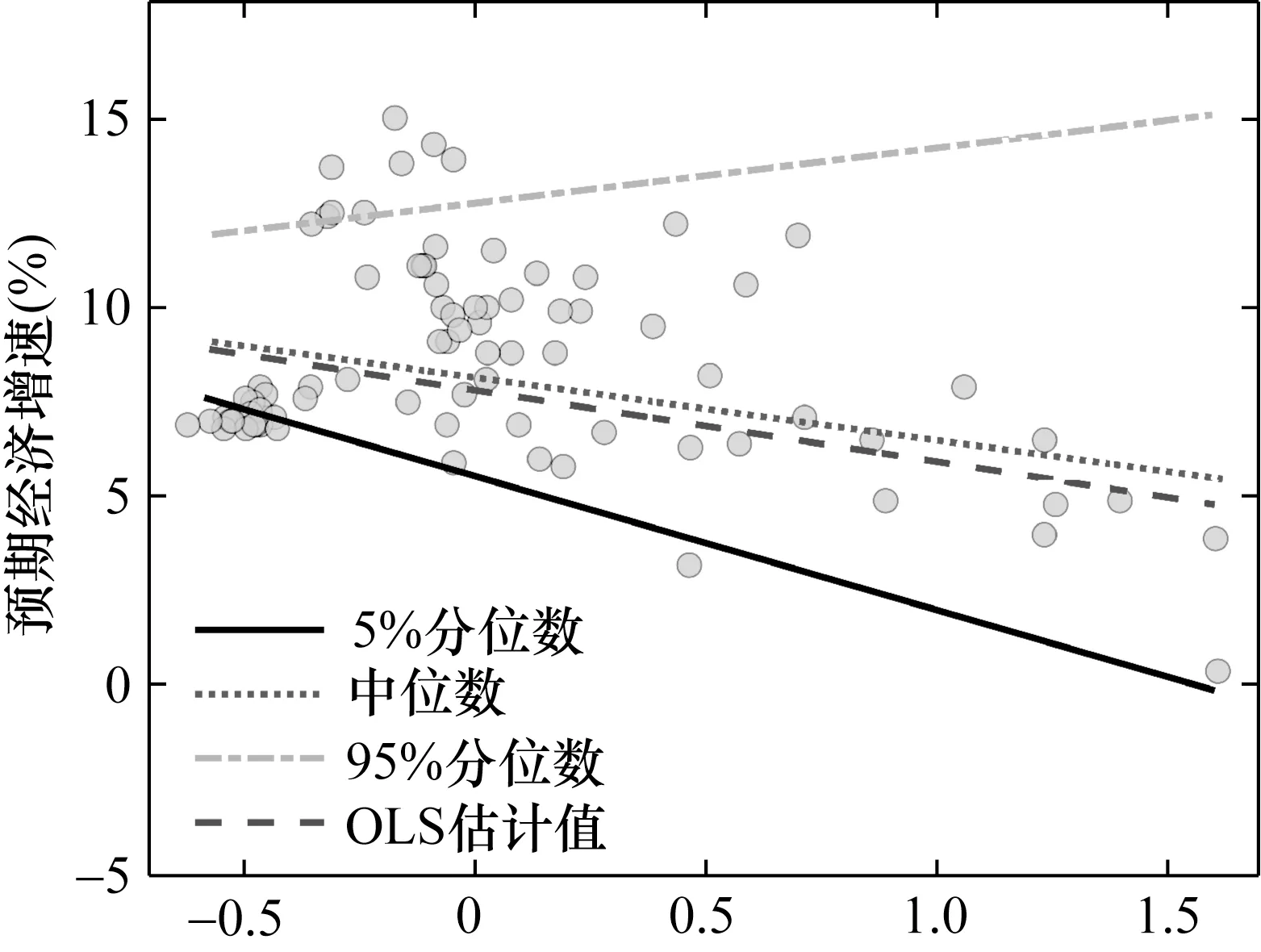
图2 预期经济增速与经济不确定性散点图
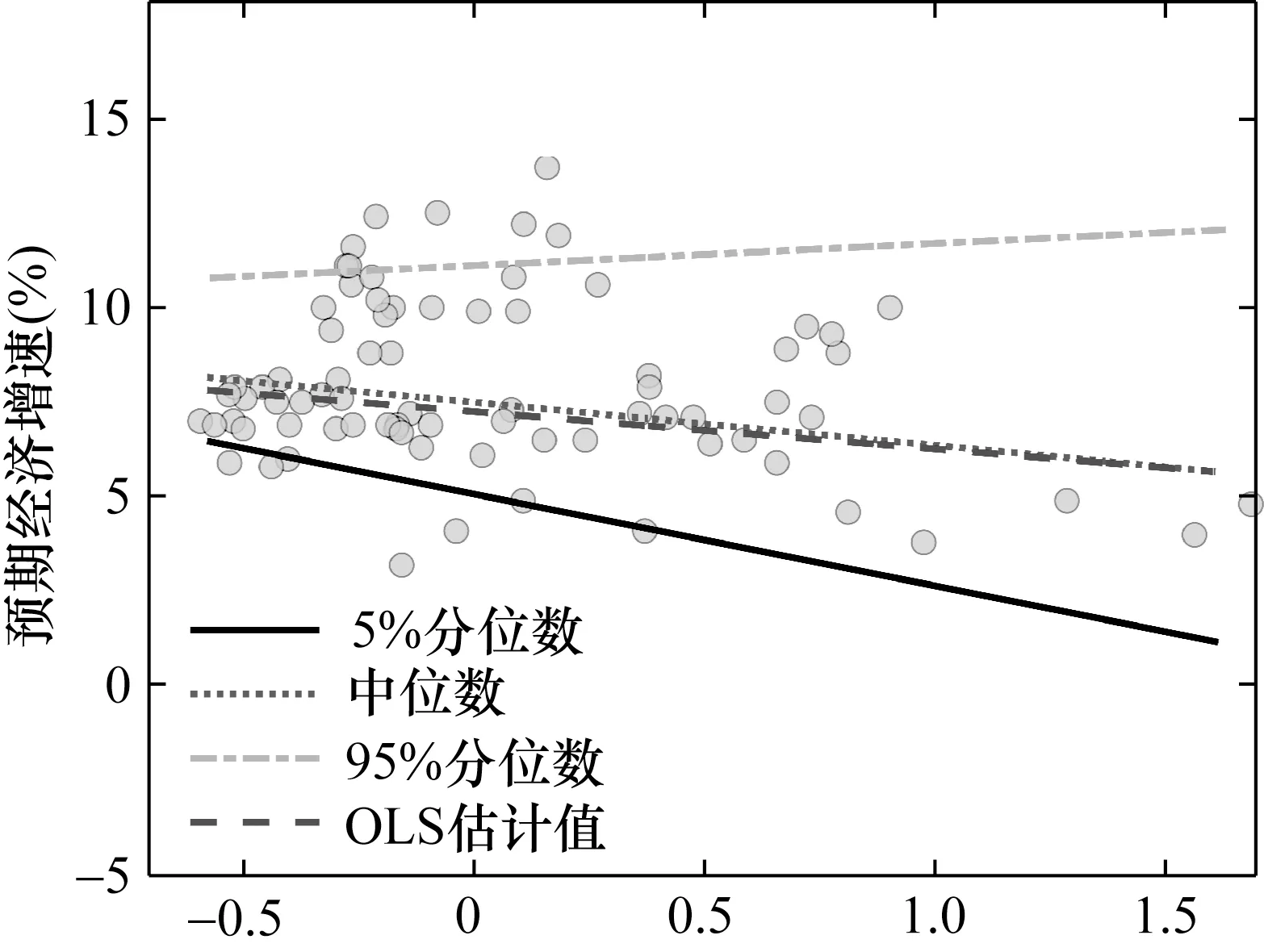
图3 预期经济增速与金融不确定性散点图
观察图2 与图3 不难发现,一方面,预期经济增速对经济不确定性与金融不确定性的回归拟合直线具有明显的共性特征。具体而言,95%分位数预期经济增速的回归斜率显著为正,而5%分位数、中位数以及OLS 回归的拟合斜率则显著为负。这意味着,不同分位数预期经济增速与不确定性的相关关系明显不同。其中,不确定性的升高使得高分位数的预期经济增速有所增加,同时引致低分位数的预期经济增速不断下滑。另一方面,基于经济不确定性与金融不确定性的回归拟合结果存在显著的异质性特征。从5%分位数、中位数以及95%分位数预期经济增速的回归斜率来看,相较于金融不确定性,经济不确定性的影响相对更大。这表明,经济不确定性能够更为显著地升高预期经济增速的上限值,同时还可以更为明显地降低预期经济增速的下限值。此外,从预期经济增速对不确定性的OLS 估计结果来看,经济不确定性的负向影响同样更为显著。因此,可以判断,与金融不确定性相比,经济不确定性的经济效应明显较大,能够造成更为剧烈的经济波动。
2.预期经济增速的分位数回归估计
根据条件分位数回归模型,本文能够进一步估计出预期经济增速对当期经济增速和不确定性的回归系数。图4 与图5 分别展示出基于经济不确定性与金融不确定性条件的分位数回归结果。具体而言,图4(a)与图5(a)描绘了当期经济增速对预期经济增速的影响,图4(b)与图5(b)刻画了不确定性对预期经济增速的影响。其中,X轴表示不同分位数,Y轴为分位数回归的系数估计结果,OLS 估计值反映解释变量对预期经济增速均值的回归系数结果,深色阴影部分面积为系数估计结果的置信区间。①图中阴影面积为零假设的95%置信区间,零假设假定不确定性与经济增长之间符合线性关系。特别地,本文使用不确定性和实际经济增速的全样本演化来估计具有四阶滞后、高斯分布和一个常数的向量自回归(VAR),并利用1 000 个样本进行bootstrap 计算不同置信水平下的边界。
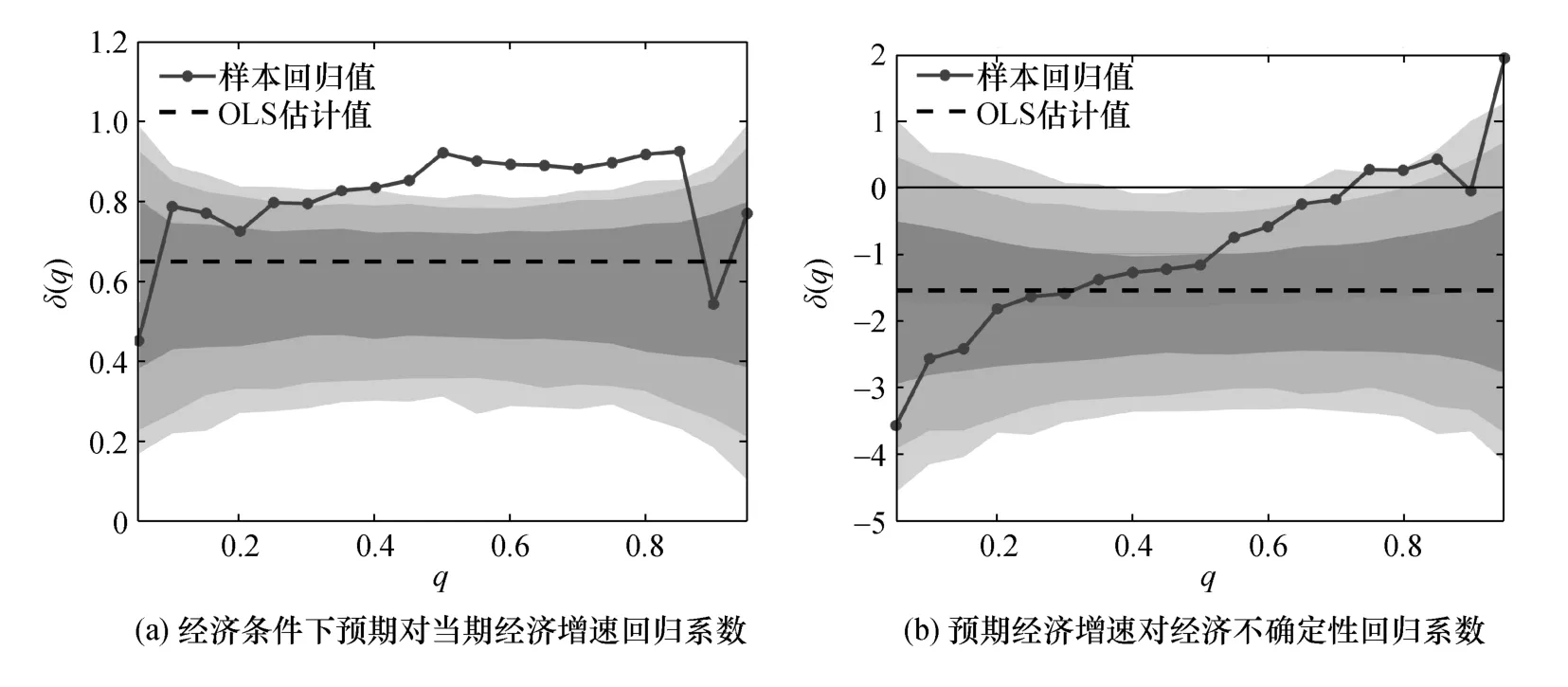
图4 基于经济不确定性条件的分位数回归系数结果

图5 基于金融不确定性条件的分位数回归系数结果
观察图4(a)与图5(a)中的样本回归系数能够发现,无论是以经济不确定性还是金融不确定性为条件变量,当期经济增速对不同分位数预期经济增速的影响均较为稳定,始终围绕在0.6 的回归系数值附近。形成鲜明对比的是,根据图4(b)与图5(b)可知,低分位数至高分位数向上倾斜的回归系数走势表明,与高分位数的预期经济增速相比较,不确定性对低分位数预期经济增速具有更大的负向作用。这意味着,不确定性对经济风险具有明显的非对称性影响。其中,不确定性能够对未来经济增速的下限值产生更为显著的负向冲击,从而引致更大的经济下行风险。
对比图4(b)与图5(b)的样本回归系数不难看出,经济不确定性对低分位数预期经济增速的回归系数接近-4,约是金融不确定性影响系数的二倍。这表明,相较于金融不确定性,经济不确定性能够对未来经济增速的下限值产生更强的驱动力,致使经济潜存更大的下行风险。此外,从图中的OLS 估计值来看,经济不确定性对预期经济增速均值的负向影响同样更为剧烈。追根溯源,经济不确定性能够通过实物期权效应和风险规避效应,对经济主体的投资与消费意愿产生明显的抑制作用,从而对宏观基本面的投资、消费、进出口以及就业等方面造成显著的负面冲击,引致经济增速迅速下降。同时,经济增速的下降与经济不确定性的增加之间还存在着明显的“自我强化” 机制,即经济不确定性的提高会导致经济增速的下降,而经济增速下降又会反过来进一步推升经济不确定性,从而造成经济不确定性对经济增速的二次冲击,由此加剧经济不确定性的负向影响。就金融不确定性对经济增速的影响而言,一方面,根据金融摩擦机制,金融不确定性能够显著降低金融部门的风险承担能力以及风险承担意愿,进而通过融资风险溢价的波动对信贷规模造成负向影响,冲击企业层面的生产经营,最终导致经济活动相应收缩;另一方面,金融不确定性可以通过金融市场传导至实体经济层面,推动经济不确定性水平的提高,继而间接影响经济增速变动。因此,分析上述影响机制可以发现,经济不确定性与经济增速更为密切相关,能够对经济增速产生更加显著的负向冲击。
3.基于在险增长模型的中国经济风险走势判断
正如前文所述,不确定性对经济风险具有明显的非对称影响。那么,经济上行及下行风险是否会因此呈现出相似的非对称性特征? 鉴于此,本文基于在险增长模型,在图6 与图7 中分别描绘经济不确定性与金融不确定性条件下预期经济增速的时变走势,从而直观地体现中国经济风险的波动路径。图中虚线(即阴影部分边缘)从下至上分别刻画了预期经济增速的条件5%、10%、25%、75%、90%以及95%分位数走势,实线描绘了预期经济增速的条件中位数走势。

图6 经济不确定性条件下预期经济增速走势

图7 金融不确定性条件下预期经济增速走势
观察图6 能够发现,不同分位数预期经济增速的总体趋势基本一致,但是波动幅度明显不同。具体而言,在全球金融危机以及新冠肺炎疫情期间,低分位数的预期经济增速出现了巨幅下跌,而高分位数预期经济增速则仅呈现相应的微幅下降。此外,在中美贸易摩擦期间,低分位数的预期经济增速快速滑落至零水平附近,而高分位数的预期经济增速却表现出较小幅度的上涨。从图7 可以看出,金融不确定性与经济不确定性条件下的预期经济增速走势总体上较为相似;不同的是,基于金融不确定性条件的预期经济增速除了在全球金融危机、中美贸易摩擦以及新冠肺炎疫情期间呈现显著的非对称波动,还对2015 年的股市崩盘产生了明显响应。彼时,低分位数的预期经济增速大幅下降,接近金融危机时期的极低水平,而高分位数预期经济增速则表现出不同程度的意外上升。
综观图6 与图7 不难发现,预期经济增速分布走势呈现出明显的非对称性特征,即低分位数的预期经济增速随着时间的推移变动异常剧烈,而高分位数的预期经济增速则相对平稳,并且当经济处于极端风险阶段时,这种非对称性特征更为明显。事实上,这完全可以根据图4(b)与图5(b)中的分位数回归结果予以解释,即不确定性能够对低分位数的预期经济增速产生更为显著的负向影响。因此,这意味着,伴随着不确定性水平的升高,经济上行及下行风险会呈现出异质性的响应过程,致使经济风险具有明显的非对称性特征。并且,当经济步入风险阶段时,剧烈增加的不确定性会驱使非对称性特征更为显著。需要注意的是,从中美贸易摩擦以及股市崩盘的时点来看,伴随着低分位数预期经济增速的大幅降低,高分位数预期经济增速还可能出现小幅上涨。这意味着,不确定性冲击在显著降低未来经济增速下限值的同时,还可能引致经济增速的上限值微幅上升,这同样与前文中不确定性对部分高分位数预期经济增速的回归系数为正的结果相符。究其原因,不确定性冲击一方面可以抑制经济行为主体的投资和消费意愿,另一方面还可以激发企业层面探索性研究的创新活力,从而产生促进经济发展的增长期权效应。因此,不确定性可能兼具正向影响和负向影响,能够对经济增长产生极为复杂的交互作用,进而引致不同分位数预期经济增速的异质性响应。此外,对比图6 与图7 可知,基于经济不确定性条件的低分位数预期经济增速波动得更为剧烈。例如,2020 年新冠肺炎疫情期间,基于经济不确定性的低分位数预期经济增速大幅降至-10%,而基于金融不确定性的低分位数预期经济增速则保持在-5%的水平附近。这进一步印证了经济不确定性与金融不确定性对经济风险的异质性影响,即经济不确定性能够引致更大的经济下行风险,致使经济表现出更为悲观的增速预期。
(二)中国经济风险中的确定性特征识别
基于在险增长模型的结果表明,不确定性对经济风险具有明显的非对称影响。其中,伴随着不确定性水平的升高,经济下行风险显著增加,而经济上行风险则较为稳定,从而致使经济风险表现出明显的非对称性特征。然而,在险增长模型仅是基于未来经济增长风险值的视角,实现对经济风险的衡量。事实上,经济风险还可以利用预期经济增速分布尾部区域的脆弱性进行测度。因此,本文将根据分位数回归结果,拟合形成完整的预期经济增速分布,以期进一步量化经济上行及下行风险,继而识别不确定性冲击下经济风险的确定性特征,具体过程如下。
首先,将分位数回归得到的系数矩阵代入式(33),可以得到分位数的近似估计和累积分布函数。此后,为使用概率密度函数拟合分位数回归的估计结果,本文引入Azzalini和Capitanio (2003)提出的偏态t分布,其概率密度函数可以表示为:
其中,t(•)和T(•)分别表示偏态t分布的概率密度函数和累积分布函数。偏态t分布包含四个参数,分别为分布的期望μ、标准差ω、偏度η以及自由度υ。事实上,偏态t分布本质上就是在t分布的基础上引入了表示偏度的参数η。当η=0 时,偏态t分布能够退化为传统t分布;当η=0 且υ=∞时,偏态t分布可以进一步退化为正态分布;当η≠0 且υ=∞时,偏态t分布可以转变为偏正态分布。接下来,令条件分位数xt)与偏态t分布累积分布函数的反函数F-1(q;μ,ω,η,υ)之间的距离平方和最小,能够估计出偏态t分布的四个参数:
1.预期经济增速的时变运行区间刻画
根据估计出的偏态t分布参数,本文可以在图8 与图9 中描绘出基于不确定性条件的时变预期经济增速分布结果。其中,X轴表示预期经济增速,Y轴为时间,Z轴为预期经济增速分布的概率密度函数。不难发现,预期经济增速的分布结果与图6 及图7 中的预期经济增速走势在总体上较为相似。事实上,图8 与图9 能够更为直观地反映未来经济增速的区间变动。其中,经济不确定性条件下的经济增速区间跨度相对较大,并且具有明显的时变特征;而金融不确定性条件下的经济增速区间则相对集中,并且表现出较强的稳定性。
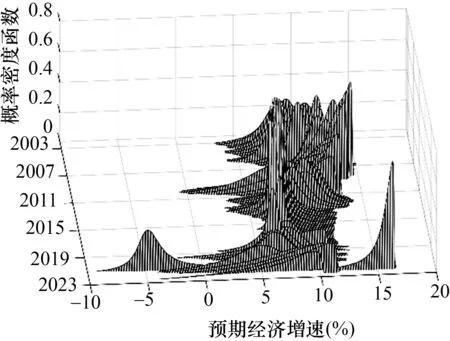
图8 经济不确定性条件下预期经济增速分布

图9 金融不确定性条件下预期经济增速分布
综观图8 与图9 能够发现,经济不确定性与金融不确定性条件下的经济增速区间存在着明显的共性特征。一方面,就时间变化趋势而言,2002 年至2007 年期间,经济增速区间明显右移;而在全球金融危机后,经济增速区间开始缓慢左移,这与中国过去二十年经济增长的阶段转换密切相关,也意味着中国经济已经实现由高速增长阶段转向高质量发展阶段。另一方面,就不同时点上经济增速的区间特征而言,在不确定性较低的繁荣时期(例如2006 年、2012 年),经济增速区间相对较短,经济预期较为确定;在不确定性较高的衰退时期(例如2008 年、2020 年),经济增速区间明显较长,经济预期存在较大的潜在波动空间。显然,这从经验事实的视角进一步印证了不确定性对预期经济增速分布的冲击存在非对称性,表明前文的分位数回归结果具有较强的稳健性。事实上,分位数回归的结果还表明,与金融不确定性相比较,经济不确定性蕴含更多引发经济增速变动的信息,能够对经济增速产生更为强劲的驱动力。这也导致了图8 与图9 的显著差异,即无论从经济增速的区间跨度抑或从概率分布的偏斜程度来看,基于经济不确定性条件的预期经济增速分布的波动都更为剧烈。
2.基于相对熵值和期望损失指标的中国经济风险确定性特征分析
本文运用偏态t分布拟合形成了具体的预期经济增速分布,其中预期经济增速分布即为分别考虑经济不确定性以及金融不确定性的条件经济增速分布。接下来,本文将从预期经济增速分布尾部区域的脆弱性(即不确定性)对预期经济增速分布尾部区域影响程度的视角出发,利用相对熵值和期望损失两种指标,进一步量化经济上行风险与下行风险,从而印证不确定性对经济风险的非对称影响,探析不确定性冲击下经济风险的确定性特征。
相比于无条件经济增速分布,条件经济增速分布给右尾和左尾区域带来的超额概率质量能够有效表征经济上行及下行风险。因此,本文采用gyt+m表示无条件经济增速分布的概率密度函数,表示条件经济增速分布的概率密度函数,根据条件经济增速分布与无条件增速分布的尾部概率差异,将预期经济增速的上行熵值与下行熵值分别定义为与:
其中,是的累积分布函数,是条件经济增速分布的中位数。事实上,下行熵值衡量的是条件中位数以下条件概率和无条件概率的差异,因此当下行熵值较高时,条件经济增速分布的左尾区域相较于无条件增速分布具有更大概率,经济具有更高的下行风险。类似地,上行熵值衡量的是条件中位数以上条件概率和无条件概率的差异,因此当上行熵值较高时,条件经济增速分布的右尾区域相较于无条件增速分布具有更大概率,经济具有更高的上行风险。
此外,另一种衡量方法是利用期望损失(expected shortfall)模型测算条件经济增速分布尾部区域的平均经济增速,并以此量化经济上行及下行风险。其中,期望损失能够有效测度经济的下行风险,而期望损失的上尾对应值则可以清晰地展现经济的上行风险。具体地,对于一个给定的目标概率π,期望损失及其上尾对应值可被分别定义为SFt+m和LRt+m:
事实上,IMF 明确提出将5%分位数的预期经济增速定义为在险经济增长率(以下简称“在险增长率”),并以此衡量经济的下行风险(IMF,2017)。因此,在尾部风险的置信水平选择上,为了与在险增长率的定义相匹配,本文将期望损失模型的目标概率设定为5%。此外,比较期望损失和相对熵值的定义能够发现,尽管这两种方式均衡量了预期经济增速的上行及下行风险,但是期望损失和相对熵值测度的信息含量明显不同。其中,期望损失及其上尾对应值仅从条件经济增速分布的视角刻画了绝对尾部行为;而相对熵值则综合考虑了条件和无条件两种经济增速分布,描绘了条件经济增速分布与无条件经济增速分布的尾部概率差异,即相对尾部行为。
在描述了经济风险的衡量方法后,本文在图10 中分别利用相对熵值和期望损失指标,清晰地量化了经济不确定性与金融不确定性条件下的经济上行及下行风险。其中,图10(a)与图10(b)描绘了预期经济增速上行熵值和下行熵值的动态轨迹,图10(c)与图10(d)刻画了期望损失及其上尾对应值的时变波动。综观图10,尽管相对熵值和期望损失两种指标在度量经济风险时存在一定的信息差异,但是却展现出极为相似的预测结果。
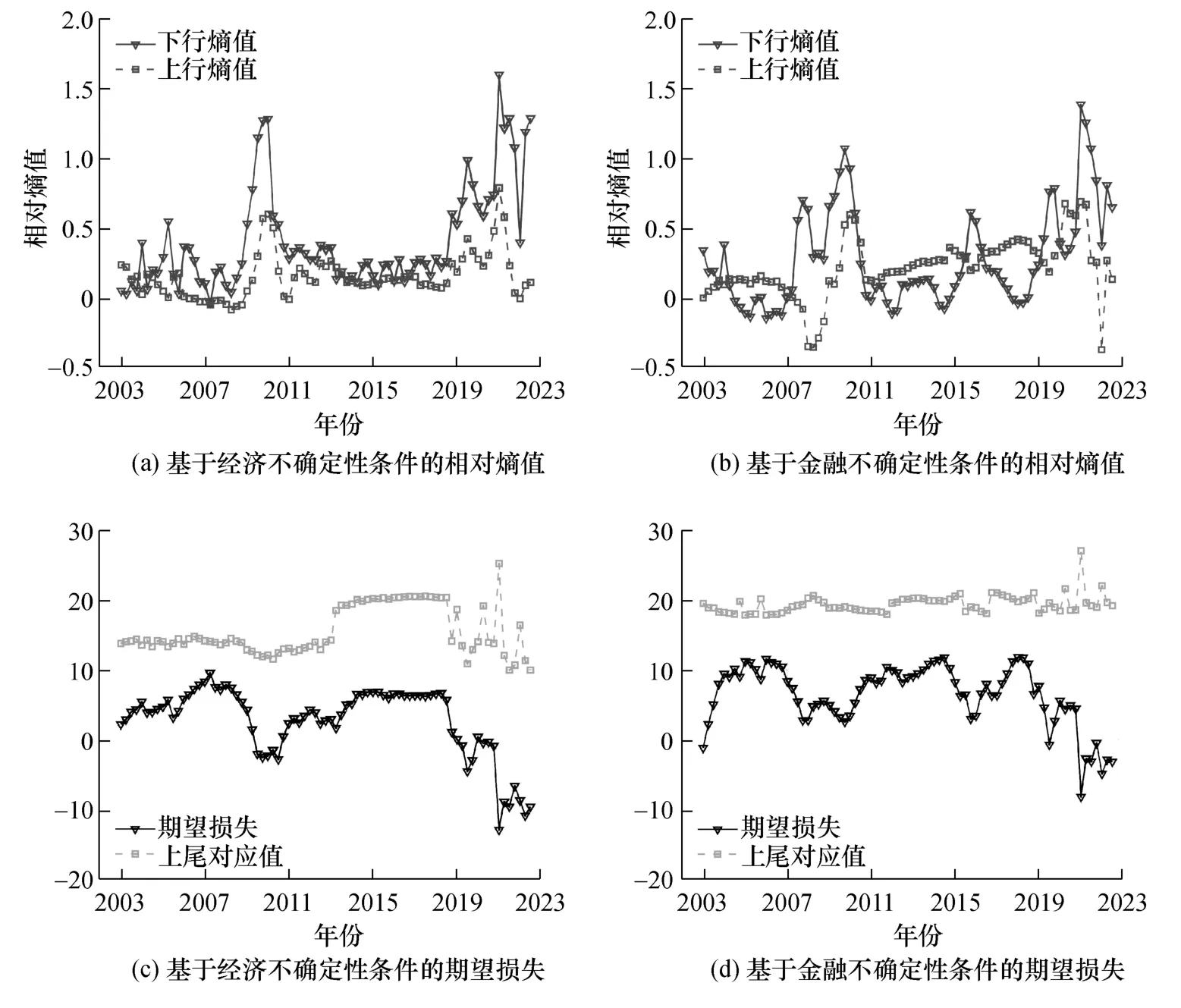
图10 基于相对熵值和期望损失指标的经济风险走势
一方面,观察图10(a)与图10(b)不难看出,预期经济增速的上行熵值与下行熵值均呈现出明显的波动态势。其中,在全球金融危机以及新冠肺炎疫情期间(2008 年以及2020 年),下行熵值大幅增加继而显著高于上行熵值。这表明,与无条件经济增速分布相比,预期经济增速分布的左尾具有更大的概率质量,意味着不确定性冲击使得经济具有更高的下行风险。这与前文强调的不确定性能够造成非对称影响的结论一致,进一步说明了不确定性冲击中的确定性特征。需要注意的是,下行熵值在2010 年以后迅速降低,追根溯源,金融危机时期,为应对经济增速快速回落以及出口负增长等严峻形势,中国通过扩大政府投资和银行信贷等方式,采取了一系列大规模的刺激政策,旨在保障经济平稳较快增长,这些宏观调控举措使得预期经济增速的下行熵值显著下降,最终接近于同期的上行熵值。类似地,2020 年后,伴随着新冠肺炎疫情形势的逐渐好转,下行熵值同样表现出快速下降的波动趋势。这表明,中国经济具有较好的恢复能力,能够从新冠肺炎疫情的泥淖中迅速复苏,意味着中国具有较强的经济韧性与发展潜力。
另一方面,观察图10(c)与图10(d)能够发现,期望损失和上尾对应值的波动路径,与图6 及图7 中低分位数和高分位数预期经济增速的动态轨迹较为相似。具体而言,期望损失及其上尾对应值同时呈现出明显的波动态势,但是,期望损失的波动显然更为剧烈。例如,在全球金融危机、中美贸易摩擦以及新冠肺炎疫情等极端事件期间,期望损失表现出大幅下降的态势,而上尾对应值则仅有相应的微幅震荡。上述发现意味着,预期经济增速分布的尾部风险存在着显著差异,与经济上行风险相比较,经济下行风险相对更大,波动也更为剧烈。因此,综观相对熵值与期望损失的模型测度结果能够发现,不确定性冲击对经济风险具有明显的非对称影响,伴随着不确定性的升高,经济下行风险显著增加,而经济上行风险则明显较为稳定。这与在险增长模型中低分位数和高分位数预期经济增速走势的非对称性特征相呼应,继而有效印证了不确定性冲击下经济风险的确定性特征。
此外,综观图10 能够发现,无论是从相对熵值还是期望损失来看,经济不确定性均具有更为明显的下行驱动作用。一方面,就相对熵值而言,在全球金融危机、中美贸易摩擦以及新冠肺炎疫情期间,基于经济不确定性条件的下行熵值的波峰始终相对更高。另一方面,就期望损失而言,在上述极端风险事件期间,基于经济不确定性条件的期望损失的波动幅度同样更为剧烈,例如,新冠肺炎疫情时期,经济不确定性条件下的期望损失大幅降低(-13%),而金融不确定性条件下的期望损失最终停留在相对较高的增速水平(-9%)。因此,本文从经济风险的多维度视角,进一步展示了经济不确定性与金融不确定性影响的异质性。需要注意的是,观察经济风险指标的时变走势不难看出,尽管目前经济下行风险水平已从峰值回落,但中国仍处于不确定性较高的发展阶段,潜存一定的经济下行风险。
五、中国经济风险的时变路径识别与驱动机制分析
本文基于在险增长模型,描绘了预期经济增速的分布特征,刻画了不确定性对经济风险的非对称影响;随后又利用相对熵值、期望损失等测度方法,进一步印证了不确定性冲击下经济风险的确定性特征。然而,前文仅从经济风险的识别视角,揭示了不确定性视阈下经济风险的波动特征,并未对不确定性冲击的动态影响进行深入探究。因此,为了实现不确定性冲击下经济风险的时变路径识别与驱动机制分析,本文将综合考量经验证据和理论模型的预期结果,以期对不确定性的冲击效应进行系统性分析。
为了将经验证据与理论模型相匹配,我们选取季节调整后的实际GDP 季度值以及未经过标准化处理的季度不确定性指数进行研究。需要说明的是,为了便于敏锐地捕捉不确定性对经济增速的动态影响,本文根据理论分析中预期经济增速的定义gt+1=lnyt+1-lnyt,采用环比经济增速作为经济增速指标。具体地,本文首先计算实际GDP 季度值的迭代变化得到环比经济增速,随后又对环比经济增速进行年化处理,最终采用年化环比经济增速指标展开进一步研究。①本部分的预期经济增速为采用实际GDP 季度值计算得到的季度年化环比增长率。
(一)不确定性的经济增长效应分析
为了探究不确定性的经济增长效应,验证理论分析中不确定性对经济增速均值、波动率等分布特征的影响,本文分别在图11 和图12 中展示经济不确定性和金融不确定性与经济增速特征的相关性。其中,经济增速的分布特征由经济增长率及其高阶矩构成,具体以八期滚动窗测算的经济平均增速、经济增速波动率以及经济增速分布偏度三方面度量。
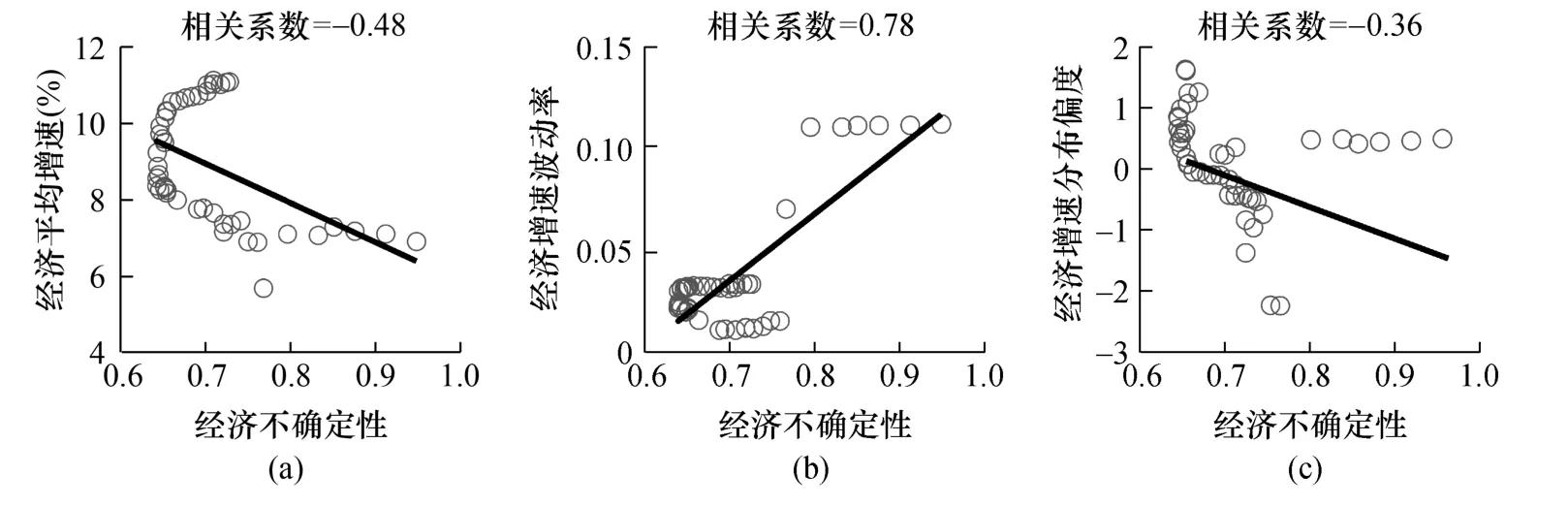
图11 经济不确定性与经济增速特征的相关性

图12 金融不确定性与经济增速特征的相关性
综观图11 与图12 不难看出,经济不确定性与金融不确定性对经济增速分布特征的影响较为一致。首先,观察图11(a)与图12(a)可知,不确定性与经济平均增速呈现明显的负相关关系。这是由于,无论是经济不确定性还是金融不确定性,在微观层面均会影响居民的资产配置及企业投资,而在宏观层面又会导致产出和消费的明显下降,弱化宏观经济政策的调控效果,即不确定性能够引致经济活动减缓,从而使经济增长产生收缩效应。其次,根据图11(b)与图12(b)可知,不确定性与经济增速波动率的相关系数显著为正。事实上,不确定性的增加能够导致经济增速分布的方差(即波动率)显著上升,致使经济增速具有更大的波动空间,而经济增速的波动会再度反馈至不确定性,形成明显的动态交互效应,进而使得不确定性与增速波动率具有高度的相关性。最后,由图11(c)与图12(c)可知,不确定性与经济增速分布偏度具有负相关关系,表明不确定性会导致经济增长概率分布曲线趋于负向偏斜,从而引致更大的经济下行空间。有鉴于此,本文从经验证据的视角印证了理论分析中不确定性对经济增速相关特征的影响,即不确定性的增加会导致经济平均增速明显下降,引发经济增速剧烈波动,并促使经济增长概率分布负向偏斜。
对比图11 和图12 所示的相关系数能够发现,经济不确定性和金融不确定性与经济增速分布特征的相关性存在一定差异。其中,无论是就经济平均增速、经济增速波动率还是经济增速分布偏度而言,经济增速分布特征与经济不确定性的相关系数均明显更大。这意味着,与金融不确定性相比,经济不确定性能够引致更为显著的经济下行风险。究其原因,金融不确定性作为经济景气预测的先行指标,能够更为灵敏地捕捉经济波动,而经济不确定性更多表现为宏观经济波动的同步指标。因此,当经济不确定性显著升高时,实体经济层面势必呈现出明显的实质性波动,即经济不确定性对经济增速分布的影响相对更大。鉴于此,本文在印证理论分析中不确定性影响经济增长分布特征的同时,也进一步说明相较于金融不确定性,经济不确定性对于经济风险的影响更为显著。
(二)不确定性对中国经济风险的时变冲击路径识别
在初步验证不确定性的经济增长效应后,本文将从理论分析与经验证据两个视角刻画不确定性对中国经济风险的时变冲击路径。其中,对于在险增长模型中的预期经济增速分布而言,不确定性对经济风险的冲击路径可以从以下两个方面进行深入探讨:一是不确定性对预期经济增速分布的时变冲击效应,二是不确定性对预期经济增速分布的实际冲击效应。
1.不确定性对预期经济增速分布的时变冲击效应分析
一方面,根据理论模型中的构造,σ2为刻画不确定性的唯一参数。因此,为便于计算不确定性对预期经济增速分布的冲击效应,本文首先设定σ=1。现有文献中的常见取值,如王立勇和徐晓莉(2018),将中国的效用贴现率β设为0.98。接下来,根据式(12),改变σ值使得不确定性τ增加10%①根据不确定性指数的实际数据,不确定性增加1 单位标准偏差冲击对应于不确定性τ 增加10%。,以期得到不确定性对预期经济增速分布冲击的理论预期结果。另一方面,利用不确定性指数与经济增速数据,可以构建如式(31)所示的条件分位数回归模型。需要说明的是,本文根据Jorda(2005)的局部投影估计方法,利用不同预测期m=1,2,…,12 (季度)回归系数的变化路径,表征不确定性冲击对预期经济增速的动态影响。在此基础上,给定经济不确定性与金融不确定性1 单位标准差冲击,即可得到不同分位数预期经济增速的脉冲响应。因此,本文在图13 中描绘出不确定性对预期经济增速分布的冲击路径。其中,图13(a)展示了理论模型预期的脉冲响应结果,图13(b)与图13(c)则分别刻画了经济不确定性与金融不确定性冲击的脉冲响应结果。
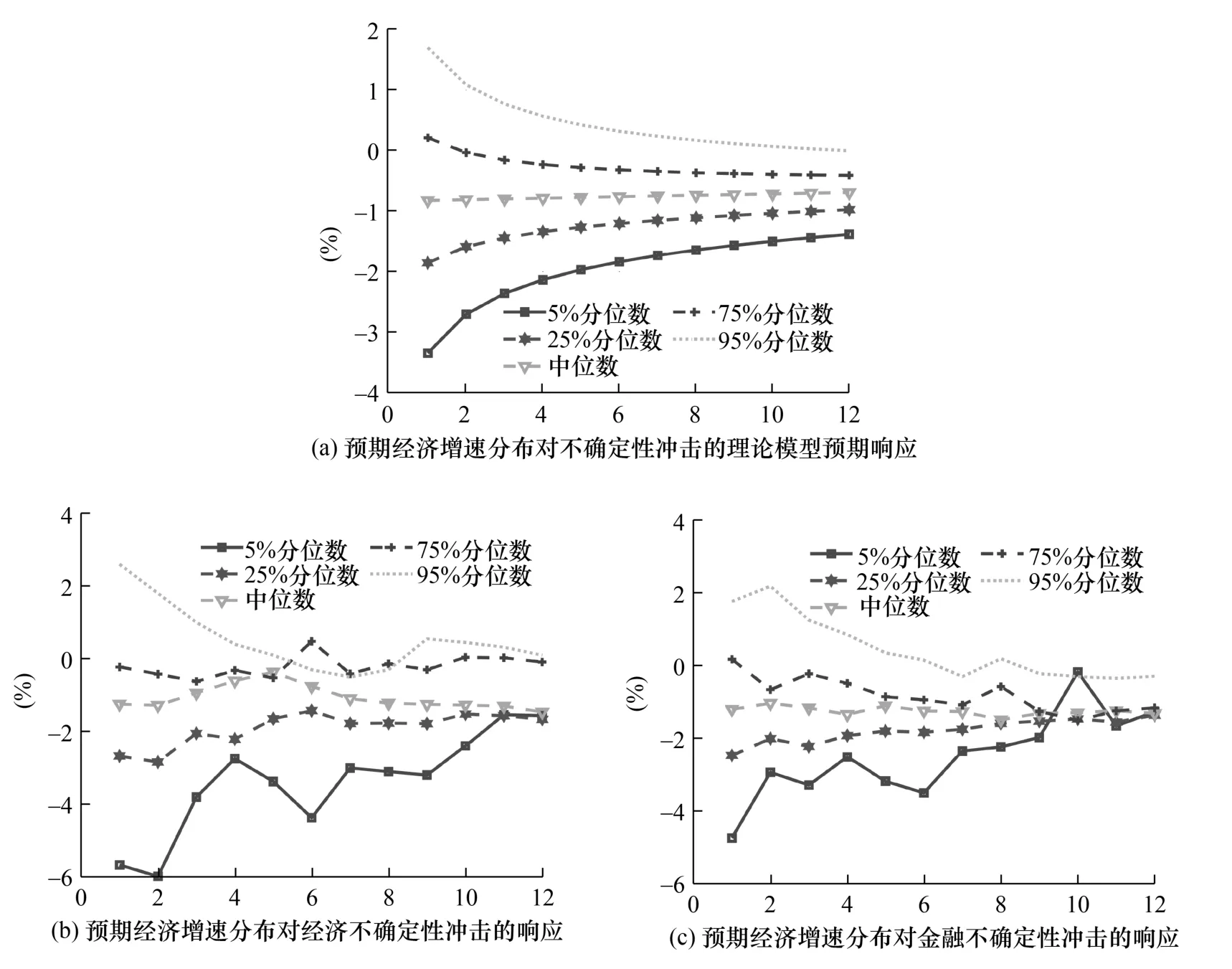
图13 预期经济增速分布对不确定性冲击的脉冲响应轨迹
图13 中理论分析与经验证据的结果一致表明,不确定性对低分位数与高分位数预期经济增速的冲击具有明显的非对称性,这与前文的研究结论完全相符。具体地,就理论模型的预期结果图13(a)而言,不确定性冲击增加1 单位,会立刻引致预期经济增速的5%分位数下降3%,95%分位数上涨2%;就经验证据图13(b)与图13(c)而言,经济不确定性与金融不确定性冲击增加1 单位,会立刻引致预期经济增速的5%分位数下降5%,95%分位数上涨2%。这意味着,不确定性冲击会迅速使得未来经济增速的下限值大幅度下降,经济增速上限值小幅度上升,从而显著增加经济下行风险,同时较小地增加经济上行风险。
比较图13(b)与图13(c)中的脉冲响应轨迹不难发现,经济不确定性与金融不确定性的冲击效应存在着明显差异。一方面,从冲击效应的持续时间来看,经济不确定性的影响周期相对更长。其中,经济不确定性对低分位数预期经济增速的影响存在一定的滞后效应,致使低分位数预期经济增速于第2 期实现最大负向响应。然而,金融不确定性对低分位数预期经济增速的冲击则在第1 期达到峰值,随后,脉冲响应轨迹呈现稳定的收敛趋势。另一方面,从冲击效应的影响程度来看,尽管低分位数预期经济增速对两种不确定性冲击的脉冲响应在第12 期均为-1%,但是经济不确定性对5%分位数预期经济增速的最大冲击接近-6%,而同期(第2 期)金融不确定性冲击仅为-3%,意味着经济不确定性具有更大的下行驱动力。
综上所述,理论模型的预期结果与实际冲击的时变路径在总体上较为相似,表明不确定性冲击下经济风险具有确定性响应路径的同时,也进一步印证了理论分析框架的合理性。根据预期经济增速分布的脉冲轨迹,相比于金融不确定性,经济不确定性冲击不仅持续时间更久,而且影响程度更大,能够引致更大的经济下行风险。此外,理论分析与经验证据的结果还表明,不确定性的冲击效应随着时间的推移逐渐收敛。这意味着,即使没有外生宏观调控政策的对冲,不确定性冲击的负面影响也会逐渐减弱,体现了经济具有恢复增长的内在韧性。但是,12 期(三年)后的冲击效应仍未减弱至零,表明不确定性冲击需要较长的消化周期,能够对经济增长产生长远的负向影响。
2.不确定性对预期经济增速分布的实际冲击效应检验
为了深入探究不确定性对经济风险的实际冲击效应,本文基于预期经济增速分布特征中分散程度以及在险增长率(5%分位数的预期经济增速)的脉冲响应轨迹,揭示不确定性冲击对未来经济增速的区间范围以及经济下行风险的时变影响。进一步地,为了模拟更大规模不确定性冲击的预期影响,本文再度调整理论模型中的参数σ,使得不确定性水平增加20%,继而实现不同规模理论冲击与实证冲击的对比分析,刻画不确定性的实际冲击效应。图14 展示了预期经济增速分布对不同规模不确定性冲击的脉冲响应结果。其中,图14 (a)与图14 (c)描绘了不确定性对预期经济增速分布分散程度的冲击效应,图14 (b)与图14 (d)则刻画了不确定性对在险增长率的冲击效应,虚线表示经济不确定性或金融不确定性增加1 单位标准差冲击后产生的脉冲响应轨迹。需要说明的是,分散程度利用预期经济增速分布的上4 分位数(75%分位数)与下4 分位数(25%分位数)之差,即4 分位距予以衡量。4 分位距将预期经济增速分布的尾部风险值排除在外,能够在反映未来经济增速区间主体范围的同时,更清晰地展现经济增长“期望值”(即未来经济增速预测值)的运行区间。
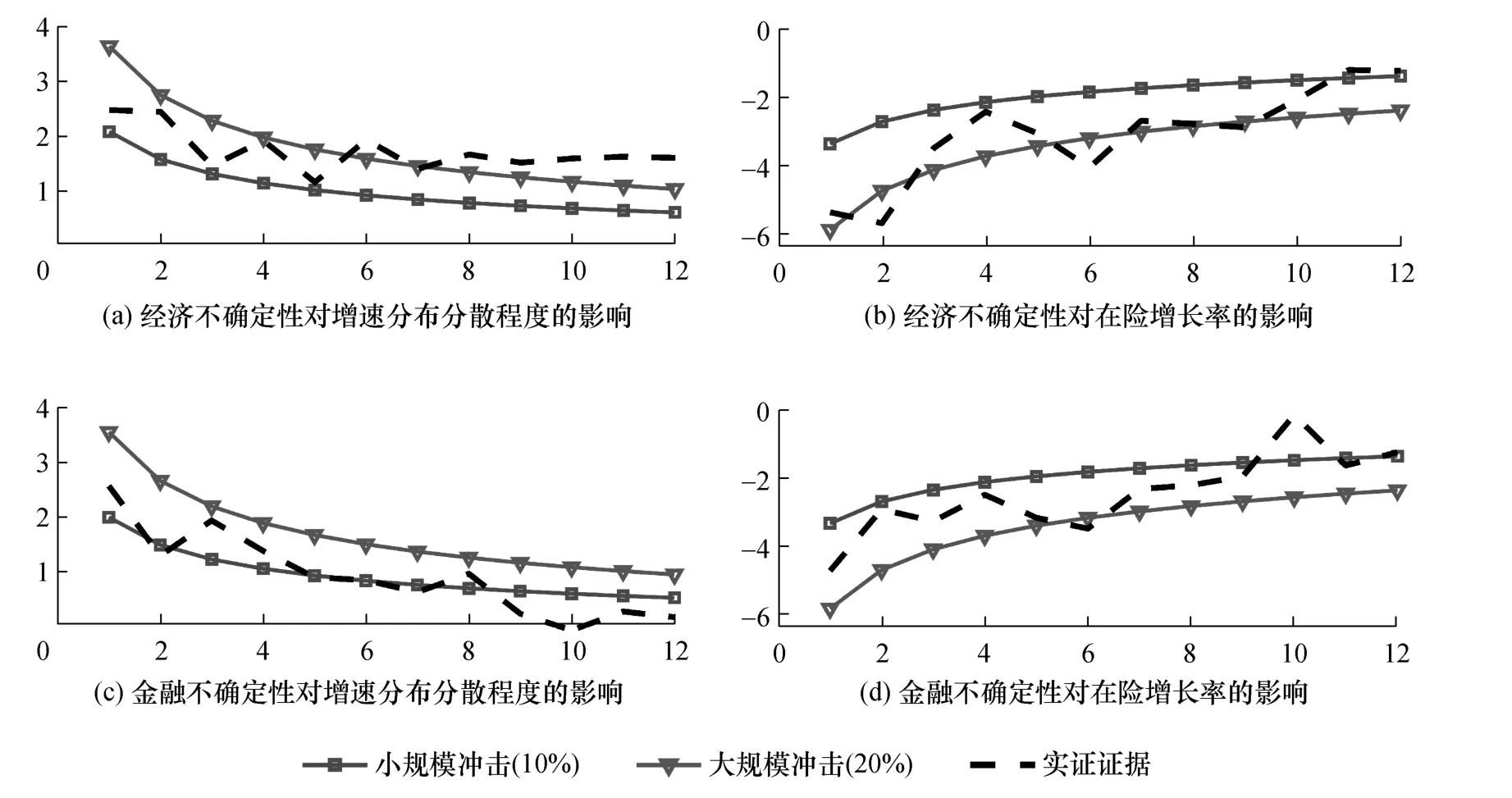
图14 预期经济增速分布对不同规模不确定性冲击的脉冲响应
一方面,就图14 中理论模型的预期结果而言,不确定性增加10%会立刻导致预期经济增速分布的分散程度增加2%,在险增长率下降4%;而不确定性增加20%则会引致分散程度增加4%,在险增长率降低6%。另一方面,就图14 中的实证结果而言,1 单位经济不确定性与金融不确定性冲击能够使得分散程度立刻增加2.5%,在险增长率下降5%。因此,结合图13 中不同分位数预期经济增速对不确定性冲击的脉冲响应轨迹可以判断,不确定性冲击能够引致未来经济增速的运行区间范围迅速扩张。其中,区间上限会小幅下降,而区间下限会大幅降低,这意味着不确定性在驱动经济下行的同时也显著扩大了经济增速的下行空间。
此外,无论是从预期经济增速分布分散程度还是在险增长率的脉冲响应来看,经济不确定性造成的冲击效应都更为剧烈,十分接近大规模冲击的影响程度。具体而言,观察图14(a)与图14(c)可知,经济不确定性对分散程度的冲击效应在前两期相等且最大,随后呈现出缓慢的波浪式下降趋势。但是,第7 期后的冲击不再减弱,始终停留在1.5%的水平附近;金融不确定性对分散程度的冲击在第1 期实现最大值后随即收敛,最终减弱至零。这意味着,经济不确定性能够对未来经济增速造成一定规模的永久性冲击,即1 单位经济不确定性冲击会使得经济增速的区间范围扩大1.5%,这也印证了基于经济不确定性条件的预期经济增速更为分散的分布特征。类似地,比较图14(b)与图14(d)可以发现,经济不确定性对在险增长率的冲击效应始终围绕在大规模冲击附近,而金融不确定性对在险增长率的影响相对较小且衰减较快。因此,本文从预期经济增速分布特征的视角,进一步说明了经济不确定性冲击的影响程度更大、持续时间更久。
需要注意的是,比较图14 中实证数据与理论模拟的脉冲结果不难发现,无论是就经济不确定性还是金融不确定性而言,不确定性的实际冲击效应均介于理论模型预期的小规模冲击与大规模冲击之间。这意味着,不确定性对预期经济增速的实际影响明显大于理论分析中同等规模的冲击效应。究其原因,相比于理论模型拟合的预期冲击,不确定性除了能够通过产生恐慌情绪等难以量化的微观渠道放大其实际冲击效应,更为重要的是,在不确定性降低经济增速的同时,经济增速的下降还会引致不确定性水平的进一步增加,即不确定性对经济增长的影响存在“双向反馈” 的动态溢出循环。这使得不确定性冲击在现实情境下表现出更为复杂的经济效应,能够加剧不确定性对经济风险的实际冲击作用。
(三)基于理论框架的中国经济风险驱动机制分析
本文通过综合分析理论模型预期与实证检验的脉冲响应结果,有效揭示了不确定性冲击下经济风险具有确定性的时变响应路径,验证了理论模型构建的合理性。然而,这也衍生出一系列问题:何为“技能缺口”? 为何“技能缺口” 的波动能够定义不确定性?不确定性又如何驱动经济风险?
所谓技能缺口,其在理论模型中等价于企业现有技能组合与最优技能组合之差,而在本质上反映的是经济投入要素(包括劳动和资本投入)无法满足企业技术要求的比例。不难发现,技能缺口充分体现了企业技术水平与投入要素之间的矛盾关系,技能缺口越大,表明企业的技术水平与投入要素越不匹配。从企业的实际生产经营决策来看,技术水平以及投入要素的动态调整,正是企业应对外部环境不确定的内在表现,因此本文利用技能缺口的波动刻画不确定性。事实上,企业动态调整技术以及投入要素这一过程,能够根据企业实际产出与潜在产出的比例波动进行清晰刻画。而在实践中,产能利用率作为总产出对生产设备的比率,可以有效地反映实际产出对潜在产出的比例。有鉴于此,本文将产能利用率与技能缺口联系起来,利用产能利用率的波动对不确定性的概念进行量化,继而从实际生产的视角阐释不确定性的经济含义,分析理论框架中不确定性对经济风险的驱动机制。
图15 展示了产能利用率波动与经济下行风险的相关性。其中,图15(a)描绘了产能利用率波动与经济不确定性条件下在险增长率的相关性,图15(b)则刻画了产能利用率波动与金融不确定性条件下在险增长率的相关性。不难发现,产能利用率波动与在险增长率呈现出明显的负相关关系。究其原因,当经济景气繁荣时,厂商往往过度乐观,盈利能力的提高会强化其对未来看好的预期,厂商会扩大投资并提高产能利用率;一旦经济景气发生逆转,市场需求会迅速下降,此时产能过剩不可避免,进而经济主体产能利用率降低,这在一定程度上会加剧经济波动。因此,产能利用率的大幅波动意味着外部环境具有强烈的不确定性,故与更大的经济下行风险密切相关。
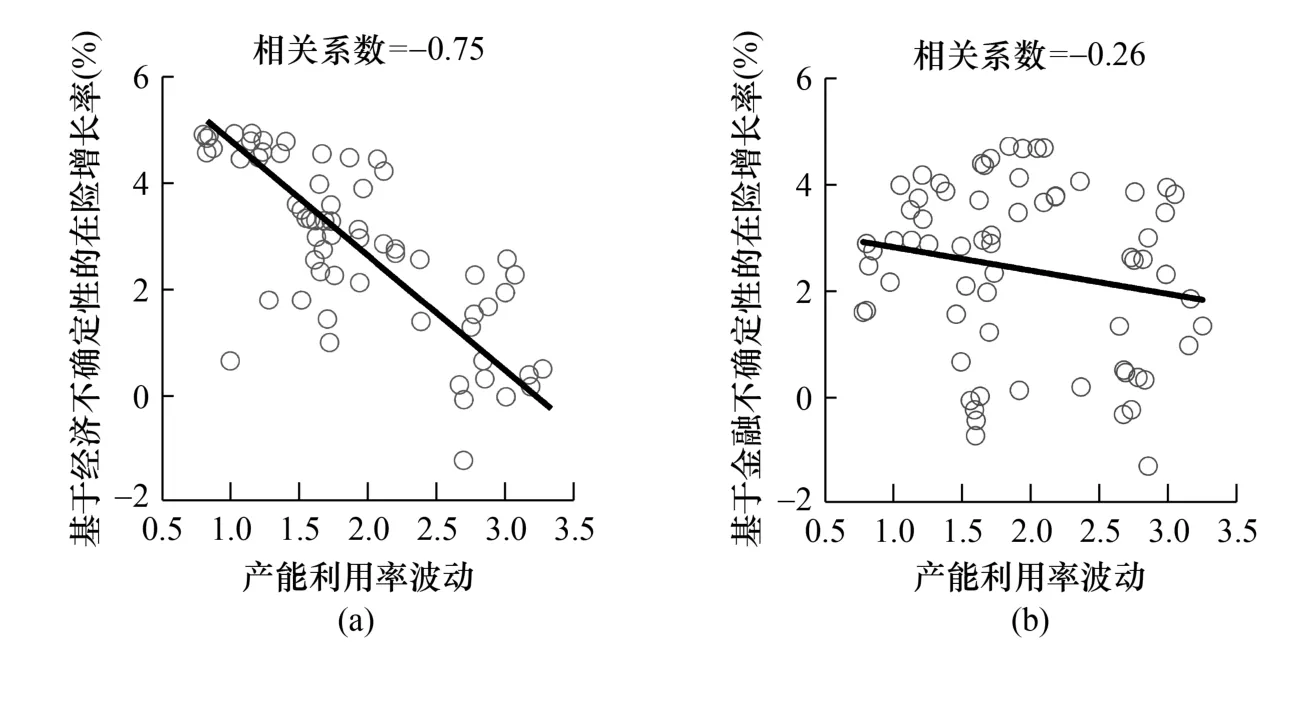
图15 产能利用率波动与经济下行风险的相关性
此外,比较图15(a)与图15(b)可知,与金融不确定性条件下的在险增长率相比,产能利用率波动与经济不确定性条件下的在险增长率相关系数明显更大。追根溯源,产能利用率作为衡量生产部门尤其是第二产业生产经营状况的重要指标,与基于实体经济层面的经济不确定性关系更为密切,而与金融市场的不确定性关联程度则相对较小。因此,产能利用率波动与经济不确定性引致的下行风险相关性更为显著。本文基于产能利用率的视角,运用实际数据刻画了理论框架中技能缺口的概念,继而在分析产能利用率波动与经济下行风险相关性的同时,阐释了内生不确定性的经济含义,进而有效印证了技能缺口—内生不确定性—经济风险的驱动机制。
六、结论与政策启示
首先,本文利用高维因子模型,实现经济不确定性与金融不确定性的分离测度。其次,基于经济增长概率分布的视角,本文将经济增长与不确定性纳入在险增长的统一框架,继而识别不确定性视阈下经济风险的确定性特征。最后,本文综合考量经验证据与理论模型的预期结果,实现不确定性冲击下经济风险的时变路径识别与驱动机制分析。本文得出如下结论。第一,预期经济增速的条件分位数回归结果表明,不确定性对经济风险具有明显的非对称影响。相比于经济上行风险,不确定性对经济下行风险具有更为显著的影响,从而能够引致更大的经济下行风险。随后,基于在险增长、相对熵值以及期望损失等模型的测度结果,有效印证不确定性对经济风险的非对称影响,进一步揭示不确定性冲击下经济风险的确定性特征,即伴随着不确定性的升高,经济下行风险显著增加,而经济上行风险则较为稳定,并且当经济处于不确定性较高的风险阶段时,这种非对称性特征会更加明显。第二,预期经济增速分布的时变路径表明:一方面,就预期经济增速的变化趋势而言,2002 年至2007 年间,经济增速持续升高,而在全球金融危机后,经济增速开始逐渐放缓,证实中国经济已经实现由高速增长阶段转向高质量发展阶段。另一方面,就预期经济增速的区间特征而言,当不确定性较低时,未来经济增速的潜在波动空间相对较小,经济预期较为明确;而当不确定性较高时,未来经济增速通常具有较大的波动空间。这意味着,不确定性冲击不仅能够引致经济增速大幅下降,而且会致使经济增速下行空间显著扩张。第三,从不确定性的时变冲击路径来看,不确定性冲击下的预期经济增速分布呈现出非对称性的脉冲响应轨迹,并且不确定性冲击的消化周期相对较长,能够对经济增长产生长远的负向影响。从不确定性的实际冲击效应来看,经验证据与理论分析的预期结果表明,不确定性对经济增长的实际影响明显大于理论分析中同等规模冲击的冲击效应。这意味着,不确定性对经济增长的影响具有“双向反馈” 的动态溢出循环,使得不确定性在现实情境下表现出更为复杂的经济效应,能够加剧不确定性对经济风险的实际冲击作用。第四,根据预期经济增速的条件分位数回归结果、经济风险的测度指标以及不确定性冲击的脉冲响应轨迹等一系列经验证据,经济不确定性与金融不确定性对经济风险具有明显的异质性影响。其中,无论是就不确定性冲击的影响程度还是持续周期而言,经济不确定性的影响均更为显著。这意味着,与金融不确定性相比较,经济不确定性包含更多引发经济增速波动的信息,能够引致更大的经济下行风险,致使经济表现出悲观的增速预期。
基于上述结论,本文提出如下政策建议:第一,要充分认识不确定性冲击中的确定性规律,重视不确定性对经济风险的非对称冲击效应,选择更具针对性的监管目标和政策工具。当不确定性水平较高时,不仅应当关注未来经济增长的预期值,更要重点监控和防范不确定性冲击引致的巨大经济下行风险,进一步强化风险监管与预期管理,保障经济运行在合理区间。第二,要创新与优化宏观经济调控,将在险增长、相对熵值、期望损失等参考指标纳入宏观调控范畴,健全风险监测预警和早期干预机制,加强宏观经济政策与审慎监管措施的协调配合。第三,在应对不确定性冲击的负面影响时,要加强与经济主体的沟通交流,引入前瞻性指引等政策工具,强化公众的预期管理,避免产生夸大“坏消息”、忽视“好消息” 的市场恐慌情绪。同时,要积极制定和实施宏观调控政策,提高宏观调控有效性,优化完善冲击处理机制,主动防范和化解由不确定性的内生放大机制形成的叠加冲击。第四,考虑到经济不确定性与金融不确定性的同期水平存在显著差异,并且经济不确定性与金融不确定性对经济风险具有明显的异质性影响,监管当局应密切关注经济和金融状况及其不确定性因素,充分意识到金融不确定性的先导性特征,重点关注经济不确定性的剧烈变化,在努力实现“稳增长” 与“防风险” 双重目标的背景下,为经济平稳健康发展营造良好的外部环境。
目前,中国正处于全面贯彻党的二十大精神的关键之年,在这重要的历史节点上,面对纷繁复杂的外部环境,国内经济“稳增长” 承受着空前压力。在此背景下,识别不确定性与经济风险之间的关系,揭示不确定性中的确定性规律,对于国民经济健康发展至关重要。唯有强化风险监管与预期管理,创新宏观经济调控体系,方能防范化解经济金融风险,保持经济运行在合理区间,进而有利于加快构建新发展格局,实现第二个百年奋斗目标,以中国式现代化全面推进中华民族伟大复兴。

