基于正交试验的基坑围护结构优化设计

王栋灿

杭州下沙路隧道有限公司 浙江 杭州 311199

近年来，伴随着城市建设的快速发展，地铁和地下通道等地下空间的建设也得到了快速发展。而基坑围护结构是地下工程建设中不可或缺的一部分，因此设计出一种既安全，又可行、经济的基坑支护方案，是当前迫切需要解决的难题[1]。

1 依托工程及其优化方法

1.1 工程概况

杭州某项目包含5幢高层住宅和4幢多层商用楼，其中一些商用楼位于轨道交通的上部。工程周边场地平整高程为4.00m。地下室底板顶标高0.15m～ 1.2m，基坑开挖深度为4.75m～6.10m。项目需开挖两个基坑，分别为车站东侧基坑和车站西侧基坑，西侧基坑面积较小，约1113m2，采用钻孔灌注桩+三轴搅拌桩+一道组合型钢支撑。东侧基坑面积较大，约13300m2，临近地铁位置采用钻孔灌注桩/双排桩+三轴搅拌桩+一道组合型钢支撑。其余位置采用SMW工法桩+一道组合型钢支撑[2]。计算所需要用到的围护结构、支撑、板的具体参数如表1所示。

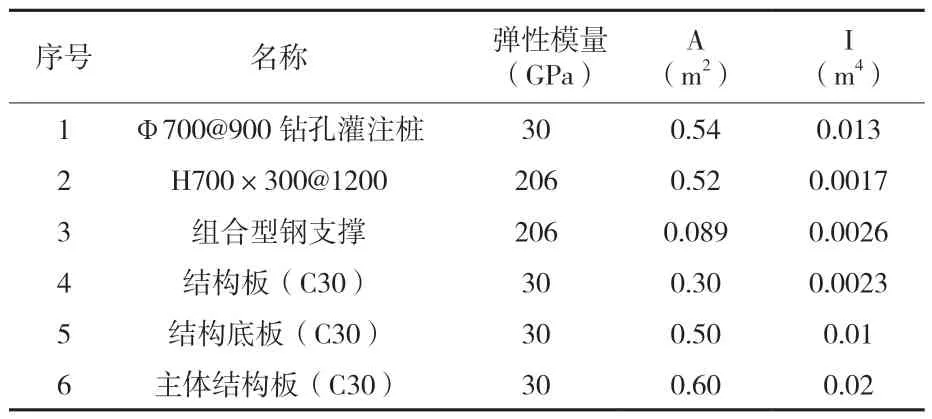
表1 围护结构、支撑、板参数表

1.2 有限元数值模拟

PLAXIS有限元软件的功能主要偏向于岩土工程方向，可以实现岩土工程的数值分析。其中，PLAXIS 2D和PLAXIS3D这两款软件分别对应的是岩土工程专业软件中的PLAXIS2D和PLAXIS3D，这两款软件主要面向岩土工程方向进行数值分析。本文基于杭州市某基坑工程，采用二维有限元数值模拟方法，建立了二维有限元数值模型，通过多组正交试验方案进行了数值模拟计算，对基坑围护结构的位移变形和稳定性进行了分析和探讨，并结合现场监测数据对基坑围护结构的优化设计方案进行了初步探索[3]。

1.3 正交试验

正交试验本文采用多组正交试验进行了基坑围护结构的稳定性和位移变形分析，即在给定因素水平的基础上，设计多组正交试验方案，计算每个方案下围护结构的变形和内力，进而确定最优方案。正交试验设计方法是一种在众多因素中找出最优水平组合的方法。

1.3.1 设计变量的选取

杭州某基坑支护结构的优化设计所涉及的因素很多，如果要一次性将所有的因素考虑到优化设计中，难度无疑是巨大的[4]。因此，本文暂时不去考虑某些因素对其产生的影响，而仅对其进行最优选择，对其进行支护结构细部设计，所确定的四个因素为：

桩径D（m），取值范围为：0.5m～1.1m；

桩长Hw（m），取值范围为：18.5m～24.5m；

支撑中心到地面的距离h（m），取值范围为：0.5m～2.5m；

支撑的截面面积A（m2），取值范围为：0.05～0.25m2。

1.3.2 正交试验设计

由于各个参数对基坑围护变形及成本的影响不同，故需对各个参数进行敏感性分析，以便针对这些因素进行针对性的分析和设计。采用正交设计法，对各个参数进行了敏感性分析。考虑到正交实验中有四个因素，所以使用L16（45）正交表来进行正交试验。在正交试验中，每个设计变量的变化水平为4个，桩径D（m）取0.7、0.8、0.9、1.0；桩长Hw（m）取18.5、20.0、21.5、23.0；支撑中心到地面的距离h（m），取0.5、1.0、1.5、2.0；支撑的截面面积A（m2），取0.05、0.10、0.15、0.20。

使用L16(45)正交表，对上述4个设计变量展开正交试验，利用二维PLAXIS有限元软件对表2中的每一种组合方案进行数值模拟，来计算出每一组试验的围护桩的侧向变形以及隧道的水平、竖向位移。

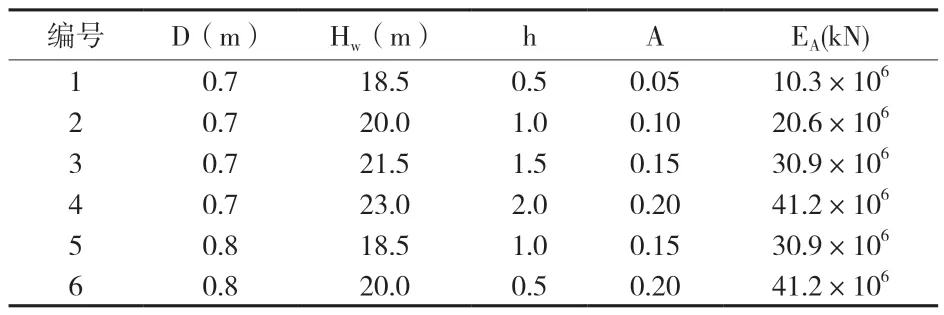
表2 支护结构细部参数正交试验取值表

1.4 模糊综合评价

在基坑的正交试验分析中，评价指标之间经常会互相矛盾，尤其是造价方面的评价指标和变形的指标之间。这个时候，必须引入一个评判指标，可以同时兼顾相互矛盾指标间的要求。所以，本文给出一种模糊综合评价的方法。这种方法可以有效地评估多个因素对结果的影响，从而更好地理解结果的准确性。此外，这种方法还可以应用于其他领域，以提高工作效率。第i次试验的j因素的隶属度dij定义如下式。

式中：

—第i次正交试验中yj评价因素的值；

在涉及多个目标的问题中，各个指标在整体效应中并不是一样的重要，有的指标相对较重要，有的则较次要一点，所以要确定各个指标的相对重要性。通常，对其相对重要性是由一组规范化的权来给定的，即在m个指标的情况下，一组，且0≤wi≤1，。对于权重的取值，与决策者的偏好也有关系，也可以根据工程经验和专家经验确定权重的取值，如果更具理论性的权重取值，也可以采用层次分析法计算各指标权重。因此，本文根据工程具体要求，以专家经验和以往案例确定各指标权重。

2 结果分析

本文的钢支撑的弹性模量为206×106kPa。通过PLAXIS有限元法，按照表2对各组进行正交试验参数的取值，得到的结果如图1所示。

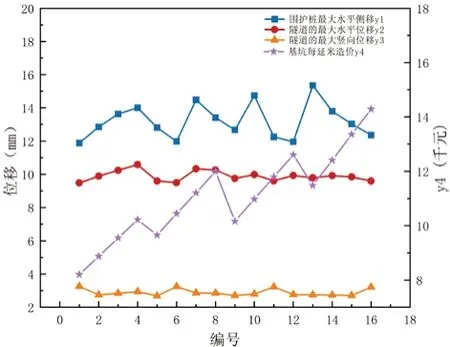
图1 正交试验组的计算结果

本文拟将围护桩最大水平侧移y1、隧道的最大水平位移y2、隧道的最大竖向位移y3以及基坑每延米的造价y4这4个因素作为优化的评判指标，这是一个多指标的问题。首先，通过对每一个指标的极差值进行逐项的极差值分析，找出影响各指标的主要参数。

2.1 各项指标极差分析

首先对围护桩最大水平侧移y1进行极差分析，并对其进行计算，得出结果如表3所示。表中的数据是在各个水平下对各个参数进行正交试验之和。从该表格可以看出，对围护桩水平侧移y1产生影响的主要参数为围护桩的直径D和支撑中心到地面的距离h。由于围护桩水平侧移y1愈小基坑愈安全。所以围护桩的直径应取D（3）=0.9m，支撑中心到地面的距离h（1）=0.5m。

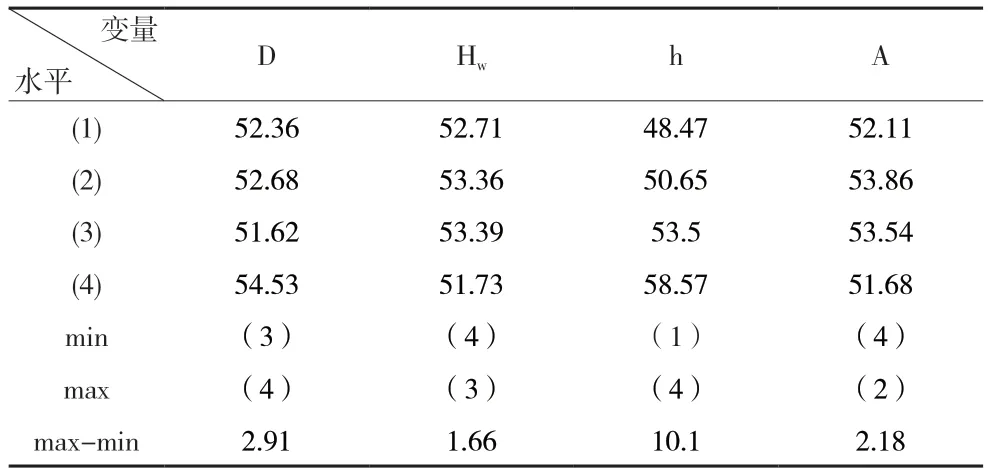
表3 围护桩最大水平侧移y1的极差分析 单位：mm

同理，对隧道的最大水平位移y2的做同样的分析，可知影响隧道最大侧移y2的主要参数是围护桩的桩长Hw和支撑中心到地面的距离h。因隧道水平位移y2越小越好，故围护桩的桩长Hw

（1）=18.5m，支撑中心到地面的距离h（1）=0.5m。

隧道的最大竖向位移y3的极差分析，由计算结果可知，对隧道竖向位移y3有影响主要参数为支撑中心到地面的距离h。因隧道竖向位移y3越小越好，故支撑中心到地面的距离h（2）=1.0m。

同理，对基坑每延米的造价y4进行差分析，可以知道，围护桩直径D和围护桩的桩长Hw是影响基坑每延的造价y4的主要参数。因基坑每延米造价y4越小越好，所以围护桩直径应取为D（1）=0.7m，围护桩的桩长Hw

（1）=18.5m。

对于围护桩的直径D，从减小围护桩侧向变形y1、隧道的最大水平位移y2和隧道的最大竖向位移y3的角度考虑，参数D应取为D（3）=0.9m；而从减小基坑每延米造价y4的角度考虑，参数D又取为D（1）=0.7m，故参数D的取值产生了矛盾。

2.2 多指标模糊分析

对于本文基坑支护的多指标问题，围护墙、隧道的变形与基坑的造价之间是矛盾的，所以寻找一种方案，有可能以低成本达到高要求是非常重要的。

2.2.1 综合评价参数建立

以围护墙最大水平侧移y1、隧道的最大水平位移y2、隧道的最大竖向位移y3以及基坑每延米的造价y4为评价因素，。因为正交试验次数为16次，所以评价集。

评价因素中，围护墙的侧移y1、隧道的最大水平位移y2、隧道的最大竖向位移y3和基坑每延米的造价y4均为偏小型指标，即越小越好。所以，可以根据式（1），对各个评价因素的隶属度值进行计算，由隶属度值构成模糊关系矩阵。本文根据专家经验和以往案例确定各指标权重。因此，确定4个指标的权向量为：

2.2.2 隶属度计算及分析

①模糊综合评价隶属度计算

根据模糊数学，模糊综合评价隶属度按式（1）计算，并计算得到各正交试验的模糊综合评价隶属度F，考虑到F为16×1的矩阵，以表4的形式表示。F中的值表示16组支护结构细部参数组合的模糊综合评价隶属度，亦可作为综合评价分数。从表中可知，第1组试验的模糊综合评价隶属度最大，f1=0.878，是这16组正交试验中的最优方案。为了找出16组正交试验外的可能最优方案，还需对模糊综合评价隶属度F做极差分析。

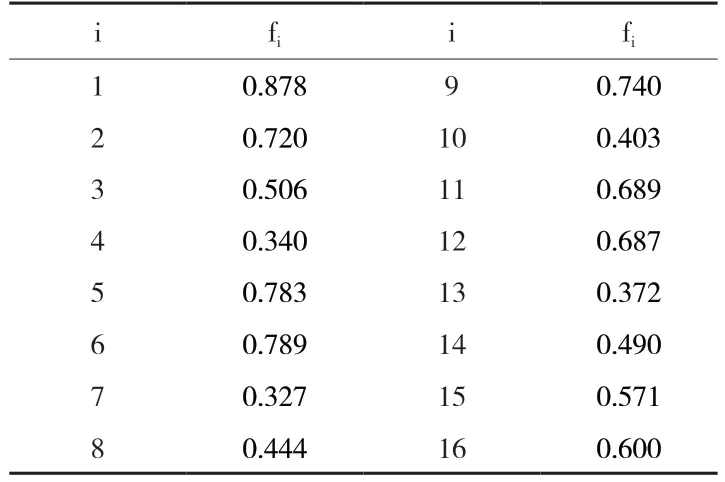
表4 模糊综合评价隶属度fi

②根据表4的模糊综合评价隶属度F，计算各因素不同水平对应的隶属度之和，找出各因素的最大模糊综合评价隶属度之和对应的水平，见表5。

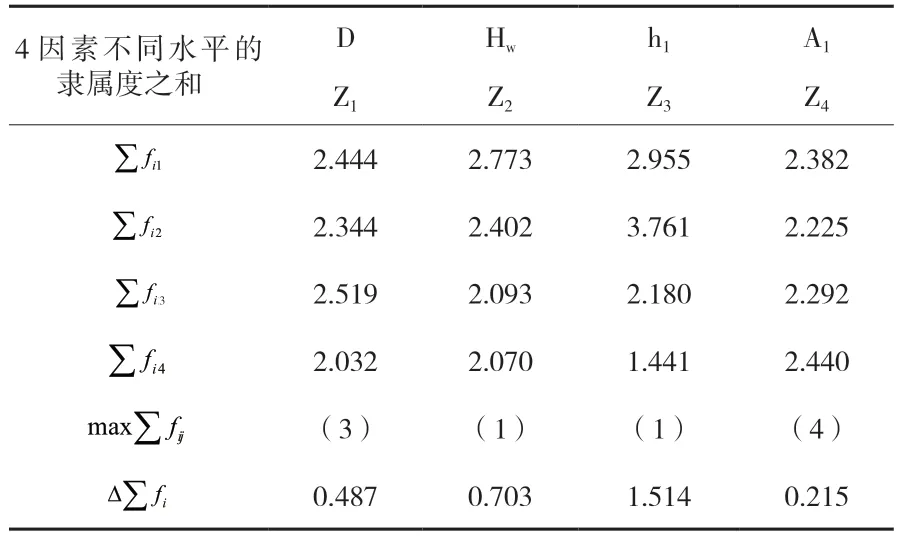
表5 模糊综合评价隶属度分析

为叙述方便，支护结构细部参数依次以Z1、Z2、Z3、Z4代称。表5中的为Zi因素在j水平下的模糊综合评价隶属度之和，max为Zi因素不同水平的模糊综合评价隶属度之和的最大值所对应的水平序号，Δ∑fi为Zi因素不同水平的模糊综合评价隶属度之和的极差，计算如式3。

3 结论

本文对杭州某基坑工程的优化设计实践，采用正交试验设计方法，以围护墙最大水平位移、隧道的最大水平位移和竖向位移以及基坑每延米的造价作为评价指标，根据专家意见确定各评价指标的权重，计算各正交试验的模糊综合评价隶属度，并进行极差分析获得结果如下：

（1）确定了四个支护结构的细部参数，选择了L16(45)正交表进行计算，在各个因素的取值范围中，分散地选取了4个水平，使用PLAXIS对各次试验的变形和基坑每延米造价进行计算，从而得出各次试验的评价指标。

（2）对有限元模拟结果进行各指标极差分析，发现随着围护墙、隧道的变形的增加，基坑的造价也随之增加。

（3）采用模糊数学的方法来解决在正交试验分析中遇到的指标矛盾问题，将各组合的模糊综合评价隶属度进行计算，给定各指标的权重，确定最佳的基坑支护结构细部参数：D=0.9m、Hw=18.5m、h=0.5m、A=0.2m2。