基于AGD-RRT算法的机械臂路径规划

周枫林，赵钒地，陈腾飞，龙厚云，王瑾元，李 光

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

随着人工智能技术的飞速发展，工业机器人已经被广泛地应用于汽车、船舶、航空等生产领域，面对日趋复杂多样的作业环境，传统人工示教编程的方式已经无法满足当前作业生产的需求，因此，如何利用智能算法使机器人能够快速、自主规划一条可行的运动轨迹，灵活高效地进行作业，成为当前工业机器人的一个研究热点。

工业机器人传统的路径规划方法有基于搜索和基于采样两类。A*算法[1]是基于搜索路径规划方法的常用算法之一，其搜索能力较强，但是不适合用于高维环境下的路径规划；RRT（rapidly-exploring random tree）算法[2]是基于采样的常用算法，其搜索能力较强，且无需将搜索空间栅格化，适用于不同维度环境下的路径规划。但是RRT算法存在采样随机、搜索时间较长、冗余节点较多、路径质量较差等问题。

鉴于RRT算法在路径规划过程中存在的问题，许多学者对此展开了大量的研究，并提出了各种改进策略[3-4]。如顾子侣等[5]提出了一种启发式扩展改进策略，因该策略在选择邻近节点时考虑了随机点到目标点的距离，故在一定程度上提高了算法的收敛速度，但是其并没有解决算法对复杂环境的适应性差的问题；刘紫燕等[6]提出了一种目标偏向策略，其随机树在拓展时以一定的概率向目标点方向拓展，因而该策略提高了算法的目标导向性，缩短了算法的搜索时间，但是概率阈值调试工作量较大；朱冰等[7]采用重选父节点与剪枝策略规划智能汽车路径，随机树在扩展时根据路径代价给新节点重新选择父节点，并且剪断原先的连接，使路径在搜索过程中达到渐进最优，但是这也增加了算法的搜索时间；辛鹏等[8]引入人工势场法，根据当前位置的目标引力以及障碍物斥力的合力方向来决定随机树的生长方向，这一方法虽然提高了算法的收敛速度，但是对复杂环境的探索能力不足；钟华庚等[9]通过约束随机树枝条的转角，重选父节点剔除冗余路段，该方法虽然提高了路径的质量，但是没能解决算法收敛速度慢等问题；张振等[10]通过约束采样方式，引入稀疏节点产生机制和动态采样域策略，避免了算法对已探索区域的重复探索，从而减少了无用节点的产生，但是该算法缺乏导向性，搜索时间较长。王坤等[11]提出了一种RRTconnect 算法，该算法在起点和终点处各生成一棵随机树，两棵随机树同时拓展直至相遇。该算法减少了算法的搜索时间，但是没能解决算法适应能力低和路径质量差等问题。

针对以上改进的不足，本文提出一种AGD-RRT算法，该算法采用启发式采样，引入了人工虚拟势场思想[12]，以提高算法的目标导向性，减少算法的搜索时间。且在搜索结束后，对轨迹进行平滑处理，以提高路径质量。

2 机械臂建模与碰撞检测

2.1 机械臂运动学模型

本文以图1a所示四自由度串联机械臂为研究对象，其结构模型如图1b所示，相关参数如表1所示。

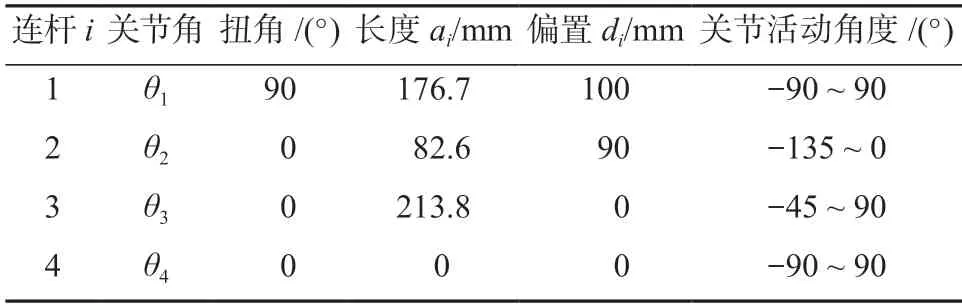
表1 机械臂D-H 参数Table 1 D-H parameters of the robotic arm

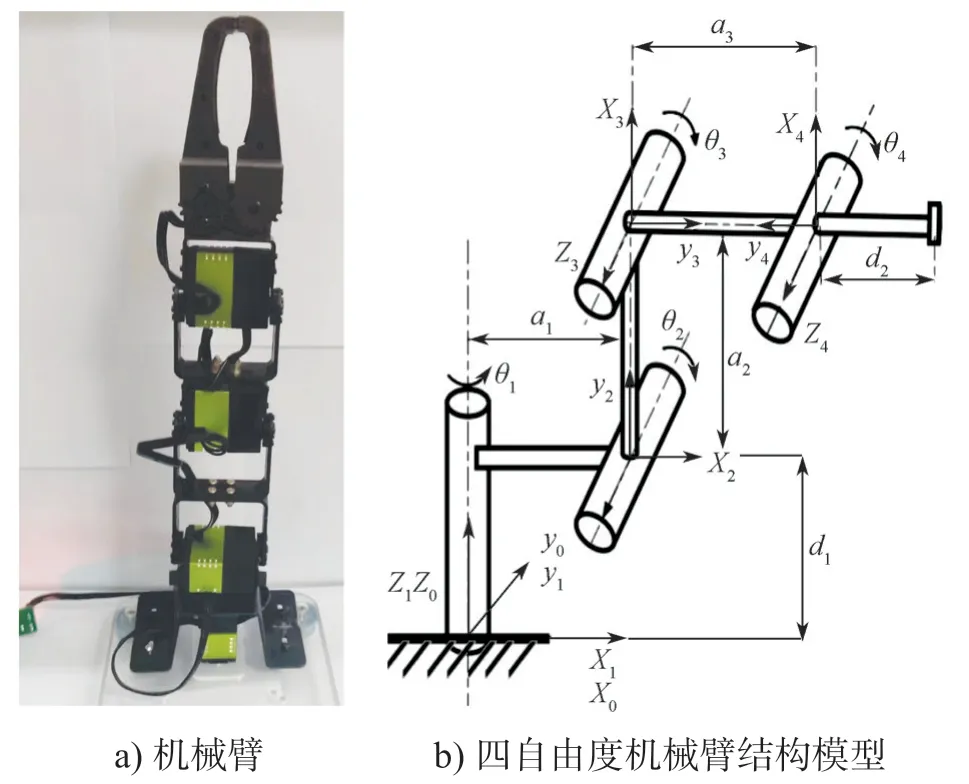
图1 机械臂运动模型与样机Fig.1 Robotic arm motion model and prototype

根据表1所示参数及机器人相邻两连杆间的齐次变换公式[13]，得到如下机械臂末端执行装置坐标系相对于基坐标系的齐次变换矩阵：

式（1）中：n、o、a3 个列向量和px、py、pz分别表示机械臂末端执行器坐标系在世界坐标系中的位置和姿态。

2.2 机械臂碰撞检测

碰撞检测是机械臂进行路径规划的重要环节之一，选取一个合适的碰撞检测方法可以有效提高机械臂路径规划效率。机械臂的碰撞检测包括如下两个部分：一个部分是机械臂与空间障碍物间的碰撞检测，另一个部分是机械臂工作时自身连杆的碰撞检测。为了能够快速准确地检测出机械臂的碰撞结果，本研究采用包围盒法[14]简化碰撞检测过程，将障碍物、机械臂关节分别用球体包围简化，机械臂连杆用圆柱体包围简化，简化后机械臂与障碍物的碰撞检测就变成了包络体中心线与球心的距离判断，如图2a所示，若球心到中心线的空间距离d1小于包围球半径与圆柱体包围盒半径之和，则机械臂连杆与障碍物有碰撞，否则没有碰撞。而机械臂自身连杆的碰撞检测则只需要检测非相邻两连杆中心线的空间距离d2，如图2b所示，比较d2与圆柱体包围盒的尺寸即可判断是否有碰撞。

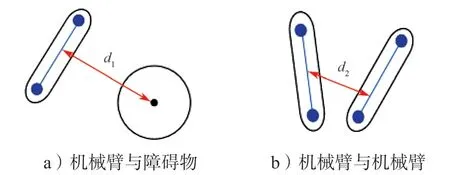
图2 机械臂碰撞检测原理示意图Fig.2 Schematic diagram of collision detection principle of the manipulators

3 AGD-RRT算法

3.1 RRT算法基本原理

RRT算法的概率完备、拓展能力较强，常被用于高维空间和复杂约束下的路径规划中。RRT算法的基本原理如下：将起始点xstart加入随机树tree，作为随机树tree的母节点，再在地图空间M中生成一个随机点xrand，然后遍历随机树tree，找到与随机点最近的节点xnearest；从节点xnearest开始往随机点方向以固定步长step生成一个点xnew，检测点xnew与节点xnearest之间是否存在障碍物，如果存在障碍物，则重新生成随机点xrand，若检测两节点间不存在障碍物，则将点xnew加入随机树tree中。重复以上步骤，直至随机树中存在某个子节点到目标点xgoal的距离小于所设置的权值r。

随机树的随机拓展，保证了算法的探索能力，最终总能搜索到一条可行的路径，但存在搜索效率低、导向性差、路径不平滑等问题。RRT算法的详细流程如图3所示。

图3 RRT算法流程图Fig.3 RRT algorithm flow chart

3.2 自适应目标导向

标准RRT算法的采样方式为全局均匀采样，该方式虽然保证了算法的探索能力，但是缺乏目标导向性，算法拓展随机，收敛速度较慢。刘奥博等[15]采用目标偏向策略提高RRT算法的导向性，该策略虽然让采样有了一定的偏向性，但是概率阈值依靠人工设置，需要进行反复调试，且不同地图所对应的最优概率阈值也不同，同时也不能根据随机树拓展边界的位置实时调整概率阈值。针对这一问题，本研究拟引入人工势场法生成自适应概率阈值。依据模拟人工势场法的虚拟势场思想，引入目标引力函数和目标方向的障碍物斥力函数。在斥力场中，仅考虑目标方向的最近障碍物对当前位置的影响，并且不限制斥力场范围。

引力场函数为

改进的斥力场函数为

引力为

改进的斥力为

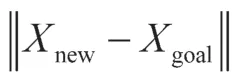
在随机树拓展过程中，若引力大于斥力，则说明可以继续向目标点方向进行拓展，此时的概率阈值增大，采样的目标趋向性增强，而随机性减弱；若斥力大于引力，则说明不宜继续向目标点方向且进行拓展，此时的概率阈值减小，采样的随机性增强，而趋向性减弱。由此可以得到如式（6）所示的概率阈值函数表达式。

为了防止概率阈值较大而目标点方向又无法拓展导致随机树局部锁死现象的产生，此处引入一种重置机制，即当遇到在目标点方向拓展失败的情况时，将概率阈值P0重置为0，随机树随机拓展，逃离锁死位置。

在得到概率阈值P0后，以概率P0向目标点方向采样，即以概率(1-P0)在地图范围内随机采样，随机树的采样方式如下：

式中P为一个0～1 的随机数。

3.3 贪婪收敛策略

标准RRT算法的收敛条件是，当最新添加的节点xnew与目标点xgoal之间的距离小于所设置的权值时，判定已经找到了目标点xgoal，路径规划完成。RRT算法概率完备，总能找到一条可行的路径，但是权值设置是否合理对算法有着重要影响：当权值设置过小时，算法的收敛速度会显著变慢；而当权值设置过大时，由于判断算法是否收敛时没有进行碰撞检测，难以保证规划路径的有效性，且当目标点处于空旷区域，随机树中已经生成了与目标点之间没有障碍物的节点时，随机树仍然以固定步长进行随机搜索扩展，因而严重减缓了算法的收敛速度。考虑到标准RRT算法收敛条件存在的不足，本文对算法的收敛条件进行了改进。贪婪收敛策略的详细步骤如流程图4所示。

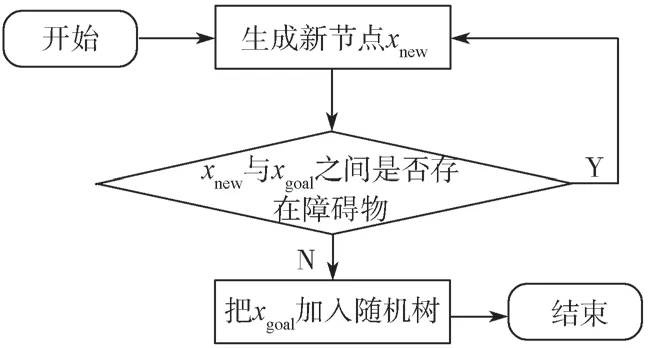
图4 贪婪收敛策略流程Fig.4 Greedy convergence strategy flow chart

本文对算法收敛条件的改进主要是在随机树每添加一个新的节点xnew后，对新节点xnew与目标点xgoal之间进行碰撞检测，如果有碰撞，则继续进行随机拓展，若检测没有碰撞，则将目标点加入随机树，路径规划完成。

3.4 路径优化处理

标准RRT算法规划出的路径冗余节点多、路线弯折、路径代价大，最终形成的路径质量较差。本文采用节点剔除的方式去除冗余节点，其原理如图5所示，从初始点n(1)开始，由近及远逐个对节点与起始点进行障碍检测，若点n(1)与点n(i)之间无障碍物（i为整数），点n(1)与点n(i+1)之间无障碍物，则连接起点n(1)与点n(i)，将点n(i)当作新的起始点，重复上述步骤，直至连接到终点。

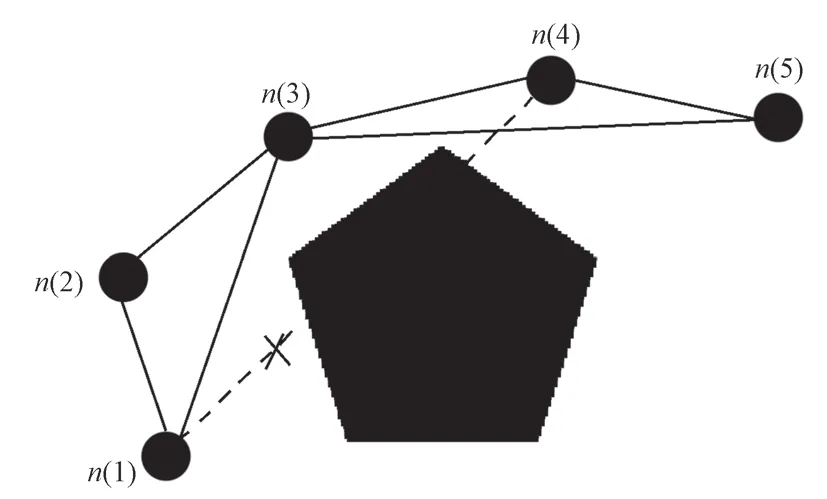
图5 冗余节点剔除原理示意图Fig.5 Redundant node removal principle diagram

经过剔除冗余节点处理后的路径存在较多的拐点，拐点的存在会影响机械臂运动的稳定性和精度，因此需要把简化后的路径在拐点处进行平滑处理。本文采用三次B 样条曲线对简化后的路径进行平滑处理，三次B 样条曲线函数如下：

式中：bi,3为三次B 样条曲线的基函数；ci为曲线的控制点，i=0,1,2,3。

3.5 AGD-RRT算法

结合以上方法得到一种AGD-RRT算法，算法流程如图6所示。

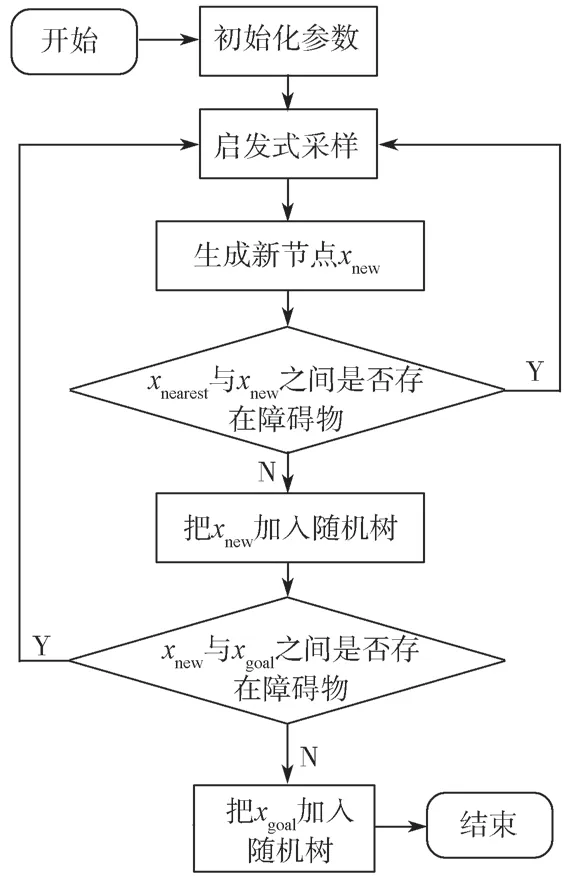
图6 AGD-RRT算法流程Fig.6 AGD-RRT algorithm flow chart

4 算法仿真与分析

为了验证所提算法的有效性和优越性，设计了两组对比试验，分别在二维空间和三维空间中进行对比仿真验证。在进行三维仿真实验时，将机械臂看作一个质点，不考虑机械臂自身连杆的碰撞以及机械臂与空间障碍物的碰撞。

实验方案如下：首先在matlab 软件中建立仿真地图，根据起始点与目标点的坐标，在图中绘出其位置，然后分别使用5 种算法进行避障路径规划。各算法分别进行50 次仿真实验，取其平均值作为最终结果。

4.1 二维空间仿真实验与分析

仿真实验所得5 种算法在二维空间的路径规划结果如图7所示。

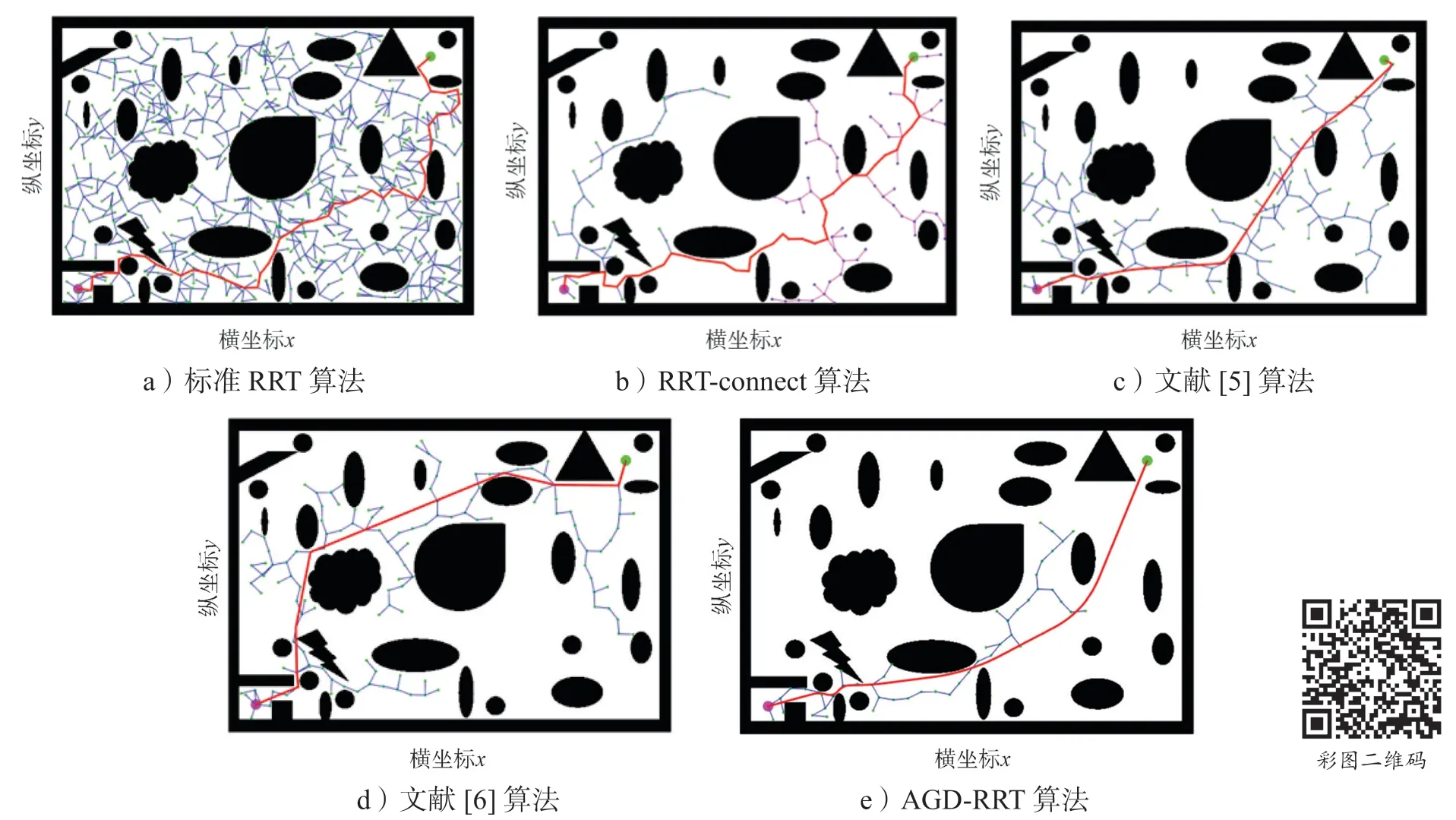
图7 5 种算法在二维空间的路径规划结果Fig.7 Path planning results of five algorithms in 2D space

如图7所示，仿真地图大小为624 mm×438 mm，紫红色圆点和绿色圆点分别代表起点和目标点，其坐标分别为(40，400)、(560，60)，引力系数λ1和斥力系数λ2分别取0.1,10 000，为了保证标准RRT算法和GB-RRT算法能够顺利通过地图中的狭窄位置，完成路径规划，经过多次实验，确定固定步长step取20 较为适合，仿真实验所用计算机配置为64位Windows 10 操作系统以及AMD Ryzen 5 2600X 处理器。

图7所示5 种算法进行路径规划的结果图中，蓝色和紫色线段为算法搜索过的路径，红色实线为最终路径。对比图7 中的5 个图可知，本文所提算法生成的无效节点最少，路径更光滑。表2 为二维空间中5 种算法的路径规划实验结果。由表2 可知，在二维空间的路径规划对比实验中，相较于RRT算法、RRT-connect 算法、文献[5]算法和文献[6]算法，AGD-RRT算法在搜索时间上分别减少了80.1%,29.6%,51.3%,45.7%，路径长度分别减少了25.1%,23.7%,1.7%,17.8%。AGD-RRT算法的结果均优于其他4 种算法，这是由于采用了自适应的目标导向策略，引导随机树向目标方向快速拓展，而贪婪收敛策略防止了随机树在目标周围时的盲目扩张。

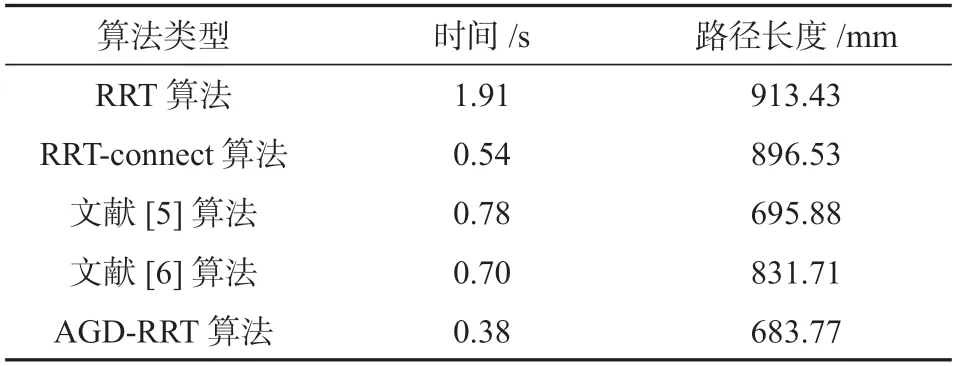
表2 二维空间中5 种算法的实验结果Table 2 Experimental results of five algorithms in 2D space

4.2 三维空间仿真实验与分析

如图8所示5 种算法进行路径规划的结果图中，地图尺寸为550 mm×550 mm×550 mm，球状物体为障碍物，绿色圆点和蓝色圆点分别代表起点和终点，其坐标分别为(50，50，50)、( 500，500，500)，固定步长step取30，其余参数与之前保持一致。图8 中红色实线为算法规划出的最终路径，根据对比可知，AGD-RRT算法的无效拓展相对较少，路径较为平滑，质量较好。表3 为三维空间中5 种算法的路径规划实验结果。

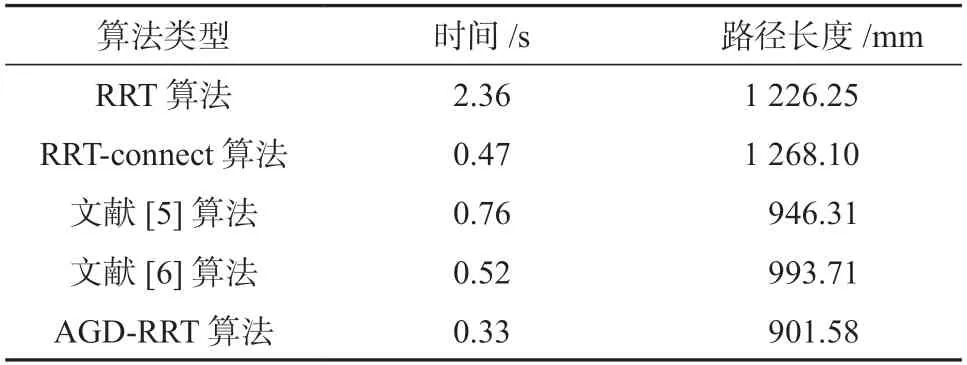
表3 三维空间中5 种算法的实验结果Table 3 Experimental results of five algorithms in 3D space

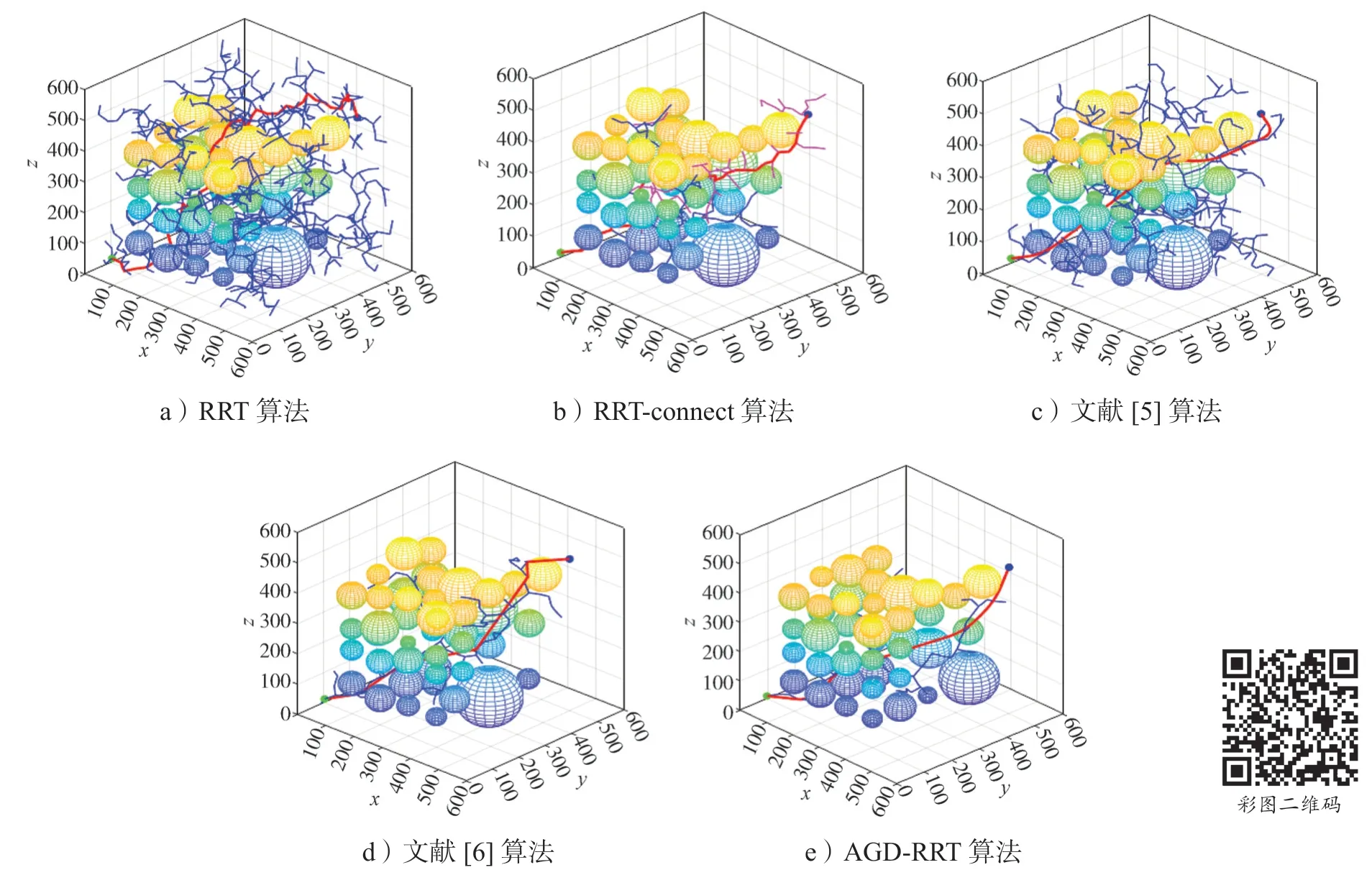
图8 5 种算法在三维空间的路径规划结果Fig.8 Path planning results of five algorithms in 3D space

由表3 可知，在三维空间的路径规划对比实验中，相较于RRT算法、RRT-connect 算法、文献[5]算法和文献[6]算法，AGD-RRT算法在搜索时间上分别减少了86.0%,29.8%,56.6%,36.5%，路径长度分别减少了26.5%,28.9%,4.7%,9.3%。从这个结果可以得知，本文所提出的改进RRT算法的性能相对于其它几种算法更优。

5 机械臂路径规划实验

机械臂的路径规划空间分为笛卡尔空间和关节空间。其中笛卡尔空间的路径规划需要对路径点求逆解，其逆解可能存在多组情况，机械臂碰撞检测与路径选取较为复杂。而关节空间的每个路径点映射到三维空间时，机械臂的位姿是确定的，其碰撞检测较为直观。因此，本文在机械臂的关节空间中进行路径规划。

考虑到机械臂的工作空间限制，仅在机械臂的前方设置了一个长方体形状的障碍物，让机械臂执行器的末端从起点运动到终点位置，起点和终点分别位于障碍物的两侧。起点和终点的坐标分别为（-45°,-60°,75°,5°）、(50°,-60°,80°,0°)，步长设置为15°，其余参数和以上实验一致。

为进一步验证所提路径规划方法在实际应用中有效性和可行性，通过实验验证，实验方案见图9。

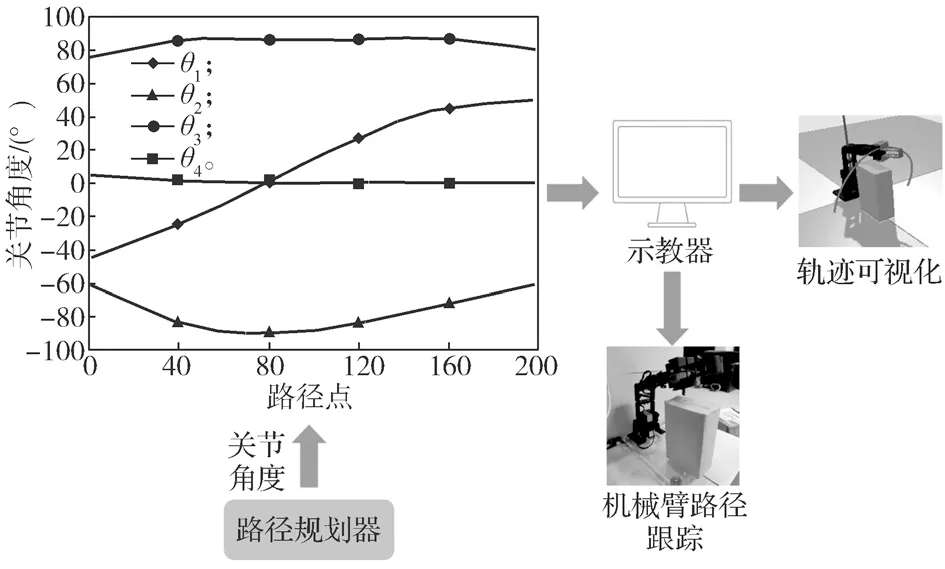
图9 机械臂路径规划实验方案Fig.9 Experimental scheme of robotic arm path planning

采用标准RRT算法和改进RRT算法为机械臂规划起始位姿到目标位姿的避障路径，将规划所得的路径数据导入机械臂示教器，机械臂对路径进行跟踪。图10所示为机械臂的一次避障路径规划过程。从图中可以看到机械臂能够准确避开障碍物，从起始点到达终点。重复上述实验10 次，两种算法均能准确地避开障碍物，但标准RRT算法的平均搜索耗时为17.74 s，平均路径长度为237.5°，而改进RRT算法的平均搜索耗时仅为4.27 s，平均路径长度为190.6°，这里的路径长度是指4 个关节角度变化量之和。从这一实验结果可知，改进RRT算法在耗时和路径长度方面比标准RRT算法更优，可见本文所提改进RRT算法对机械臂进行路径规划有效可行。

图10 机械臂避障过程图Fig.10 Robotic arm obstacle avoidance process

6 结语

针对机械臂路径规划，本文以标准RRT算法为基础，提出了一种AGD-RRT算法，解决了RRT算法搜索效率较低、适应性较差、路径质量较差的问题，算法改进如下：

1）提出一种动态的目标偏向概率函数，以实时调整对目标点进行采样的概率，达到自适应目标导向的效果，减少了无用节点的生成，提高了系统的收敛速度。

2）采用贪婪收敛策略，防止了随机树在目标周围时的盲目扩张。

3）使用了一种简单有效的节点拒绝方法与本文算法结合，避免了对重复区域的探索，提高了算法的收敛效率。

4）使用三次B 样条曲线对路径进行优化，使得机械臂各关节的运动平稳。

通过多组仿真实验对比，验证了AGD-RRT算法的有效性和可靠性。在机械臂的路径规划实验中，相较于标准RRT算法，AGD-RRT算法的平均搜索耗时减少了13.47 s，平均路径长度减少了46.9°。