改进烟花算法求解同时送取货选址路径问题

卞俊丽 张惠珍 刘冬 杨健豪

文章编号：1002-3100（2024）03-0006-06

摘  要：针对同时送取货的选址路径问题（Location-routing Problem with Simultaneous Pickup and Delivery，LRPSPD），设计一种改进烟花算法（Improved Firework Algorithm，IFWA）求解。首先，考虑仓库建设、车辆启用、车辆路径等成本因素，建立最小成本的LRPSPD模型，该模型强调需求点的送货需求和取货需求只能由一辆车同时进行服务。其次，设计一种改进烟花算法，该算法结合贪心聚类算法生成初始解，由烟花爆炸算子操作生成邻域解，利用变异操作协助产生新种群。最后，通过使用混合免疫算法、模拟退火算法求解相同算例，对结果进行分析比较，验证模型的可行性和改进算法的有效性。

关键词：选址路径；同时送取货；改进烟花算法；贪心聚类；变异操作

中图分类号：F253    文献标志码：A    DOI：10.13714/j.cnki.1002-3100.2024.03.002

Abstract： This paper studied the location-routing problem with simultaneous pickup and delivery（LRPSPD）and designed an improved fireworks algorithm（IFWA）to solve the problem. Firstly， a LRPSPD model of minimizing warehouse construction cost， vehicle using cost and vehicle routing cost was build. The model emphasized customers' delivery and pickup needs should be served by one same vehicle. Secondly， an improved firework algorithm（IFWA）was designed to solve the model. The IFWA generated initial solutions via combining greedy clustering algorithm， produced neighborhood solutions by firework explosion operator operations， and created new populations through mutation operations. Finally， a mixed immune algorithm and simulated annealing algorithm were used to solve the same cases respectively， and the results are verified the feasibility of the model and effectiveness of the IFWA.

Key words： location-routing problem; simultaneous pickup and delivery; firework algorithm; greedy clustering; mutation operation

0  引  言

選址决策与路径决策是物流供应链中两个相互依赖的关键问题，对公司的运营有着重要的影响。选址-路径问题（Location-routing problem， LRP）一直是当前物流供应链以及运筹学优化的研究热点。众多学者将LRP问题与实际情况结合起来，提出拓展的LRP问题，比如有容量选址路径问题（Capacitated LRP， CLRP）^[1]、低碳选址路径问题（Low-Carbon LRP， LCLRP）^[2]、同时送取货选址路径问题（LRP with Simultaneous Pickup and Delivery， LRPSPD）^[3]等。

在现代物流中，对于存在多级加工厂和供应链的企业来说，同时送取货的物流配送模式更加贴合实际情况，因此，LRPSPD也逐渐成为国内外众多学者研究的热点课题。Khodashenas等^[4]提出了需求和成本参数不确定的两阶段LRPSPD问题，并使用NSGA-II和MOLAO算法对其进行求解。Dehghan等^[5]研究了在中断风险状态下的同时送取货问题，并设计三种元启发式算法进行求解，并研究其算法性能。Yilmaz等^[6]研究了可变邻域搜索算法求解电动车同时送取货问题。张颖钰等^[7]研究了带时间窗的多中心半开放式VRPSDP问题研究，并设计混沌变异头脑风暴算法来求解。李珺等^[8]提出基于模拟退火与自适应大规模邻域搜索相结合的混合优化算法研究同时送取货车辆路径问题。陈其赛和倪静^[9]提出了同时送取货电动车选址路径问题并用混合模拟退火-蚁群优化算法求解该问题。

针对LRPSPD问题，大部分学者都是将需求点的送货需求和取货需求分开计算，并派出相应的送货和派送车辆来满足需求点的不同需求，存在如下问题：（1）资源浪费，如车辆送货回程时空车，取车时空车，造成空车装载资源闲置等；（2）路径不合理，如需要两辆车分别服务需求点的取货需求和送货需求，且两辆车的行驶路径重复。以上问题极大地增加了物流成本。本文通过改进传统的LRPSPD模型，将送货和取货需求同时考虑进车辆负载中，并根据车辆负载的动态变化选择合适的需求点进行分配，防止因车辆容量问题导致需求点服务损失。此外，提出一种求解LRPSPD问题的烟花算法，采用爆炸算子对烟花进行操作，生成一定数量的火花，利用变异操作随机对火花进行操作，在增加种群多样性的同时探索更好的解决方案。本文对算法的参数设置上采取Taguchi试验设计方法确定参数组合，并通过AM分离法改进Pordhon标准数据库获取算例。最后将本文算法，模拟退火算法和混合免疫算法对算例分别求解，验证所提算法的有效性。

1  同时送取货选址路径问题（LRPSPD）

1.1  LRPSPD问题描述与模型假设

本文研究的LRPSPD模型可以描述如下：在物流网络中存在多个仓库候选点和需求点，且需求点同时具有送取货需求，车辆从其所属仓库出发，为其分配的需求点一次性提供先送货，再取货的服务。该模型需要确定仓位的选址，车辆数量和车辆对其分配需求点的服务路线。

本文基于如下假设构建模型：（1）每个需求点只能接受一个仓库和一辆车服务，且其服务容量须满足需求点的需求量；（2）任意两个仓库之间相互独立，没有车辆来往；（3）所有车辆提供服务后须返回其出发仓库；（4）所有车辆为同一类型。

1.2  模型构建

以往文献大多是分别计算取货和送货需求，并派出相应的取货和送货车辆来满足需求量的不同，这样操作不仅复杂，而且还易造成资源浪费和行驶路径重复，极大地增加了物流成本。因此，本文统一计算需求量的送货与取货，并将其与车辆的实时负载能力联系起来，共同构成车辆的负载约束。这样，该路线的车輛同时进行提货和送货业务，满足每个需求点的两种需求，并根据车辆的负载分配合适的需求点，确保满足每一个需求点的需求，从而避免了车辆的空载发生和运输路线的复制。

1.2.1  模型参数说明

模型中所使用的参数变量定义如下：

1.2.2  模型建立

目标函数（1）表示总成本最小化，其中第一部分是仓库的选址成本，第二部分是车辆的启动成本，第三部分是运输路径成本；约束条件（2）和（3）表示被选中的仓库服务容量不得小于需求点的送取货需求量；约束条件（4）和（5）表示车辆的服务容量不得小于需求点的送取货需求；约束条件（6）和（7）表示节点的负载能力；约束条件（8）和（9）表示每个需求点只有一辆车和一个仓库可以为其提供服务；约束条件（10）表示每辆车最多只能被使用一次；约束条件（11）表示任意两个仓库之间相互独立，没有车辆来往；约束条件（12）表示节点的流量平衡；约束条件（13）表示消除子回路；约束条件（14）表示只有当需求点被分配到仓库时，才能接受服务；约束条件（15）～（18）表示变量之间的关系；约束条件（19）表示决策变量的取值范围。

2  求解LRPSPD的改进烟花算法

烟花算法是由Tan等^[10]在2010年提出的一种优化算法。该算法将一定范围的爆炸区域视作搜索空间，每个烟花都代表一个可行解，根据烟花的适应度值进行迭代。适应度高的烟花质量好，爆炸半径小，生成的火花数量多，局部搜索能力强；适应度低的烟花质量相对差一些，其爆炸半径大，具有更好的全局搜索能力^[11]。烟花算法计算原理简便，且全局寻优能力较强^[12]。因此，本文设计一种改进的烟花算法来求解LRPSPD问题。

针对LRPSPD模型的具体特点，本文将烟花算法与贪心聚类算法和邻域搜索相结合，设计了一种改进的的烟花算法。首先，在初始解的生成部分参考贪心聚类思想，提高初始解的质量。其次，使用烟花算法生成火花，使用变异操作变异部分烟花。最后，使用选择策略来选择较好的个体迭代为新的烟花。

本文设计的烟花算法主要由四个部分组成：（1）初始化：采用贪婪策略对需求点进行聚类和划分，然后根据每个集群的中心分配仓库和车辆，并形成派送路径；（2）爆炸算子：根据爆炸强度和爆炸幅度将烟花引爆，产生火花。本文利用变异操作生成新的火花个体，扩大可行解的范围。所采用的变异操作主要包括：交换、插入、逆转和单点变异；（3）选择策略：选择优秀的火花个体作为新的烟花进行迭代，不断优化烟花种群；（4）接受机制：以一定的概率接受一个好的解，从而跳出局部最优。

算法中涉及到的解的编码、初始解的生成和变异操作介绍如下：

2.1  解的编码

同时送取货选址路径问题可以形成长度为2n的解，解的构成主要分成两部分。1，…，n部分代表需求点和仓库点的分配关系，n+1，…，2n部分代表需求点的被服务次序，假设有4个候选仓库点，10个需求点，则解的长度为20，图1给出了一个可行解。

由图1中1，…，n部分可知，4个仓库中4号仓库未开放，10个需求点被分配到剩下3个仓库中，需求点与仓库的所属关系如下（需求点编号→仓库编号）：1，3，8，10→3；4，7，9→2；2，5，6→1；由n+1，…，2n部分可知每个仓库服务需求点的顺序，例如3号仓库服务的需求点为1，3，8，10。1号需求点的被服务次序为第10个，3号需求点为第6个，8号需求点为第1个10号需求点为第9个，因此，3号仓库所服务的需求点的次序为8→3→10→1。

2.2  初始解的生成

对于初始解的生成，本文受贪心聚类的启发，采用需求点分块、仓库指派和扫描路径三段式生成策略，具体如下：

（1）根据车辆的容量、需求点的送取货需求和需求点间的距离，将需求点分块。第一步，随机选择需求点ka。第二步，在车辆容量的约束下选择距离最近的需求点kb，并从需求点索引中删除需求点ka和kb。第三步，从剩下需求点中选择离kb最近的需求点kc，并判断车辆的容量约束是否被超出。如果不被超出，则将kc加入当前区块，否则，该需求点不被该车辆考虑。直到所有需求点都被分块，记录需求点的分块计数。

（2）每个细分的需求点群体被拉入一个超等需求点。具体操作方法是用公式（20）计算每个需求点分块的重心，用该重心作为超等需求点的坐标，然后用公式（21）计算每个仓库到每个超等需求点的距离之和，在满足仓库容量的前提下分配超等需求点，确定需求点和仓库的所有权。

（3）对每个仓库所服务的需求点通过扫描法形成派送路线。扫描法是指用极坐标表示仓库及其指定需求点的位置，然后以任意一点为起点，设置其角度为零度，以车辆容量为限，顺时针方向扫描需求点，形成一个序列的需求点，直到扫描完所有需求点，并生成仓库的配送路线方案。

2.3  变异操作

设计的变异操作主要包括交换、插入、反转和单点变异。通过变异操作生成爆炸火花和变异火花，可以在增加种群多样性的同时探索更好的解决方案。

2.3.1  交  换

随机选择一个解的1，…，n部分，从中随机选择两个位置，交换其序列号。例如：图2中2号和10号是选中的位置，通过交换他们所属的仓库，可以生成一个新的解决方案。

2.3.2  插  入

随机选择一个解的1，…，n部分，随机选择两个位置，将第二个位置的序号插入到第一个位置上，依次更替序号。例如：图3中选择10号需求点，插入到2号需求点的位置，插入点为2号需求点。10号需求点的所属仓库从3号变成了2号，2～9号需求点的所属仓库也相应变化。

2.3.3  逆  转

随机选择一个解的1，…，n部分，从中随机选择两个位置，将这两个位置的序号倒序插入。例如：图4中选择2号和10号这两个需求点，将它们和它们之间的需求点倒序插入。

2.3.4  單点变异

随机选择一个解的1，…，n部分，从中随机选择一个位置，随机生成新的仓库为其提供服务。例如：图5中红色标注的是2号需求点，变异之后，2号需求点便由2号仓库对其进行服务。

2.4  算法步骤

改进的烟花算法解决同时送取货问题的步骤如下：

Step1：确定算法的各种控制参数，包括初始种群数Nq、迭代次数D、爆炸火花数Mp和烟花爆炸半径参数R等；

Step2：结合贪心聚类策略生成初始种群Nq，计算每个烟花的适应度值，记录当前最优解；

Step3：开始迭代，根据相关控制参数，利用适应度值计算烟花的爆炸火花数和爆炸半径；

Step4：对烟花种群进行变异操作（交换，插入，逆转，单点变异），生成爆炸火花，将生成的爆炸火花中不满足条件的火花映射回可行空间，更新个体；

Step5：对于由爆炸火花和当前烟花组成的新候选种群，根据选择策略选择新的种群；

Step6：判断当前迭代次数是否满足最大迭代次数，如果满足，执行Step7，否则，返回Step3；

Step7：满足终止条件，停止算法并输出结果。

3  算例对比与结果分析

为了验证改进烟花算法求解LRPSPD模型的有效性，仿照文献^[13]中的测试数据，生成8-2（8个需求点，2个候选仓库）和15-5（15个需求点，5个候选仓库）两组数据，并采用AM分离法^[14]生成需求点送取货需求，相关数据见表1。

3.1  算例参数设置

设置IFWA的相关参数，利用IFWA针对CLRP的Prodhon算例求解，设定种群数目M为50。其他影响着算法性能的重要参数有烟花数Nq、爆炸火花数Mp、最大半径参数R、突变火花数Mq和迭代次数D等。利用Taguchi试验的设计方法（Design of Experiment，DOE）^[15]对此类参数进行灵敏度分析。构建正交试验表L16对50-5-1算例求解，给出每个参数的4个合理水平值。将每个参数独立运行20次，参数的水平、正交表和AVG统计以及参数响应值数据如表2至表4所示。

由表4可以看出，爆炸火花数Mp的范围最大，说明爆炸算子在解集中的运算对算法性能的影响最大。迭代次数D对1.5n（n为需求点数）次后算法的收敛性影响不大。此时种群趋于最优解，群体中个体值接近一致，算法呈现收敛状态。当参数Mq为2n时，更有利于算法的收敛。综合考虑，推荐的参数值为Nq=2n，Mp=2n，R=0.5n，Mq=2n，D=1.5n。

3.2  算例结果与分析

实验所用硬件环境为Intel（R）Core（TM）i5-8250U CPU@1.60GHz，8GB内存，64位Windows10操作系统，使用MatlabR2020a进行编程。实验得到两组算例的求解结果如表5所示。

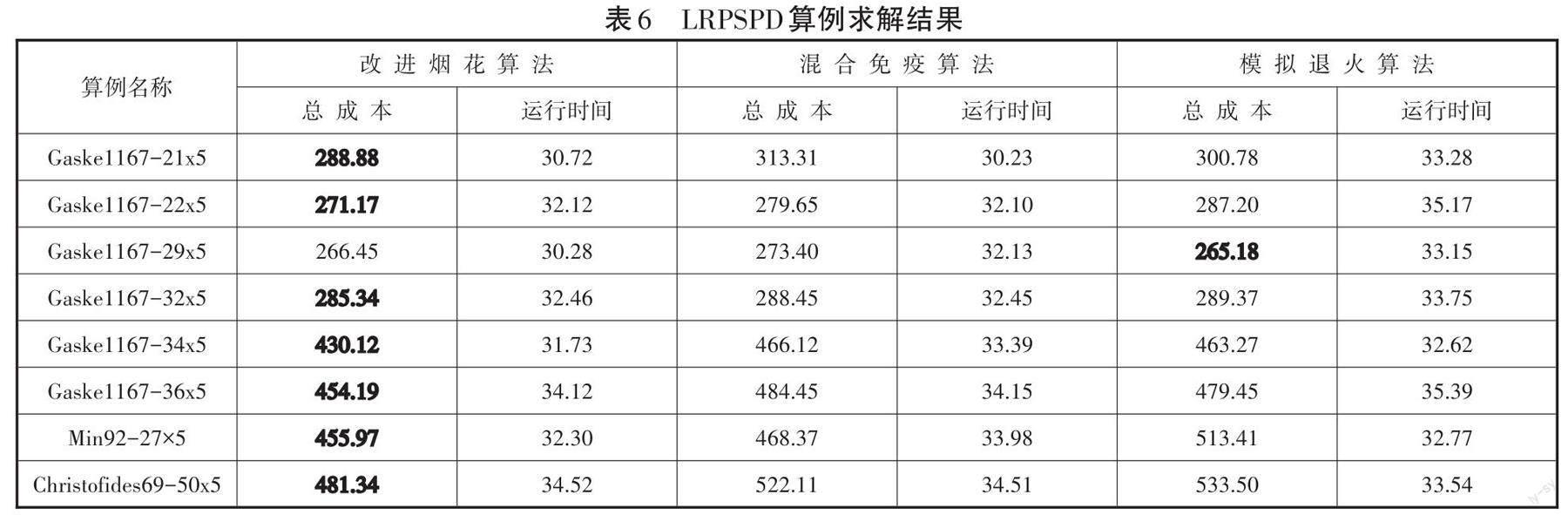
由表5可知，改进的烟花算法可以在较短的时间内获得相对于精确算法的较好解。总体而言，CPLEX的结果不仅验证了模型的准确性，而且证实了算法的有效性。为了更好地验证算法的求解效率，文章对CLRP标准算例库中的Prodhon算例进行改进以适应模型的求解，并采用本文算法（IFWA）、混合免疫算法^[16]和模拟退火算法^[17]等3种算法求解。每个例子求解20次，记录最优解和运行时间，求解结果如表6所示。

由表6可知，改进烟花算法和混合免疫算法结果对比，虽然混合免疫算法在运行时间上稍优，但是总成本均劣于利用改进烟花算法求解的结果。改进烟花算法和模拟退火算法结果对比，在运行时间方面，改进烟花算法全面占优；在总成本方面，除了Gaskell67-29x5外，其余7个算例利用改进烟花算法求解结果均明显优于模拟退火算法。

4  结  论

本文研究同时送取货选址路径问题，一方面，在需求点有同时取货和送货需求的情况下，根据需求点分布，合理选择仓库设施；另一方面，根据车辆容量和最大行驶距离调度车辆，有效规划行驶路线，减少资源浪费，降低配送成本。文章将烟花算法与贪心聚类和邻域搜索相结合，设计了一种求解LRPSPD的改进烟花算法，并与模拟退火算法和混合免疫优化算法对比，结果表明该算法在运行时间和解的质量上均有明显提升。文章所构建模型和设计算法可为相关决策者对物流网络的优化提供有效参考。

参考文献：

[1]  AKPUNAR ？魻 S， AKPINAR S. A hybrid adaptive large neighbourhood search algorithm for the capacitated location routing problem[J]. Expert Systems with Applications， 2021，168：114304.

[2] 张坤，张惠珍，马良，等. 分布估计灰狼算法求解低碳选址路径问题[J/OL]. 系统管理学报：1-16[2023-03-22]. https：//kns-cnki-net.webvpn.usst.edu.cn/kcms/detail/31.1977.n.20221021.1055.002.html.

[3]  WANG X. Research on hybrid immune algorithm for solving the location-routing problem with simultaneous pickup and delivery[J]. Journal of Cases on Information Technology （JCIT）， 2022，24（5）：1-17.

[4]  KHODASHENAS M， KAZEMIPOOR H， NAJAFI S E， et al. A two-stage uncertain model to arrange and locate vehicle routing with simultaneous pickup and delivery[J]. International Journal of Research in Industrial Engineering， 2022，11（3）：273-305.

[5]  DEHGHAN M， HEJAZI S R， KARIMI-MAMAGHAN M， et al. Capacitated location routing problem with simultaneous pickup and delivery under the risk of disruption[J]. RAIRO-Operations Research， 2021，55（3）：1371-1399.

[6]  YILMAZ Y， KALAYCI C B. Variable neighborhood search algorithms to solve the electric vehicle routing problem with simultaneous pickup and delivery[J]. Mathematics， 2022，10（17）：3108.

[7] 张颖钰，吴立云，贾胜钛. 带时间窗的多中心半开放式VRPSDP问题研究[J/OL]. 系统仿真学报：1-12[2023-03-27]. https：//doi.org/10.16182/j.issn1004731x.joss.22-0727.

[8] 李珺，段钰蓉，郝丽艳，等. 混合优化算法求解同时送取货车辆路径问题[J]. 计算机科学与探索，2022，16（7）：1623-1632.

[9] 陈其赛，倪静. 基于同时送取货电动车选址路径问题优化研究[J]. 上海理工大学学报，2021，43（5）：515-522.

[10]  TAN Y， ZHU Y. Fireworks algorithm for optimization[C] // International Conference in Swarm Intelligence， 2010：355-364.

[11] 马创涛，邵景峰. 烟花算法改进BP神经网络预测模型及其应用[J]. 控制工程，2020，27（8）：1324-1331.

[12] 聶浩程. 生鲜农产品冷链物流配送网络优化研究[D]. 杭州：浙江理工大学，2022.

[13]  YU V F， LIN S Y. Solving the location-routing problem with simultaneous pickup and delivery by simulated annealing[J]. International Journal of Production Research， 2016，54（2）：526-549.

[14] 刘冬，张惠珍，刘亚平，等. 改进蘑菇算法与开放式送取货选址路径问题[J/OL]. 控制工程：1-12[2023-03-27]. https：//doi.org/10.14107/j.cnki.kzgc.20210630.

[15]  ZHANG B， PAN Q， GAO L， et al. An effective modified migrating birds optimization for hybrid flowshop scheduling problem with lot streaming[J]. Applied Soft Computing， 2017，52：14-27.

[16]  QIAO J， LI F， YANG S， et al. An adaptive hybrid evolutionary immune multi-objective algorithm based on uniform distribution selection[J]. Information Sciences， 2020，512：446-470.

[17]  VINCENT F Y， LIN S Y. A simulated annealing heuristic for the open location-routing problem[J]. Computers & Operations Research， 2015，62：184-196.

收稿日期：2023-03-28

基金项目：国家自然科学基金项目（72101149）；教育部人文社会科学基金项目（21YJC630087）

作者简介：卞俊丽（1989—），女，江苏盐城人，上海理工大学管理学院硕士研究生，研究方向：智能优化；张惠珍（1979—），女，山西忻州人，上海理工大学管理学院，副教授，硕士生导师，研究方向：运筹学、智能优化；刘  冬（1996—），男，河北保定人，上海理工大学管理学院硕士研究生，研究方向：智能优化。

引文格式：卞俊丽，张惠珍，刘冬，等. 改进烟花算法求解同时送取货选址路径问题[J]. 物流科技，2024，47（3）：6-11.