气溶胶粒径吸湿增长因子的机器学习模型
米家媛,李 娜,佟景哲,倪长健* (.成都信息工程大学大气科学学院,四川 成都 605;.辽宁省气象装备保障中心,辽宁 沈阳 066)
大气气溶胶是指悬浮在地球大气中的液态或固态粒子[1].气溶胶吸湿能增强颗粒物表面的非均相反应速率,显著改变气溶胶的化学组分、结构和形态特征,进而对天气气候、大气环境以及人体健康产生重要影响[2-4].大气气溶胶吸湿性是联系气溶胶微物理和化学参数的纽带,在整个大气气溶胶科学研究中处于基础地位[5].
气溶胶粒径吸湿增长因子定义为气溶胶粒子在吸湿后与吸湿前的粒径之比,是表征气溶胶吸湿性的通用参数.目前,学者们主要通过场外观测并结合反演算法对气溶胶粒径吸湿增长因子进行测量.Yan等[6]通过外场观测得到北京城区和上甸子的气溶胶吸湿增长因子分别为(1.26±0.15)和(1.24±0.11);庄雯雯等[7]的观测结果表明,上海地区霾期间气溶胶吸湿增长因子在春季、冬季、夏季和秋季分别为1.56、1.39、1.37、1.29;张智察等[8]基于Mie 散射理论反演了成都地区气溶胶粒径吸湿增长因子,其值为(1.26±0.25).上述研究指出,气溶胶粒径吸湿增长因子随时空存在较大的差异.早在 1969年,Kasten[9]就基于气溶胶与水汽平衡增长理论提出了气溶胶粒径吸湿增长的通用模型;孙景群[10]针对不同气溶胶类型进一步提出了修正的气溶胶粒径吸湿增长模型;张智察等[8,11]通过分析成都地区气溶胶粒径吸湿增长因子的变化特征,构建了本地化的气溶胶粒径吸湿增长模型,并提出气溶胶粒径吸湿增长因子和气溶胶散射吸湿增长因子的函数关系.由上述分析可见,气溶胶粒径吸湿增长因子随时空存在较为显著的变化,相对湿度是其中的关键影响因子.
研究表明[12-13],黑碳的老化可导致黑碳气溶胶在形貌、粒径、混合态以及化学组成上的显著变化,进而增强气溶胶的吸湿性.张城语等[14]以相对湿度(RH)与黑碳质量浓度(CBC)为自变量构建了气溶胶散射吸湿增长因子的双变量模型,显著提升了成都地区气溶胶散射吸湿增长因子的模拟精度.另外,考虑到黑碳以及不同粒径气溶胶质量浓度变化对气溶胶等效复折射率的影响[15],佟景哲等[16]重新构建了气溶胶散射吸湿增长因子的解释变量集,提出了气溶胶散射吸湿增长因子的多变量GAM 模型,进一步提升了高湿条件下气溶胶散射吸湿增长因子的模拟效果.Chen等[17]指出,气溶胶粒径谱是气溶胶散射吸湿增长因子变化的主控因子.为此,米家媛等[18]以RH、CBC、CPM1/CPM2.5、CPM2.5/CPM10和CBC/CPM1(CPM1、CPM2.5、CPM10分别为PM1、PM2.5、PM10的质量浓度)为自变量构建了气溶胶粒径吸湿增长的GAM 模型,并验证了该模型的适用性.上述研究成果不仅揭示了气溶胶散射吸湿增长和气溶胶粒径吸湿增长多因素影响的复杂性和不确定性,也集中指明了CBC变化对气溶胶粒径吸湿增长的重要作 用.
机器学习算法可以把大量非线性特征量拟合在一起,相较于 GAM 模型,具有鲁棒性.目前,LightGBM、CatBoost 和XGBoost 模型是机器学习的三大主流算法,已被广泛应用于医学、交通运输及环境气象等领域的研究[19-21].本文基于Mie 散射理论和免疫进化算法反演气溶胶粒径吸湿增长因子,构建了气溶胶粒径吸湿增长的机器学习模型,分析了不同解释变量对机器学习模型模拟效果的影响,降低了气溶胶粒径吸湿增长模型在高湿条件下的模拟偏差,旨在从方法论的角度为气溶胶粒径吸湿增长因子的科学表征提供新途径.
1 资料及方法
1.1 资料及资料处理
利用成都市2017 年10~12 月浊度计、黑碳仪和GRIMM180 环境颗粒物分析仪的逐时观测数据,结合该时段同时次大气能见度(V)、相对湿度(RH)和二氧化氮(NO2)监测资料,基于Mie 散射理论和免疫进化算法反演气溶胶粒径吸湿增长因子(Gf),获得样本合计1221 个.
大气能见度(V)由SWS-200 能见度仪进行监测,相对湿度(RH)由WS600 一体式气象站进行监测,等效黑碳质量浓度(CBC)由AE-31 型黑碳检测仪获取,PM1, PM2.5和PM10的颗粒物质量浓度(CPM1,CPM2.5和CPM10)由GRIMM180 环境颗粒物监测仪实时测量,NO2质量浓度由Thermo42i 化学发光NO、NO2-NOx分析仪进行监测.
监测点位于成都市环境保护科学研究院综合大楼楼顶(30°39'N,104°02'E),距离地面高度21m,四周2km 内无高大建筑物,视野开阔;另外,观测点周围为集中居住区,5km 范围内无明显工业大气污染源.数据的质量控制参见文献[8,11,14,16].
1.2 气溶胶粒径吸湿增长因子的反演
基于Mie 散射理论,并借鉴“干”气溶胶等效复折射率参数化方案的研究成果,文献[8]构建了下述目标函数,见式(1).
式中:r(RH)为环境条件下的气溶胶粒子半径;n[r(RH)]为环境条件下气溶胶的粒子谱分布;a(RH)为环境条件下气溶胶粒子的尺度参数;m(RH)为气溶胶等效复折射率;Qap[a(RH),m(RH)]和Qsp[a(RH),m(RH)]分别为环境条件下气溶胶散射效率因子和吸收效率因子;bext(RH)为波长为550nm的大气消光系数;bap、bsg和bag分别为波长为550nm 的环境条件下气溶胶吸收系数、大气气体的散射系数和吸收系数.利用免疫进化算法求解该目标函数,据此反演气溶胶粒径吸湿增长因子(Gf),并验证了求解结果的精度.反演流程及反演结果分析详见文献[8].
1.3 气溶胶粒径吸湿增长因子的机器学习算法
机器学习算法主要包括线性回归算法、决策树算法和梯度增强算法等,本文选取了梯度增强算法中的三种主流算法(LightGBM、CatBoost 和XGBoost)构建气溶胶粒径吸湿增长模型.其中,LightGBM 基于Histogram 决策树、单边梯度采样和互斥特征捆绑优化使其较传统梯度增强算法具有更好的准确性、更快的训练速度以及大规模处理数据能力;CatBoost 参数少、准确性高,同时支持类别型变量,能高效合理地处理类别型特征,并改善模型的梯度偏差及预测偏移问题,提高了传统梯度增强算法的准确性和泛化能力;XGBoost 模型是用多个弱分类器组合成一个强分类器,在传统梯度增强算法基础上引入了一个新技术,对损失函数做二阶泰勒展开,并在目标函数之外使用正则化技术(通过在损失函数中添加一个新项来实现的),避免过拟合现象的产生,整体求最优解,使得模型在调整期间训练速度更快、鲁棒性更强[22-24].
本文通过调用Python 中的XGBRegressor、CatBoostRegressor、LGBMRegressor 库来构建XGBoost、CatBoost 和LightGBM 模型,通过多参数共同作用防止模型在估算过程中出现过拟合现象,从而提高模型估算的准确性;并随机抽取70%样本作为训练集,30%样本作为测试集,由此获得训练样本855 个,测试样本366 个;采用十折交叉法进行模型的验证,以实测值和预测值的决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)为标准对结果进行评估.通过对上述模拟结果的对比分析,探讨XGBoost、CatBoost 和LightGBM 三种机器学习算法的适用性,为气溶胶粒径吸湿增长模型的改进提供方法论.
1.4 气溶胶粒径吸湿增长机器学习模型的构建
通过对以相对湿度为单变量的气溶胶粒径吸湿增长模型模拟偏差的分析,结合黑碳气溶胶老化过程中吸湿性改变以及气溶胶等效复折射率参数化方案的研究成果[15,25,26],文献[18]提出了气溶胶粒径吸湿增长因子多变量GAM 模型.本文参照文献[18]构建气溶胶粒径吸湿增长因子的解释变量集,包括RH、CBC、CBC/CPM1、CPM1/CPM2.5、CPM2.5/CPM10,上述参数的含义同前.
首先选取XGBoost、CatBoost、LightGBM 三种机器学习算法的基准模型,对应的默认值参数分别为: n_estimators=100, max_depth=3, learning_rate=0.1, min_child_weight=1, subsample=1, gamma=0, colsample_bytree=1, reg_alpha=0;iterations=1000,depth=6, learning_rate=0.03, 12_leaf_reg=3, bagging_temperature=1, border_count=128, random_strength=1;num_leaves=31, max_depth=-1, learning_rate=0.1,subsample=1, min_data_in_leaf=20, lambda=0.针对前述855 个训练样本构建气溶胶粒径吸湿增长模型,训练结果表明, XGBoost、CatBoost 和LightGBM 三种基准模型的决定系数(R2)分别为0.801、0.835 和0.838,均方根误差 (RMSE)分别为0.197、0.185 和0.182,平均绝对误差(MAE)分别为0.096、0.086 和0.085.
进一步使用超参数自动搜索模块GridSearch_CV 对 XGBoost、CatBoost 和LightGBM 算法进行调整,依次列举参数的可能取值,得到组合结果后生成“网格”,将各网格结果分别带入上述3 种机器学习算法进行训练,并利用交叉验证评估训练集中的数据,经过参数调优得到的最优参数组合如表1 所示.
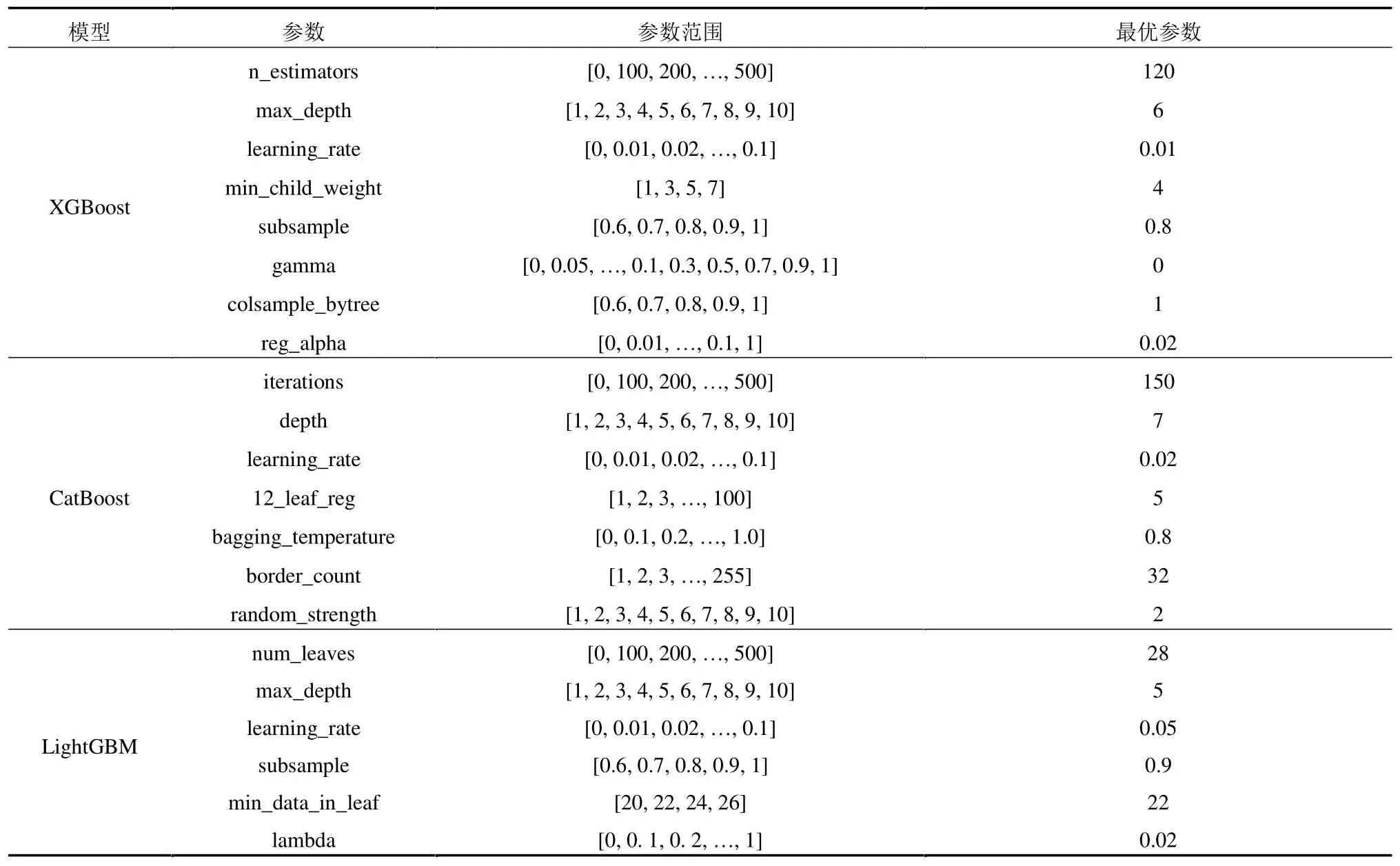
表1 三种机器学习模型的最优参数Table 1 Optimal parameters of three machine-learning models
同样针对前述855 个训练样本,基于最优参数组合构建气溶胶粒径吸湿增长模型,参数调优后3 种机器学习模型的性能如图1 所示.由图1可见,3 种机器学习算法经过参数调优后提高了机器学习算法的预测精度,其中,LightGBM 模型取得了最佳的模拟效果,CatBoost 和XGBoost 模型次之.


图1 参数调优后3 种机器学习模型性能可视化对比Fig.1 The visualization comparison chart of three machine learning models performance after parameters tuning
2 结果与讨论
2.1 气溶胶粒径吸湿增长机器学习模型的测试
针对366 个测试样本,分析了基于最优参数组合构建气溶胶粒径吸湿增长机器学习模型(XGBoost 模型、CatBoost 模型和LightGBM 模型)的适用性,并与气溶胶粒径吸湿增长因子多变量GAM 模型[18]的模拟结果进行了比对分析.如图2 所示,多变量GAM 模型、XGBoost 模型、CatBoost 模型和LightGBM 模型模拟值的决定系数(R2)分别为0.879、0.887、0.888 和0.898,残差平方和(RSS)分别为2.278、2.274、2.253 和2.069.上述结果表明,(1) 3 种气溶胶粒径吸湿增长机器学习模型的测试结果和图1 的相应模拟结果总体相当,即机器学习模型具有很好的稳定性和泛化能力;(2)就3 种气溶胶粒径吸湿增长机器学习模型而言,LightGBM 模型的测试结果最优,能最佳地表征气溶胶粒径吸湿增长因子与多变量的复杂非线性关系;(3) 3 种气溶胶粒径吸湿增长机器学习模型的测试结果相较于多变量GAM 模型均有显著提升,高湿(RH≥85%)是影响模型模拟误差的重要因素.机器学习通过拟合多维非线性特征量,将机器学习算法和模型相结合不断进行调整和优化,具有更强的非线性映射能力和鲁棒性以及优化计算能力.
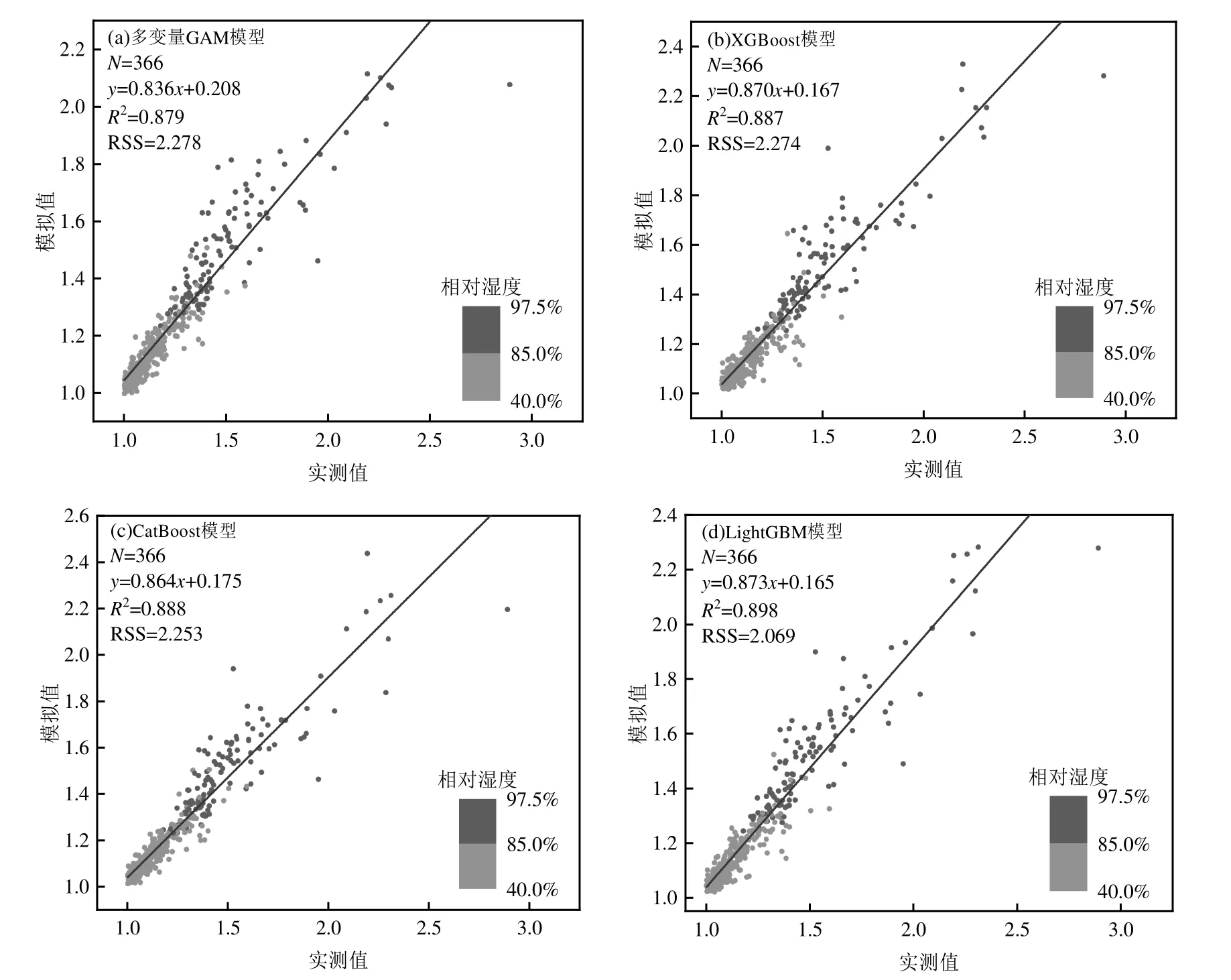
图2 4 种气溶胶吸湿增长模型的模拟结果Fig.2 Fitting results of four aerosol hygroscopic growth models
由于气溶胶中的硫酸盐、硝酸盐和铵盐等无机成分及部分有机物粒子具有吸湿性,在不同水汽条件下其微物理参数会发生变化,致使气溶胶粒子群理化及光学性质不断改变.刘凡等[27]针对成都地区的研究指出,随着相对湿度的增大,硫氧化率和氮氧化率显著增加,导致二次气溶胶在气溶胶中的占比进一步升高,气溶胶结构和化学组分更趋复杂.另外,受气溶胶二次非均相化学反应和黑碳气溶胶老化等因素的共同影响,气溶胶粒径吸湿增长因子对多因素响应的不确定性增强.已有研究表明[11,18],气溶胶粒径吸湿增长因子传统单变量统计模型在低湿(RH<85%)条件下的模拟值与实测值之间的平均绝对误差处于较低水平且波动较为平缓,但在高湿(RH≥85%)条件下的模拟值与实测值之间的平均绝对误差随相对湿度增加显著增大,这也对气溶胶粒径吸湿增长因子传统单变量统计模型的适用性提出了挑战.气溶胶粒径吸湿增长因子传统单变量统计模型如式(2)所示[10],其中,μ为常系数,RH0=40.
为进一步评估气溶胶粒径吸湿增长机器学习模型在高湿(RH≥85%)条件下的模拟效果,针对112个高湿样本,由图3 可见,气溶胶粒径吸湿增长传统单变量统计模型以及 XGBoost、CatBoost 和LightGBM 模型的R2分别为0.669、0.764、0.808 和0.811,RSS 分别为1.616、1.457、1.160 和1.156.这一测试结果表明,高湿气象条件下气溶胶理化过程的复杂性是气溶胶粒径吸湿增长因子模拟不确定性的重要来源,由此导致气溶胶粒径吸湿增长因子在高湿条件下模拟误差随相对湿度的增加而显著增大,基于机器学习的气溶胶粒径吸湿增长模型显著降低了气溶胶粒径吸湿增长传统单变量统计模型在高湿条件下的模拟偏差,其中, LightGBM 模型的模拟结果仍为最优.
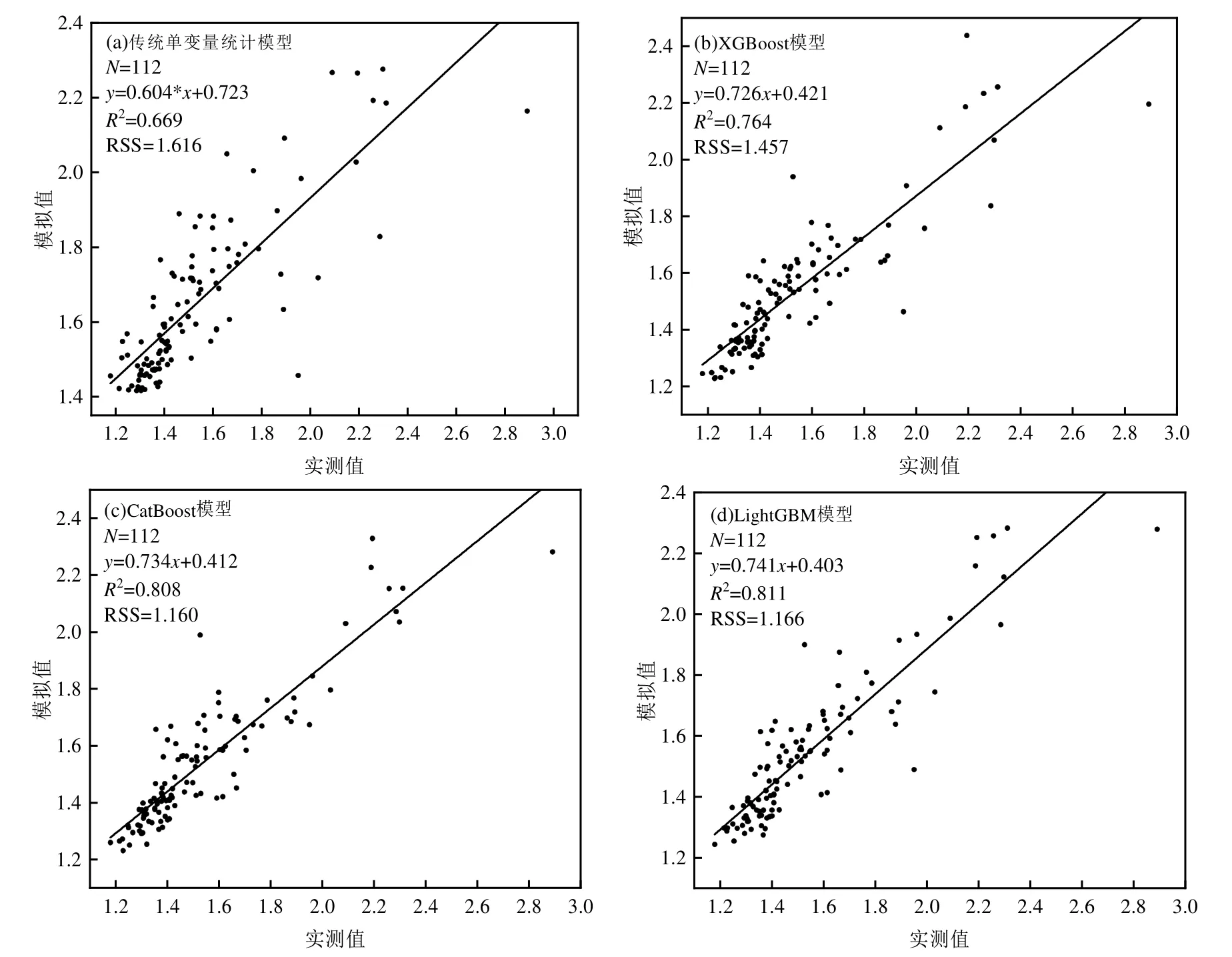
图3 高湿条件下气溶胶吸湿增长因子的模拟结果Fig.3 Fitting results of aerosol hygroscopic growth factor at RH>85%
2.2 多因素解释变量的重要性评价
通过比较以上3 种机器学习模型的 feature importance 属性,研究多因素解释变量集中的各个变量对模型模拟效果的影响程度,对比分析结果如图4所示,虽然3 种机器学习模型中的各个变量重要性排序不尽相同,但相对湿度(RH)和黑碳质量浓度(CBC)的变量重要性均排名前二,说明无论是采用哪种机器学习模型,RH 和CBC均是决定气溶胶吸湿增长模型模拟效果的关键性影响因素.研究表明[28-29],黑碳的老化过程是使其具备吸湿性的关键因素,不同老化程度的黑碳颗粒物吸湿增长也具有显著差异,从而引起气溶胶粒径吸湿增长因子的复杂变化;另外,由于气溶胶等效复折射率实部和虚部与CBC/CPM1、CPM1/CPM2.5和CPM2.5/CPM10呈现出一定的相关性[15,30],并且能够显著影响气溶胶粒径吸湿增长.即除RH 外,气溶胶结构和化学组分(CBC、CBC/CPM1、CPM1/CPM2.5和CPM2.5/CPM10)也是影响气溶胶粒径吸湿增长的重要因素,其中以CBC的影响尤为显著.上述结果表明:解释变量的完整性是气溶胶粒径吸湿增长模型模拟效果的重要影响因素,完整的解释变量结合更为复杂的统计模型有助于提升气溶胶粒径吸湿增长的模拟效果.

图4 使用3 种机器学习模型的特征重要性排序Fig.4 Ranking diagram of feature importance using three machine-learning models
测试表明,在解释变量集中分别去除排名前2的变量(RH 和CBC),3 种机器学习模型的R2均出现了显著下降,这也佐证了文献[14,18]的研究结果.
综上,机器学习模型具有更强的非线性映射能力以及优化计算能力,能更好地反映气溶胶粒径吸湿增长因子对多因素的复杂响应关系,这也为气溶胶粒径吸湿增长的科学表征提供了一条新途径.
3 结论
3.1 以RH、CBC、CBC/CPM1、CPM1/CPM2.5以及CPM2.5/CPM10为解释变量集,利用 3 种机器学习算法(XGBoost、CatBoost 和LightGBM)构建了气溶胶粒径吸湿增长模型,3 种模型的决定系数(R2)分别为0.887、0.888 和0.898,其中,LightGBM 模型取得了最佳的模拟效果,CatBoost 和XGBoost 模型次之.
3.2 高湿条件下,多变量GAM 模型及3 种机器学习模型的R2分别为0.758、0.764、0.808 和0.811,传统单变量统计模型及3 种机器学习模型的RSS 分别为1.616、1.457、1.160 和1.156.因此,气溶胶粒径吸湿增长机器学习模型显著降低了传统单变量统计模型在高湿(RH≥85%)条件下的模拟偏差,同时也提升了气溶胶粒径吸湿增长多变量GAM 模型的计算精度.
3.3 气溶胶粒径吸湿增长因子和气溶胶散射吸湿增长因子的演化成因具有同源性,除相对湿度之外,确认了黑碳是气溶胶吸湿增长模型的主控变量,这也为气溶胶粒径吸湿增长因子多变量模型的构建提供了新途径.

