基于模糊n-cell数的非线性投入产出模型解的存在性

陆星宇,叶国菊,刘尉

(河海大学理学院, 江苏 南京 210098)

0 引言

模糊数是模糊理论研究的重要内容,有关模糊数的概念最早由Zadeh等[1]研究提出的。2011年,Wang系统总结了模糊数理论,给出了相应的结果与应用[2]。模糊n-cell数是一类特殊的n维模糊数,可以用来表示不确定信息,在许多领域都有广泛的应用,如模糊识别、分类、排序等[3]。

不动点理论在过去的几十年里不断发展,其形式与内容呈现出多样化的特点,为后续研究提供了更广的空间。模糊不动点理论是在研究模糊数空间中的不动点定理时建立起来的,是传统不动点理论的一种推广。Wang等[4-5]研究了一类模糊增映射的不动点定理,解决了3类平衡模型解的存在性问题。 Lakshmikantham等[6]提出了混合单调算子的概念并给出了相应的不动点定理。Chang等[7]将混合单调算子与模糊数结合起来,得到了一维模糊数空间中的一类带紧性的混合单调不动点定理。有关单调算子的不动点理论在Banach空间中讨论得比较完善,但其在模糊数空间中的研究还不够全面。因此,受文献[6-7]中结论的启发,本文中给出了模糊n-cell数空间中的混合单调不动点定理,丰富了模糊n-cell数空间中的不动点理论,并为研究非线性投入产出模型解的存在性提供了理论基础。

不动点理论也是研究各类算子方程的重要工具,在经济均衡理论中发挥着巨大的作用,是处理平衡模型解的存在性的有力工具。投入产出模型是经济模型中的一个经典问题,Liu等[8],Zhao等[9]等利用不动点定理讨论了该模型解的存在性问题,得到了模型的数值解法。Mattila[10]将模糊线性系统和投入产出模型结合,用数值方法研究了该模型的解。近年来,投入产出模型也广泛应用于多目标优化问题上[11]。鉴于投入产出模型的变量具有不确定性,本研究建立了一种以模糊n-cell数为变量的非线性投入产出模型,并结合不动点定理得到了该模型解存在的一些结论。

1 预备知识

设(Rn,d)为完备度量空间,K(Rn)表示Rn的非空紧子集全体。对任意A,B∈K(Rn),集合A和B的Hausdorff度量表示为

定义1[1]设u是论域Rn到[0,1]上的一个映射,即

u:Rn→[0,1],x→u(x),

称u是Rn上的一个模糊集,u(x)称为模糊集u的隶属函数。对给定x∈Rn,u(x)称为x对u的隶属程度,Rn上的模糊集全体记为F(Rn)。

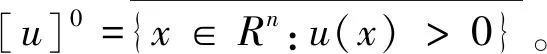
设u,v∈En,k∈R1,En中的加法、乘法和数乘分别表示为

其中,

定义2[3]设u∈En,若对任意的α∈[0,1],[u]α是一个n维方体,即

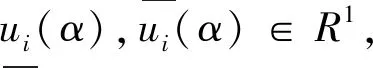
设ui∈E1,i=1,2,…,n,由ui构成的模糊数组称为n维模糊向量,记为(u1,u2,…,un)。n维模糊向量全体称为n维模糊向量空间,记为(E)n。

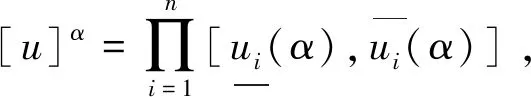
注2引理1表明模糊n-cell数与n维模糊向量可相互表示,即对于由模糊n-cell数u确定的n维模糊向量(u1,u2,…,un),表示法u=(u1,u2,…,un)存在且唯一。

设u,v∈L(En),记u=(u1,u2,…,un),v=(v1,v2,…,vn),对任意的k∈R1,L(En)中的加法、乘法与数乘分别表示为

u+v=(u1+v1,u2+v2,…,un+vn);

uv=(u1v1,u2v2,…,unvn);

ku=(ku1,ku2,…,kun).

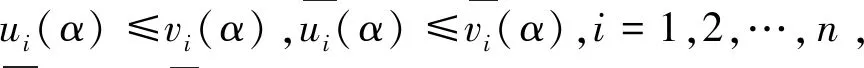
设u,v∈L(En),α∈[0,1],L(En)中的度量表示为

文献[2]中还给出了模糊n-cell数空间中的多种度量,并证明了在度量D下(L(En),D)为完备度量空间。

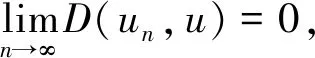
定义5[2］设非空集合U⊆L(En),若存在uU∈L(En),使得对任意的u∈U,有u≤uU,则称U关于序≤有上界,uU称为U的一个上界。若U有上界,且存在U的一个上界uS∈L(En),使得对U的任意上界uU,有uS≤uU,则称uS为U的上确界,记为uS=supU。 下界与下确界可类似定义。若U关于序≤既有上界又有下界,则称U是有界的。

引理2[2]设非空集合U⊆L(En),若U有上界,则存在上确界;若U有下界,则存在下确界。

定义6[6]设模糊映射A:L(En)×L(En)→L(En)。若对任意的(u1,v1),(u2,v2)∈L(En)×L(En),u1≤u2,v1≥v2,有A(u1,v1)≤A(u2,v2),则称A为混合单调的。

定义7[6]设模糊映射A:L(En)×L(En)→L(En)。若存在(u*,v*)∈L(En)×L(En),满足A(u*,v*)=u*,A(v*,u*)=v*,则称(u*,v*)为A的耦合不动点。若存在u*∈L(En),使得A(u*,u*)=u*,则称u*为A的不动点。

定义8[7]设模糊映射A:L(En)×L(En)→L(En)。若存在常数k∈(0,1),使得对任意的(u,v)∈L(En)×L(En),有D(A(u,v),A(v,u))≤kD(u,v),则称A为压缩映射。

2 混合单调映射不动点定理

设u0,v0∈L(En),u0≤v0,L(En)中的序区间记为[u0,v0]={u∈L(En):u0≤u≤v0}。

定理1证明记M={(u,v)∈[u0,v0]×[u0,v0]:u≤A(u,v),A(v,u)≤v}。由(u0,v0)∈M知M非空,不妨设

M1={u∈[u0,v0]:∃v∈[u0,v0]使(u,v)∈M,u≤A(u,v)},

M2={v∈[u0,v0]:∃u∈[u0,v0]使(u,v)∈M,A(v,u)≤v}。

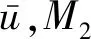
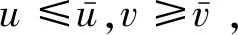
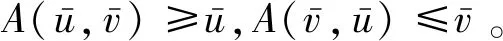
(1)

(2)

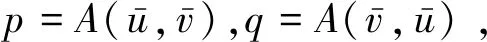
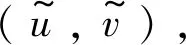
证毕。

对于模糊映射A:[u0,v0]×[u0,v0]→L(En)。若A将[u0,v0]×[u0,v0]中的任意有界集映为L(En)中的相对紧集,则称A是紧的。若A又是连续的,则称A为全连续的。

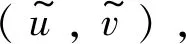
un=A(un-1,vn-1),n=1,2,3,…

(3)

vn=A(vn-1,un-1),n=1,2,3,…

(4)

确定的序列{un},{vn}满足

u0≤u1≤…≤un≤vn≤…≤v1≤v0

(5)

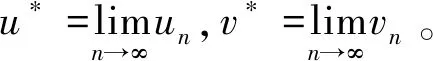
定理2的证明取n=1时将(3)、(4)式代入u0≤A(u0,v0),A(v0,u0)≤v0得u0≤u1,v1≤v0。注意到A为混合单调的,所以

u1=A(u0,v0)≤A(v0,u0)=v1,

故u0≤u1≤v1≤v0,利用归纳法假设

un-1≤un≤vn≤vn-1,

再由A为混合单调可得

un=A(un-1,vn-1)≤A(un,vn)=un+1,

vn=A(vn-1,un-1)≥A(vn,un)=vn+1,

un+1=A(un,vn)≤A(vn,un)=vn+1,

因此un≤un+1≤vn+1≤vn,假设成立,展开即(5)式成立。

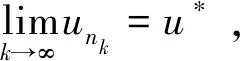
D(unk0,u*)<ε,

所以当n≥nk0时,由序列{un}的单调递增性有unk0≤un≤u*,故

D(un,u*)≤D(unk0,u*)<ε,

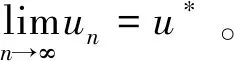
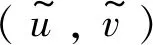
利用归纳法易证得

(6)

(7)

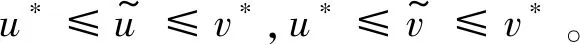
证毕。

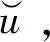
wn=A(wn-1,zn-1),n=1,2,3,…

(8)

zn=A(zn-1,wn-1),n=1,2,3,…

(9)

定理3的证明注意到A为压缩映射,由定义8知存在k∈(0,1),使得对任意的(u,v)∈[u0,v0]×[u0,v0],有D(A(u,v),A(v,u))≤kD(u,v),又A亦符合定理2的条件,故可将定理2中的式(3)、(4)代入该式得

D(un,vn)=D(A(un-1,vn-1),A(vn-1,un-1))≤kD(un-1,vn-1),

即

D(un,vn)≤knD(u0,v0)

(10)

对任意选取的初始点(w0,z0)∈[u0,v0]×[u0,v0],利用迭代格式(8)(9)易证得

un≤wn≤vn

(11)

un≤zn≤vn

(12)

证毕。

3 模糊非线性投入产出模型解的存在性

3.1 投入产出模型的早期研究概述

国民经济各个部门之间存在着相互依存和相互制约的关系,各部门在彼此影响下形成了一个共同体,每个部门在运转过程中对其他部门产品的消耗称为该部门的投入,而这些消耗的产品在经过该部门加工处理后得到的新产品称为产出。如何根据各部门之间投入与产出的平衡关系,确定各部门的产出水平以满足社会需求,即各部门的总投入与总产出达到平衡,是投入产出模型主要研究的问题,该模型简称IO模型,是由美国数学家W.Leontief等[12-13]首先提出并研究的,几十年来在理论和实践方面有了很大的发展。国内学者那日萨等[14]对静态非线性IO模型进行了深入的研究,取得了一定的成果。

早期的IO模型主要考虑线性模型。设有n个部门依次表示为1,2,…,n,在一定时期内,第i部门的总投入记为xi,总产出记为yi,初始投入记为ci,外部需求记为di,第i部门对第j部门的投入记为xij(也表示第j部门对第i部门的需求),i,j=1,2,…,n,于是可得出总产出与总投入的表达式为

(13)

(14)

由W.Leontief均衡理论知,应当保证每一部门的总投入等于总产出,即对第i部门而言,xi=yi,因此当i=j时,式(13)与式(14)是等价的。故本文中将在平衡条件xi=yi下考虑由(13)式确定的IO模型解的存在性问题。一般情况下,投入与产出都是动态变化的,在研究各部门投入与产出的平衡关系时,就需要一个稳定的指标来刻画它,于是引入直接消耗系数aij来表示第j部门的单位产出对第i部门的直接消耗,即

代入式(13)得

(15)

若记投入向量X=(x1,x2,…,xn)T,需求向量d=(d1,d2,…,dn)T,直接消耗系数矩阵A=(aij)n×n,则式(15)可表示为

X=AX+d

(16)

式(16)称为线性IO模型的代数方程,在线性模型下,我们总是假设每个部门只生产唯一的产品,不同部门生产的产品都是不同的并且aij是常数,由此可导出线性IO模型的基本问题:记I表示单位实矩阵,对于任意的需求向量d,是否存在投入向量X满足方程(I-A)X=d。虽然该模型可以清晰地表达出投入产出量的关系,并且可以通过代数方法来求解投入向量X,但在实际生活中,许多变量都呈现出非线性关系,此时原先的假设便不再满足,导致该模型无法对投入产出量做长期的预测,因此需要考虑更一般的模型。非线性模型是指原模型中第i部门对第j部门的投入xij非线性且唯一依赖于第j部门的总产出xj,记为xij=xij(xj),且记直接消耗系数aij=aij(xj),系数矩阵A=A(X),故非线性IO模型表示为

X=A(X)X+d

(17)

对于(17)式中的直接消耗系数矩阵A(X),早期的一些研究都是在假设A(X)为单调矩阵下考虑的,但在实际情况下,这不是一个普遍现象,因为随着科技水平的进步,A(X)会表现出某一部分元素单调递增而另一部分单调递减的情况,因此在分析非线性IO模型时要考虑到这种情况。同时,大部分非线性IO模型都采用精确变量来表示未知量,但在一定时期内,投入产出量具有不确定性,故考虑用模糊n-cell数来表示这种不确定量是可行的。

3.2 模糊非线性投入产出模型的建立

将在非线性IO模型的基础上,建立模糊非线性IO模型。设u(i)表示第i个部门的总投入,w(i)表示外部需求,pij(u(j))表示直接消耗系数,记第i部门对第j部门的投入μij(u(j))=pij(u(j))u(j),其中u(i),w(i),pij(u(j)),μij(u(j))∈E1,i,j=1,2,3,…,n。 由引理1知,对于u(i),w(i)表示的模糊向量,可存在唯一u,w∈L(En),使得u=(u(1),u(2),…,u(n))T,w=(w(1),w(2),…,w(n))T,再将直接消耗系数矩阵记为P(u)=(pij(u(j)))n×n,并假设P(u)中的元素均为单调的,则模糊非线性IO模型表示为

u=P(u)u+w

(18)

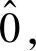
u=P1(u)u+P2(u)u+w

(19)

构造映射T:L(En)×L(En)→L(En)使得对任意的(u,v)∈L(En)×L(En),u,v非负,有T(u,v)=P1(u)u+P2(v)u+w,由定义6知T为混合单调的,于是(19)式代换为

u=T(u,u)

(20)

即模糊非线性IO模型(18)解的存在性问题转换为混合单调映射T的不动点存在性问题(20)。不妨选取初始投入向量u0,v0∈L(En),并假设u0≤v0。

3.3 模型解的存在性

对于上述构造的模糊映射T,由定理1,2,3可依次得到如下结论1～3。

结论1表明函数T(u,v)在满足一定的条件下能够使得T存在耦合不动点,但由于耦合不动点只能说明T在第一分量上达到平衡,并不等价于一般的不动点形式,因此需要赋予T更强的条件。不妨通过构造迭代格式un=T(un-1,vn-1),vn=T(vn-1,un-1),n=1,2,3,…得到序列{un},{vn}。

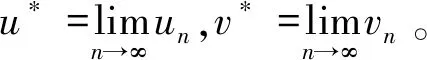
结论2表明在假设T具有紧性的条件下,可通过迭代格式来逼近T的耦合不动点。

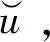
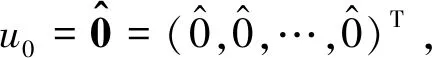
T(u0,v0)=w≥u0,

且

由结论3可知本结论成立。

证毕。