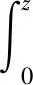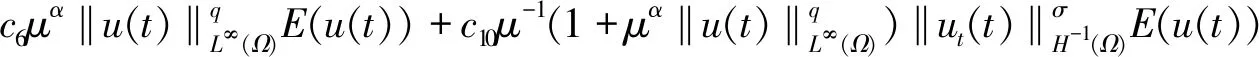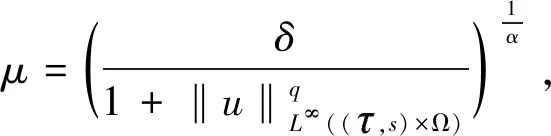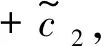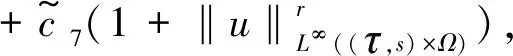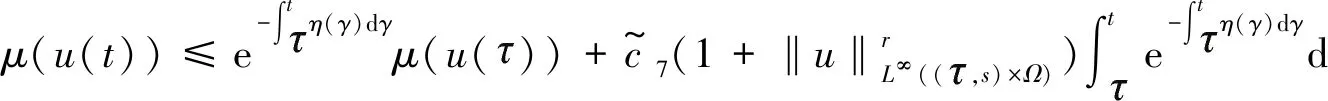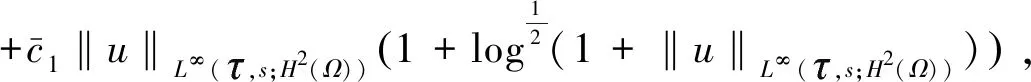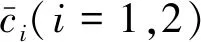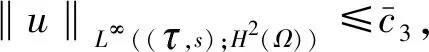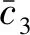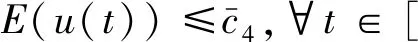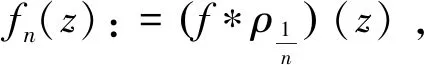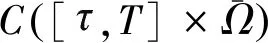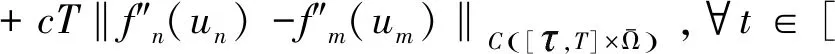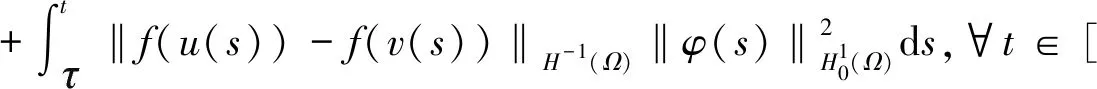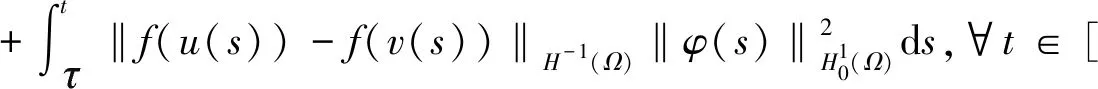带时间依赖惯性系数的Cahn-Hilliard方程的适定性
刘生清,姜金平,任丽宇
(延安大学数学与计算机科学学院, 陕西 延安 716000)
0 引言
2008年,Galenko P等[1]提出了含惯性项的Cahn-Hilliard方程,由于惯性项的加入使得方程从抛物方程变成了双曲方程;2018年,Khanmamedov A等[2]讨论在相应的初边值条件下弱解的适定性,并证明了整体吸引子的的存在性;在此基础上,丁蓉等[3]、史苑等[4]研究了带有惯性项的Cahn-Hilliard方程光滑解的存在性和爆破行为以及弱解的适定性问题;文献[5-8]中估计了具有惯性项的黏性Cahn-Hilliard方程解和指数吸引子问题。2014年,Contin等[9]基于Pata提出的时间依赖吸引子的概念给出了有界域上证明耗散性偏微分方程时间依赖全局吸引子的方法;马巧珍等[10]用此方法分别证明了带线性记忆的波方程时间依赖渐近行为和梁方程的时间依赖吸引子存在性问题;2021,年刘迪等[12]研究了带时间依赖扩散系数的分数阶非经典扩散方程的适定性。近年来,很多研究者对Cahn-Hilliard方程产生了浓厚的兴趣,目前关于带惯性项的Cahn-Hilliard方程研究已有很多,但是对于惯性项系数为依赖于时间的函数的研究还鲜少有相关文献,本文中研究亚三次非线性条件下,惯性项系数依赖于时间的Cahn-Hilliard方程解的适定性。
考虑如下带有时间依赖惯性系数的Cahn-Hilliard方程的适定性。
(1)
其中,Ω是2中具有光滑边界∂Ω的有界正则域,h∈L2(Ω)且非线性函数f满足下列条件:
f∈C2(),|f″(x)|≤C(1+|x|p),∀x∈,p<1
(2)
(3)
(4)
时间依赖的惯性系数ε(t)是非负递减的函数,满足
(5)
且存在常数L>0,使得
(6)
当ε(t)为不依赖于时间t的函数而为ε>0的常系数时方程为一般的带惯性项的Cahn-Hilliard方程。
1 基本假设



注1[2]对任意的f∈C3(),且具有增长条件
|f‴|≤C(1+|x|p),∀x∈,p<1
(7)
该条件为(4)中当α=1时的情况。
注2若u(x,t)是方程(1)的弱解,我们有
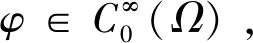
ε(t)utt+ut+Δ2u-Δf(u)=h(x)
(8)

在文献[13]中定义两个算子γ0和γ1,满足以下性质
γ0(v)是HΔ(Ω):={u∈L2(Ω):Δu∈L2(Ω)}到H-1/2(∂Ω)的线性算子,γ1(v)是HΔ(Ω):={u∈L2(Ω):Δu∈L2(Ω)}到H-3/2(∂Ω)的线性连续算子。







引理1[2]设g∈C1(),且
|g(x)≤M(1+|x|p)|,∀x∈
(9)
(10)
其中p<1,0≤q<α≤1,M≥1且r≥1。
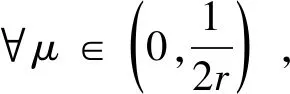
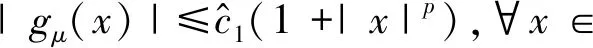
(11)
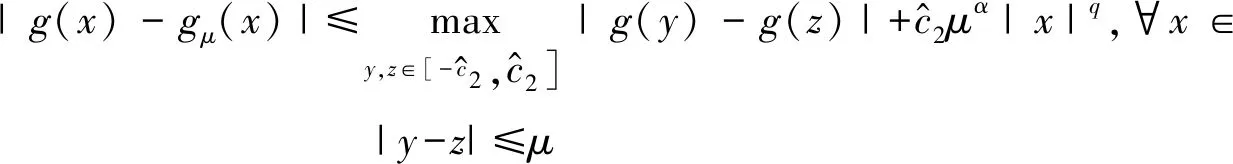
(12)
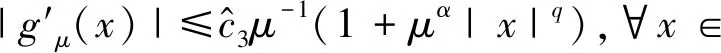
(13)
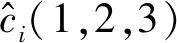
引理2[2]设f∈C2(),且
其中α>o,q≥0,M≥1且r≥1。则有以下不等式成立
其中fμ(x)=(f*ρμ)(x)。
2 弱解的适定性
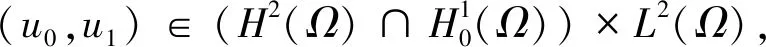
‖u(t)‖H2(Ω)+ε(t)‖ut(t)‖L2(Ω)≤c1(‖(u0,u1)‖H2(Ω)×L2(Ω)),∀t≥0,
其中c1是→上的一个非减函数。
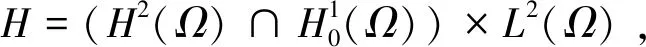

(14)


+(F(u(t)-f(0)u(t),1)-(h,(-Δ)-1u(t)))
-(h,(-Δ)-1u(s)),0≤s≤t (15) (16) 其中Q:+→+是非减函数。 下面将(1)式乘以2ut+δu并在Ω上进行积分,得 =(f″(u(t))ut(t),|▽u(t)|2) (17) 由(2)式,(16)式及H1/2(Ω)L2(Ω)得 ≤c2‖u(t)‖H2(Ω)‖u(t)‖H1(Ω) ≤c3‖u(t)‖H2(Ω) (18) 结合式(17),令δ足够小,且由于条件(5)~(6)ε(t)为非负的递减函数,得到 (19) 其中 μ(u(t))=E(u(t))+(f′(u(t)),|▽u(t)|2)+δε(t)(ut(t),u(t)). 下面估计式(19)右边,利用引理1,令g(z):=f″(z)根据式(2)和式(4),函数g(z)满足引理1的条件,则有下列式子成立 |(f″(u(t))ut(t),|▽u(t)|2)|=|(g(u(t))ut(t),|▽u(t)|2)| 有相关调查研究表明,动物及其产品质量的高低,与动物的健康状况有密切的联系,与我国疫病控制的效果有较大的关联。加强对动物疫病的监测,一方面能降低动物发生疫病的概率;另一方面还能促使动物的生产以及养殖过程得到控制,进而提升动物及其产品的质量。开展动物疫病监测工作,能保证安全的动物及其产品进入到市场,使人们都能吃到放心的产品。如对于牛羊布鲁氏等一些隐性的病菌,寻常的检测手段难以发觉,但是通过动物疫病监测以及对采样的方式,能及时发现其血液中所存在的病害,警醒防疫机构,使其提前做好防疫准备,并及时制止该肉制品流入到市场,有效保护了人们群众的人身安全。 ≤((g(u(t))-gμ(u(t)))ut(t),|▽u(t)|2)+|(gμ(u(t))ut(t),|▽u(t)|2)|, 其中gμ(z)=(g*ρμ)。 即由文献[4]可知 (20) 其中∈σ(0,1),根据式(19),当μ足够小时,得到 (21) (22) 则 (23) 因为r∈(0,1),当σ∈(r,1)时,由式(16) (24) 其中δ>0。 其中k>0,令R=‖v‖H2(Ω),得 结合式(16)得 (25) 结合式(23)~(25)可得 (26) 由式(22)、(26)可以得出 最后估计式(26)得 因此,当Tmax=∞时上式也成立。 (27) E(un(t))≤M,∀t≥0 (28) 其中M与‖(u0,u1)‖H1有关,与n无关。 令下列成立 (29) ε(t)(un-um)tt+(un-um)t+Δ2(un-um)-Δ(fn(un)-fm(um))=0 (30) 结合式(28)得 由Gronwall’s引理,式(29)和引理2得 这里 (31) 再由式(27)得 (32) 最后,由式(28)、(31)、(32),结论得证。 (33) (34) (35) 由式(16)得 (36) 由Gronwall’s引理得,当给定初值相同时 综上所述我们证明了弱解的唯一性。