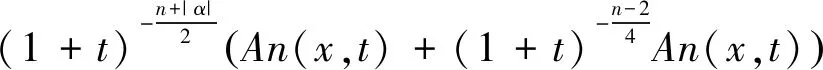粘性波动方程解的逐点估计

徐红梅,郭晓晓

(河海大学理学院,江苏 南京 211100)

0 引言

本文中考虑二维空间带粘性项非线性波动方程解的逐点估计。方程形式为

(1)

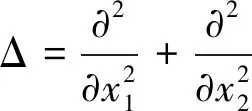
耗散波动方程能帮助我们理解流体力学中的许多复杂方程。如,带阻滞项的线性欧拉方程可转变成带阻滞项的波动方程。线性Navier-Stokes方程也可变形成(1)的线性结构。因此有很多学者研究带耗散结构的波动方程,并取得了很多成果。下面只列出带粘性项∂tΔu的波动方程的部分结果。 在文献[1-4]中,用能量估计的方法考虑了一系列拟线性波动方程在有界域中的初值问题。 文献[5]中得到了高维线性方程的Lp估计。文献[6]中结合能量估计和格林函数的方法得到非线性粘性波动方程小初值情形经典解的整体存在性和Lp估计。文献[7]中得到奇数维空间非线性方程解的逐点估计。文献[8]中考虑了空间维数n≥4且为偶数时解的逐点估计。从文献[6-8]中可以看出,方程解的衰减性与空间维数有关,维数越高,解衰减越快。所以二维空间解的逐点估计更难计算。此文中,我们由对高频格林函数和非线性项更详细的分析,解决了这一问题。

本文中,我们用C代表正常数,α是多重指标α=(α1,α2),且|α|=α1+α2,下面我们列出一些准备工作。

1 准备工作

本研究是在对(1)的格林函数作详细分析的基础上得出的。方程(1)的格林函数G1,G2为如下方程的解

直接计算得

(2)

(3)

其中

(4)

我们需要对Gi(i=1,2)分不同的频率作估计。于是定义光滑截断函数

其中2ε≤R。定义

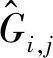
当|ξ|充分大时,由泰勒展开可得

(5)

(6)

(7)

(8)

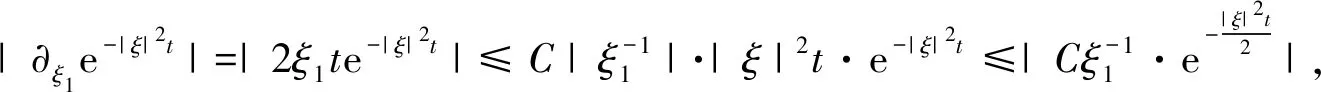
依此类推,由式(2),(5)～(6)得,当V∈Hl,对多重指标α,β,|α|≤l-2,有

≤C

(9)

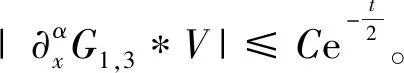
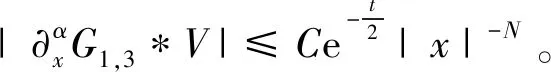
于是

(10)

同理可得,当|α|≤l,

(11)

由式(10)～(11),可得

定理1.1当V∈Hl,对任意正整数N,存在正常数C,b,有

有了这些准备,下面我们可以进入本文中的主要工作。

2 解的逐点估计

由文献[7,定理2.5]知,若式(1)有解,则解u(x,t)可表示为

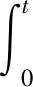
(12)

定理2.1若初值u0(x),u1(x)满足‖u0‖Hl∩W1。1≤E,u1(x)= ∂xig(x),‖g‖Hl+1∩L1≤E,且u0,u1有紧支集,对j=0,1,存在正常数CN,b,有

定理2.1的证明当u0,u1有紧支集,由文献[9,引理2.4]和[8,命题 3.1],得

由文献[9,引理2.4]和[8,命题3.2],得

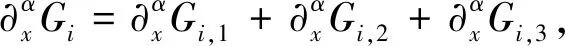
下面估计非线性项。令

由M(t)定义,当|α|≤l-3,可得

(13)

由式(1)中f(u)的形式,可得当|α|≤l-4,有

(14)

当|α|=l-3,由[6,定理1.1]和(13)式,得

(15)

为估计式(12)中的定积分,还需要知道G2,3(x,t)的构造,由文献[9,定理2.4],式(3)、(7)、(8),得

G2,3(x)=f1(x)+Cδ(x)+f2(x)

(16)

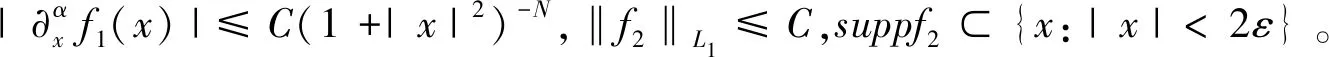
引理2.1

引理2.1的证明当|x|≥t时,有|x|-sr≥|x|-tr≥0,所以A2(x,s)≤A2(x,t)。于是

由文献[9,引理2.6],有

(17)

所以当0≤|x|≤t,有

引理得证。

引理2.2

引理2.2的证明当|x-y|<2ε,

所以

(18)

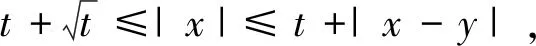
当|x|≥t+|x-y|,则|y|-tr≥|x|-tr-|x-y|≥0,于是

An(y,s)≤CAn(x,s)≤CAn(x,t).

(19)

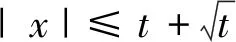
(20)

由式(18)～(20),引理得证。

引理2.3

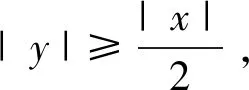
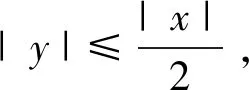
(21)

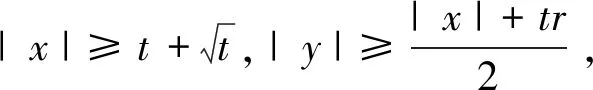
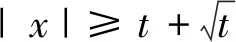
(22)

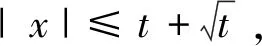
(23)

由式(21)～(23),引理得证。

由引理2.1,引理2.2,引理2.3及式(14)～(15)得,当|α|≤l-3,有

(24)

由定理2.1及式(12)、(24),当|α|≤l-3,有

其中C与E无关。由M(t)的定义,得

M(t)≤CE+M2(t)+CEM(t).

由M(0)充分小及M(t)的连续性,得M(t)有界。于是得到本文中结论。

定理2.2若方程(1)中的u0,u1满足‖u0‖Hl∩Wl,1≤E,u1(x)=∂xig(x),‖g‖Hl+1∩L1≤E,l≥4,E充分小,则方程的解u(x,t)满足