带孔扰流片核废液浓缩器强化换热数值研究*

郭俊飞,卿德藩,倪 浪,白建军,向立平

(1.南华大学 机械工程学院,湖南 衡阳 421001; 2.南华大学 核科学技术学院,湖南 衡阳 421001)

0 引 言

为应对全球气候变化问题并体现大国责任与担当,习近平总书记提出了“碳达峰,碳中和”的战略目标,也称“双碳”目标。我国能源系统要在“双碳”目标下,实现向清洁低碳的转变和发展。因此,必须尽快达到能源消耗高峰,以加快清洁能源取缔化石能源的步伐[1]。

核能作为低碳清洁能源,因其能量密度高、清洁环保、占地面积小、受国际经济情况影响小等优点而被广泛应用在核能发电、核能制氢、区域供热、海水淡化等领域。但是工业上热能转化为电能的效率一般只有33%左右。提高热电转化率在人均能源极度匮乏的中国有巨大的实际意义[2-3]。

随着我国核工业的发展,如何有效处理核工业中产生的大量放射性废水成为一大难题。这一问题不仅关乎核工业的可持续发展,而且对环境保护和维护公众健康都具有重大意义[4]。

螺旋板式换热器具有结构简单、热性能好、不易结垢等优势,是常见的放射性废液蒸发浓缩设备。其主要换热结构为两块相互呈螺旋形卷制焊接在一起的金属板和板间的环形通道[5-7]。扰流片作为常见的扰流元件,不仅起到了支撑作用,还影响着换热器的传热效率。在国内外的研究中,通过合理改进换热器通道内扰流元件的结构和型式来强化换热效果已经变得非常常见[8]。

目前众多学者对换热器的结构改进和强化传热作了研究。甘刘意等[9-10]利用数值模拟软件得到了不同Re下新型高效缩放板式换热器和普通的螺旋板式换热器性能参数的比较。李闯等[11-12]研究了多个结构参数下换热器换热性能随结构参数的变化,并通过编程得到了最小熵产下的多目标结构优化。程友良等[13]在周期流模型下,研究了不同曲率的螺旋形扰流体对流道强化传热的影响。Taher等[14-16]用实验设计结合数值仿真,分析了管壳式换热器壳程流动换热性能受不同折流板结构形式的影响。可拆式螺旋板换热器换热效率不及一般的螺板换热器,换热效率极大地限制了其在工业中的应用。

笔者基于螺旋折流板强化传热的结构展开研究。采用带孔扰流片代替普通螺旋板式换热器定距柱的支撑结构。通过FLUENT软件模拟,得到不同结构参数下带孔扰流片流道模型内传热性能因子和综合性能评价系数随Re的变化规律,从而得到最优的换热结构。为螺板换热强化传热技术及其结构优化提供一定参考。

1 相关参数的计算及定义

流道的当量直径de定义为:

(1)

式中:A为环形流道截面面积,m2;C为环形流道截面周长,m。

取入口速度u为特征速度。入口处雷诺数计算式为:

(2)

式中:ν为流体的运动黏度,m2/s。

通道努塞尔数Nu计算式为:

(3)

式中:λ为流体导热系数,W/m2K;Δtm为进出口温度的对数平均温度,K;q为热流密度W/m2。

无量纲努塞尔数Nue定义为:

(4)

式中:Nu0为普通螺旋板流道的努塞尔数。

流道阻力因子f计算式为:

(5)

式中:H为流道长度,m;ΔP为进出口压差,Pa;ρ为流体密度,kg/m3。

定义无量纲阻力因子fe计算式为:

(6)

式中:f0为普通螺旋板流道的阻力因子。

定义无量纲长度le计算式为:

(7)

式中:L为扰流片长度,m;D为扰流片间距,m。

2 物理与数学模型

2.1 物理模型

忽略带孔扰流片蒸发器进出段的影响。当主流方向的扰流片超过一定的数目之后,流道内流体的运动形式不断地周期性重复。流体的运动进入周期性充分发展阶段。因此,模拟采用周期流模型,选择螺板换热器中的一段环形通道作为研究对象。根据相似理论,以该段流道的流动和传热特性代表整个换热通道的特征。建模区域示意图如图1所示,虚线内为流道建模区域。图中,L为扰流片长度,D为间距,R为孔径,具体结构参数如表1所列。

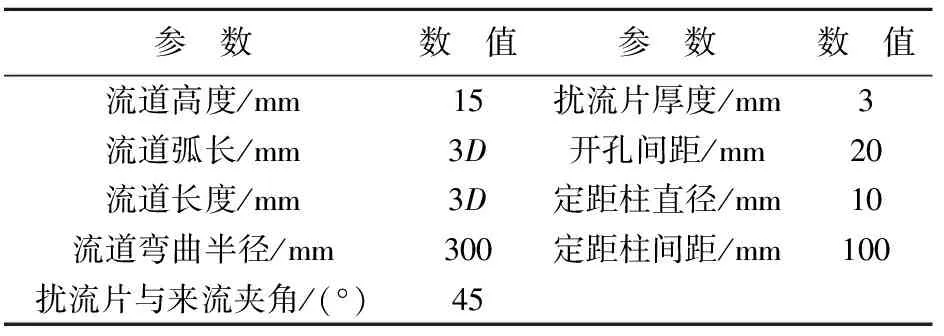
表1 流道结构参数

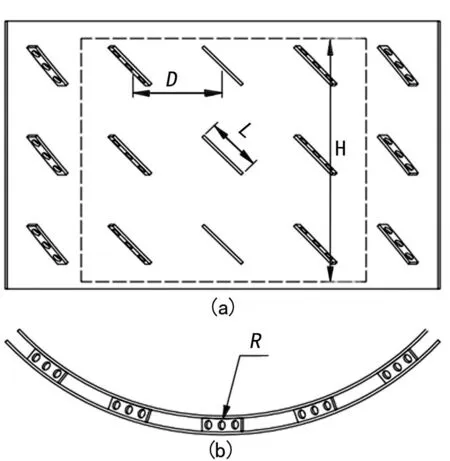
图1 建模区域示意图

根据表1的流道结构参数,利用三维建模软件建立2种流道模型,其几何模型如图2所示。

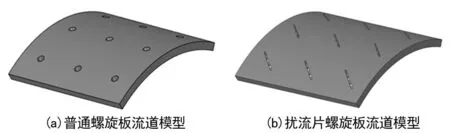
图2 流道模型

2.2 物理模型的简化

由于带孔扰流片的阻碍作用,流道内流动换热过程十分复杂。因此,对模拟过程中的几何模型和流场特性作如下简化假设。

(1) 假设流道中的介质为均匀、连续、不发生相变的不可压缩流体。

(2) 假设流体本身的物性参数(密度、比热容、导热系数)是常数。

(3) 忽略由密度差引起的浮升力、重力、污垢热阻、换热壁面与扰流片之间的接触热阻、流体流动时黏性耗散作用所产生的热效应。

(4) 假设环形通道进口处的速度和温度分布均匀。

2.3 基本控制方程

通道内的流动换热过程满足质量守恒方程、动量守恒方程和能量守恒方程三个基本控制方程,方程表达如下。

(1) 质量守恒方程

(8)

(2) 动量守恒方程

(9)

(10)

(11)

(3) 能量守恒方程

(12)

2.4 边界条件

流体选用某工厂放射废液;进口处设定为速度入口,给定温度300 K;设置换热壁面、扰流片表面为无滑移壁面,恒定壁温370 K;出口处设置为outflow;两侧为周期边界条件,如图3所示。

图3 边界条件

2.5 数值方法设置

在fluent meshing中对该流道模型划分非结构化网格,并按图3设置边界条件。利用FLUENT软件进行求解。选择收敛速度更快的SIMPLEC算法进行压力速度的耦合。该算法求解复杂流场问题时有比较好的效果。湍流模型选择适用性更广泛的realizable k-ε模型[17],该模型能够较好地计算旋转流场。壁面处采用增强壁面。控制方程都采用二阶迎风格式[18-19],残差收敛精度设定为10-6。

2.6 网格划分及其独立性分析

为检验模型的网格无关性,建立四种不同网格数量的几何模型。其网格数量分别为95 万、176 万、275 万和403 万。用Nu作为不同网格数下流道的评价标准。

模拟结果如图4所示。275 万和403 万网格的计算结果误差仅相差1.7%。因此,在确保模拟结果可靠的基础上充分利用计算机的计算资源,选择模型网格数为275 万。

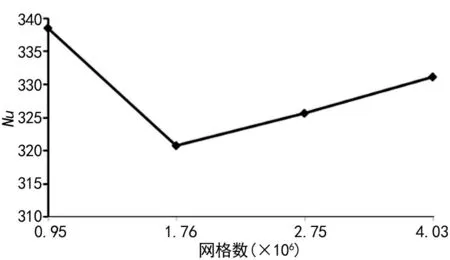
图4 网格独立性分析

2.7 模型及算法正确性验证

为检验文章模型及算法选择的准确性,采用文中的算法对文献[20]中的可拆式螺旋板式换热器模型进行数值模拟。

验证模型的结构参数如下:定距柱排列方式为正三角形排列,定距柱间隔120 mm,换热板厚3 mm,换热器通道总长400 mm,流道宽15 mm。

由文献[20]的实验研究可知,可拆式螺板换热器在水-水系统下做湍流运动时,通道对流换热系数计算如下所列:

(13)

将式(13)计算的对流传热系数与数值模拟结果进行对比,如图5所示。

图5 模拟值与实验值对比

由图5可知,采用realizablek-ε模型、增强壁面函数法计算出来的对流传热系数与实验拟合公式(13)中得出的对流换热系数误差在合理范围内。最大误差为11.7%,说明文章选择的模型和算法是可行的。

3 模拟结果及分析

3.1 流场分析

入口速度为1 m/s,L=60 mm,D=100 mm,分别取R=0 mm和R=10 mm的环形通道为研究对象。该结构参数下流线的轨迹如图6所示。

图6 流线图

从图中可以看到,扰流片结构对流体的流动方向和速度大小都产生了影响。扰流片周围产生的涡流将流体边界层冲刷得更薄,强化了对流换热效果。而且流体的冲刷作用使通道内流体的流动情况变得更加复杂,增大了流体流动的紊乱程度,亦提高了流道的传热系数。开孔对流动的影响主要是改变了流体的流动形式[21]。

3.2 扰流片结构参数对传热性能因子的影响

3.2.1 长度和间距对传热性能因子的影响

常用的换热器换热性能评价方法有单一性能评价法、基于热力学第二定律的性能评价法、综合性能评价法等。单一性能评价法用流道内压降或换热系数等作为评价指标对换热器性能进行评价。由于单一性能评价法简单易懂,因此在工程中应用较为广泛。而以热力学第二定律为基础的评价法因其计算式十分复杂,而且得到的结果无明确物理意义、难以分析而在工程上应用较少。

基于强化换热技术的结构优化通常都是以增大泵功为代价达到的,并且泵功增大的程度一般大于换热系数的增幅。因此,选择同时考虑了压力损失和换热系数的综合性能评价系数较为合理。

文章综合性能评价系数采用等泵功约束评价准则计算,其计算式为:

(14)

图7给出了D=100 mm且未开孔时,不同扰流片长度下Nu数随Re的变化关系。

图7 不同扰流片长度下Nu随Re变化

图8为无量纲长度le=0.6且未开孔时,不同扰流片间距下Nu数随Re的变化关系。

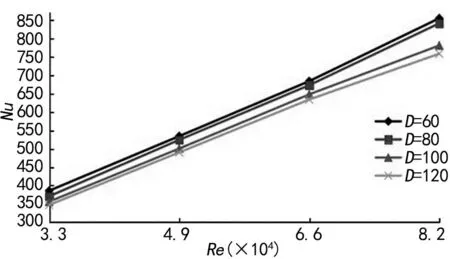
图8 不同扰流片间距下Nu随Re变化

由图7～8可知,在不同扰流片长度和间距下,流道内的Nu均随着Re的增大而增加。在相同Re下,Nu随扰流片长度的增加而增大,且其变化的程度先急后缓。L值在40～60 mm的范围内变化最为剧烈,平均变化率为6%,L值在80～100 mm的范围间变化最小,平均变化率仅为1.2%。Nu随扰流片间距的增加而减小,且其变化的程度先剧烈后平缓,D值80～100 mm的范围内变化最为剧烈,平均变化率为5%。

不同扰流片长度时阻力因子随Re的变化关系和不同扰流片间距下f随Re的变化关系如图9～10所示。

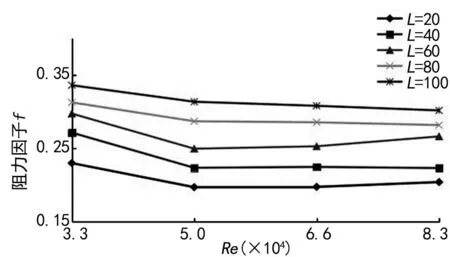
图9 不同扰流片长度下f随Re变化

图10 不同扰流片间距下f随Re变化

从图9、10可以看出,在不同扰流板结构参数下,阻力因子均随Re的增大有下降的趋势,其下降的趋势由快到慢。

在同一Re下,f随着扰流片长度的增加逐渐增加,其平均增长率为11%;f随着扰流片间距的增大而逐渐降低,在扰流片间距增大的过程中,阻力因子的变化先快后慢,其最大变化率为27.5%。由此可见,采取增加扰流片长度来强化换热虽然在一定程度上增加了换热效率,但是压降也几乎呈直线增加。增加扰流片的间距会减小Nu数,也会降低换热过程的压降。

3.2.2 孔径对传热性能因子的影响

图11为L=60 mm、D=100 mm时,Nu、f在不同孔径下随Re的变化。

图11 不同开孔直径下Nu、f随Re的变化

从图中可以看出,随着孔径的增大,流道内的Nu、f都呈现先增后减的趋势,R值为0～14 mm,Nu和f的平均变化率分别为8.1%和27.3%。这是因为增大开孔会使通道内流体由近似螺旋流转变为直线流动,减小换热系数。开孔又会一定程度上增加流体的紊乱程度,增大换热系数。小孔径通道内流体流速降低,会增大动压的损失。当孔径增大引起的流动阻力减小大于其影响流速导致的阻力增加时,通道内总体的f开始降低。

3.3 综合性能分析

不同扰流片结构参数下的综合性能评价系数如图12～13所示。

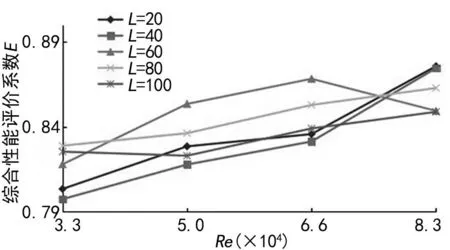
图12 不同扰流片长度下E随Re变化

图13 不同扰流片间距下E随Re变化

从图12～13中可以看出,当D=100 mm时,E随Re的增加呈线性增长,并且随着扰流板长度的增加先增后减。这是由于当流道内Re较大时,扰流片长度的增加不再是决定强化传热效果的主要因素,进口处流速的增大使通道内流体紊乱程度更大。流速引起的换热系数增幅要大于扰流片长度的增幅,且长度增加又会引起阻力损失的增大。所以当Re较大时扰流片长度短的模型综合性能系数更高。

当le=0.6,扰流片间距小于80 mm时,E随Re的增加而增大,当扰流片间距再增大时,E随Re的增大先增后减。这是因为扰流片间距增大时,会引起压降和换热系数的降低,但是压降减小的幅度更大。

不同孔径下综合性能评价系数的变化如图14所示。

图14 不同开孔直径下E随Re的变化

开孔结构下,随着Re的提高,E有降低的趋势。随着孔径增大,综合性能系数的变化呈先减后增的趋势,这是由于开孔引起的压降和换热系数共同变化导致的。在L=60 mm、D=100 mm时,Re在33 238～49 858的范围内开孔13 mm的综合性能更好,Re大于49 858时,未开孔扰流片的综合性能更佳。

4 结 论

文中重点采用周期流边界条件研究不同结构参数的带孔扰流板对螺板换热压降和换热性能的影响。得到了最大综合性能评价系数下的最优结构参数,所得结论如下。

(1) 采用周期流模型可以较准确地计算带孔扰流片流道内的流动和传热问题,得到的模拟结果与基于实验获得的对流传热拟合公式的计算值吻合良好,最大误差为11.7%。

(2)Nu随着扰流片长度的增加依次递增,随着间距的增加递减。阻力因子也随扰流片长度的增加逐渐增大,随着间距的增加而减小。大孔径能较大地降低通道内的阻力损失,增大综合性能评价系数。

(3)Re小于66 477时,开孔直径大的扰流片综合性能系数大,Re再增大时,未开孔的综合性能系数更大。研究不同Re数下的最优结构参数有利于之后该优化结构下的多目标优化问题的研究,可为螺板换热器强化换热及其工业应用提供参考和借鉴。