扰流片式推力矢量喷管气动特性数值模拟研究

丛戎飞, 吴军强, 张长丰, 叶友达

(1. 中国空气动力研究与发展中心 高速空气动力研究所, 绵阳 621000;2. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000;3. 国家计算流体力学实验室, 北京 100191)

0 引 言

扰流片式推力矢量控制技术是通过将扰流片插入发动机尾喷流，利用扰流片上游的边界层分离以及激波边界层干扰等复杂的流动现象，使喷流相对喷管轴线发生偏转来实现推力矢量控制。扰流片在未工作时位于尾喷流外缘，不接触高温燃气，从而可以避免产生推力损失，减轻扰流片烧蚀。扰流片式推力矢量控制技术较为独特，目前仅有俄罗斯的R-73导弹(图1)及其衍生型号采用了这种控制方式。与目前先进空空导弹普遍采用的燃气舵相比，扰流片具有非作用时无附加推力损失、响应快、控制力较大等突出优点，推力矢量角最大可达14°，在空空导弹、垂直发射导弹、以及弹射座椅等领域都具有广阔的应用潜力[2-4]。 20世纪60年代起，Hollstein H J、Eatough R G等人针对扰流片式推力矢量控制技术进行了一系列冷喷流和燃气喷流试验，研究了扰流片形状、安装位置以及扰流片与喷管出口间隙对于侧向力和推力 损失等参数的影响，为扰流片的工程应用奠定了理论基础[5-9]。国内对于扰流片式推力矢量控制技术的研究起步较晚，研究手段以数值模拟为主，并进行了部分静态及动态试验研究[10-13]。

图1 R-73导弹推力矢量控制系统Fig.1 Thrust vector control system of R-73 missile

目前国内针对该技术的研究尚停留在原理验证以及有效性评估阶段，与工程实用之间还有一定距离。为了满足工程应用中对推力矢量喷管控制率建模以及优化设计的需求，本文将通过数值模拟手段，针对圆形、弧顶矩形以及扇形这三种扰流片外形，系统性的研究扰流片几何形状对喷管推力矢量特性的影响规律，建立气动数据库，为该项技术的工程化提供参考，为扰流片气动优化设计做铺垫。

1 扰流片式推力矢量控制技术原理

扰流片上游流场结构如图2所示。当扰流片伸入喷管出口流场时，将会阻塞部分出口面积，直接导致在喷管的扩张段内产生斜激波，并伴随有边界层分离，而激波后分离区的压力远远大于扰动前的压力，将会在喷管内壁面产生非对称压力分布，从而产生侧向力[14]。而斜激波与弓形激波在扰流片迎风面形成高压区，使扰流片受到了与喷管推力方向相反的作用力，从而引起了喷管的推力损失。

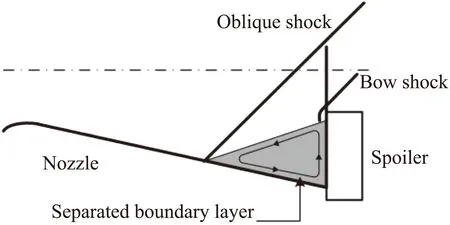
图2 流场结构示意图Fig.2 Shock profile

推力矢量分析如图3所示。FAO为扰流片未插入时的初始轴向推力。FR为扰流片插入后的总推力，FA为轴向推力，FS为侧向力。将总推力FR与喷管轴线的夹角θ定义为推力矢量角，可表示为：

同时，为了评估扰流片引起的推力损失，定义推力损失系数η：

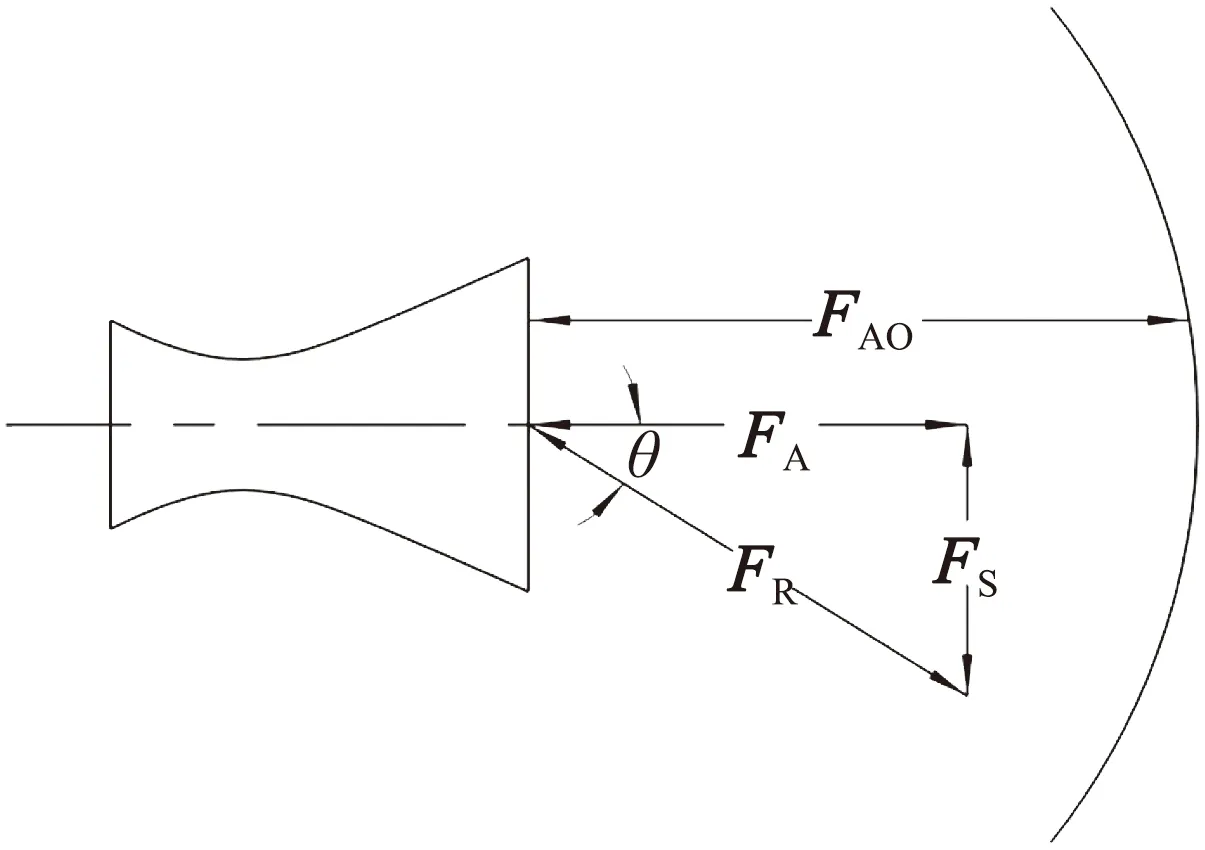
图3 推力矢量分析Fig.3 Force relationship

推力矢量角描述了扰流片产生的侧向控制力的大小，推力损失系数描述了扰流片工作时引起的推力损失的大小。本文将选取推力矢量角及推力损失系数作为衡量推力矢量特性的主要参数，对数值模拟结果进行分析和评估。在进行扰流片设计时，应使这两个参数满足侧向控制力以及及推力的需求。

喷管的推力矢量通过公式(3)进行计算。

F=∑[ρv(v·N)+(p-p∞)N]ΔA(3)

其中:v为出口截面微元处燃气的平均速度，p为出口截面微元的平均压强，p∞为环境大气压强，N为出口截面微元的单位矢量。

2 数值模拟方法与验证

2.1 数值模拟方法

使用计算流体力学商业软件Fluent进行数值模拟，选用求解雷诺平均Navier-Stockes方程的求解器；空间离散方法为有限体积法，无粘通量采用Roe格式进行离散，粘性通量采用中心差分格式离散，时间推进方法采用LU-SGS(Low Upper Symmetric Gauss Seidel)隐式方法。湍流模型采用了二方程的Realizablek-ε模型，壁面附近采用标准壁面处理[15]。

2.2 数值模拟方法验证

论文为了验证本文数值模拟方法的准确性和有效性，选取美国推进实验室的某轴对称喷管进行数值模拟。喷管膨胀面积比为6.60。入口总温为 294.3 K，落压比为10，出口为大气环境[16]。

数值模拟结果与文献[16]中试验结果的对比如图4所示。图中：p0为喷管入口总压，p为当地静压，X为横坐标，XL为喷管扩张段长度。从图中可以看出，数值模拟结果与试验结果吻合较好。

(a) 喷管轴线马赫数

(b) 喷管轴线压力

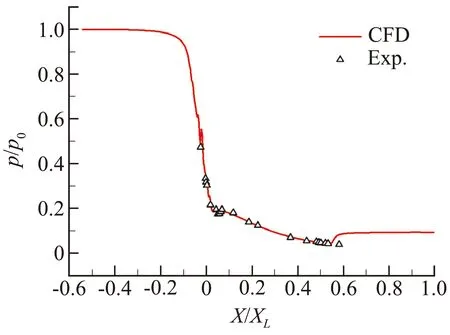
(c) 喷管壁面压力

2.3 计算模型及边界条件

数值模拟采用的基准轴对称喷管的母线形状如图5所示。喷管膨胀面积比为6.25，设计落压比NPRD=67.2。在喷管出口处添加不同形状的扰流片，即构成了简化后的扰流片式推力矢量装置几何模型。

圆形扰流片几何模型如图6所示。h为扰流片插入高度，选取h=0、2、4、6、8 mm五个状态进行数值模拟，分析扰流片插入高度h对喷管内流特性的影响。

图5 喷管母线(单位：mm)Fig.5 Sketch of the nozzle(unit: mm)

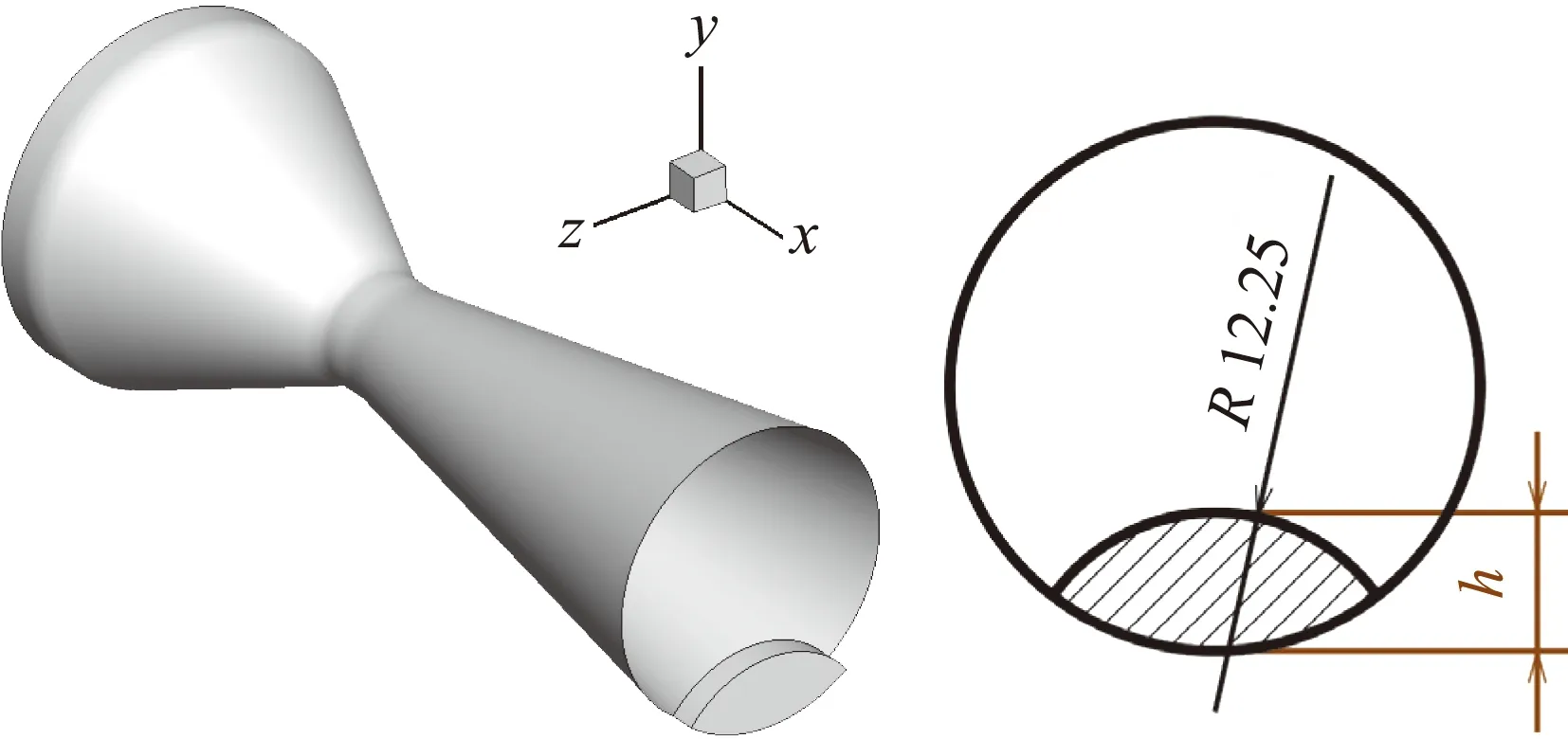
图6 圆形扰流片几何模型(单位：mm)Fig.6 Round spoiler (unit: mm)

弧顶矩形扰流片的几何模型如图7所示。扰流片的宽度d为设计变量，本文将针对不同宽度的弧顶矩形扰流片进行数值模拟。数值模拟状态见表1。

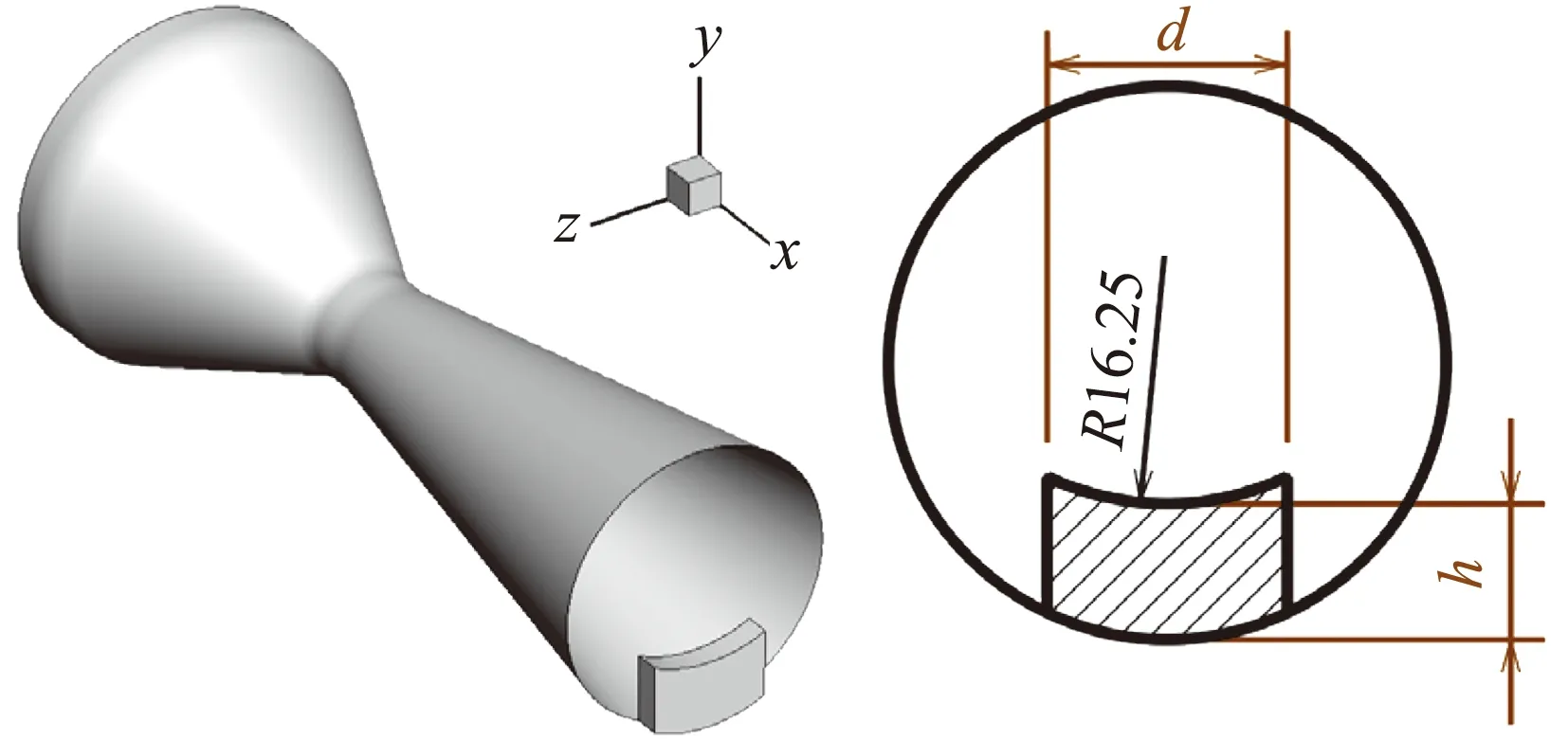
图7 弧顶矩形扰流片几何模型(单位：mm)Fig.7 Rectangle spoiler (unit: mm)

d/mmh/mmd/mmh/mmNo.1102No.7146No.2104No.8148No.3106No.9182No.4108No.10184No.5142No.11186No.6144No.12188

扇形扰流片的几何模型如图8所示。扇环形对应的弧心角为90°。扇形扰流片底部圆弧和顶部圆弧半径相同，顶部圆弧圆心到扇形顶点的距离l为设计参数，通过改变l获得不同形状的扰流片。数值模拟状态见表2。

边界条件设置如图9所示，喷管入口燃气假设为理想可压缩气体，入口边界条件为压力入口，总压p0=7.2 MPa，总温T0=2.2×103K；喷管壁面为绝热无滑移壁面；远场边界条件为压力远场，外流来流马赫数Ma∞=2.96，环境大气压p∞=101 325 Pa，环境温度T∞=300 K。

图8 扇形扰流片几何模型(单位: mm)Fig.8 Sector spoiler (unit: mm)

l/mmh/mml/mmh/mmNo.162No.788No.264No.8102No.366No.9104No.482No.10106No.584No.11108No.686No.121010

图9 边界条件Fig.9 Boundary conditions

3 计算结果分析

3.1 圆形扰流片

圆形扰流片上游喷管壁面静压分布如图10所示。壁面静压在边界层分离点受激波边界层干扰的作用发生跃升，然后在主流的膨胀作用下逐渐下降，最后由于扰流片顶部弓形激波的作用再次上升。

喷管对称面马赫数云图如图11所示，选取h=4 mm、6 mm、8 mm三个状态进行对比。由于扰流片阻碍了流体的流动，在扰流片上游出现了边界层分离，并在分离点诱导出了一道斜激波，分离区的高压在喷管扩散段壁面上的积分量就是扰流片式推力矢量装置侧向控制力的来源。同时在扰流片顶部有一道弓形激波，使位于激波后的扰流片迎风面存在高压区，使扰流片受到了与喷管推力方向相反的作用力，从而引起了喷管的推力损失。随着插入高度的增加，扰流片对喷流的阻碍作用增强，边界层分离点前移，同时扰流片顶部弓形激波的强度增加。

图10 喷管壁面静压分布Fig.10 Pressure distribution at the nozzle wall

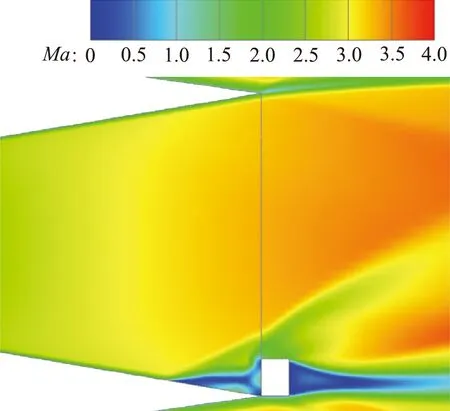
(a) h=4 mm

(b) h=6 mm

(c) h=8 mm

图12给出了圆形扰流片产生的推力矢量角及推力损失随插入高度的变化曲线。推力矢量角与推力损失都随着扰流片插入高度的增加而增加，但呈非线性关系。这是由于扰流片形状为圆形，其堵塞喷管的有效面积随插入高度增加而呈非线性增长。

图12 圆形扰流片推力矢量特性曲线Fig.12 Thrust vector performance of round spoiler

3.2 弧顶矩形扰流片

图13给出了三组插入高度相同但宽度不同的弧顶矩形扰流片上游喷管壁面静压分布对比曲线图。在扰流片插入高度相同的情况下，扰流片越宽，边界层分离点就越靠前。这是由于随着扰流片变宽，其堵塞喷管的有效面积增大，使扰流片上游的逆压梯度增高。同时，随着扰流片变宽，喷管出口处壁面压力的峰值逐渐降低。这是由于分离点前移，分离区范围越大，扰流片顶部距离主流区越远，而扰流片顶部弓形激波强度越低。

图13 弧顶矩形扰流片上游喷管壁面静压分布Fig.13 Pressure distribution at the nozzle wall

喷管出口截面静压分布如图14所示。扰流片迎风面顶部由于斜激波及弓形激波后气流的作用而产生一个高压区，即图中红色区域。随着扰流片宽度增加，顶部高压区的周向(宽度方向)范围增加，而径向(高度方向)范围减小，故高压区面积随扰流片宽度变化较小。由于扰流片高压区是产生推力损失的主要原因，推力损失的值与高压区面积相关，因而可以推断推力损失随扰流片宽度变化较小。

图15给出了三组不同宽度的弧顶矩形扰流片的推力矢量特性曲线。由图15(a)可知，随扰流片插入高度增加，推力矢量角增大。而在插入高度一定时，随着扰流片宽度增加，推力矢量角也随之增大。因而对于弧顶矩形扰流片而言，推力矢量角受扰流片高度及宽度的共同影响。而由图15(b)可知，推力损失系数对扰流片宽度变化不敏感，其大小主要取决于扰流片插入高度。由图15(c)可知，在产生的推力矢量角相同时，越宽的扰流片产生的推力损失越小，其中d=18 mm的弧顶矩形扰流片推力损失最小。对于同样产生推力矢量角约为5.5°的工况，增大扰流片宽度可以使推力损失从5.4%降至3.4%。因此，对于矩形扰流片而言，可以通过增大扰流片宽度的方式减小推力损失，提高控制效率。

(a) d=10 mm，h=8 mm

(b) d=14 mm，h=8 mm

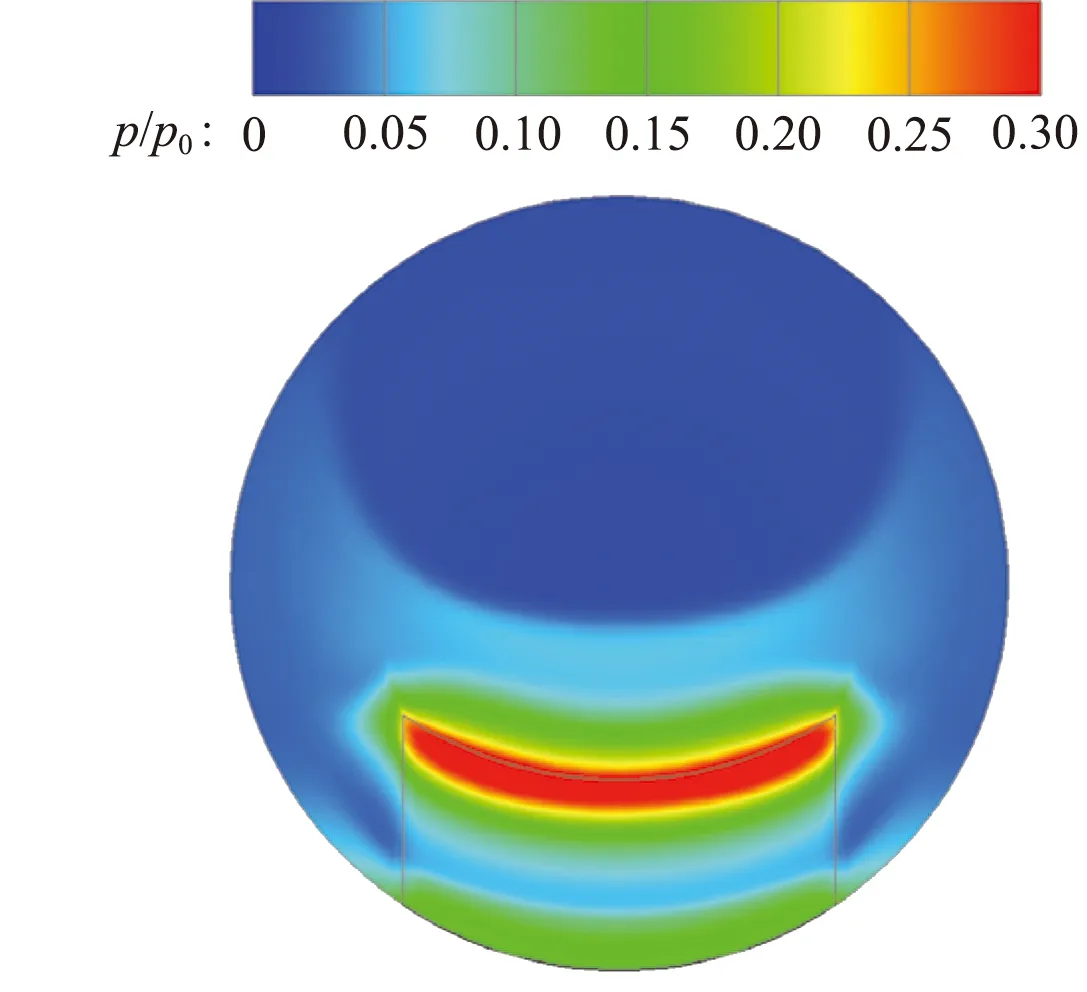
(c) d=18 mm，h=8 mm

3.3 扇形扰流片

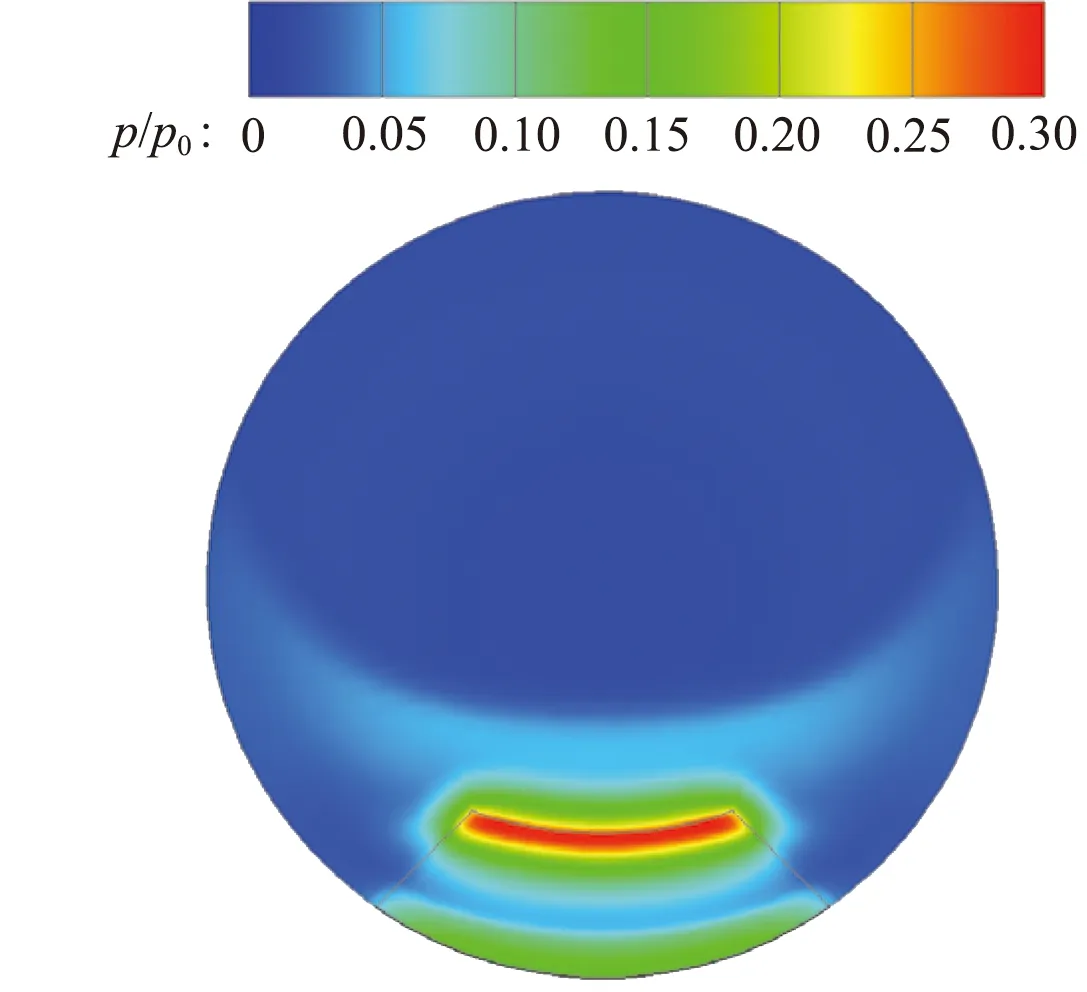
喷管出口截面静压分布如图16所示。扇形扰流片在插入高度一定的前提下，随着l的增加，顶部高压区周向范围减小，而径向范围增加，导致推力损失随l变化较小。

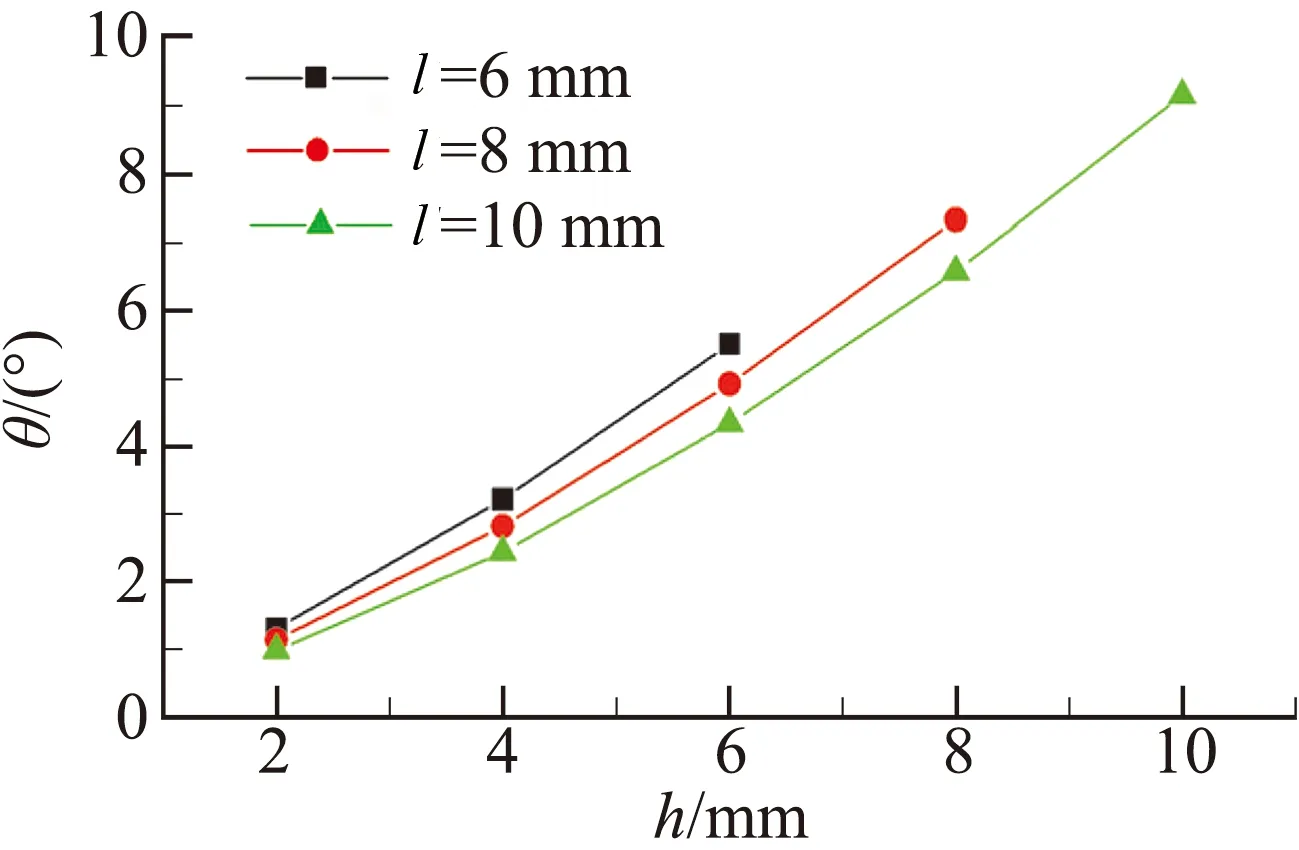
图17给出了不同l(顶部圆弧圆心到扇形顶点的距离)的三组扇形扰流片的推力矢量特性曲线。

由图17(a)可知，在参数l一定时，推力矢量角随扰流片插入高度增加而增加，而在扰流片插入高度一定时，推力矢量角随参数l增加而减小。即推力矢量角受扰流片插入高度以及参数l的共同影响。

如图17(b)所示，在插入高度一定时，推力损失随参数l的变化非常小，说明推力损失主要取决于扰流片插入高度。结合前文中弧顶矩形扰流片相关结论进行分析，在插入高度一定时，无论是改变扰流片宽度还是改变参数l，都会直接改变扰流片面积。因而可以初步判定对于特定形状的扰流片而言，在插入高度一定时，推力矢量角对扰流片面积变化较为敏感，而推力损失系数对扰流片面积的变化不敏感。

由图17(c)可知，在推力矢量角相同时，参数l越小的扰流片产生的推力损失越小，其中l=6 mm的扇形扰流片推力损失最小。因而对于扇形扰流片，减小参数l可以减小推力损失，提高扰流片的控制效率。

3.4 三种扰流片对比

针对上述的圆形、弧顶矩形、扇形这三种扰流片，设计扰流片面积同为s=112 mm2，插入高度同为h=8 mm的三种外形，即：扰流片半径为13.96 mm的圆形扰流片，宽度为14 mm的矩形扰流片，l=11.16 mm的扇形扰流片，并对其进行对比研究。

(a) 推力矢量角

(b) 推力损失系数

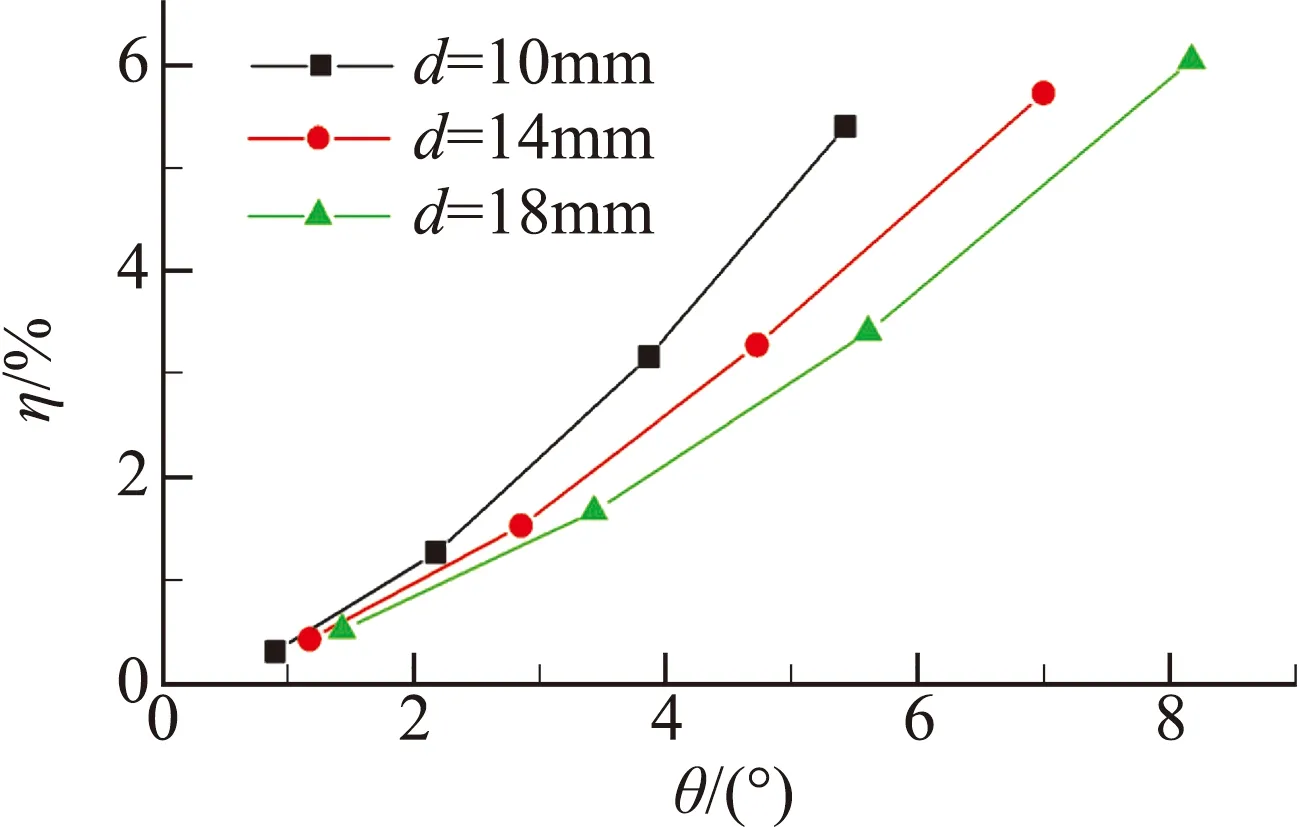
(c) 推力损失系数随推力矢量角变化

图15 弧顶矩形扰流片推力矢量特性曲线
Fig.15 Thrust vector performance of rectangle spoiler

(a) l=6 mm，h=6 mm

(b) l=8 mm，h=6 mm

(c) l=10 mm，h=6 mm

图16 喷管出口截面静压分布
Fig.16 Pressure ratio profiles at nozzle outlet plane

(a) 推力矢量角

图17 扇形扰流片推力矢量特性曲线
Fig.17 Thrust vector performance of sector spoiler

喷管出口截面静压分布如图18所示。由于几何外形不同，三种扰流片迎风面高压区的形状以及分布范围都有较大区别。由于弧顶矩形扰流片顶部较宽，其顶部高压区的周向范围较大，扇形扰流片次之，圆形扰流片高压区范围最小。因而在面积相同的情况下，弧顶矩形扰流片产生的推力损失最大，扇形扰流片次之，圆形扰流片最小。

三种扰流片的推力矢量特性如图19所示。由图19(a)可知，在扰流片面积及插入高度相同时，弧顶矩形的推力矢量角最大，圆形扰流片推力矢量角最小；由图19(b)可知，在扰流片面积及插入高度相同时，弧顶矩形的推力损失系数最大，圆形扰流片推力损失系数最小。因此，在扰流片面积及插入高度一定的前提下，几何形状对于推力矢量特性有一定影响。

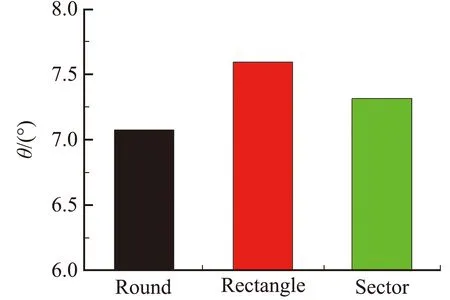
(a) 推力矢量角

(b) 推力损失系数

4 结 论

本文将通过数值模拟手段，针对圆形、弧顶矩形以及扇形这三种扰流片外形，研究了扰流片几何形状对喷管推力矢量特性的影响规律。通过对数值模拟结果的分析，得出以下结论：

(1) 推力矢量角与推力损失系数都随着扰流片插入高度的增加而增加。

(2) 斜激波和弓形激波后的气流在扰流片迎风面顶部形成了高压区，喷管推力损失的值与高压区面积相关，而高压区面积受扰流片形状影响。

(3) 对于矩形扰流片，可以通过增加扰流片宽度的方式减小推力损失，提高控制效率，对于同样产生推力矢量角约为5.5°的工况，增大扰流片宽度可以使推力损失从5.4%降至3.4%；对于扇形扰流片，可以通过减小上圆弧圆心与扇形顶点距离的方式减小推力损失，提高控制效率。

(4) 在扰流片插入高度及面积一定时，几何形状对推力矢量特性有一定影响，其中弧顶矩形扰流片的推力矢量角及推力损失均为最大，圆形扰流片均为最小。