Multi-h C波段导航信号调制方式及性能评估
倪育德 易茉涵 刘瑞华 邹 玲
(中国民航大学电子信息与自动化学院,天津 300300)
1 引言
鉴于目前全球导航卫星系统(Global Navigation Satellite System,GNSS)的信号几乎都集中在频谱拥挤的L 波段(1164~1610 MHz),国际电信联盟(International Τelecommunication Union,IΤU)2000年将C 波段中频段范围5010~5030 MHz 的部分提供给导航卫星下行信号使用[1]。C 波段导航信号频谱干扰少,电离层误差较低,能满足民用航空对高性能GNSS 的要求[2],这使研究和开发C 波段导航资源受到越来越多的重视,尤其对在现有L 波段资源中占有率明显处于劣势的北斗卫星导航系统(BeiDou Navigation Satellite System,BDS),更应该探索卫星导航服务新频段。但C 波段导航与微波着陆系统(Microwave Landing System,MLS)、射电天文业务(Radio Astronomy Service,RAS)频段相邻,由于其带宽仅为20 MHz,因此在实际应用中对频带利用率有极其严格的限制。如何在充分利用有限频谱资源的同时,兼顾信号兼容性约束和导航性能就成为C波段导航研究的焦点。
2008 年以前,欧洲学者对C 波段导航的调制方式进行了大量研究,曾提出将升余弦、最小频移键控(Minimum Shift Keying,MSK)[3]和高斯最小频移键控(Gaussian Minimum Shift Keying,GMSK)[4]等众多信号列为Galileo 卫星导航系统C 波段候选导航信号,但这些信号或在包括兼容性约束在内的性能上存在一定缺陷,或对硬件环境要求高,因此可行性存在一定困难。国内从2012 年开始见到有关C波段导航信号调制方式研究的公开报道,先后提出在C波段导航使用的调制方式主要有椭圆球面波函数(Prolate Spheroidal Wave Functions,PSWF)[2]、最小频移键控脉冲二进制编码符号调制[5]、连续相位调制(Continuous Phase Modulation,CPM)[6]以及基于PSWF 的CPM(CPM-PSWF)调制[7]等。总体而言,国内外对C 波段导航信号调制方式的研究还处在探索挖掘阶段。
1981 年,瑞典隆德大学的Aulin Τ 等人为解决相移键控调制技术造成的频谱泄露问题正式提出连续相位调制体制,并对CPM 的信号表达式、频谱特性以及误码性能在内的众多特性进行了详细阐述和总结[8-9]。针对带宽十分受限的C 波段,CPM调制由于包络恒定、相位连续、旁瓣衰减快、频带利用率高等优点成为C 波段导航信号调制的首选[10-11],但将CPM 调制应用于C 波段导航并对其基础导航性能指标进行评估的公开报道并不多见,针对多调制指数(Multi-h)CPM 应用于C 波段导航进行深入研究的报道就更少。
Multi-hCPM 是在单调制指数(Single-h)CPM基础上发展起来的,在航天遥测和卫星通信领域受到广泛关注,早在1999年,继Multi-hCPM成为先进靶场遥测体制的第二步目标之后,美国又将其纳入军用卫星通信标准之中,定义为物理层信号波形[12];2012 年,欧洲电信标准协会也将Multi-hCPM 纳入第二代数字视频广播交互式卫星系统标准之中[13]。
相比Single-hCPM,多个指数循环变化的特性使得Multi-hCPM 的频带利用率和功率效率更高,但与之对应的是接收端同步和解调难度的增加,降低接收机设计复杂度一直是Multi-hCPM 相关研究的重点。2004-2005年,美国杨百翰大学的Perrins E陆续发表两篇论文[14-15],将CPM 的脉冲幅度调制(Pulse Amplitude Modulation,PAM)表示法扩展至Multi-hCPM,给出了Multi-hCPM 系统接收端基于PAM 分解的最优解调算法和次优解调算法,并由此设计了一种最优最大似然序列估计接收机;2010年,瑞典韦克舍大学的Kulikov G V 等人提出了一种Multi-hCPM 信号调制解调器的全数字设计方案[16],在接收端使用Viterbi 算法进行联合解调、符号定时和载波同步。
2014 年,中国工程物理研究院的钟声博士围绕遥测中Multi-hCPM 同步及序列检测技术开展了深入研究[17],设计了一套Multi-hCPM 中频收发信机系统;2017 年,中国工程物理研究院的谢顺钦研究了低信噪比下Multi-hCPM 的低复杂度非相干迭代检测算法[18],有效解决了低信噪比下Multi-hCPM解调困难、复杂度高以及同步困难等问题;2020年,中国科学院国家空间科学中心的陈长龙提出一种通用的基于零中频构架的Multi-hCPM 调制系统和基于PAM分解的低复杂度解调算法[19],并根据该算法设计Multi-hCPM 序列检测器;同年,重庆大学的韦玉锋提出了一种Laurent-FPΤ-RSSD 联合解调算法,有效降低了Multi-hCPM 信号解调复杂度[20];同年,西安电子科技大学的刘蒙蒙等人设计了一种适用于Multi-hCPM 信号的导频辅助准相干解调算法[21];2021 年,电子科技大学的李之恒提出基于最大累计度量的低复杂度检测算法,用于降低Multi-hCPM信号的接收机检测复杂度[22];2022 年,南京信息工程大学的刘铭权研究和改进低密度奇偶校验码级联Multi-hCPM系统的复杂度和参数性能[23]。
2002 年,加拿大Western 大学的I.A.等人通过引入CPM 的相位相关性达到减小OFDM 应用时的误码率的目的,提出了Single-h的基于正交频分复用的CPM(CPM based on Orthogonal Frequency Division Multiplexing,OFDM-CPM)[24]。目前,仅文献[25]提出将该调制方式用于C 波段导航,但没有发现将Multi-hOFDM-CPM 联合调制信号应用于C波段卫星导航的公开报道。
Multi-hOFDM-CPM 信号同时具备OFDM 信号频谱利用率高、抗多径衰落能力强以及Multi-hCPM 信号带外辐射低、对邻道干扰小、功率利用率高等优点,且相比Single-hOFDM-CPM 调制,从理论上讲,将Multi-hOFDM-CPM 调制应用于C 波段导航,其基础导航性能指标如兼容性、码跟踪精度、抗多径性能等将获得进一步提高。因此,本文探索将Multi-hOFDM-CPM 联合调制信号应用于C波段卫星导航的可能性。
2 Multi-h OFDM-CPM 信号实现及导航信号初选
2.1 Multi-h CPM调制
CPM的时域表达式为[9]
式中,E为符号能量,T为符号周期,fc为载波频率,φ0为初始相位,α={αi}=(α0,α1,…)为发送的M进制的信息序列,φ(t,α)为t时刻携带信息的载波相位函数。
φ(t,α)第n个符号间隔的表达式为
式中,αi∊{±1,±3,…,± (M-1)},M为进制数;q(t)表示相位脉冲函数;hi={h1,h2,h3,…,hNh}为包含Nh个调制指数的集合,令=imodNh,那么的数值大小以Nh为周期,并且h-i在每个符号间隔中恒定,其周期也为Nh,即hi+Nh=hi。
相位脉冲函数q(t)表达式如下
式中,L为关联长度,g(t)为频率脉冲函数,并且由于g(t)的积分结果q(t)具有连续性,因此这也决定了调制信号相位φ(t,α)的连续性。
2.2 Multi-h OFDM-CPM联合调制
图1 展示了Multi-hOFDM-CPM 联合调制的实现过程。
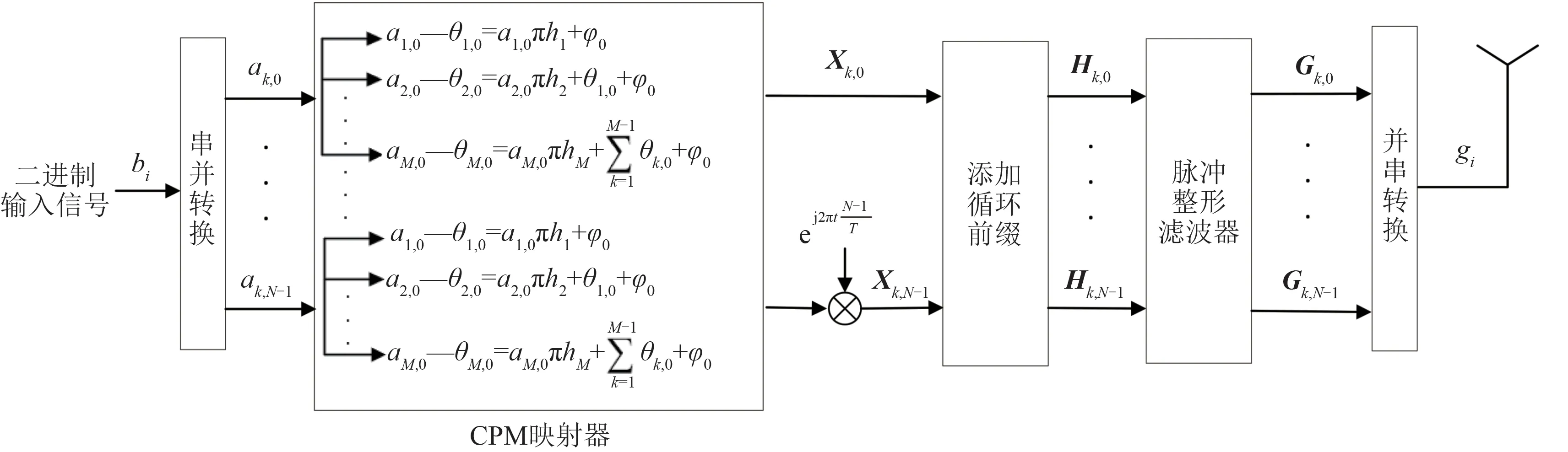
图1 Multi-h OFDM-CPM联合调制的实现Fig.1 Multi-h OFDM-CPM combined modulation system
图1 中,bi(i=0,1,2,…)为调制过程的输入比特序列,其传输速率为1/Tb,通过串并转换,变为单个数据块大小为N、子载波数为N的ak,p,数据块个数(也称“符号数”)为M。
ak,p的定义如下
式中,k=1,2,3,…,M表示第k个OFDM-CPM 数据块,p=0,1,2,…,N-1 表示此数据块中的子载波序号。
ak,p经过CPM 映射器后变换为ck,p,CPM 映射器定义式如下所示
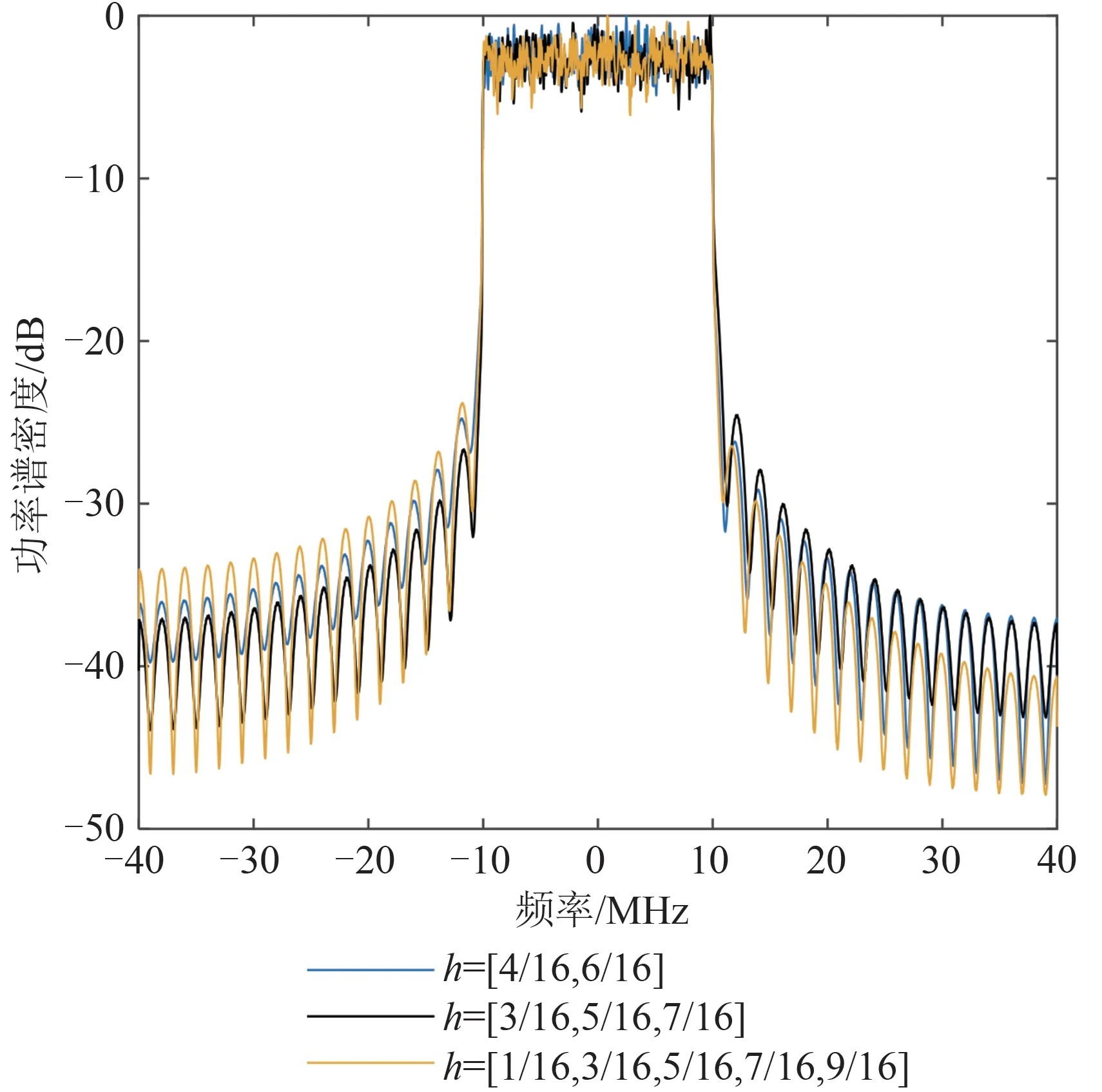
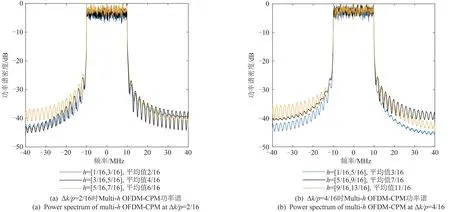
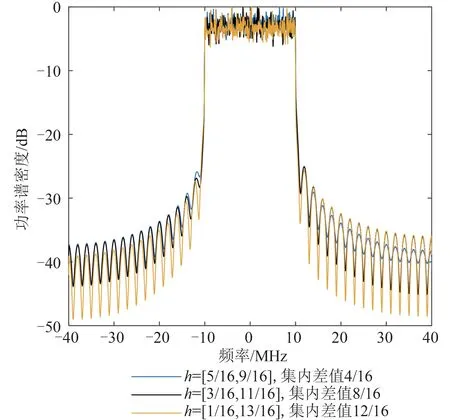
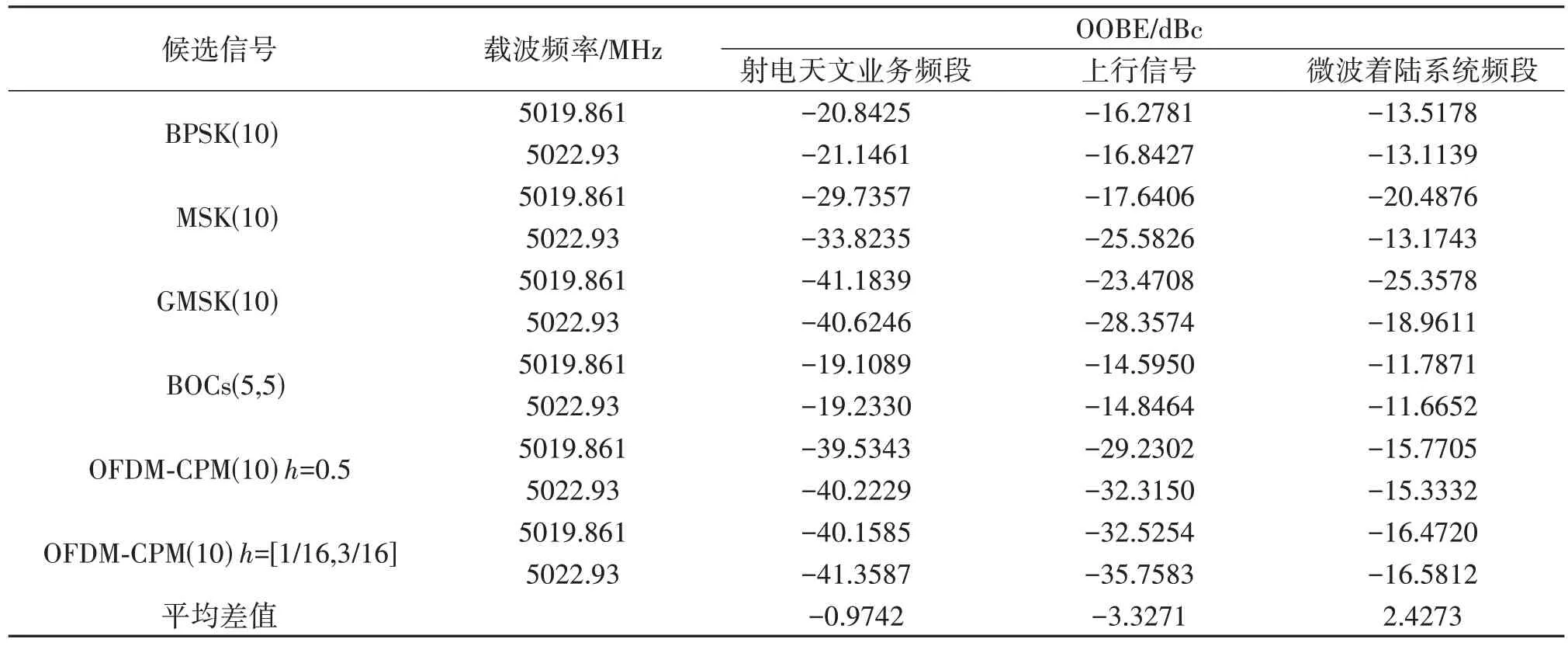
式中,hi为映射器第i个数据块的调制指数,0 通过式(5)及式(6)可以看出,θk,p是由截至运算时的所有信号叠加求和的结果。这使得运算后的相位是连续的、具有记忆性的;并且由于信号幅度不受影响,所有的ck,p均在单位圆上,这些特点均为后续如何准确解调接收信号奠定了基础。 ck,p经过快速傅里叶逆变换后得到Xk,p,表 达式为 为尽可能减小符号间影响,一般在每个OFDMCPM 的数据块之间插入保护间隔,其长度一般要大于无线信道的最大时延扩展,这样一个符号的多径分量就不会对下一个符号造成干扰。但是由于多径传播,会导致不同子载波间相互影响,产生信道间干扰。因此通过在OFDM-CPM 的保护间隔内添加循环前缀信号,使得在进行快速傅里叶变换时,消除多径时延造成的影响。 以Xk,p中第i个数据块Xi,p为例 式中,xi,p为第p个子载波传输的信息。 添加循环前缀如下 式中,d(i)n,m为从第n个子载波xi,p提取的第m个数据,Tg为保护间隔长度。 所有的Ηk,p并行传输,即 Ηk,p进入脉冲整形滤波器,即 式中,L为关联长度,T=NTb是OFDM-CPM 的符号间隔。 若L=1,则该信号形式为全响应,输入信号仅与此刻符号的相位变化相关联;若L>1,则该信号形式为部分响应,输入信号会同时关系到此刻符号和后续L-1 个符号的相位。因此关联长度L与符号数有关,最大值与符号数一致。 鉴于C 波段导航对频谱兼容性要求较高,应优先选择功率谱滚降较快、旁瓣幅度较小的信号。限于篇幅,本文有关Single-hOFDM-CPM 信号的研究成果见参考文献[25],初选出h=0.5、L=64(64 为所设Single-hOFDM-CPM 符号数)的Single-hOFDMCPM信号作为C波段导航候选导航信号。 Multi-hOFDM-CPM 基带信号归一化功率谱密度GMulti-hOFDM-CPM(f)为 式中,N为子载波数,gi为Gk,p进行并串转换后的比特序列,fp为第p个子载波频率。 相比于Single-hOFDM-CPM 信号,Multi-hOFDM-CPM 在调制指数的选取上更具灵活性和多样性。令调制指数的均值为=(h1+h2+…+hNh)/Nh、分子间差值为Δk、关联长度为L、调制指数分母的最小公倍数为p,并且将Δk/p称为指数集内差值,则通过调整Nh、、L和Δk/p,便可得到性能不同的Multi-hOFDM-CPM信号。 图2 展示了调制指数数量Nh对Multi-hOFDMCPM 功率谱特性的影响。当和Δk/p取值相同,Nh由2 增加到3,h分别为[4/16,6/16]和[3/16,5/16,7/16]时,Multi-hOFDM-CPM 信号功率谱曲线不会发生明显变化,几乎可以忽略;但当Nh增大到5,h=[1/16,3/16,5/16,7/16,9/16]时,Multi-hOFDM-CPM 信号功率谱旁瓣振荡剧烈,说明只有适度增加Nh,才能有效增加信号的最小欧氏距离从而改善系统的误码性能,过大的Nh不但会导致Multi-hOFDM-CPM信号频谱宽展、占用带宽更大,还会使系统复杂度成倍增加。一般来说,对于高频谱效率的Multi-hCPM信号而言,Nh=2足矣[18]。 图2 调制指数数量Nh对Multi-h OFDM-CPM功率谱特性的影响Fig.2 Influence of modulation index quantity Nh on powerspectrum characteristics of multi-h OFDM-CPM 图3 调制指数平均值对Multi-h OFDM-CPM功率谱特性的影响Fig.3 Influence of modulation index average on power-spectrum characteristics of multi-h OFDM-CPM 图4 展示了调制指数集内差值Δk/p对Multi-hOFDM-CPM 功率谱特性的影响。当相同、Δk/p逐渐增大时,Multi-hOFDM-CPM 功率谱旁瓣会随之升高。因此,在设计Multi-hOFDM-CPM 信号时,所设Δk/p不宜过大。 图4 调制指数集内差值Δk/p对Multi-h OFDM-CPM功率谱特性的影响Fig.4 Influence of the difference within modulation index set Δk/p on power-spectrum characteristics of multi-h OFDM-CPM 图5 展示了关联长度L与Multi-hOFDM-CPM功率谱特性的相互关系。根据上述分析,调制指数h选定为[1/16,3/16]。当h=[1/16,3/16]时,选取关联长度L分别为1、5、10、64(64 是所设Multi-hOFDMCPM 符号数)的信号功率谱密度进行对比。可以看出,随着L增大,信号功率谱旁瓣越低、振荡越小,当L达到最大值64即与所设Multi-hOFDM-CPM符号数一致时,功率谱滚降最快、旁瓣振荡幅度最小,因此选取L=64作为Multi-hOFDM-CPM信号的关联长度。 图5 关联长度L对Multi-h OFDM-CPM功率谱特性的影响Fig.5 Influence of correlation length L on power-spectrum characteristics of multi-h OFDM-CPM 基于上述关键参数对功率谱特性影响的分析,初选出h=[1/16,3/16]、L=64的Multi-hOFDM-CPM信号作为C波段候选导航信号。 C 波段带宽狭窄,在实际应用中,为充分利用C波段资源,候选信号的码速率均选为10×1.023 MHz。参考Galileo 系统在C 波段选用MSK(10)、GMSK(10)和BOCs(5,5)作为候选,因此本文选取在L=64的情况下、h分别为0.5 和[1/16,3/16]的OFDMCPM(10)信号与BPSK(10)、MSK(10)、GMSK(10)、BOCs(5,5)信号进行导航性能对比分析。目前用来评估GNSS信号的基础导航性能指标主要集中在兼容性、码跟踪精度和抗多径性能等方面。 C波段下行导航信号工作频段为5010~5030 MHz,邻频为RAS 频段(4990~5000 MHz)、C 波段上行信号频段(5000~5010 MHz)以及MLS 频段(5030~5150 MHz),因此在兼容性方面,主要评估C波段导航信号与这三个频段的带外兼容性,评估指标为功率通量密度(Power Flux Density,PFD)和带外发射(Out-of-Band Emission,OOBE)功率。 PFD表达式如下 式中,EIRP为卫星的等效全向辐射功率,Latm为大气衰减,d为地球表面接收机与可见星间的距离,Gs(f)为C 波段信号归一化功率谱密度,Δf分别为RAS频段和MLS频段。 OOBE定义为[26] 式中,Δf分别为RAS 频段、C 波段上行信号频段以及MLS频段。 由于RAS相比于MLS对兼容性的限制更高,因此将Galileo系统中设定的5019.861 MHz合理增大,可有效降低对RAS的影响。通常情况下,生成码率和载频的频率源是相同的,当后者与前者的比值为整数时,导航信号设计的灵活性会得到有效提高。目前GNSS信号的码速率主要为1.023 MHz的1倍、2倍、5倍和10倍,5022.93 MHz不仅与上述码速率成整数倍关系,还比C波段中心频点5020 MHz增加了2.93 MHz。 表1 和表2 分别展示了载波频率分别为5019.861 MHz 和5022.93 MHz 时,C 波段6 个候选信号在不同频段内的OOBE 和PFD 值,设定EIRP为48.8 dBW[27],d为21528 km,Latm为0.5 dB。由表1和表2 的平均差值可以看出,相较5019.861 MHz,载波频率处于5022.93 MHz时能有效缓解对RAS和C波段上行服务信号的干扰,因此将5022.93 MHz选为C波段载频。由表2可知,在RAS频段内,若不借助星载滤波器较强的带外限制,所有候选信号均不能满足PFD低于-196.5 dBW/m2[26]的约束条件。 表1 C波段6个候选信号在不同频段内的OOBE值Tab.1 OOBE values of six candidate signals under frequency bands in C-band 表2 C波段6个候选信号在不同频段内的PFD值Tab.2 PFD values of six candidate signals under different frequency bands in C-band 由于数值较多,为更直观地进行对比分析,表3给出了C 波段6个候选信号在不同频段内OOBE 值和PFD 值的优劣排序,鉴于所有候选信号均能满足MLS 频段内PFD 值小于-124.5 dBW/m2的门限[28]规定,因此表中未涵盖MLS 频段内的PFD 值排序。由表3可以看出,在C 波段6个候选信号中,OFDMCPM(10)h=0.5 信号在RAS 频段的OOBE 和PFD值以及在MLS 频段内的OOBE 值均排在GMSK(10)信号之后;OFDM-CPM(10)h=[1/16,3/16]信号在RAS 频段、C 波段上行信号区间内的OOBE 值以及在RAS频段的PFD值均排在第一位。 表3 C波段6个候选信号在不同频段内的OOBE值和PFD值排序Tab.3 Ranking of OOBE values and PFD values of six candidate signals under different frequency bands in C-band 综上,兼容性由优到劣的排序为OFDM-CPM(10)h=[1/16,3/16]>GMSK(10)>OFDM-CPM(10)h=0.5>MSK(10)>BPSK(10)>BOCs(5,5),且OFDMCPM(10)h=[1/16,3/16]信号改善了OFDM-CPM(10)h=0.5 信号相较于GMSK(10)信号在兼容性方面的略微不足。 民用航空主要使用伪码测距。扩频伪随机码的测距精度通常称为码跟踪精度,直接表征了导航系统的测距性能,评估指标为码跟踪误差和Gabor带宽。 3.2.1 码跟踪误差 相干超前-滞后处理(Coherent Early-Late Processing,CELP)码环鉴相器滤波前、后的码跟踪误差方差即有如下关系 式中,BL为码环噪声单边带宽,Ti为相干积分时间,Br为接收机前端等效低通带宽,Δ 为超前与滞后相关器的间隔,Gs(f)为信号归一化功率谱密度,Gn(f)为噪声功率谱密度,Cs为信号在无穷带宽上的功率。 当仅考虑高斯白噪声干扰时,CELP 码环鉴相器的码跟踪误差标准差为[29] 式中,c为3×108m/s,Cs/N0为载噪比,N0为高斯白噪声功率谱密度。 3.2.2 Gabor带宽 高斯白噪声环境中,CELP 码环的码跟踪误差方差只有在相关间隔Δ 取值极小时才趋于克拉默-拉奥下界(Cramer-Rao Lower Bound,CRLB),并且由于BLTi的权值非常小,可忽略不计,因此当Δ接近0的时候,根据等价无穷小理论,CRLB可近似写为 Gabor带宽定义为 显然在同等码环带宽、积分时间和载噪比前提下,Gabor 带宽反映了GNSS 信号码跟踪精度的极限值,其值越大,码跟踪精度越高。 图6展示了C波段6个候选信号的码跟踪性能。设定参数如下,Ti=1 ms,Δ=0.1 chip,BL=1 Hz,Cs/N0∊[20,50],单位为dB·Hz,图6(a)和图6(b)的Br分别为20 MHz和0~40 MHz。 由图6(a)可知,OFDM-CPM(10)h=[1/16,3/16]信号的码跟踪误差最小,在OFDM-CPM(10)h=0.5信号码跟踪误差已经优于其他调制方式的基础上,再略微增加了一点优势。由图6(b)可知,接收机带宽为20 MHz时,OFDM-CPM(10)h=[1/16,3/16]信号的Gabor 带宽最大,较OFDM-CPM(10)h=0.5 信号具有0.006 MHz的略微优势。 综上,码跟踪性能由优到劣的排序为OFDMCPM(10)h=[1/16,3/16]>OFDM-CPM(10)h=0.5>MSK(10)>BOCs(5,5)>GMSK(10)>BPSK(10),且OFDM-CPM(10)h=0.5 信号已经具备了优越的码跟踪性能,OFDM-CPM(10)h=[1/16,3/16]信号在该基础上又进行了加强。 多径误差包络和平均多径误差是国际上导航信号评估多径抑制性最常用的两项指标。 3.3.1 多径误差包络 多径误差包络是在不同多径延迟下多径效应所引起的最大测距偏差,反映了某一多径延迟所对应的最大多径误差。 假设存在N条多径信号,则CELP 码跟踪环路的多径误差包络为 为简化分析环境,这里只考虑仅存在一条反射信号的情况,即令N=1,则式(20)可写为 3.3.2 平均多径误差 平均多径误差是指将每一路多径信号产生的误差包络求和后取均值的结果,表征了多径时延在特定范围内的总体情况,与多径误差包络之间存在如下关系 式中,εa()表示多径时延在[0,]范围内的平均多径误差,分别表示多径-直达信号相位差为0°和180°、多径时延为时的多径误差。 图7 对比了C 波段6 个候选导航信号的抗多径性能,设定=-6 dB,Δ=0.1 chip,Br=20 MHz。 图7 C波段6个候选信号的抗多径性能Fig.7 Anti-multipath performances of six candidate signals in C-band 从图7(a)多径误差包络图可知,在0~30 m 内,OFDM-CPM(10)h=[1/16,3/16]相应结果最小,略优于OFDM-CPM(10)h=0.5信号。图7(b)展示了6个候选信号平均多径误差与多径时延之间的相互关系,为更加直观地比较抗多径性能的优劣,从坐标上看,OFDMCPM(10)h=[1/16,3/16]信号平均多径误差最大值为2.505 m,相比OFDM-CPM(10)h=0.5、MSK(10)、GMSK(10)、BPSK(10)和BOCs(5,5)信号分别具有0.008 m、0.428 m、0.986 m、1.138 m和1.350 m的优势。 综上,抗多径性能由优到劣的排序为OFDMCPM(10)h=[1/16,3/16]>OFDM-CPM(10)h=0.5>MSK(10)>GMSK(10)>BPSK(10)>BOCs(5,5),且OFDM-CPM(10)h=[1/16,3/16]信号强化了OFDMCPM(10)h=0.5 信号本身优异的抗多径能力,在所有候选信号中表现最为突出。 通过对兼容性、码跟踪精度、抗多径干扰等基础导航性能指标的评估,可以发现OFDM-CPM 调制方式能很好兼顾C 波段的带外约束性和导航性能的要求,较OFDM-CPM(10)h=0.5、BPSK(10)、MSK(10)、GMSK(10)、BOCs(5,5)信号,OFDMCPM(10)h=[1/16,3/16]信号在各项性能上更具优越性,且能改善OFDM-CPM(10)h=0.5 信号在兼容性方面的略微不足。 但总体而言,Multi-hOFDM-CPM 信号虽然相较Single-hOFDM-CPM 信号在导航性能上有所改善,但改善的程度有限。类似地,通过研究发现,将基于PSWF 的Multi-hCPM(Multi-hCPM-PSWF)信号用于C 波段卫星导航,也能得出Multi-hCPMPSWF 相较Single-hCPM-PSWF 信号性能改善有限的结论。由于Multi-hCPM 信号的网格状态数量会随着调制指数数量的增加而呈指数级增长[18],而接收机的计算复杂度与Multi-hCPM 信号的匹配滤波器数量以及网格状态数量基本呈正相关,截至现在,Multi-hCPM 在工程实现上的复杂度依然是限制其进一步发展和应用的关键因素。 因此,在C 波段导航中,只有当接收机采用低复杂度检测算法时,信号处理复杂度被降低,MultihOFDM-CPM 信号才会是比Single-hOFDM-CPM信号更佳的选择。2.3 C波段Multi-h OFDM-CPM信号初选

3 C波段候选信号导航性能评估
3.1 兼容性


3.2 码跟踪性能
3.3 抗多径性能
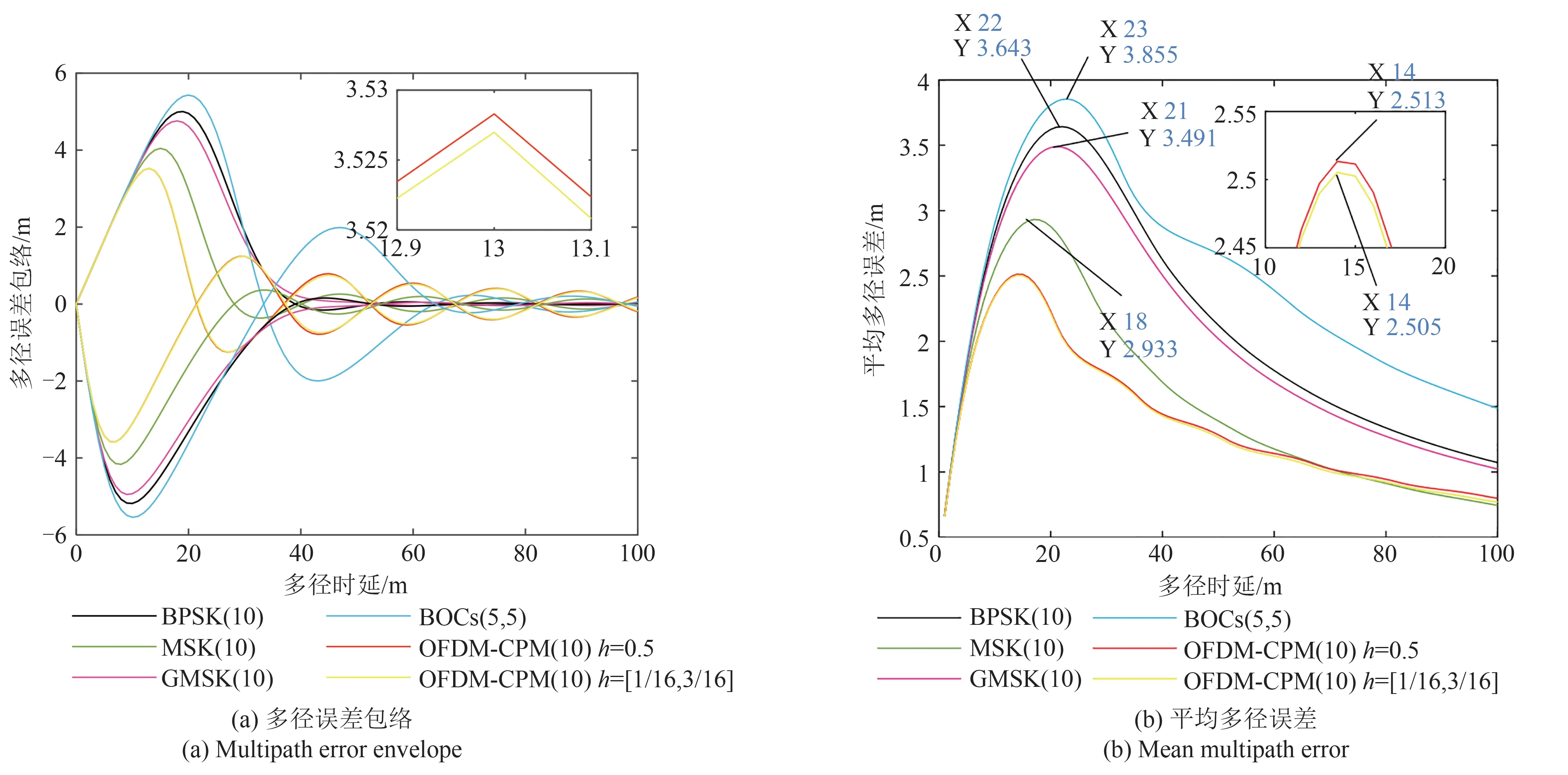
4 结论