带宽化调节下的抗扰PID退饱和控制方法

聂卓赟 聂方明 陈一逢 詹瑜坤罗继亮

(1.华侨大学信息科学与工程学院,福建 厦门 361000;2.厦门市爱维达电子有限公司,福建 厦门 361000;3.鹤壁产业技术研究院,河南 鹤壁 458000)

1 引言

随着“中国制造2025”以及“工业4.0”的不断推进,高端制造业的发展对控制系统提出了更高要求.工业伺服系统在稳定可靠的前提下,追求自动控制的高响应带宽以及抗干扰能力.由于实际系统一般都存在输入限幅约束[1–2],当控制输入超过限幅值时,将产生饱和问题.如果控制量持续处于饱和状态,反馈控制将失去对系统的调节作用,严重时将破坏系统稳定性[3–4].因此工程控制中,必须考虑饱和非线性影响,设计相应的退饱和方案.

针对线性时不变(linear time invariant,LTI)系统,设计理念不同,经典退饱和控制方案可分为3类[5–11].

第1类方案称为“两步法”,即针对LTI系统,首先忽略饱和因素,设计满足控制要求的线性控制器.然后,在线性控制中加入饱和补偿器,降低饱和非线性对闭环系统造成的不利影响[6].这类方法的优点是从设计的角度解耦了系统的线性(非饱和)和非线性(饱和)两种模态,便于工程应用.

第2类方案是同时考虑系统的线性和非线性两种模态,采用非线性系统理论设计闭环控制系统[7].包括基于鲁棒不变集的设计框架[8]与基于定量反馈理论的设计方法[9]等.这类策略的问题在于,两种模态相互依赖且存在耦合,所得到稳定性条件的保守型较强.对不同工业系统,缺乏通用性.

第3类方案是一种低增益设计,即通过降低控制系统的回路增益,以避免控制系统进入饱和状态[10–11].显然,这是一种以降低控制系统性能为代价,被动适应饱和约束的设计方法,不能充分发挥反馈调节能力,误差收敛速度较慢.

在比例–积分–微分(proportional integral derivative,PID)控制中,饱和问题表现得较为明显.由于偏差在积分作用下持续累加,PID 控制量会持续增大,导致控制器输出饱和.这种现象也被称为积分饱和.针对这类情况,Horowitz 和Liao[9]提出了积分抗饱和方法,即当饱和发生时,以反计算的方式通过引入饱和补偿器以调整控制输出,使系统退出饱和状态.基于反计算思想,Herman[10]发展出了条件技术抗饱和方法.结合上述研究,Kothare[6]提出基于饱和补偿器的抗饱和控制统一框架,包括静态补偿方案[13–16]和动态补偿方案[17–20].相对于静态补偿,动态方案往往具有更好的时域性能,但其设计也更为复杂,一直以来也缺乏易用的参数整定方法.在此框架之下,各类PID控制器的抗饱和方法也相继提出.

虽然退饱和补偿的工作机理简单、直观,但现有的退饱和控制设计仍然非常依赖系统的数学模型与各类复杂的稳定性条件[18–20].在工程应用中,人们期望控制性能与控制器/补偿器参数之间能够建立简单、清晰的调节关系,即使系统存在不确定性,仍可基于这种调节关系开展工程应用.自抗扰控制是一类典型的不基于精确数学模型的工程控制方法[21–22],该方法通过对控制器参数的带宽化设计,将抗扰、跟踪性能与控制器参数调节直接地关联起来,在工程应用中表现出较强的鲁棒性和易用性.抗扰PID(disturbance rejection PID,DR-PID)[23–26]是自抗扰控制原理上发展起来的一种带宽化控制方法.本文在DR-PID控制结构中引入退饱和补偿器,研究退饱和补偿的带宽化设计,利用带宽将退饱和性能与跟踪、抗扰性能关联起来,建立简单、易用的PID 退饱和控制方法.首先,结合实例分析PID在饱和约束下引起的不稳定问题;然后,提出退饱和控制的带宽化调节原理,并结合传递函数研究常用一阶或二阶退饱和控制器设计方法;进一步,结合小增益定理[27–28],推导闭环系统稳定下的退饱和带宽与期望闭环带宽之间的约束关系.最终建立一种DR-PID下退饱和控制带宽化设计方法.

2 PID控制中的饱和约束

2.1 抗扰PID

针对图1 所示的二自由度PID 控制系统,文献[23–26]给出了PID控制器的抗扰设计,即

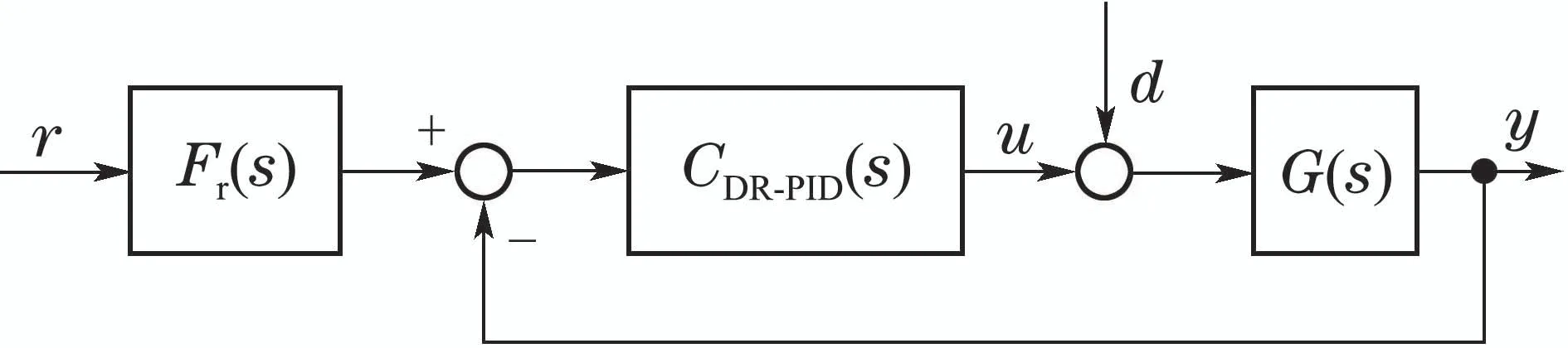
图1 二自由度PID控制系统Fig.1 Two-degrees-of-freedom PID control system

其中:ωc为期望闭环带宽参数,决定闭环响应速度,一般取ωc≈ωb,其中ωb为对象带宽;α代表相位超前补偿因子,若对象响应速度快,则α取小,有0<α<1,若对象响应速度慢,则α可取大,有α>1;Kp>0为控制器增益,逐步增大Kp可改善跟踪与抗扰性能.图1中Fr(s)为前置滤波器,有

其中β≥1.结合主动抗扰原理[24],Kp的调节等效于一类扰动观测器的带宽调节,当Kp足够大时,闭环系统近似为[23,26]

在上述DR-PID参数中,ωc可认为是调节目标,而Kp与α则是实现控制目标的调节手段.PID控制器参数在带宽化[23]设计后,建立了面向控制性能的调节关系,能很好地与工程调参经验兼容.这也是本文在DR-PID下进一步研究退饱和带宽化设计的原因.

2.2 饱和约束下的失稳

从根轨迹的角度来看,饱和特性易使条件稳定系统限制于不稳定状态.考虑文献[5]中的一类不确定系统

其中:a ∈[0.5,0.7],b ∈[0.04,0.1],设计的PID控制器为C(s)=6(1+0.833/s),取Fr(s)=1.图2 给出系统的根轨迹曲线,此时系统处于条件稳定状态.假定饱和约束幅值为±1,当系统进入饱和状态时,系统根轨迹对应的增益系数k ∈[0+,1),在此区间闭环系统可能不稳定.图3给出了r(t)=10×1(t)的响应曲线,此时系统在饱和约束条件下发散.

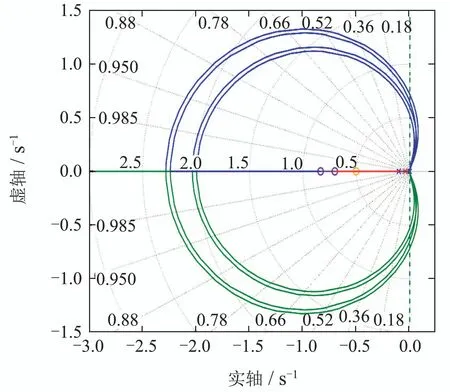
图2 G(s)C(s)根轨迹(不同a,b取值组合)Fig.2 Root locus for G(s)C(s)(with different a,b)

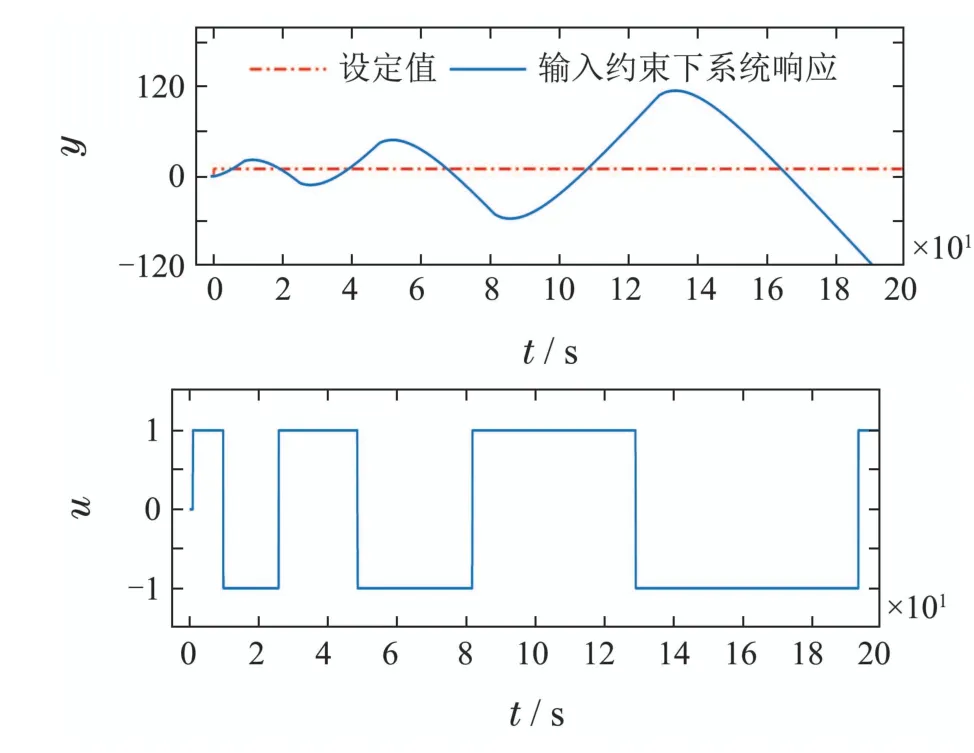
图3 阶跃响应Fig.3 Step response

3 退饱和带宽调节机理

令输入为u∗,则饱和输出u表示为

其中umax和umin分别为执行机构的输入上、下界.在本文分析中,令umax=-umin=1,定义饱和增益ρ=u/u∗∈(0,1],有

本文采用ρ衡量系统饱和程度.

工程中常用饱和环节输出输入的差值构建反馈通道实现饱和补偿,如图4 所示.在“两步法”设计中,C(s)为忽略饱和因素设计的控制器,G0(s)为饱和补偿器.

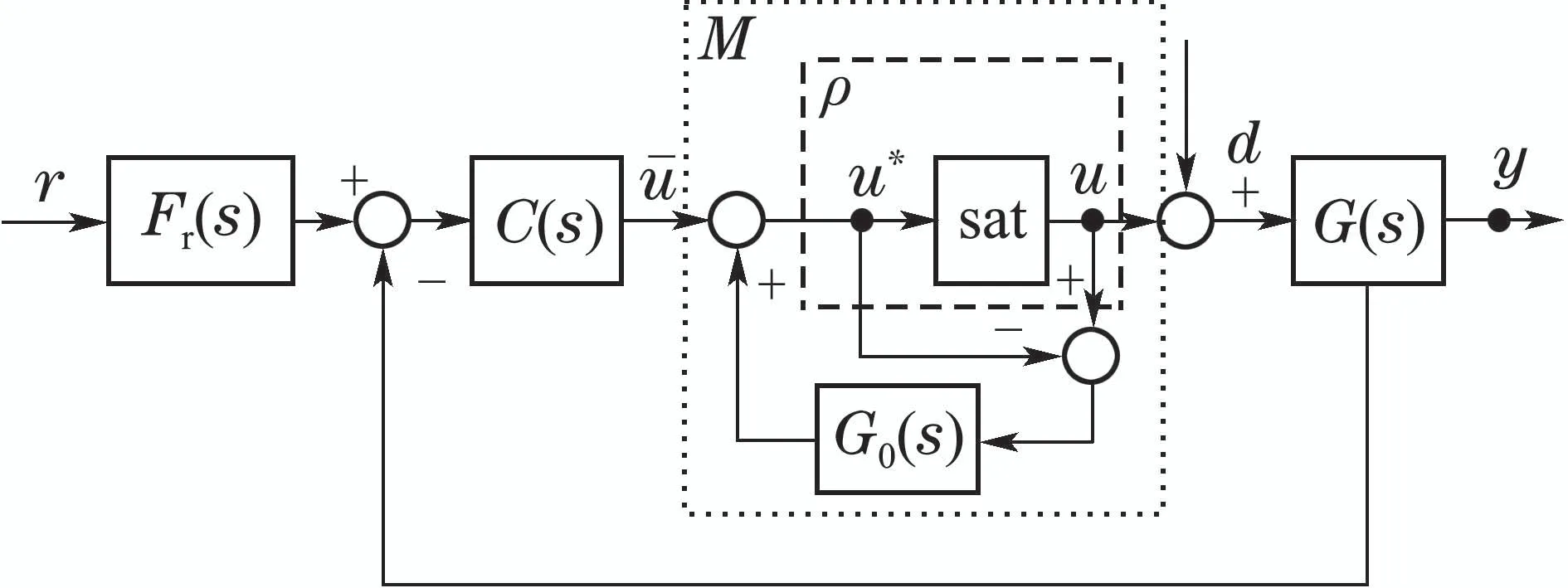
图4 退饱和补偿控制Fig.4 Anti-windup control

对经典积分退饱和补偿,有

其中ωs为增益参数.虽然积分退饱和是一类有效的工程技术,但其工作原理和调参机制仍有待进一步探讨.例如,增益参数ωs的物理含义不明,G0(s)与控制器C(s)之间缺乏清晰的量化关系,特别是对象模型未知的情况下,ωs的调节仅靠试凑调节.

本文考虑一类低阶补偿器G0(s)

讨论退饱和补偿的内在机理,其中:ωs为补偿器增益,τ1>0,τ2>0为时间常数,n为补偿器阶次.

3.1 退饱和补偿机制

在图4 中,ρ的变化一方面取决于退饱和回路G0(s)的反馈机制,另一方面取决于系统动态G(s)、控制器C(s)及各类外部输入.不论外部特性如何演化,退饱和补偿主要依托G0(s)的反馈机制实现.因此,本文针对图5所示的退饱和补偿回路进行分析.

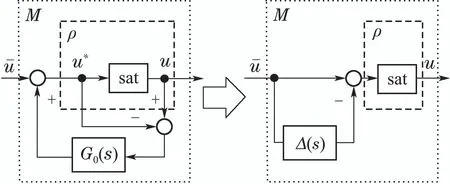
图5 退饱和补偿控制Fig.5 Anti-windup control

对补偿环节进行重构,得到图5所示的等效结构,有

在图5中u(s)=ρu∗(s),u∗(s)=(s)-∆(s)(s),所得等效结构给出退饱和补偿机制:补偿环节M(s)包含了饱和增益ρ与退饱和[1-∆(s)]增益,其中∆(s)为低通滤波器,构成了退饱和通道.当ρ1时,可利用滤波信号∆(s)(s)削弱输入量(s),达到退饱和效果.因此,ωs可视为退饱和通道∆(s)的带宽相关参数,ωs越大其退饱和速度越快.本文将ωs定义为“退饱和带宽”,该参数决定了退饱和速度.

在上述退饱和机理中,∆(s)的动态特性对退饱和性能有着重要影响,包括退饱和速度、振荡等.为此,还可根据期望的退饱和性能直接设计∆(s),以反计算的方式得到G0(s)的实现形式.

3.2 n=1经典积分退饱和分析

n=1即为常规积分退饱和G0(s)=ωs/s,有

对任意ρ ∈[0+,1],ωs>0均满足退饱和带宽条件,此时∆(s)为一阶惯性环节,ωs越大退饱和速度越快.可见,常规的积分退饱和补偿器结构简单、易于实现,具有较好的频率特性,这正是积分退饱和得到广泛应用的原因.

同时,结合上述分析不难发现,当系统进入临界饱和时ρ:1→1-,在小量ωs(1-ρ)→0+情况下,∆(s)主要依靠积分作用来削弱u∗(s).

3.3 n=2退饱和分析

当n=2时,有

为避免退饱和过程的振荡,要求∆(s)的特征多项式包含两个负实根,其条件为

在ωs,τ1,τ2均为正时,如果

则对任意ρ ∈[0+,1],式(10)成立.为应对深度饱和情况,即ρ=0+,可建立一类相对保守的条件,即

满足式(10).

考虑极端情况τ1→0,τ2→∞,当系统处于临界饱和时ρ:1→1-,有ωs(1-ρ)→0+,此时∆(s)近似为双积分,其退饱和速度将快于n=1时的单积分作用.这也是高阶退饱和补偿的主要作用.因此,n=2时一般有τ2>τ1>0.

注1对于G0(s)中n>2的高阶情形,仍可采用本文方法进行分析设计.结合图5给出的带宽化退饱和机制,高阶G0(s)仍将使∆(s)起到滤波和加速退饱和作用.而在饱和参数ρ变化的情况下,高阶∆(s)可能引入振荡.

注2上述退饱和机制与分析是在ρ缓变条件下得到的,而实际情况中ρ的变化可能较快.因此,在补偿器的稳定性分析与参数设计时,需要考虑ρ的一般情况.

4 稳定性分析与设计

本节采用小增益定理[27–28]分析饱和补偿控制系统的稳定性条件,以获得退饱和带宽ωs的稳定区间.同时尝试将ωs和控制带宽ωc联系起来,实现退饱和设计的带宽化调节.

定理1(小增益定理) 考虑如图6所示不确定系统,设M ∈RH∞,令γ >0,则对所有Θ(s)∈RH∞,闭环系统鲁棒稳定的条件为[27–28]:

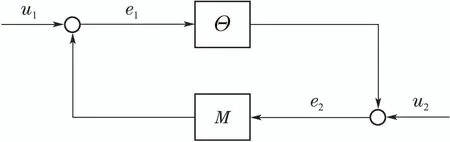
图6 反馈控制结构Fig.6 Feedback control structure

1)∥Θ∥∞≤1/γ当且仅当∥M(s)∥∞<γ;

2) ∥Θ∥∞<1/γ当且仅当∥M(s)∥∞≤γ.

图7是由图4等效变换得到的闭环结构,其中

为饱和函数,且H1∈RH∞.H2为等效传递函数,表达式为

基于小增益定理,可得到如下推论:

推论1考虑如图7所示的控制系统,已知饱和约束环节满足∥H1∥∞=|ρ|≤1,则闭环系统的系统稳定条件为:1)H2∈RH∞;2) ∥H2∥∞<1.

推论2若G(s)包含不稳定极点,则H2(s)必然包含该极点(不发生零极点对消),H2/∈RH∞,稳定条件不满足.

推论1给出了控制器C(s)与退饱和补偿器G0(s)的稳定条件,适用于ρ的一般变化情况.推论2则指出上述方法不适用于不稳定对象.如果对象G(s)稳定且模型已知,有2 种方法设计G0(s): 1) 令G0(s)=G(s)C(s),有H2(s)=0,则推论1成立;2) 给定H2∈RH∞且∥H2∥∞<1,则有

当G(s)未知时,结合DR-PID的主动抗扰机制,闭环控制系统可由(3)式近似表达,其开环传递函数可表示为

因此,不妨直接考虑式(14)所代表的开环系统.在图7中,有

定理2针对系统(14),考虑n=1时退饱和补偿器式(6),如果ωs满足

则由式(12)(15)构建的闭环系统稳定.

证在式(15)中,当n=1,H2(s)∈RH∞为一阶惯性环节

计算得∥H2∥∞=|1-βωc/ωs|.令∥H2∥∞<1,式(16)

成立.根据小增益定理可知,闭环系统稳定.

证毕.

定理3针对系统(14),考虑n=2时退饱和补偿器式(7),如果ωs,τ1,τ2满足

则由式(12)(15)构建的闭环系统稳定.

证当n=2时,

此时,H2(s)的特征多项式即是滤波器δ(s)处于深度饱和(ρ=0+)的特征多项式,而式(11)给出了该特征多项式具有两个负实根的条件.

为便于计算,取ωsτ1=βωcτ2,则有

令∥H2∥∞<1,有βωc/2<ωs.此 时,H2(s)∈RH∞成立.根据小增益定理,如果条件(17)满足,则闭环系统稳定.

证毕.

注3定理2和定理3是针对对象(14)给出的退饱和设计.由于G0(s)的参数设计只与DR-PID的ωc,β参数相关,其中ωs在式(9)中与退饱和通道∆(s)的带宽相关,ωs越大则退饱和速度越快.式(16)–(17)给出了ωs的量化选取依据.

注4饱和发生后,虽然期望系统能快速退饱和,但过大的退饱和作用,也会引起“饱和过补偿”,也可能损害控制性能.例如,当抗饱和能力过强时,伺服系统的带负载能力将减弱,此时需要对ωs进行限制.本文提出的带宽化退饱和控制策略,建立了带宽参数与控制性能之间的明确调节关系,在工程应用中可根据实际系统性能对ωs,ωc等参数进行优化设定.

5 数值仿真

为验证本文所提方法的有效性,考虑不确定系统(4),饱和约束幅值为±1,给定DR-PID,ωc=0.833,Kp=6,α=0,前置滤波器Fr(s)为1.此时闭环系统条件稳定,且存在位于复平面右侧的根轨迹.当系统进入深度饱和时,相当于系统kGC的增益系数k →0+.

由定理2和定理3可知,带饱和补偿器的闭环系统,ωs的约束关系为

引入退饱和补偿后,系统根轨迹稳定性将发生变化.例如,当n=1时,给定饱和补偿环节M(s)=ρs/(s+0.42(1-ρ)).此时,闭环系统在不同饱和程度下的根轨迹如图8所示.当ρ=0 时,即深度饱和情况下闭环系统特征根无限接近于0-,且始终位于复平面左半平面,闭环系统稳定.

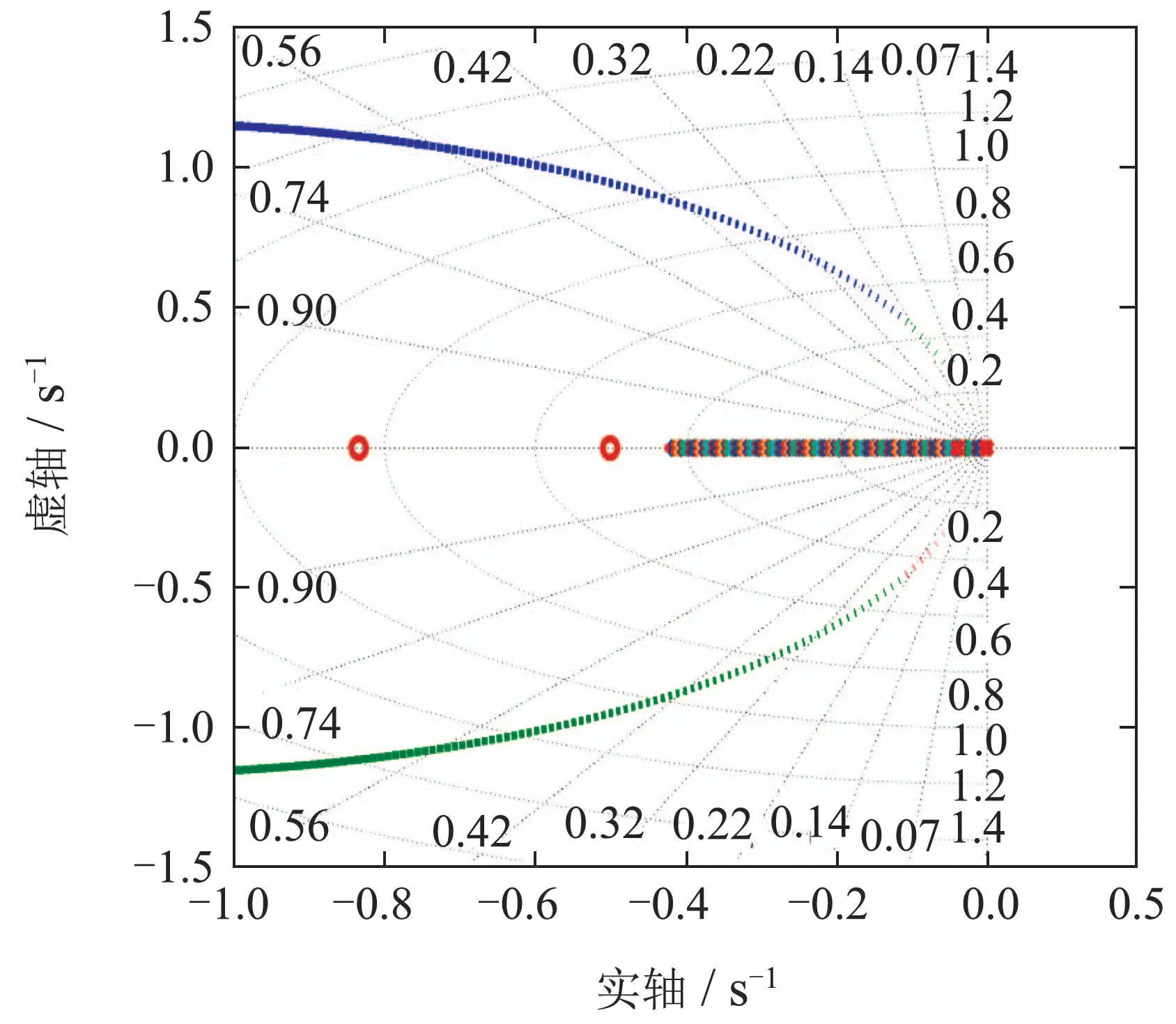
图8 G(s)M(s)C(s)对ρ ∈(0,1]的根轨迹Fig.8 Root locus of G(s)M(s)C(s)for ρ ∈(0,1]

根据参数约束关系,选取

仿真结果如图9所示.可以看出,采用本文提出的参数整定方法,一阶和二阶饱和补偿器都能取得良好的退饱和效果,使原本发散的闭环系统稳定.由于τ2>τ1,二阶退饱和能提供更快的退饱和补偿.

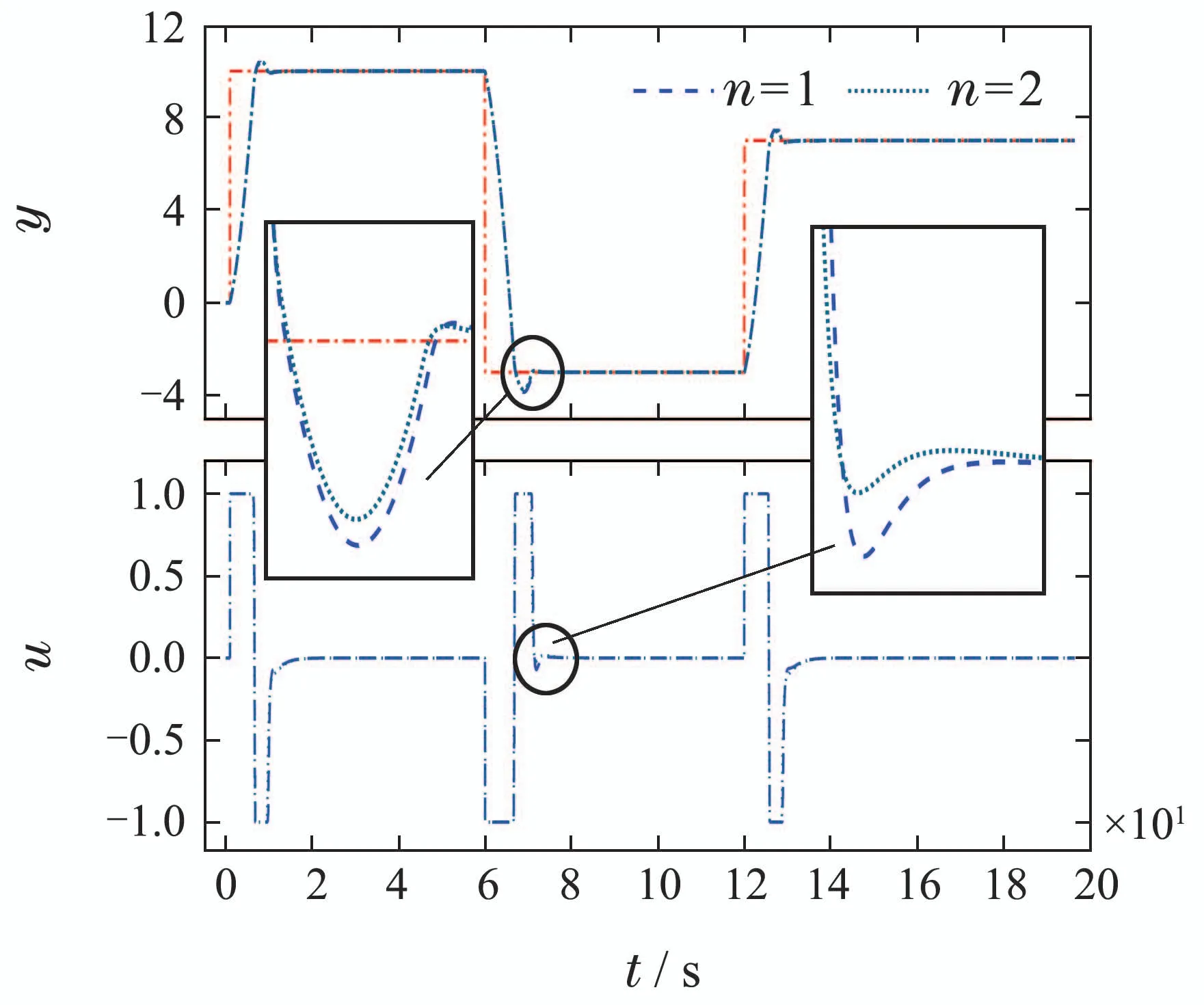
图9 仿真结果1Fig.9 Simulation result 1

针对该对象,文献[5]设计了退饱和补偿器

图10给出本文方法(n=1,ωs=0.42,ωs=2)与文献[5]及一类积分限幅方法比较.可看到,文献[5]提出的方案虽能较快实现退饱和,但退饱和补偿对反馈控制器的负面作用较大,使控制器不能发挥最大性能,系统响应较慢;积分限幅方案(幅值限制为±1)虽能抑制积分累积、避免控制器输出长时间饱和,但仍存在一定的超调,且具体限制幅值的选取依赖实践经验而缺乏理论支撑.

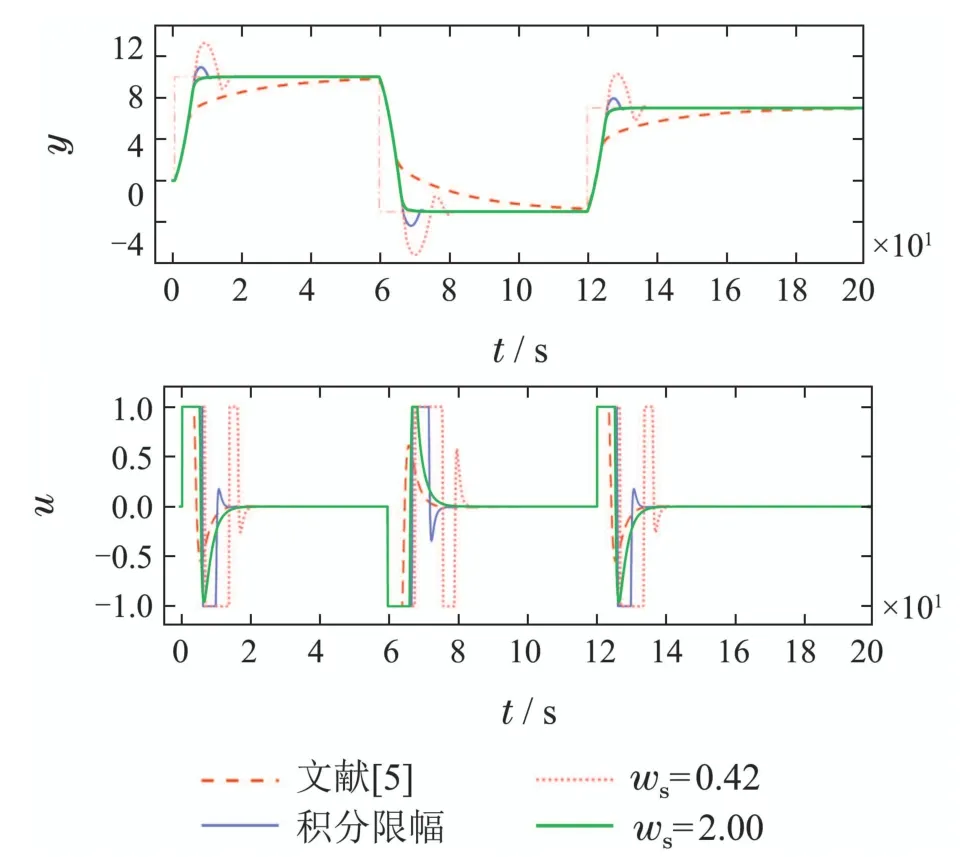
图10 仿真结果2Fig.10 Simulation result 2

在本文方法中,当ωs=0.42时,系统阶跃响应略有振荡、小幅超调,但能保证系统较快进入稳态,此时由于饱和补偿器带宽过小,退饱和速度稍慢;当ωs=2时,系统退饱和速度明显加快,响应曲线无超调.仿真中不难发现,在两个不同的退饱和带宽条件下,闭环系统响应速度几乎完全相同,即由控制带宽ωc=0.833决定.实现了退饱和带宽与控制带宽的独立调节.这正是在DR-PID下退饱和控制带宽化调节的优势所在.

6 结论

本文从工程应用角度出发,考虑PID控制的饱和补偿问题.通过对经典退饱和控制方法的深入研究,首次发现了退饱和补偿的带宽调节机理,同时给出了两类低阶退饱和补偿器的带宽化设计方法.在DR-PID控制结构下,利用小增益定理建立了退饱和控制的稳定性条件.本文提出的带宽化退饱和控制策略,建立了带宽参数与控制性能之间的明确调节关系,在工程应用中可根据实际控制性能对带宽参数进行优化设定.数值仿真结果表明,本文方法能简便、高效地整定PID控制器与退饱和补偿器,达到良好的控制性能.