层间积水对无砟轨道内孔隙水饱和度影响研究
曹世豪,赵锡佳,陈俊旗,王建伟,胡 猛
(1.河南工业大学 土木工程学院,河南 郑州 450001;2.同济大学 道路与交通工程教育部重点实验室,上海 201804)
CRTSⅡ型板式轨道因具有整体性好且维修量少的优点,已被广泛应用于京津城际、京沪、京石武、沪昆及合蚌等线路。截至2021年底,其建设里程将近9 000 km,约占高速铁路总里程的30%[1]。CRTSⅡ型板式轨道作为典型的层状结构(图1),在施工养护不当或者承受极端气候荷载时,极易出现早期层间开裂病害,见图2(a)[2-3]。一旦层间形成积水,将从以下四个方面劣化轨道结构:①高频列车荷载下层间积水内形成的动水压力和高速水流,将加速层间裂缝的发展;②积水的持续浸泡作用将破坏材料表面颗粒与基体间的联结力,形成松散颗粒层;③水作为介质,使有害物富集并将其引入轨道内部;④水侵入结构内部,通过改变孔隙水饱和度而影响混凝土碳化及钢筋腐蚀机制。层间积水的持续侵蚀作用将影响着轨道结构的完整性和承载能力。
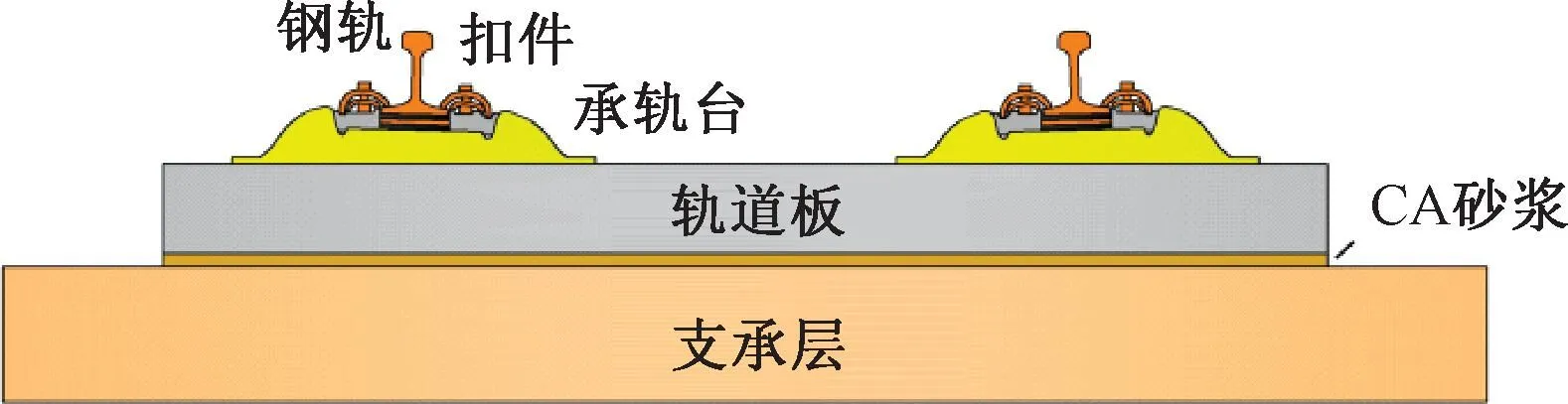
图1 CRTSⅡ型板式轨道结构示意

图2 GRTSⅡ型板式轨道层间病害
由于无砟轨道积水区常伴随着典型的冒泥冒浆病害特征,见图2(b)~图2(d),故应首先从水力劈裂和冲蚀的角度研究了层间水对无砟轨道的影响。Cao等[4]基于流体动力学原理,推导出层间动水压力解析表达式,王明昃等[5]分析了动水压力的时空变化特征。随后基于复合型断裂准则,对无砟轨道层间水力劈裂机理进行分析。Hu等[6]采用Paris疲劳扩展理论,对无砟轨道层间水力劈裂疲劳寿命进行预测。徐桂弘[7]基于多相流理论,分析表面剥离脱落颗粒的冲蚀磨损机理。上述研究成果未考虑水对材料力学性能的影响。
在局部积水环境下,混凝土及砂浆内的自由水将减弱胶凝体颗粒间的范德华力,使得材料力学性能逐渐衰减。混凝土作为常用工程材料,学者们已经对水环境下其力学性能的演变规律开展了大量研究。王海龙等[8]采用断裂力学方法,研究孔隙水压力降低湿态混凝土开裂应力和抗压强度。杨荣山等[9]通过多尺度模型,建立混凝土内部湿度状态与宏观力学性能间的关系。同样地,学者在研究砂浆的浸水软化规律时,采用与混凝土类似的研究方法,对比饱和水下材料的静动态力学性能差异[10-11],并分析水、温度、酸雨、微生物等环境因素的影响[12-13]。随着图像处理技术的发展,工业CT(computed tomography)、低场核磁共振等技术也逐渐被用于砂浆浸水软化机制的细观分析[14]。由于孔隙水自浸水面向内部逐渐衰减的分布特点,会导致浸水表层与内部软化程度存在显著差异。要想准确建立层间积水区表层材料的浸水软化规律,首先需要明确层间积水对无砟轨道内水分分布的影响。
目前,用于衡量多孔材料内水分含量的参量主要有孔隙水饱和度和相对湿度两个。由于直接测量饱和度比较困难,在研究中学者多使用相对湿度描述无砟轨道内水分分布状态。Li等[15]基于Fick扩散定律,分析了无砟轨道早期湿度场分布规律。Cao等[16]采用节点耦合技术,实现了施工过程对早期湿度场的影响研究。刘佳等[17]分析了层间积水对无砟轨道内湿度的影响深度。事实上,无砟轨道内孔隙水含量包含水蒸气和液态水两部分,相对湿度只能反映孔隙内水蒸气的相对含量,而饱和度是表征孔隙水含量更为准确的指标。将饱和度作为变量,来描述CRTSⅡ型板式轨道内水分含量时,将面临三个技术障碍:①无砟轨道内饱和度计算方法未建立;②砂浆材料的饱和度计算参数未测定;③无砟轨道内饱和度瞬态分析时的初始状态不确定。
本文针对CRTSⅡ型板式轨道内饱和度分布特性开展研究,首先采用扫描电子显微镜获取不同尺度下砂浆的孔隙形貌。基于BET多层吸附理论建立干湿环境下的无砟轨道内孔隙水计算方法。开展砂浆毛细吸水试验,测定砂浆的毛细吸水扩散系数,解决了CRTSⅡ型板式轨道内饱和度计算的重要参数问题。采用节点耦合技术,建立层间积水下无砟轨道内饱和度瞬态计算模型。设计的“稳态+瞬态”两步计算流程,解决了非均匀饱和度初始条件问题。最后,分析了环境湿度、层间积水、积水时间等对无砟轨道内饱和度的影响。研究成果可为CRTSⅡ型板式轨道的水致劣化机理及耐久性评估研究提供饱和度理论参考依据。
1 无砟轨道内孔隙结构和水分存在形式
1.1 孔隙结构
混凝土和砂浆等水泥基材料内饱和度与材料的孔隙结构和外部环境水分条件有关。根据孔隙大小和形成原因,可将孔隙分为胶凝孔、毛细孔及气孔三类[18]。以砂浆为例,采用扫描电子显微镜获取不同尺度下的孔隙形态,见图3。

图3 不同尺度下的砂浆孔隙结构
胶凝孔是由水泥水化反应所产生的微小孔隙,其直径一般小于10 nm。毛细孔的主要特征为表面势能明显大于重力势能,并能从空气中吸附水蒸气。当湿度稳定后,小于开尔文直径dk的孔隙将充满液态水,而大于dk的孔隙表面将覆盖一层水膜。开尔文直径dk和水膜厚度ω计算式分别为[19-20]。
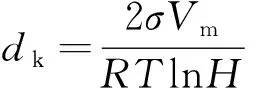
(1)
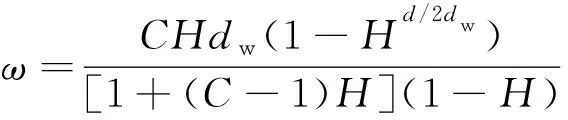
(2)
式中:σ为液体的表面张力;Vm为水的摩尔体积;R为气体常数;T为绝对温度;H为相对湿度;C为BET常数;dw为水分子直径。
大于10μm的孔隙主要是气孔,其中Ⅱ型砂浆的含气量应小于10%。
1.2 孔隙中水分存在形式
根据Feldman-Sereda模型[21],孔隙中的水由自由水、吸附水和化学结合水等构成。自由水存在于大毛细孔(dk

图4 混凝土孔隙中水分与相对湿度的关系
由图4可知,毛细孔隙中的液态水主要形成于H=80%~100%的高湿度环境下。因此,在无砟轨道浇筑完成后的干燥阶段,水会首先脱离毛细孔。
2 无砟轨道水分分布计算原理
直接暴露在大气环境中的无砟轨道,内部孔隙水处于不饱和状态,而影响不饱和孔隙水的环境因素包括干燥和湿润两类:①暴露面干燥大气引起的水分交换;②局部积水引起的毛细吸水。
2.1 干燥环境
在干燥环境下,轨道暴露面与大气间的水分交换为
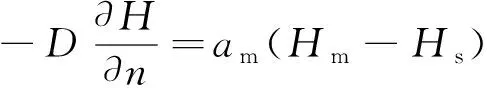
(3)
式中:H为内部相对湿度;Hs为大气相对湿度;Hm为轨道暴露面相对湿度;am为水分交换系数;n为法线方向。
干燥环境下无砟轨道内水分扩散采用基于内部相对湿度的偏微分方程描述[16],即
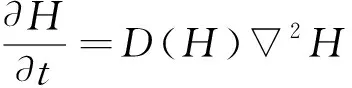
(4)
式中:t为时间;D(H)为以相对湿度H为变量的水分扩散系数;2为拉普拉斯算子。
水分扩散系数D(H)是内部相对湿度的非线性函数,可描述为[22]
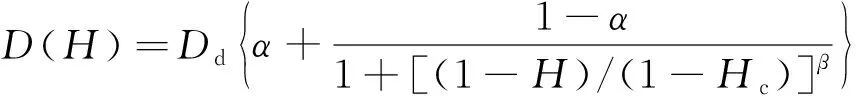
(5)
式中:Dd为最大水分扩散系数;α为最小和最大水分扩散系数之比;Hc为当D(H)=0.5D0时的相对湿度,D0为初始时刻水分扩散系数;β为与材料相关的系数。
2.2 湿润环境
当无砟轨道局部存在积水时,表面水因孔隙的毛细吸水效应而向内部运输,该水分传输过程可采用基于材料内部饱和度的非线性偏微分方程来描述[23],即
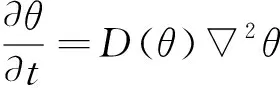
(6)
式中:θ为饱和度;D(θ)为以饱和度θ为变量的水分扩散系数。
毛细吸水扩散系数D(θ)可描述为
D(θ)=Dwexp(iθ)
(7)
式中:Dw为干燥材料的毛细吸水扩散系数;i为常数,一般取i=6~8。
干燥材料的毛细吸水扩散系数Dw与吸水率S、有效孔隙率Φ的关系为[24]
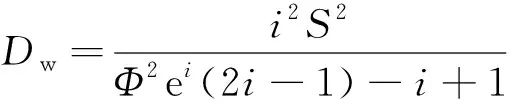
(8)
式中:S为吸水率,可通过材料毛细吸水试验测定;Φ为有效孔隙率,有效孔隙一般是指10~100nm范围的连通孔,常采用的有效孔隙率Φ测试方法包括压汞法(MIP)、恒温恒湿干燥法(CTHD)和核磁共振法(NMR)等。
2.3 干湿环境耦合
Jiang等[25]在BET多层吸附模型的基础上,通过在实验室固定相对湿度环境下测定出饱和度θ与相对湿度H的对应关系为

(9)
式中:λ1、λ2、λ3为与水灰比w/c有关的函数。
3 砂浆吸水试验
为了获取干燥砂浆的毛细吸水扩散系数Dw,设计并开展砂浆吸水试验,见图5。毛细吸水试验装置由砂浆试件、游标卡尺、透明防水胶、恒温干燥试验箱、水盘、电子天平等构成。
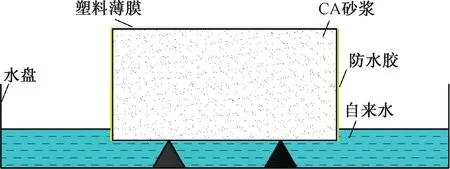
图5 砂浆吸水试验装置示意
砂浆试件采用直径d=100mm、高度h=50mm的饼状试件,配合比为干料∶乳化沥青∶水∶减水剂∶消泡剂=7.9∶1.3∶1∶0.018∶0.000 26。干料和乳化沥青均为济南拓达建材有限公司生产,水为自来水,消泡剂为有机硅消泡剂,减水剂为聚羧酸减水剂,减水率为25%。试件浇筑完成后,将其移入标准养护室内养护,养护条件为:温度为(20±2) ℃、湿度为95%。1 d后脱模,继续在标准养护室养护至7 d,然后移入温度(20±2) ℃、湿度(60±5)%养护室,养护至28 d。试验前,用砂纸打磨掉吸水面自然形成的一层比较致密的沥青膜,采用游标卡尺测量吸水面直径,计算吸水面面积。具体试验步骤如下:
Step1将试件侧面涂抹防水胶,隔绝侧面与外界间的水分交换,形成上下单向吸水。
Step2待防水胶凝固后,将试件移置于60 ℃的干燥试验箱内并定期称重。当两次称重质量差小于0.01 g时停止烘干,并将试件放回试验箱内冷却至室温(约为18 ℃)。
Step3将干燥试件移置水盘中,试件底部吸水面浸入深度为5 mm,保证吸水面完全浸入水中,试件下表面与垫块保持点接触,上表面覆盖防水薄膜。
Step4定时取出试件,用滤纸吸去试件表面的水分并称重,此过程在45 s内完成。
Step5测量试样在48 h内的累计吸水质量m,测量时间间隔为2 h,测试结果见图6。
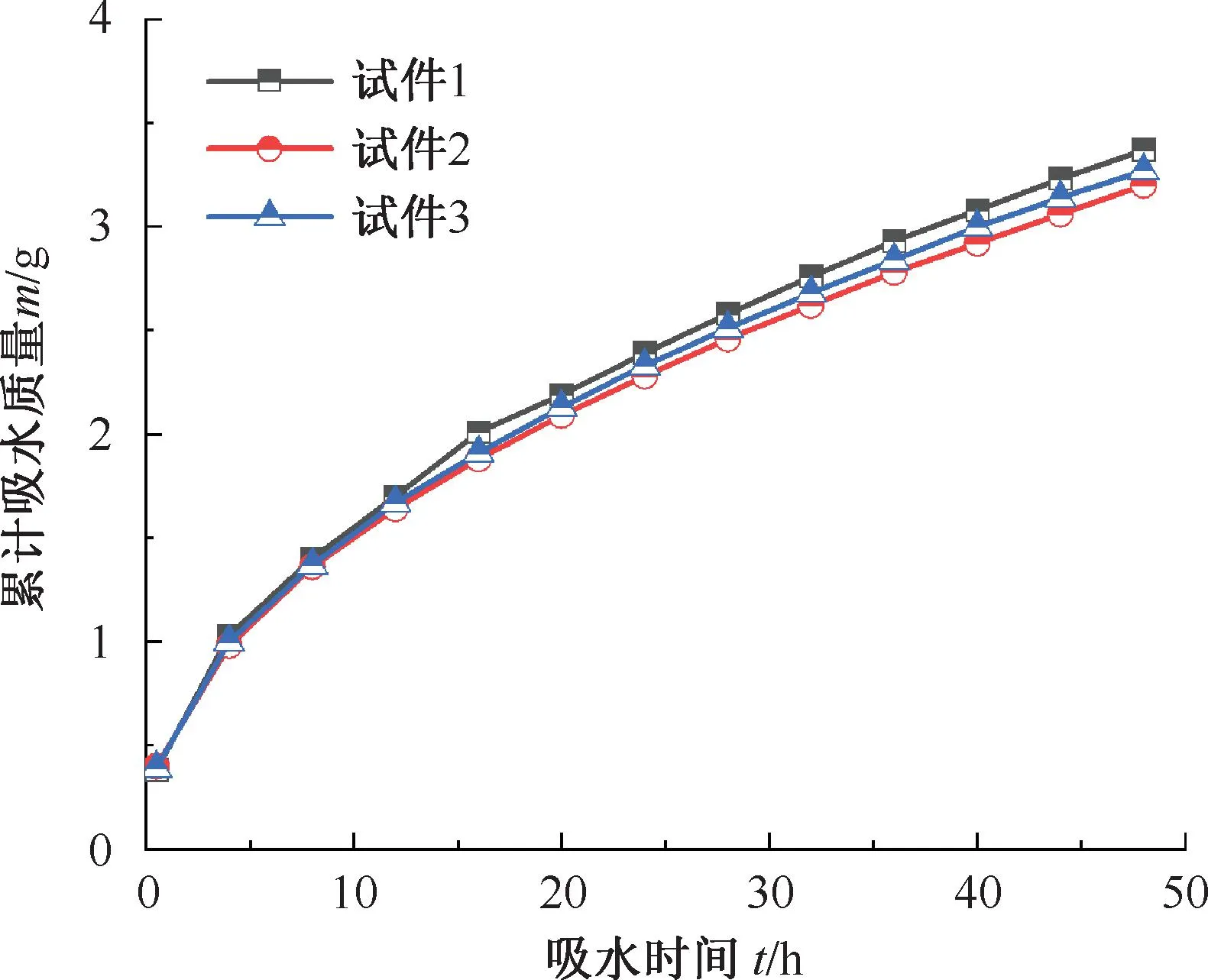
图6 毛细吸水质量与吸水时间的关系
通过对图6所示试验测量m-t曲线进行拟合分析发现,砂浆单位面积毛细吸水量i与吸水时间t的关系为
式中:m为吸水质量;ρ为水的密度;A为吸水面的面积;S为吸水率,通过求平均值,得砂浆的毛细吸水率为S=0.986 8×10-6m/s0.5;t为时间;S0为瞬时吸水量。
此外,采用恒温恒湿干燥法测定的砂浆有效孔隙率为Φ=4.21%。将上述试验测定的吸水率S和有效孔隙率Φ代入式(8)中,计算得干燥砂浆的毛细吸水扩散系数Dw为1.225 5×10-11m2/s。至此,解决了CRTSⅡ型板式轨道层间吸水问题研究的重要参数问题。
4 算例验证
为了验证本文提出的瞬态饱和度计算方法的正确性,选择养护28 d的砂浆试件(未烘干)开展独立性验证试验。试件底面为吸水面,并隔绝侧面、顶面与大气间的水分交换。同时,参考文献[26],建立砂浆试件的饱和度计算模型。计算程序中需将密度ρ与比热容c的乘积设置为1,水分扩散系数D代替热传导系数k。计算模型的初始条件、边界条件与验证试验保持一致。经过48 h吸水,理论计算与试验测试的结果见图7。

图7 理论计算与试验测试结果对比
由图7可知,理论计算的试件湿润区与试验记录的湿润区一致性较好。同时,经过48 h的累计吸水,理论计算的累计吸水量为4.01 g,试验测试的累计吸水量为4.25 g,两者误差小于6%。理论计算与试验测试结果的较为一致性,可认为本文提出的瞬态饱和度计算方法基本正确,且该方法能够有效的评估层间积水下无砟轨道内饱和度的瞬态分布规律。
5 无砟轨道内饱和度计算模型
本文选择路基段CRTSⅡ型板式轨道,分析层间积水对无砟轨道内饱和度的影响,建立的无砟轨道饱和度瞬态计算模型,见图8。计算模型自上而下依次为:预制轨道板200 mm×2 550 mm、砂浆层30 mm×2 550 mm、混凝土支承层300 mm×3 250 mm及路基基床500 mm×4 250 mm。各层结构对应的材料参数见表1[27-28]。划分网格时,砂浆层单元尺寸为5 mm,其余各层单元尺寸为25 mm,生成的有限元模型单元数为6 388个,节点数为20 268个。采用节点耦合技术将砂浆与轨道板、支承层界面黏结为一体,层间界面的开裂通过控制耦合节点对的失效来实现。当层间裂缝内充满水时,与积水直接接触的湿润边界设置为θ=100%的恒定饱和度。基床底部设置为H=90%的恒定相对湿度边界,轨道暴露面施加对流边界,对流水分交换系数为22×10-5m/h,大气湿度值参考北京地区的气象资料,见图9[29]。

表1 材料参数
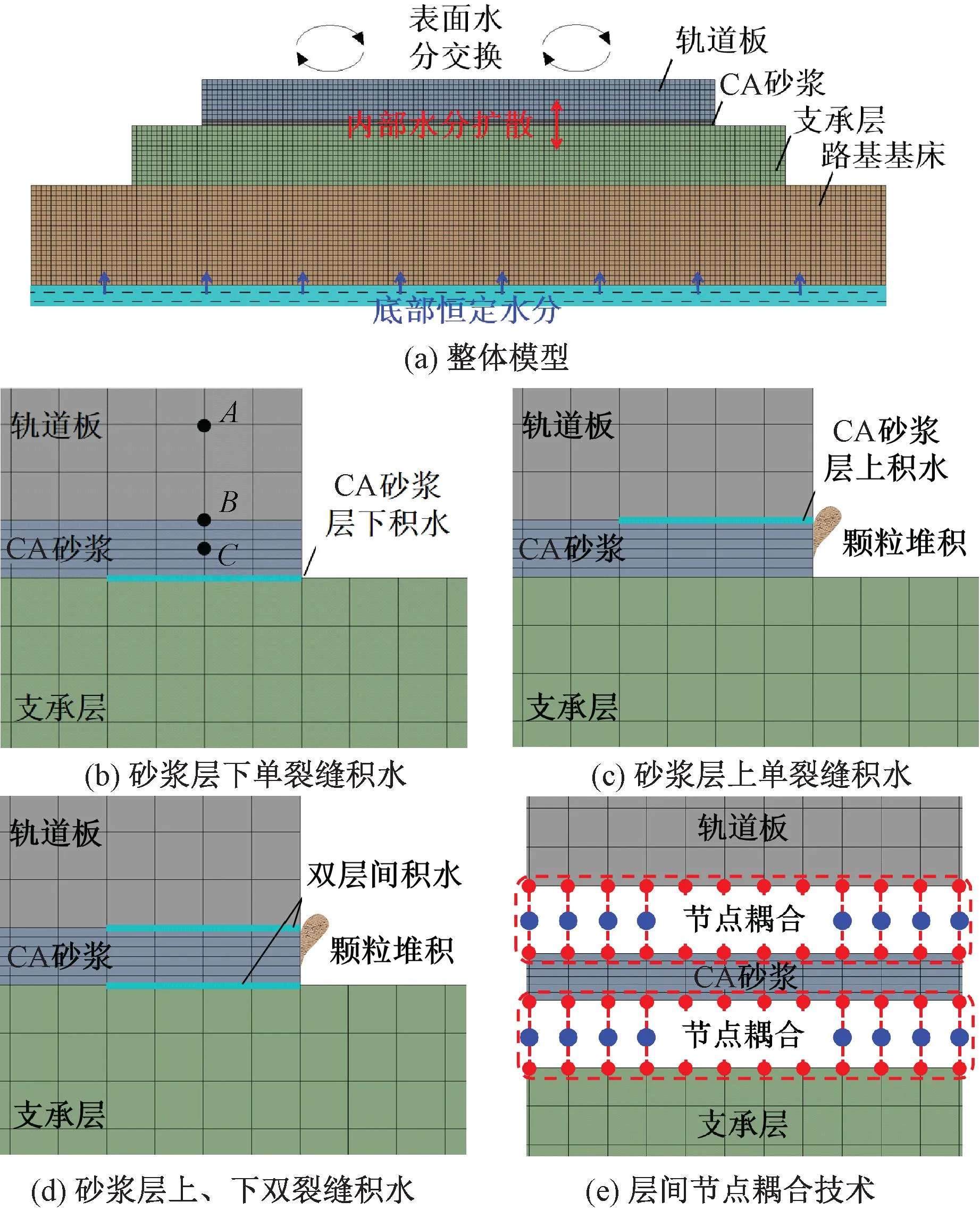
图8 路基上CRTSⅡ型板式轨道饱和度计算模型

图9 北京地区月平均大气湿度
6 计算结果及分析
在分析层间积水对无砟轨道内饱和度影响时,轨道结构内的孔隙水初始状态是不确定的。轨道结构内孔隙水初始状态会受到暴露面大气湿度和基床底部恒定湿度的共同作用,且分布是非均匀的。为了解决该问题,本文设计出“稳态+瞬态”的两步计算方法。首先,通过开展稳态饱和度分析,获得轨道内的平衡饱和度分布规律;然后,将该平衡饱和度分布作为瞬态分析的初始条件,进而实现层间积水下无砟轨道内饱和度分布特性研究。
6.1 稳态饱和度分析
无层间积水时,无砟轨道内的饱和度在暴露面大气湿度和基床底部恒定湿度的长期作用下将处于平衡状态。采用稳态饱和度计算模型分析该平衡饱和度时,参考图9所示北京地区的大气湿度,选择1、4、7、10月四个典型月份,分别代表着冬、春、夏、秋四季。计算的四个典型月份无砟轨道内平衡饱和度分布云图见图10。
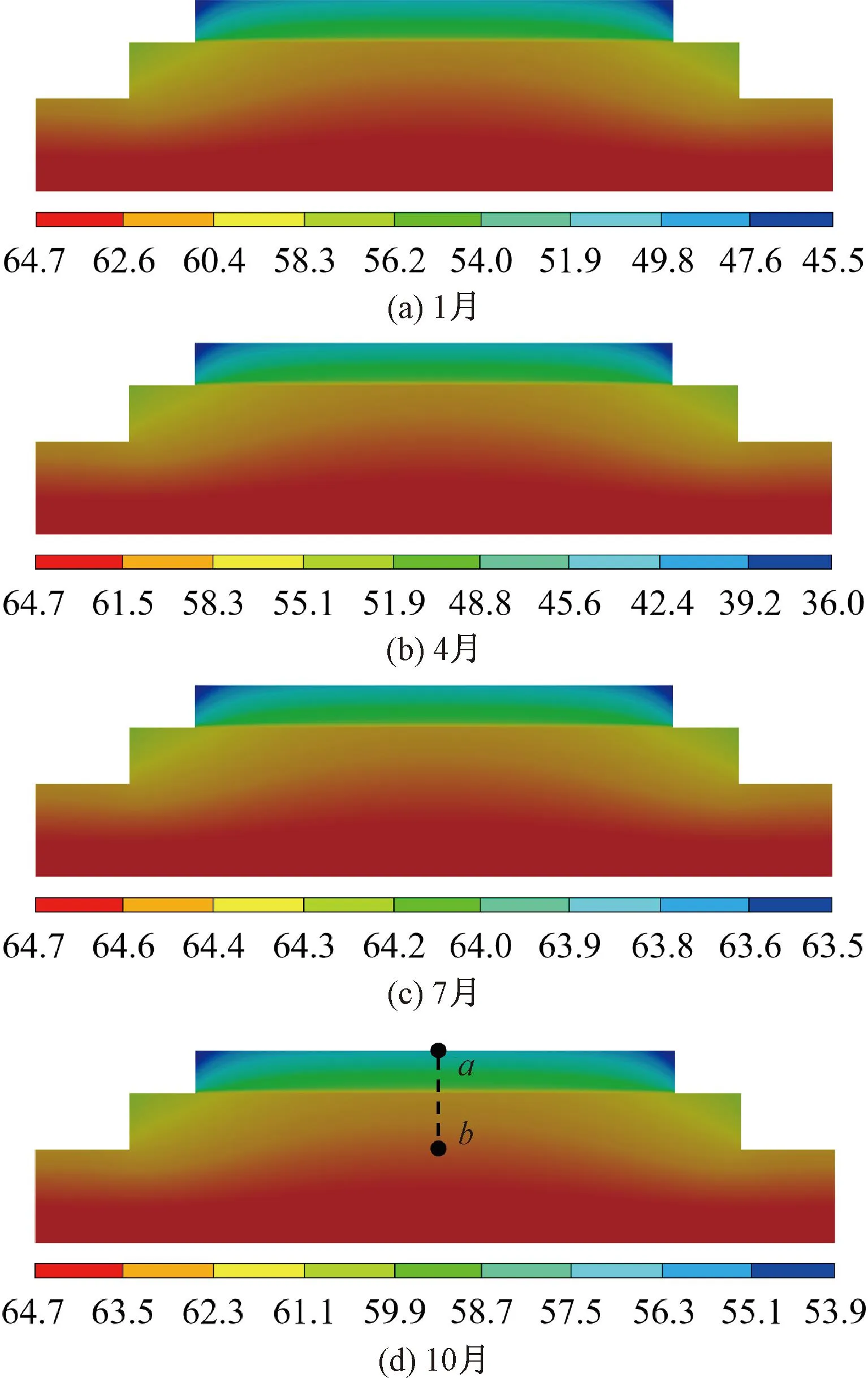
图10 无砟轨道内平衡饱和度分布云图(单位:%)
由图10可知,在基床底部恒定湿度和大气月平均湿度的长期作用下,4个典型月份的无砟轨道内饱和度存在相同的分布规律,其中最低饱和度θ=36%出现在4月份,对应着一年中最干燥的月份。
无砟轨道内平衡饱和度沿着深度方向呈典型的三线性分布规律,见图11(路径ab参见图10(d))。
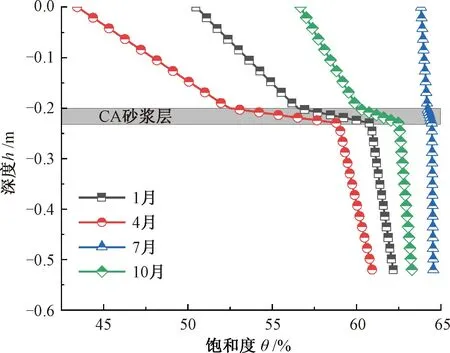
图11 饱和度沿路径ab分布
由图11可知,其中各层内的饱和度梯度由大到小的顺序为:支承层、轨道板、砂浆层,与各层材料的毛细吸水扩散系数大小顺序一致。此外,经进一步分析发现,1、4、7、10月份内砂浆层上下边界的饱和度差分别为4.36%、6.52%、0.27%、2.46%,对应的平均饱和度分别为58.68%、55.67%、64.32%、61.31%。由此可知,砂浆层内饱和度年度差最高为6.52%,其中在夏季(7月)高湿度季节的饱和度基本呈现均匀分布状态。图10所示稳态饱和度分布结果将作为后续层间积水下无砟轨道内饱和度瞬态分析的初始条件。
6.2 砂浆层下单裂缝积水的影响
在雨水丰富或排水系统出现故障时,无砟轨道层间裂缝内会形成局部积水现象。为了分析层间积水对路基段CRTSⅡ型板式轨道内饱和度的影响,假定支承层与砂浆层间存在一0.5 m深的裂缝,且裂缝内充满水,见图8(b)。当裂缝面与水直接接触时,因混凝土、砂浆材料的毛细孔瞬时吸水效应,致使接触面的饱和度瞬间达到100%的饱和状态,见图12(a)。在湿润面的毛细吸水效应下,层间积水将向轨道内持续扩散。通过对比发现,积水向支承层的扩散速率显著大于砂浆层及轨道板,表明低扩散系数的砂浆层对水分的向上运输具有一定的抑制作用,见图12(b)、图12(c)。

图12 无砟轨道内饱和度分布云图(单位:%)
6.2.1 对砂浆层的影响
对于砂浆层,裂缝面饱和度在水浸泡下迅速升至饱和状态,并在饱和度差驱动下向内部扩散,见图13、图14。在浸泡至第2天时,计算点B(B点位置参见图8(b))的饱和度开始增加,表明此时积水已影响整个砂浆层的饱和度分布。随着水分的持续扩散,砂浆层内饱和度将逐渐转变为二次多项式分布。待浸泡7 d后,砂浆层上下边界的饱和度差由49.7%下降至21.7%,且平均饱和度增幅为37.6%。
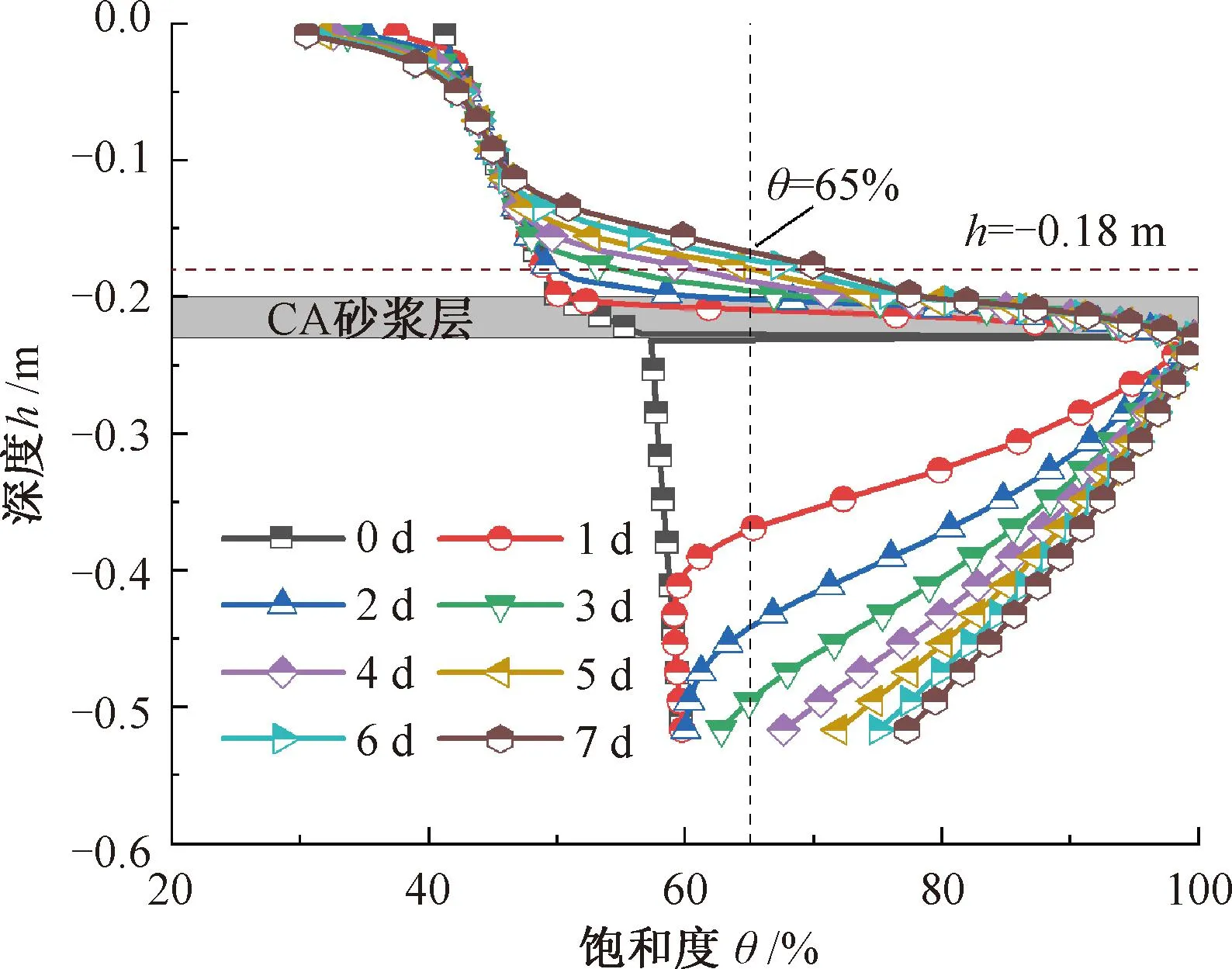
图13 饱和度沿路径cd的分布

图14 砂浆层内饱和度沿厚度分布
6.2.2 对轨道板的影响
由图15中计算点B处的饱和度变化曲线可知,当砂浆层下积水超过1 d后,积水将经砂浆层扩散至轨道板底层,并开始逐渐影响轨道板内的饱和度。在第7天,层间积水对轨道板的影响深度可至100 mm。按照TB 10005—2010《铁路混凝土结构耐久性设计规范》[30]的要求,环境水侵蚀条件下轨道板钢筋混凝土的保护层厚度为20~35 mm。对于预应力钢筋混凝土轨道板,当饱和度较低时,钢筋腐蚀受铁氧化反应为主导的阳极控制,且氧化反应活跃度在饱和度为65%时达到最高;当饱和度大于70%后,铁氧化反应结束,钢筋腐蚀开始进入以析氢反应为主导的阴极控制阶段[31]。基于此,本文选择轨道板底层钢筋处作为饱和度的计算点(参见图8(b)A点,其距轨道板底20 mm)。A点处饱和度时程曲线见图15,以此来评估层间积水对轨道板内钢筋腐蚀机制的影响。由图15可见,A点轨道板内底层钢筋处饱和度从第3天开始增加,并在t=5.4 d时达到氧化反应活跃临界饱和度65%。经7 d毛细吸水作用,A点处的饱和度将达到70%,此后钢筋的铁氧化反应结束,开始进入以析氢反应为主导的阴极控制阶段。
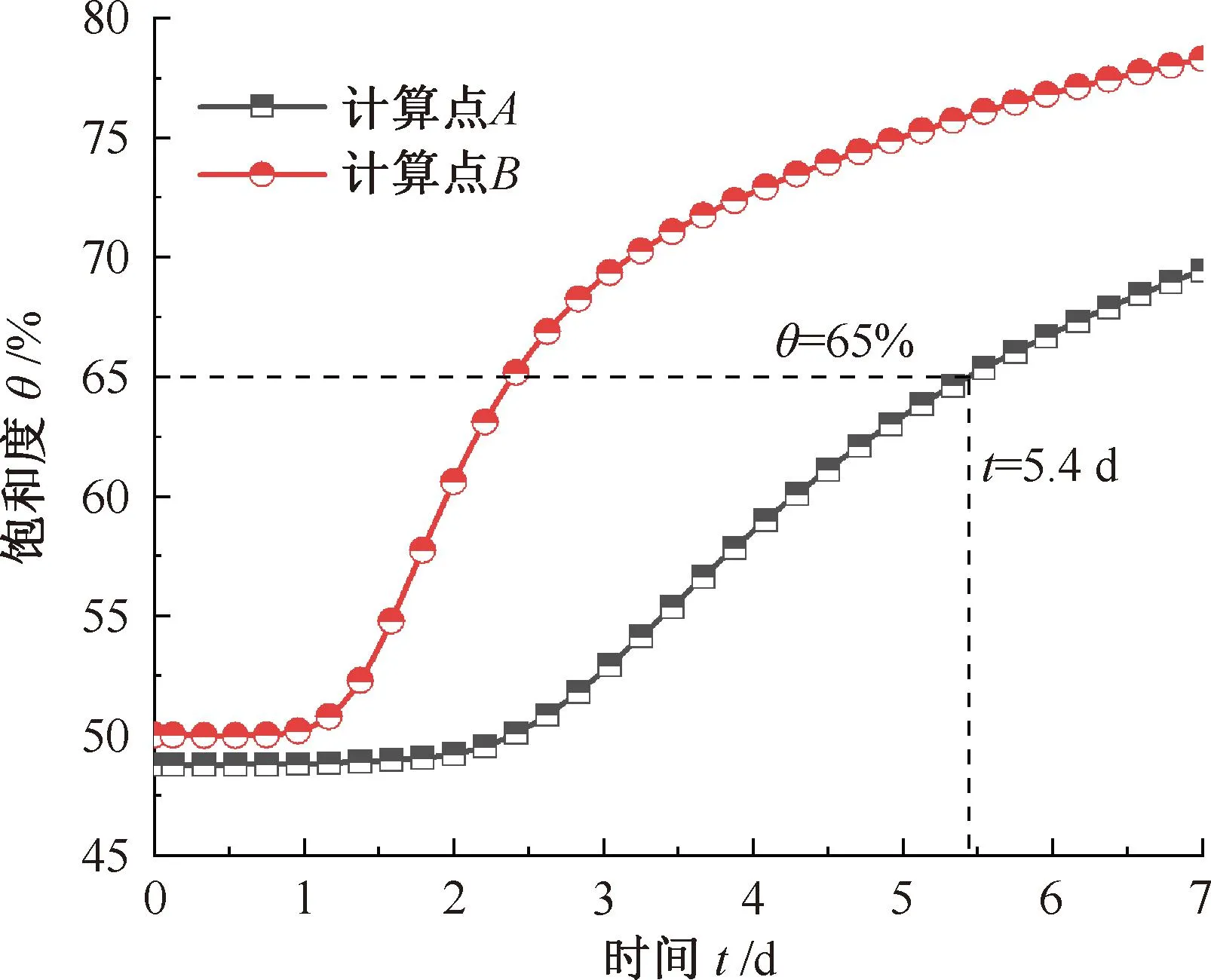
图15 计算点A、B处饱和度时程变化规律
6.2.3 对裂缝前缘的影响
为了分析层间积水对裂缝前缘的影响,计算不同时刻下饱和度沿裂缝前缘的分布规律,结果见图16。图中L=0 m表示裂缝尖端位置,水平轴正向代表着裂缝前缘方向。由此可知,裂缝尖端处积水对裂缝前缘的影响随吸水时间增加而加深。1 d内裂缝尖端处积水可扩散至深度0.14 m处,并在0~0.015 m范围内形成90%以上的高饱和度区。经过7 d的持续吸水,裂缝前缘受影响区发展至深度0.39 m处,而饱和度高于90%的区域达到0.045 m。高饱和度孔隙水的持续侵蚀作用将在裂缝尖端小范围内形成软化区,降低砂浆层与支承层的粘结强度,加速层间裂缝的发展。
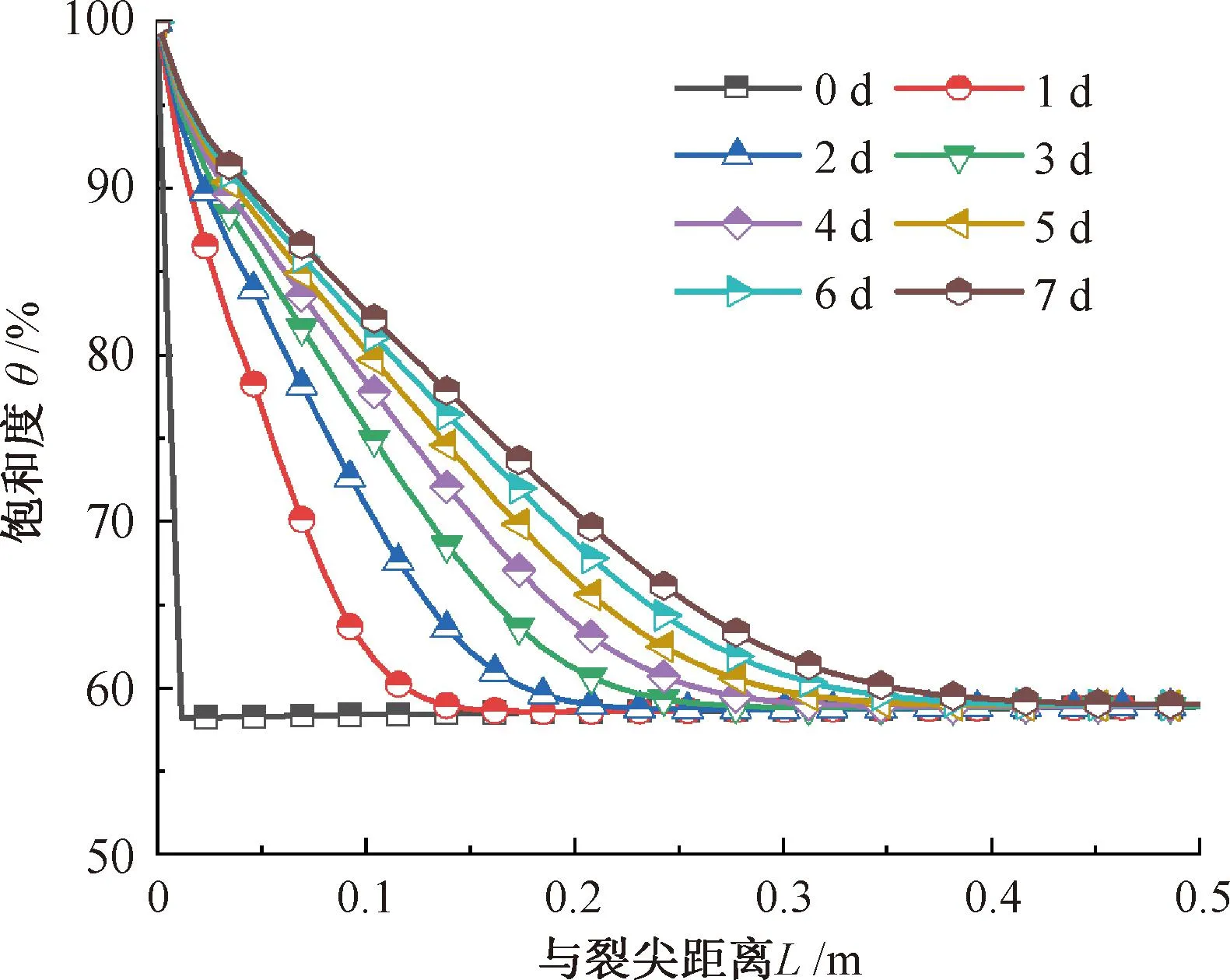
图16 积水对裂缝前缘的影响
6.3 砂浆层上单裂缝积水的影响
当轨道板和砂浆层间存在裂缝时,在雨水天气因裂缝的毛细管吸附力作用,会使得少量液态水进入裂缝内部。随后在列车荷载下形成高速有压水流,反复对裂缝表面进行冲刷作用,破坏表面细微颗粒与基体间的黏结力。裂缝内脱落的细微颗粒随液态水被排除,逐渐在裂缝口形成堆积现象,见图2(d)。当裂缝口颗粒堆积高度大于裂缝开口量时,将会形成砂浆层上裂缝积水现象,见图8(c)。砂浆层上单裂缝积水作用下,计算的轨道内饱和度分布云图,见图17。

图17 无砟轨道内饱和度分布云图(单位:%)
由图17可知,由于低扩散系数砂浆层对水分向下扩散的阻碍作用,使得积水主要向轨道板内扩散。当轨道板底与水直接接触时,接触面的饱和度因毛细孔的瞬时吸水效应而迅速增至100%的饱和状态。经过板底1 d的毛细吸水作用,层间积水可扩散至深度约40 mm处。由图18中计算点A的饱和度时程曲线可知,在吸水初期,轨道板内底层钢筋处饱和度呈现先减小后增加的变化趋势,18 h时达到氧化反应活跃临界饱和度65%,并在36 h后达到90%以上的高饱和度状态,此后轨道板内底层钢筋腐蚀以析氢反应为主导的阴极控制。经7 d毛细吸水作用,层间积水影响深度达到150 mm深,并与暴露面大气湿度影响叠加在一起。此外,通过对比图12和图17可知,砂浆层上单裂缝积水对砂浆层和裂缝前缘的影响与下单裂缝积水的影响基本是一致的,故砂浆层上单裂缝积水对砂浆层和裂缝前缘的影响不再重复讨论分析。

图18 计算点A处饱和度时程变化规律
6.4 砂浆层上下双裂缝积水的影响
通过现场调研发现,在CRTSⅡ型板式轨道层间破损严重区域,会出现砂浆层上、下界面同时开裂的现象。在极端降水条件下,该区段会出现双裂缝同时积水的现象。本节在分析双裂缝积水对轨道内饱和度的影响时,选择图8(d)所示计算模型,模型中支承层与砂浆层、砂浆层与轨道板间裂缝长度为0.5 m,且裂缝内充满水。当裂缝面与水直接接触时,在湿润面毛细吸水效应的作用下,层间积水将同时向支承层、砂浆层和轨道板内持续扩散,影响着轨道内各层构建的水分分布。通过对比三种积水情况下的轨道内饱和度计算结果发现,双裂缝积水对轨道板和裂缝前缘的影响与单裂缝积水的影响基本保持一致,顾双裂缝积水水对轨道板和裂缝前缘的影响不再重复讨论分析。
对于砂浆层,在上下自由水包裹下形成密闭环境,将不再与其他轨道部件进行水分交换,见图19。在湿润面毛细吸水时间超过6 h后,层间裂缝内积水的影响可覆盖整个砂浆层,且平均饱和度增幅为18.76%。在第36小时,整个砂浆层内的孔隙水基本已达到100%的饱和状态,见图20、图21。已有试验测试结果表明,砂浆材料强度在饱和水短期影响下可降低16%,而6轮干湿循环可使折压比下降24.4%,脆性也大为增加[13]。层间积水侵蚀下,砂浆层力学性能的逐渐衰减,将加速砂浆层的破坏,影响着高速铁路的行车安全性与舒适性。
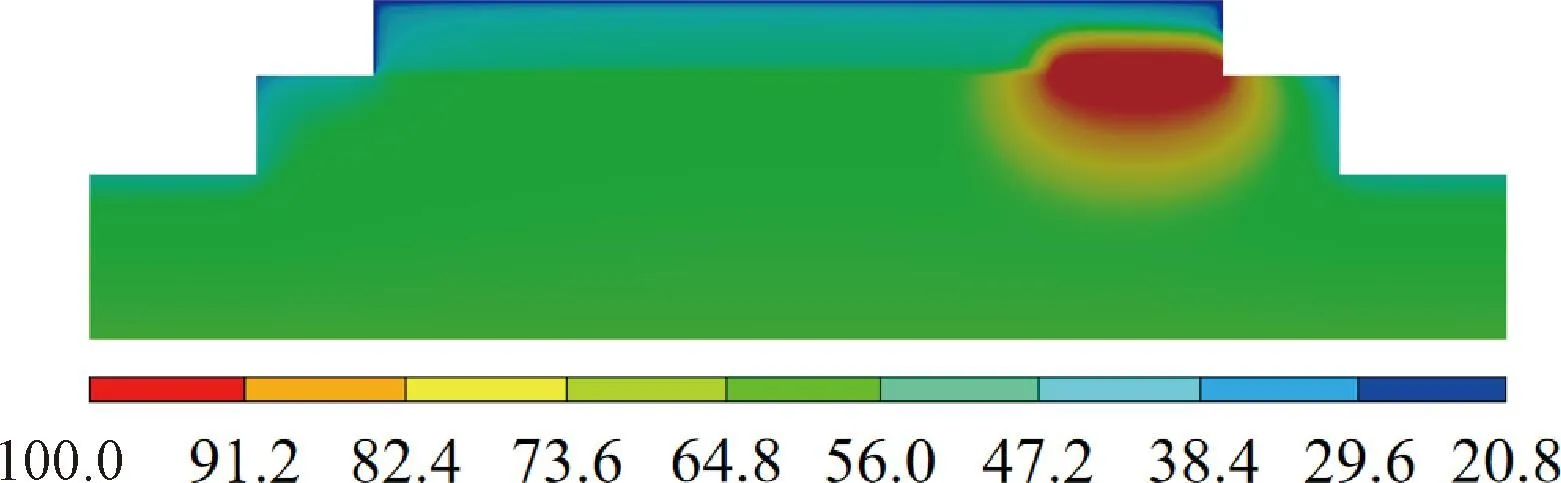
图19 无砟轨道内饱和度(t=7 d)分布云图(单位:%)
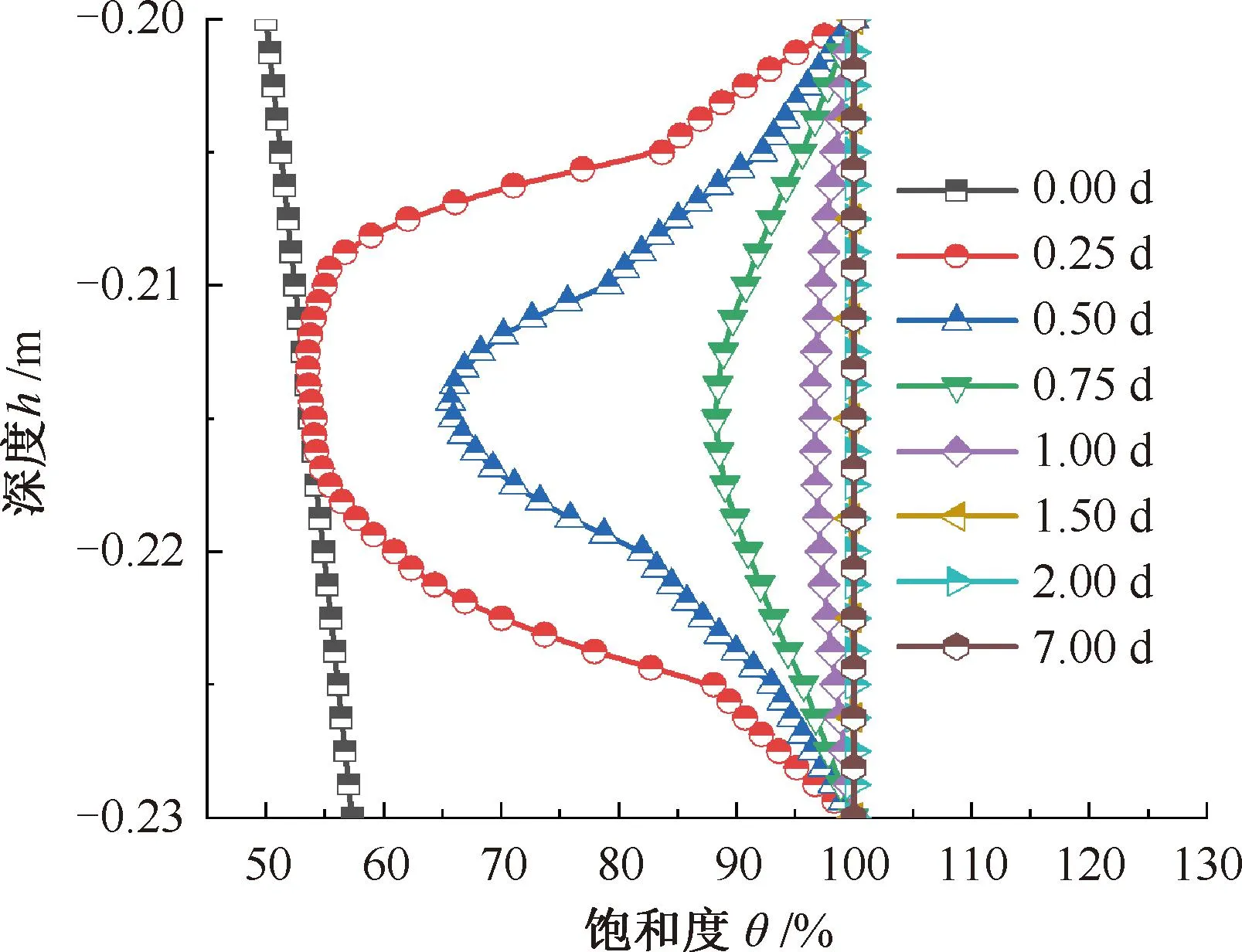
图20 砂浆层内饱和度沿厚度分布

图21 计算点C处饱和度时程变化规律
7 结论
论文针对层间积水对CRTSⅡ型板式轨道内饱和度的影响问题,通过开展试验测试和数值模拟研究,得到以下结论:
1) 开展砂浆吸水试验,测得砂浆的吸水率为0.986 8×10-6m/s0.5,采用恒温恒湿干燥法测定砂浆的有效孔隙率为4.21%,并计算出干燥砂浆的毛细吸水扩散系数为1.225 5×10-11m2/s。
2) CRTSⅡ型板式轨道内形成的平衡饱和度沿深度方向呈三线性分布规律。其中砂浆层内饱和度年度差最高为6.52%,而在夏季(7月)高湿度季节的饱和度基本呈均匀分布状态。
3) 单裂缝积水下,砂浆层内饱和度沿厚度分布将由线性向二次多项式转变。经过7 d的毛细吸水作用,砂浆层平均饱和度增幅为37.6%,轨道板底层钢筋处的饱和度提升至70%,而裂缝前缘的受影响范围约为0.4 m。
4) 双裂缝积水下,整个砂浆层的饱和度在1.5 d时可达到100%的饱和状态。

