基于时频谱图的配电网高阻接地故障智能识别方法

庄文睿, 郭谋发

(1. 福州大学电气工程与自动化学院, 福建 福州 350108;2. 智能配电网装备福建省高校工程研究中心, 福建 福州 350108)

0 引言

为了保持配电网的安全稳定运行, 需对HIF作出可靠的诊断. 当掉落的导线接触到如碎石、 沥青、 树木、 沙砾等表面时, 可能产生电弧, 击穿气隙或接触介质, 并引发HIF[1]. 若不能及时排除HIF, 电弧产生的过电压会造成电力设备损坏、 发生火灾等隐患, 从而威胁财产安全甚至人身安全. 这些风险凸显了HIF识别的重要性.

然而, HIF识别存在如下困难: 由于电弧电阻大, 故障电流小(通常在0～75 A之间), 所以HIF很难被传统的过电流继电器检测到[2]. 除此之外, 受故障发生时接触面材质及配电网拓扑结构不同的影响, HIF所表现出的特征也会有所不同, 噪声也可能造成影响. 故障特征的多样性为HIF识别带来了巨大的挑战.

国内外研究者们已提出多种HIF识别方法. 就特征提取方式来看, 这些方法可以分为3类: 时域分析法、 频域分析法、 时频域分析法. 因为以时间为自变量描述物理量的变化是信号最基本的表达形式, 所以时域分析法具有直观的特点. 其中, 文献[3]根据HIF伏安特性设计检测算法; 文献[4]利用零序电流波形凹凸性在过零点附近的变化来检测HIF; 文献[5]通过零序电流在中性点电流上的投影与中性点电流的差值来判别HIF; 文献[6]使用数学形态学, 从膨胀和腐蚀算子的统计特性中获取特征量, 并将其与阈值对比来完成HIF检测任务. 频域分析法的思路为将信号看作基波及一系列谐波的叠加, 从中分离出需要的分量再加以分析. 其中, 文献[7]分解线电流中的谐波成分, 并以3、 5次谐波的含量和相位作为特征量, 使用模糊逻辑控制来识别HIF; 文献[8]从在变电站处采集的电流信号中提取低次谐波, 训练多层人工神经网络来得到HIF识别结果; 文献[9]基于卡尔曼滤波理论, 通过基波和谐波分量随着时间变化的预测值来检测HIF. 时频域分析法通过设计时间和频率的联合函数, 来同时描述信号在不同时间和频率的能量密度或强度. 其中, 文献[10]使用Stockwell变换来分解电弧信号中的谐波成分, 并利用K-最近邻算法来对不同条件下的电弧信号进行分类; 文献[11]由行波波形的时频域故障信息得到行波全波形, 引入稀疏因子量化时频能谱矩阵的能量分布均匀程度, 构造HIF检测判据; 文献[12]将零序电压进行多分辨率小波分解和信号重构, 根据前后一个工频周期内重构信号的绝对值之和的变化量来判别HIF; 文献[13-16]使用离散小波变换和平稳小波变换来提取HIF的特征, 并训练支持向量机、 人工神经网络、 长短时记忆网络、 随机森林等分类器以区分HIF与非故障事件. 由于HIF的电压、 电流是非平稳信号, 因此, 在3类方法中, 时频分析法能够最充分地利用故障信号中的信息.

在上述方法中, 有不少方法使用了机器学习算法. 这是因为HIF具有随机性的特征, 且现有仿真模型不够精确, 导致基于物理知识和阈值分析的判断方法具有一定局限性; 相比之下, 使用机器学习算法能够有效提高方法的准确率和泛化能力. 即使如此, 在将数据送入分类器前仍需人为构建特征量[17]. 为此, 本研究提出一种新的HIF检测方法, 该方法能提取HIF时频特征并得到其时频谱图, 再使用深度学习算法对其加以识别.

1 配电网高阻接地故障识别方法

1.1 高阻接地故障特征与识别方法

当HIF故障电流即将过零点时, 故障电压瞬时值较低, 电弧间隙电离减弱, 电弧柱直径减小, 导致电弧电阻增大. 在过零点之后, 随着故障电压的增加, 电弧间隙电离增强, 电弧电阻减小[18]. 受电弧电阻非线性的影响, 故障电流也会因此产生畸变. 电弧重燃的过程的随机性使这种畸变也具备随机性. 畸变可能只产生于电流波形的某些周波内, 且在每个周波中的表现也各不相同. 不仅如此, 故障电流还往往出现波动, 且幅值不稳定[19]. 以上种种因素说明HIF故障电流是存在较多变化的非平稳信号, 若使用频域信号处理方式, 则会丢失其在时域中的信息, 反之亦然. 因此, 本文使用时频域信号处理方式来分析HIF波形. 所提方法总览图如图1所示, 首先, 将单相接地故障事件完整波形以每5个周波的长度为一段进行分段, 经由连续小波变换(continue wavelet transform, CWT)得到其时频谱图. 然后, 以半个周波为单位, 将时频谱图切片为方形图像. 将这些图像输入训练好的卷积神经网络(convolutional neural networks, CNN)进行分类, 并依此得到事件的识别结果.

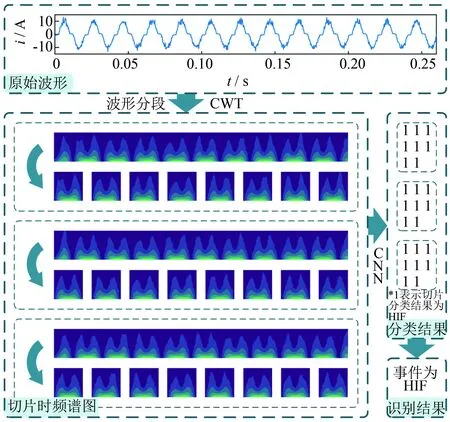
图1 所提方法总览图Fig.1 Overview of the proposed method

1.2 HIF波形的时频分解

在时频域信号处理方式中, 小波变换的基和窗函数是自然收敛的, 因此具有良好的时频局部化特性, 这使其在分析非平稳信号时具有独特的优势[20-21]. 所以, 采用CWT对HIF零序电流进行时频分解.

对于小波基函数ψ(t), 必须满足零均值、 有限能量与容许条件, 即有

(1)

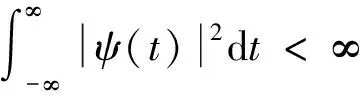
(2)

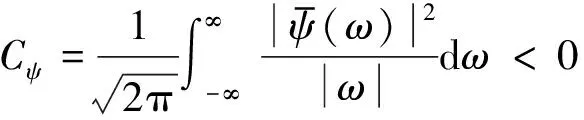
(3)

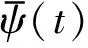
小波变换可以将信号分解为不同的频率分量, 这一过程是通过小波基函数ψ(t)的平移和伸缩实现的. 即

(4)

式中:τ和a分别为平移因子和尺度因子, 两者分别决定了小波的时频窗在时域和频域的位置.

对于任意平方可积函数x(t)∈L2(R)(L2(R)表示能量有限空间), 其连续小波变换C(τ,a)定义为

(5)

使用gaus1小波作为基函数, 50～300 Hz作为特征频段, 对波形作CWT处理. 由于小波变换所得结果不便于直接利用, 为呈现更直观的信息, 以时间为横轴, 频率为纵轴, 颜色深浅代表幅值的绝对值大小, 绘制信号的频率-时间-幅度图, 即小波时频谱图. 连续小波变换时频谱图反映了信号各对应时刻及频率的强度和分布, 能充分反映信号的特征[22]. HIF零序电流原始波形及正弦波波形如图2(a)、 (b)所示, 经变换后得到的时频谱图如图2(c)、 (d)所示. 通过观察两张时频谱图可以发现, 以半周波为周期, 两者都周期性地出现“山”状现象. 不同之处在于, 正弦波形所对应时频谱图中的“山”状呈“峰”形. 而HIF零序电流波形所对应时频谱图中的“山”状呈“齿”形. 所提HIF识别方法基于零序电流时频谱图的这一特征识别HIF. 在使用传统方法时, 电容投切、 负荷投切和低阻接地故障可能被误判为HIF. 除此之外, 考虑到HIF零序电流经CWT变换后得到的时频谱图能够反映零序电流波形中各频率分量的含量, 为确保不会将带有谐波的非HIF波形误判为HIF, 将叠加了随机含量的3、 5、 7次谐波及噪声的正弦波也作为对照. 电容投切、 负荷投切的零序电流及其经CWT变换后得到的时频谱图分别如图2(e)、 (f)、 (g)、 (h)所示. 低阻接地故障的零序电流、 添加谐波与噪声的正弦波及其经CWT变换后得到的时频谱图分别如图2(i)、 (j)、 (k)、 (l)所示. 可见, 只有HIF零序电流波形变换所得的时频谱图具有“齿”形特征, 该特征可以用于区分HIF与典型干扰事件.

在得到零序电流时频谱图后, 使用分类器来判断其是否属于HIF. 传统机器学习算法(如BP神经网络、 支持向量机, 等)大多为浅层算法, 数据分析能力不够强, 精确率受制于特征的表达能力. 如果特征量不能很好地区分信号之间的差异, 学习效果将受到影响[23-25]. 为此, 本研究使用近年来在多个领域取得广泛应用的深度学习技术[26], 增强所提方法的泛化能力, 从而适应不同条件下具有不同特征表现的HIF. 然而, 经过测试, 若将整张时频谱图输入CNN作分类, 则会因为其含有信息过多, 细节过于复杂, 难以取得理想的识别准确率. 为此, 借用目标检测算法的思想, 将单独的“山”状而非完整的时频谱图作为识别的目标. 所提HIF智能识别方法将完整的时频谱图逐个分割为 “山”状图像切片, 分别经CNN得到识别结果, 再依此给出事件的分类结果.

完整的时频谱图逐个分割为 “山”状图像切片的步骤如下.

1) 将原始波形以5周波为单位分段, 两段之间有1周波是重叠的.

2) 将每段波形依次经CWT变换, 以50～300 Hz作为特征频段, 绘制成宽为10h像素, 高为h像素的时频谱图.h取112, 以取得运算速度和精度的平衡; 宽度取为高度的10倍, 使分割后的图像切片为正方形.

3) 对单张时频谱图, 构建数列xn={s+n,s+n+h,s+n+2h, …,s+n+8h}.其中,s=0.5h, 为固定值, 代表为克服边界效应而不采用的时频谱图的边界部分;n∈[0, 0.95h], 为偏移量.取时频谱图最后一行像素, 统计这行像素中位于第k个(k∈x)且颜色为背景色的像素的数量, 记为an.

4) 取能使an最大的n值.若有多个n值满足条件, 则选取其中一个n, 使其他n到该n的平均距离最短.在时频谱图中xn每个元素所对应的位置处设置分割线, 将时频谱图分割为8个切片.

1.3 HIF智能识别方法

1.3.1CNN结构

使用的CNN结构为ResNet101, 其所使用的残差块结构与标准网络结构相比, 不会给网络增加额外的参数和计算量, 但是可以提高训练效果, 并解决随机梯度消失的问题[27]. 完整网络结构如图3所示, 输入尺寸为112×112×3的图像, 一共含有100个卷积层, 用于输入图像的特征提取. 卷积层使用ReLU函数作为激活函数, 卷积核有7×7、 1×1、 3×3等3种大小. 除此之外, 网络中还使用一个3×3的最大池化层和一个步长为2的7×7的平均池化层. 最后, 通过全连接层和softmax函数对图像进行分类.

图3 ResNet101结构Fig.3 Structure of ResNet101

1.3.2HIF智能识别流程

在将一个零序电流波形分段经由CWT得到时频谱图并做切片后, 通过CNN得到这些切片的分类结果. 将HIF标签记为1, 非HIF标签记为0, 并按切片顺序得到8个由1或0构成的序列. 若序列中连续8个数字中存在至少4个1, 则判断该事件为HIF, 否则取下一个零序电流波形分段, 施以相同的处理. 由于每段波形都取自原始波形, 因此须将所得的序列按分段顺序顺次拼接. 重复上述步骤, 直到序列满足被判断为HIF的条件; 或整个波形都经过识别, 却并未满足该条件, 则判断为非HIF. 该识别流程的示意图如图4所示.

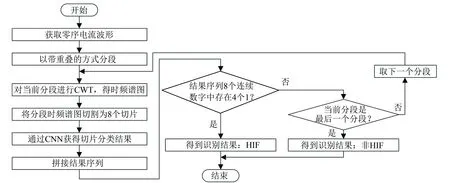
图4 所提方法流程图Fig.4 Flow chart of the proposed method

2 实验验证

2.1 仿真建模

2.1.1HIF模型

使用Emanuel模型[28]模拟HIF, 其电路图如图5所示. 真实的HIF具有不对称性, 即在正负半周波中, 故障电流具有大小不同的幅值. Emanuel模型包含两条并联支路, 每条支路包含一个电阻、 一个电压源和一个二极管, 且两条支路中直流电压源和二极管的方向相反. 当故障点电势高于VP时, 故障电流由馈线流向地. 当故障点电势小于VN时, 故障电流由地流向馈线. 在一个故障周波的前半周波和后半周波, 故障电流分别流经设置了不同参数的两条不对称支路, 以此模拟HIF的不对称性.

图5 Emanuel模型电路图Fig.5 Circuit diagram of Emanuel model

2.1.2配电网模型

利用PSCAD/EMTDC仿真软件建立如图6所示的谐振接地配电网仿真模型, 其工频为50 Hz, 采样率为4 kHz. 图中Us为电源, ZT为Z型变压器, LP为消弧线圈. 该模型具有L1～L7共7条馈线, 馈线类型包含电缆线路、 架空线路、 电缆架空混合线路, 部分馈线含有支路. 各线路长度标注在图6中, 参数如表1所示.

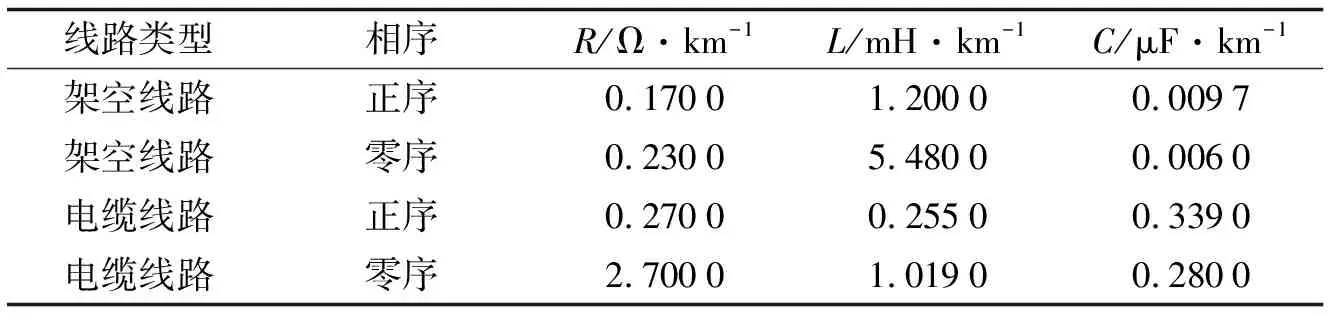
表1 线路参数

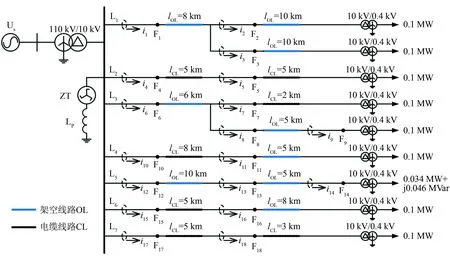
图6 谐振接地配电网仿真模型Fig.6 Resonant grounded distribution network simulation model

在该配电网模型中使用Emanuel模型模拟HIF, 在每次仿真实验中, 设定不同的Emanuel模型参数(不同的VPmax、VPmin、VNmax、VNmin、RPmax、RPmin、RNmax、RNmin), 不同的故障初相角(0°、 30°、 60°、 90°或120°), 不同的故障点(图6中的F1～F18), 不同的网络拓扑结构(初始网络结构, 移除馈线L7后的结构, 或移除馈线L6和L7后的结构), 并采集各馈线上的零序电流.

2.2 对比分析

使用上述模型所得的仿真样本和真实HIF的现场录波样本进行训练和测试.为分析所提方法的性能, 将其与采用时域特征的方法1和采用频域特征的方法2进行对比.

方法1. 文献[29]提出一种基于畸变的HIF识别方法. 将零序电流波形拟合为光滑的曲线, 并构建其区间斜率曲线, 根据曲线中是否出现双“M”形来判断是否发生HIF.

方法2. 文献[30]提出一种基于短时傅里叶变换(STFT)的HIF识别方法. 该方法使用STFT将波形转化为频谱图, 然后使用CNN作为分类器, 区分HIF与非HIF事件.

本研究所提方法与方法1同样关注波形的非线性畸变, 与方法2同样使用CNN识别时频谱图, 但在实现方式上与以上两者皆有本质区别. 为检验识别准确率, 将所提方法与以上两种方法进行比较. 使用与所提方法相同的样本集, 训练方法2所用的CNN, 并对两种方法进行测试, 得到的结果如表2所示. 从测试结果可以看出, 方法1和方法2在仿真样本测试中都拥有很高的准确率, 但在真实样本测试中难以检测出绝大多数的HIF. 这凸显了本文方法所具有的优势.

3 结语

通过对HIF及其他非HIF典型事件进行时频分析, 发现HIF区别于其他典型事件的特征. 为时频谱图设计了一套图像处理流程, 并借助ResNet101作分类. 所提方法最终取得了良好的HIF识别准确率. 从测试结果可得到如下3点主要结论.

1) 以本研究选取的小波基函数和特征频段, 利用CWT对HIF进行时频变换, 所得的时频谱图中所特有的“齿”形特征能够可靠区分HIF与典型干扰事件.

2) 所使用的ResNet101能够有效识别时频谱图切片.

3) 本研究所提方法具有良好的泛化能力, 不仅能够在仿真测试中获得良好准确率, 还能适应现场环境中HIF的随机性.