利用2DGRA-BiLSTM模型的日前光伏功率曲线预测方法
陈柏恒, 陈志聪, 吴丽君, 林培杰, 程树英
(福州大学物理与信息工程学院, 微纳器件与太阳能电池研究所, 福建 福州 350108)
0 引言
太阳能由于其清洁性、 可持续性、 安全性和普遍性, 被认为是未来最有潜力的新能源之一[1]. 然而, 光伏发电高度依赖于气象条件, 天气变化的不确定性严重影响光伏发电的稳定性[2]. 随着光伏发电在电网中的日益普及, 光伏发电固有的不连续性和波动性对电力系统的安全性、 稳定性和经济性构成了巨大挑战. 准确的光伏功率预测可以消除光伏发电设备并网过程中的负面影响.
目前, 现有的光伏功率预测方法主要分为物理法、 统计法、 传统机器学习法和新兴深度学习法. 物理法基于太阳辐照度传递方程、 光伏组件运行方程和其他物理方程, 以实现光伏功率与其他物理参数之间的建模[3]. 但是物理法常常需要大量的输入参数来创建理论公式, 且抗干扰性和鲁棒性较差, 预测精度有限[4]. 统计法通过拟合未来光伏功率, 建立历史数据和目标预测数据之间的映射关系[5]. 常规的统计法包括时间序列模型[6-7]、 模糊逻辑模型[8]、 回归分析模型[9]、 马尔可夫链模型[10-11]等. 而光伏发电仍然是一个动态的、 非周期性的复杂时间序列, 这将削弱统计法通过历史数据对实际功率的拟合能力. 近年来, 大量基于人工神经网络算法的机器学习预测法被提出[12-13], 神经网络技术的发展极大地提高了光伏发电的预测精度. 由于其相对简单的网络结构, 机器学习算法容易出现过拟合和局部最小等问题. 作为机器学习的分支, 深度学习法在准确性、 稳定性和通用性方面取得了巨大进步, 已成为当下光伏功率预测的主流方法[14-17]. 常见的深度学习网络包括全连接神经网络(fully connected neural network, FC)、 卷积神经网络(convolutional neural network, CNN)和循环神经网络(recurrent neural network, RNN). 许多学者通过深度学习法来提高光伏发电功率的预测精度, 文献[16]提出了一种深度CNN模型进行光伏功率点预测和概率预测, 文献[18]应用LSTM-RNN模型预测特定日模式下的光伏功率.
在这些深度学习法中, 与前馈神经网络(FC、 CNN等)相比, RNN不仅可以实现输入层、 隐藏层和输出层之间的信息前馈传输, 还可以实现不同时间输入节点之间的内部状态共享. 因此, RNN在时间序列预测中具有更好的性能. 但RNN仍然存在与前馈神经网络相同的梯度爆炸和梯度消失问题[19-20]. 为了克服这些问题, 文献[21]提出了具有内部存储单元和特殊门结构的长短期记忆(long short-term memory, LSTM)神经网络. LSTM作为一种特殊结构的RNN, 可以有效地记忆和编码长距离时间序列, 并且花费更少的训练时间. 更进一步地, 作为结构改进的LSTM, 双向长短期记忆(bidirectional long short-term memory, BiLSTM)神经网络通过双向连接实现了细胞之间的信息传输. BiLSTM的双向传输结构包括前向层和后向层, 可以同时学习前向和后向时间相关信息. 与LSTM相比, BiLSTM可以学习更多的输入信息, 具有更高的预测精度和更快的学习速度. BiLSTM已应用于许多领域, 如文本聚类[22]、 语音识别[23]等. 但相比LSTM, 现有的光伏功率预测较少能够有效地利用BiLSTM实现预测. 这是由于现有的研究大多是对功率进行点预测, 属于单向时间序列预测. 而BiLSTM的网络特性决定了其在训练和测试时需要同时输入前向和后向时间信息, 点预测无法违背时间规律使用尚未发生的后向信息训练和测试BiLSTM网络. 当一天的光伏功率曲线被视为整体进行预测时, 曲线上的不同时间采样点是被同时预测的, 这使得BiLSTM连接前向和后向的预测信息成为可能.
同时, 短期的光伏发电与短期的天气条件具有关联度, 相同特定天气类型下的光伏功率曲线间相似性往往高于不同天气类型下的相似性. 研究[24-25]表明: 天气分类是提高短期光伏功率预测精度的有效预处理步骤. 特别是对于日前预测, 根据对不同天气分类的预测日建立不同的预测模型对功率预测的精度提升效果更明显[26]. 因此, 本研究根据日功率曲线的波动性将历史数据分为晴空条件、 轻度非晴空条件和重度非晴空条件3种类别.
为预测日前光伏发电日功率曲线, 本研究提出一种二维灰度关联分析-双向长短期记忆神经网络(two-dimensional grey relational analysis and bidirectional long short-term memory network, 2DGRA-BiLSTM)模型. 首先, 2DGRA获取相似日数据, 扩充输入参数. 其次, 基于不同的天气分类条件独立训练BiLSTM模型, 利用其双向传递特性以提高预测精度.
1 功率预测总方案介绍
本研究所提出2DGRA-BiLSTM预测模型的结构如图1所示. 2DGRA基于温度、 湿度和降雨数据获取历史最佳相似日. 所得最佳相似日的功率和斜面漫反射辐照度(radiation diffuse tilted, RDT) 用于扩充原有的气象参数训练BiLSTM网络. 3种天气分类的BiLSTM网络独立训练后进行日功率曲线预测.
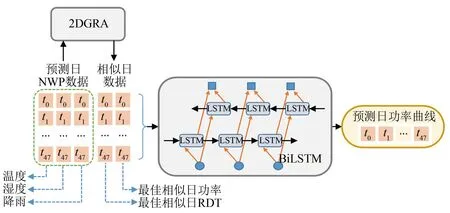
图1 2DGRA-BiLSTM模型流程图Fig.1 Framework of 2DGRA-BiLSTM model
2 算法与网络搭建
2.1 二维灰度关联分析算法
在光伏功率预测中, 灰度关联分析算法(grey relational analysis, GRA)通常用于搜索历史相似日, 以提高功率预测精度[27]. 传统的GRA算法通过计算一维序列之间的关联度来获得相似日数据, 其输入数据维度受限. 当使用多个气象特征作为GRA的输入参数时, 需要对多维输入数据进行重提取或下采样, 以满足一维输入格式的要求. 相比之下, 没有进行特征重提取或下采样的原始气象数据包含更多信息.
为了使用二维数据作为获取相似日的基础, 本研究引入2DGRA算法. 2DGRA算法用于计算比较矩阵和参考矩阵之间的几何相似性. 使用2DGRA计算气象特征矩阵之间的关联度并获得最佳相似日数据的具体步骤如下.
步骤1归一化. 归一化过程为
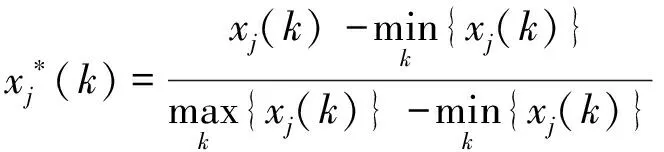
(1)
其中:xj(k) 表示第j个特征中的第k个采样点(j=1, 2, …,m;k=1, 2, …,n).
步骤2构建二维气象矩阵族. 归一化后的历史气象数据按天(24 h)重组成L个m行n列矩阵(A1,A2, …,AL).即
其中: 矩阵族中每个矩阵Ai(i=1, 2, …,L)代表总体气象数据中一天包含的数据分量.每个矩阵每行(j=1, 2, …,m)对应不同天同一时刻的气象特征采样点, 每个矩阵每列(k=1, 2, …,n)对应气象特征数.
步骤3确立参考矩阵和比较矩阵.初始化令p=1, 将矩阵族中第p个矩阵Ap设为参考矩阵, 除第p个矩阵外的其他矩阵设为比较矩阵族(Ai, i≠p).令y(j,k)为参考矩阵Ap中第j行k列的值,xi(j,k)为比较矩阵族(Ai, i≠p)中第i个比较矩阵j行k列的值.
步骤4计算关联系数.依次计算y(j,k)和xi(j,k)的关联系数, 即
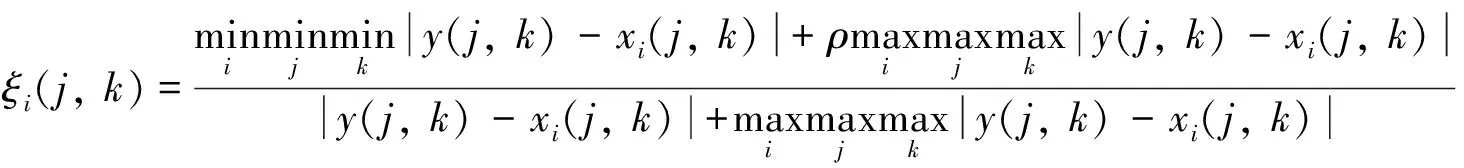
(2)
其中:ρ为分辨率系数, 且ρ=0.5.
步骤5计算关联度. 在已知关联系数的基础上, 依次计算参考矩阵和比较矩阵族的关联度. 即
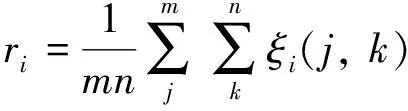
(3)
步骤6确定第p个矩阵对应最佳相似日.将步骤5中计算关联度从大到小排列, 最大关联度所对应比较矩阵即为第p个参考矩阵对应最佳相似日.
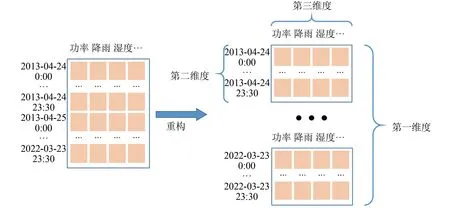
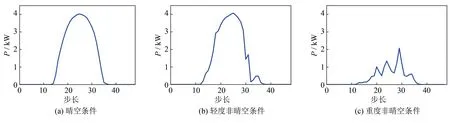
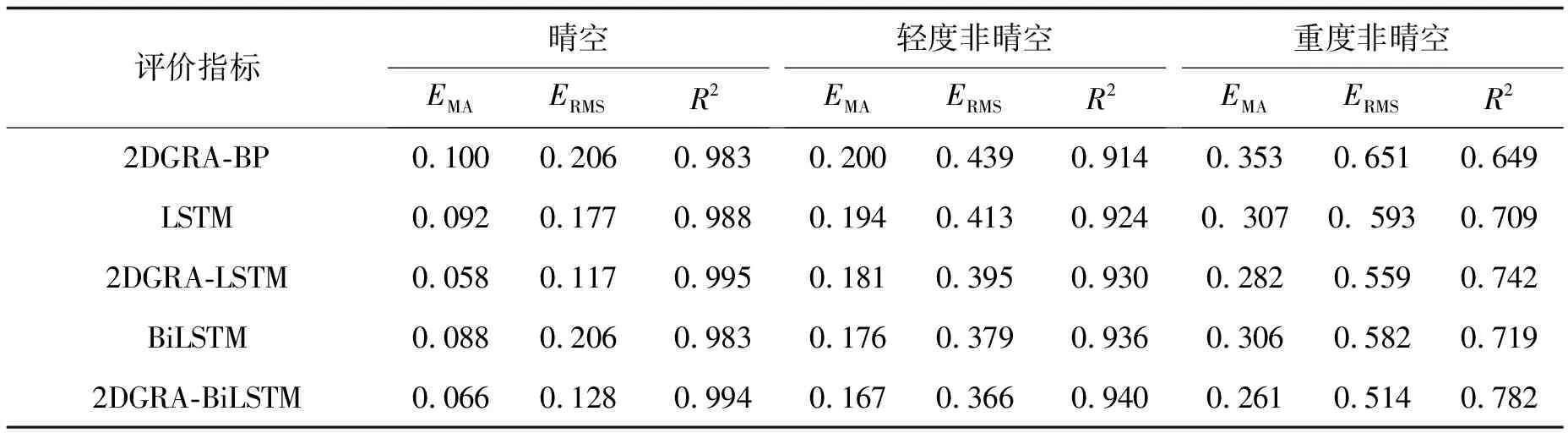
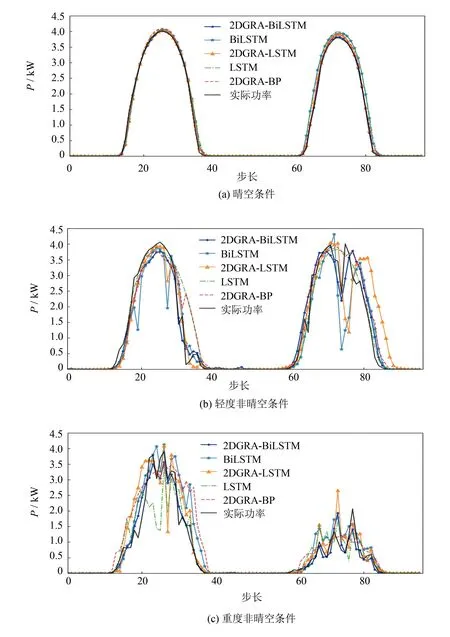
步骤7参考矩阵遍历矩阵族.当p 每个LSTM细胞都具有3个特殊的门结构: 遗忘门、 输入门和输出门(图2). 对应核心计算式[28]为 ft=σ(Wf[ht-1,xt]+bf) (4) 图2 LSTM细胞结构Fig.2 Structure of single LSTM cell it=σ(Wi[ht-1,xt]+bi) (5) gt=tanh(Wg[ht-1,xt]+bg) (6) ot=σ(Wo[ht-1,xt]+bo) (7) ct=ftct-1+itgt (8) ht=ottanh(ct) (9) 其中:σ为sigmoid函数;Wf, i, g, o和bf, i, g, o分别对应权重矩阵和偏移向量. 每个LSTM细胞通过3个门结构对t-1时刻细胞状态ct-1和隐藏状态ht-1进行更新. 将多个LSTM细胞通过单向时间线连接起来即构成了LSTM网络, 如图3所示. 每个时刻LSTM单元隐藏状态ht的sigmoid函数即为当前时刻LSTM网络的输出yt, 即 图3 LSTM网络结构Fig.3 Network structure of LSTM yt=σ(ht) (10) LSTM网络通过单向连接实现细胞间的信息传输. 进一步地, BiLSTM网络通过双向连接实现细胞间的信息传输. BiLSTM在网络结构上比LSTM多了一层后向传输隐藏层, 如图4所示. 相应地, BiLSTM网络的输出计算[29]进一步扩展为 (11) (12) (13) 图4 BiLSTM网络结构Fig.4 Network structure of BiLSTM 本研究所利用的历史气象和功率数据来自沙漠知识澳大利亚太阳能中心(Desert Knowledge Australia Solar Centre, DKASC)13号光伏电站的数据库. 该光伏系统的最大功率为5.25 kW. 从DKASC网站[30]数据库上下载2013-04-24—2022-03-23的历史气象和功率数据. 所下载的原始数据包括: 功率P(kW)、 斜面漫反射辐照度(RDT, W·m-2)、 环境温度(℃)、 相对湿度(%)和累计降雨量(mm). 13号电站所在地区的数值天气预报(numerical weather prediction, NWP)数据来自Weather Underground网站[31]数据库, 包括环境温度(°C)、 相对湿度(%)和累计降雨量(mm). 首先, 经下采样处理, 使得DKASC和Weather Underground数据的分辨率一致. 经下采样后, 总体数据去除缺失值和异常值, 再归一化. 其次, 根据2DGRA和BiLSTM的输入格式要求, 将数据重构为三维张量, 如图5所示. 第一个维度对应天数, 第二个维度对应每天48个采样点, 第三个维度对应特征的数量. 图5 数据重构三维张量Fig.5 Three dimensional tensor reconstruction of data 最后, 根据日功率曲线的波动性将历史数据分为3种类别: 晴空条件、 轻度非晴空条件和重度非晴空条件. 图6展示3种分类下的日功率曲线, 横坐标时间步长为30 min, 纵坐标最大系统功率5.25 kW. 如图6所示, 晴空条件对应光滑的日功率曲线, 天气类型常为晴天. 轻度非晴空条件对应在光滑曲线的基础上存在轻微波动的日功率曲线, 天气类型常为阴天. 而重度非晴空条件对应波动较大的日功率曲线, 天气类型常为雨天. 图6 日功率曲线3种分类Fig.6 Three weather classification daily PV power curve 为验证所提出2DGRA-BiLSTM模型在日功率曲线预测的性能, 本研究同时设置BiLSTM[29]、 2DGRA-LSTM[27]、 LSTM[28]和2DGRA-BP[32]模型作为对比模型. 文中所有模型都是基于Python 3.8.3和Pytorch 1.4.0实现的. BiLSTM模型由3层128神经元的双向LSTM层和2层64神经元的双向LSTM层构成, LSTM模型由3层128神经元的单向LSTM层和2层64神经元的单向LSTM层构成, BP模型配置最优参数. 在数据集的划分上, 本研究将分类后的数据独立划分为训练集、 验证集和测试集3个子集, 划分比例为70%、 20%、 10%, 如图7所示. 所有实验结果皆来自于测试集的性能. 各模型训练集和验证集输入气象数据为DKASC历史气象数据, 而测试集输入气象数据为NWP数据. 图7 数据集划分Fig.7 Data set division 为了便于评估和对比本研究所提出模型的预测精度, 引入3个评价指标. 1) 平均绝对误差(mean absolute error,EMA). 其计算式为 (14) 2) 均方根误差(root mean square error,ERMS). 其计算式为 (15) 3) 决定系数(R2). 其计算式为 (16) 表1展示了3种天气分类下不同模型在测试集上的预测精度. 表1 晴空、轻度非晴空和重度非晴空条件下不同模型预测精度 晴空条件下, 5种预测模型都表现出了较高的预测精度, 5种模型间的预测性能差距较小. 这是由于晴空条件下的光伏功率是一条简单的光滑曲线, 基本不存在波动, 各个模型只需实现对光滑曲线的幅度和偏置进行预测即可, 相对容易. 在轻度非晴空和重度非晴空条件下, 本研究所提出的2DGRA-BiLSTM模型有着最高的预测精度. 通过表1中的精度对比, 所提出2DGRA-BiLSTM模型在轻度非晴空和重度非晴空条件下均表现出了更佳的预测精度. 在所有模型都展现出高精度的晴空条件下的预测精度虽与2DGRA-LSTM模型存在细微差距, 但综合应对不同场景的预测性能更强. 总体上来说, 通过2DGRA获取的相似日信息的加入, 能够有效提高预测精度. 同时, 具有双向传递特性的BiLSTM预测精度比单向的LSTM高. 为了更加直观比较不同模型在预测精度上的差距, 图8展示了不同天气类别不同模型的日功率曲线预测结果和对应实际功率的对比. 由图8可知, 在晴空条件下, 由于日功率曲线相对光滑, 所有模型的预测值均能较好地接近实际功率, 模型间精度差距较小; 而在非晴空条件下, 随着非晴空程度的加深, 日功率曲线的波动性增强, 2DGRA-BiLSTM模型的相对预测性能更加突出. 图8 3种天气分类下不同模型对日功率曲线预测的对比Fig.8 Comparison of daily power curve prediction of different models under three weather classifications 为实现日前光伏功率曲线精准预测, 提出一种2DGRA-BiLSTM模型. 其中, 2DGRA用于获取最佳历史相似日, BiLSTM模型用于实现气象数据和相似日数据对第二天光伏功率日曲线的回归预测. 相比已有研究, 将相似日的获取方法从GRA改进为2DGRA, 并引入能够有效进行功率曲线预测的BiLSTM网络. 为验证所提出模型的有效性, 实验分别设置BiLSTM、 2DGRA-LSTM、 LSTM和2DGRA-BP模型作为对比模型. 所有模型皆通过DKASC历史气象和功率数据进行训练, 并通过NWP和功率数据进行测试. 实验结果表明: 在晴空条件下所有模型都能够较好地预测功率曲线; 而在轻度与重度非晴空条件下所提出2DGRA-BiLSTM模型R2分别为0.940和0.782, 相对预测精度更高, 且性能优势随着非晴空程度的加深而扩大.2.2 双向长短期记忆神经网络
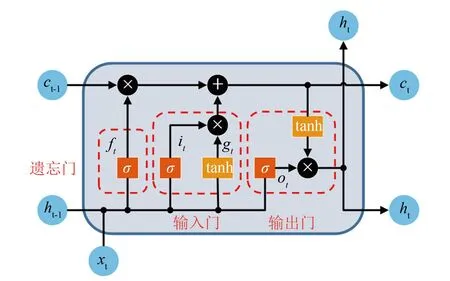

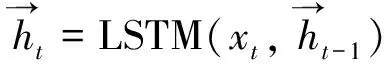

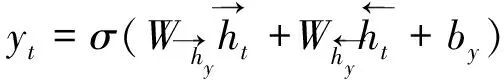
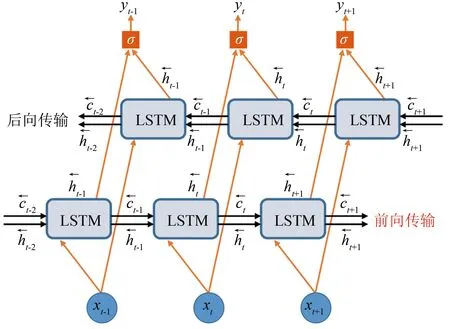

3 实验仿真
3.1 实验数据
3.2 数据预处理
3.3 超参数设置和模型训练
4 实验结果与分析
4.1 评价指标

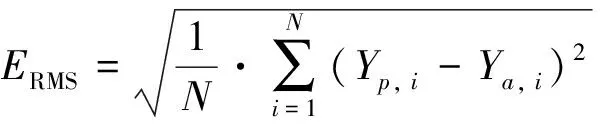
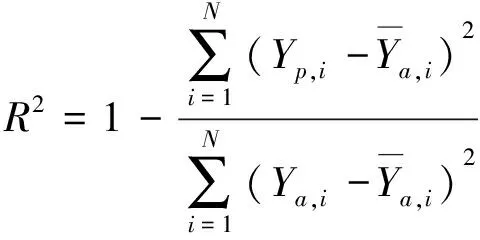
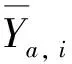
4.2 实验结果对比
5 结语

