基于曲率图卷积的非均匀点云掩码自编码器
黄敏明, 傅仰耿
(福州大学计算机与大数据学院, 福建 福州 350108)
0 引言
在点云相关任务中, 由于3D数据标注比2D数据标注成本更高, 其自监督预训练具有更高的研究价值. 数据增强是自监督学习中的重要环节, 如文献[1]中提出的Occlusion Completion(OcCo)算法使用被遮挡的点云作为增强数据, 文献[2]中提出的DepthContrast算法对输入点云进行随机裁剪和随机丢弃. 为更好地训练编码器的特征提取能力, 有研究提出更加复杂的点云数据增强方式. 文献[3]对同一场景中不同视角的点云进行刚体变换. 文献[4]将两种不同的点云混合在一起, 然后从混合点云中分离出原始点云来预训练点云特征提取器.
然而, 模型通过这些数据增强方式无法学习到物体局部结构与整体结构之间的关系, 这限制了编码器的特征提取能力. 文献[5]中提出的Point-BERT算法通过将掩码随机分组并预测不同分组对应的离散编码, 促使编码器去学习局部结构与整体结构之间的关联. 但是, Point-BERT算法需要先预训练一个离散变分自编码器, 来完成从局部结构到离散编码的转换, 并且掩码token也会被输入到编码器中, 导致位置信息的泄露, 并增加训练的显存消耗. 最近, 文献[6]中提出的点云掩码自编码器Point-MAE, 通过将掩码token直接输入解码器来预测被掩码的分组点云, 从而解决了上述问题, 并在下游任务中取得了很好的效果. 但点云掩码自编码器仍存在两点不足: 1)由于采用最远点采样进行均匀分组, 使得复杂结构与简单结构上的分组数量无明显差异, 复杂结构上的分组数量不足, 无法提供足够的信息来帮助模型学习复杂结构的几何特征, 而简单结构上的分组数量又将过多; 2)使用均匀分布进行随机掩码意味着不同几何结构复杂度上的分组有相同的学习权重, 给予简单几何结构上的分组过多的学习权重, 将使模型学习到更多的冗余信息.
为提高模型对复杂结构的学习能力并减少冗余, 本研究提出非均匀掩码自编码器(Nonuniform-MAE). 首先, 利用图卷积强大的局部特征提取能力来学习局部节点重要性度量. 为此, 提出一种新的点云上的图卷积, 即曲率图卷积(curvature graph convolution, CurvConv); 然后, 引入图池化降采样进行非均匀分组, 提高模型对复杂几何结构的学习能力. 最后, 根据每个分组的局部特征来动态调整其掩码概率, 以避免在简单结构上分配过多学习权重而导致模型学习到更多的冗余信息.
1 基于曲率图卷积的非均匀点云掩码自编码器
非均匀掩码自编码器的整体框架如图1所示. 点云输入模型后首先需要经过两层曲率图卷积模块提取高维特征. 其次, 通过图池化层进行降采样, 得到分组中心节点特征和节点下标(idx), 并输入一个基于多层感知机的增强器(multi-layer perception, MLP)来学习每个分组的掩码概率. 再次, 根据掩码率对掩码概率最大的一部分分组进行掩码, 得到可学习的掩码分组. 最后, 将未被掩码的分组进行编码, 得到高维度特征信息.

图1 基于曲率图卷积的非均匀点云掩码自编码器架构图Fig.1 Structure of curvature graph convolution based nonuniform point cloud masked autoencoders
1.1 曲率图卷积
点云上的图卷积最常用的邻居节点查询方法包括K最近邻(K-nearest neighbor, KNN)和球查询. 例如, EdgeConv采用KNN固定查询k个最近邻居节点[8], PointNet++采用固定的查询半径进行球查询[9]. 然而, 对于点云中不同节点, 其邻居查询范围应根据不同的局部几何特征进行调整. 现有方法限制了图卷积在点云上的特征提取能力. 为此, 在GCN[10]和EdgeConv[8]的基础上, 提出基于曲率的图卷积, 根据每个点的平均曲率来动态调整其邻域范围.
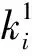
(1)
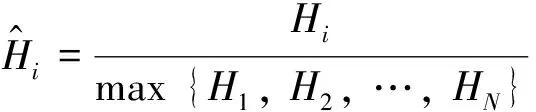
(2)
将平均曲率与球查询相结合, 提出曲率球查询, 在点云查找邻居节点, 如图2(a)所示. 对于第i个节点, 其查询邻域半径范围(ri)与其曲率大小成正比, 曲率越大, 对应的查询半径也越大.ri的表达式为
(3)

图2 曲率图卷积邻域构建示意图Fig.2 Neighborhood construction of curvature graph convolution
式中:r为初始化半径.
将平均曲率与KNN结合提出曲率K最近邻, 如图2(b)所示. 对于第i个节点, 查找其nk个最近邻节点(n表示最大搜索范围倍数), 并根据节点i的曲率计算其空洞卷积跳过节点数(di).最后, 每隔di个节点选取一个节点, 直到选取满k个邻居节点为止.di的计算公式为
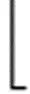
(4)
根据公式(3)和(4)可知, 点云节点的曲率越大, 对应的曲率K最近邻节点跳过节点数或者曲率球查询的搜索半径越大. 这使得图卷积操作能够聚合更大范围的邻居节点特征信息, 从而提高特征提取能力.
1.2 非均匀分组与掩码
1.2.1非均匀分组
受Graph U-Nets[12]启发, 通过曲率图卷积提取点云特征矩阵, 可表示为
Fl=CurvatureConv-Blocks(Ainput,Finput)
(5)
式中:Fl表示第l层节点的特征矩阵;Finput∈RN×3, 为输入点云坐标矩阵;Ainput∈RN×N, 是在点云上构建的图的邻接矩阵; CurvatureConv-Blocks表示l层曲率图卷积组成的特征提取模块.
接着, 根据特征学习节点的重要性度量, 通过一个多层感知机(MLP)对节点特征维度进行转换, 并通过激活函数tanh求得每个节点的重要性度量分数. 即
y=tanh(MLP(Fl)) (y∈RN×1)
(6)
并通过下式对公式(6)计算得到的分数进行排序, 得到前Npooling(Npooling idx=rank(y,Npooling) (7) 式中: rank表示排序函数. 再通过select函数从矩阵Fl中根据下标选出对应的元素, 并组成新的矩阵Fpooling用来表示池化后图的节点特征. 即 Fpooling=select(Fl, idx) (8) 在此基础上, 按照下式从输入点云矩阵中根据池化图节点下标选出分组中心节点矩阵(FCT). 即 FCT=select(Finput, idx) (FCT∈RNpooling×3) (9) 最后, 通过KNN算法在输入点云矩阵中计算出不同的分组结果矩阵(P). 即 P=KNN(Finput,FCT) (P∈RNpooling×k×3) (10) 式中: 每个分组中有k个点. 在最终的分组结果中, 位于复杂结构上的分组数量较多, 而位于简单结构上的分组数量较少. 1.2.2非均匀掩码 根据1.2.1中的描述, 可以得到分组结果矩阵(P).对于任意分组pi∈P, 将与一个掩码概率mi∈M相关联, 其中M表示所有分组对应的掩码概率矩阵, 其计算公式为 M=sigmoid(MLP(Fpooling)) (11) 式中: sigmoid表示激活函数. (12) 实验使用Ubuntu 18.04操作系统. 实验硬件环境如下: 内存为64 GB; 显卡为NVIDIA RTX A4000; CPU型号为6×Xeon Silver 4310@2.1 GHz. 实验中用到的工具包括Python3.7、 CUDA 11.1、 cuDNN 8.0.5和Pytorch 1.8.1. ModelNet40数据集有12 311个CAD模型, 包括40种不同类型点云. 将9 843个点云划分为训练集, 2 468个点云划分为测试集. 在本研究中的同等实验条件下, Point-MAE只达到93.3%的精度(A1). 这可能是由设备环境差异和文献[6]中未提及的训练方法、 超参数设定导致的. 实验旨在验证本研究提出的方法在同等条件下能够提高点云掩码自编码器在下游分类任务中的表现, 结果如表1所示. 表1 ModelNet40数据集点云分类 本研究提出的Nonuniform-MAE在自监督学习中优于目前的主流方法. 并且使用曲率图卷积能够进一步提升Nonuniform-MAE分类精度, 达到93.7%, 与Point-MAE相比提高0.4%, 与使用EdgeConv作为特征提取器的Nonuniform-MAE相比提高0.2%. 这一结果表明基于曲率图卷积的非均匀掩码自编码器能够在分类任务中很好地泛化. 表1括号中的Edge表示使用EdgeConv作为特征提取器, 括号中的Curv表示使用本研究提出的曲率图卷积作为特征提取器. 由于Completion3D数据集的测试集中并未提供完整真值点云, 需要将补全后的点云上传至指定网站才可计算得到补全精度, 给模型的训练与测试造成一定的不便. 为此, 本研究在Completion3D数据集的基础上提出Completion3Dv2数据集, 根据TopNet中的定义, 从PCN数据集的完整真值点云中重新降采样获取2 048个点的标准真值点云, 并保持与PCN数据集完全相同的训练集、 验证集和测试集划分. 在此基础上, 从[1, 0, 0]、 [0, 0, 1]、 [1, 0, 1]、 [-1, 0, 0]、 [-1, 1, 0]这5个点中随机选取1个作为中心点, 对Completion3Dv2中的完整真值点云进行裁剪, 取其最近邻512个点作为缺失点云, 剩下的1 536个点作为残缺点云. 实验结果如表2所示, 采用L2倒角距离衡量补全精度(A2), 值越小则补全精度越高, 所有值均放大104倍. 将CurvConv+Nonuniform-MAE与PoinTr结合, 最大能够提高0.21的补全精度, 优于目前主流的补全模型. 并且CurvConv+Nonuniform-MAE的补全效果优于Point-MAE. 这一结果表明非均匀掩码自编码器Nonuniform-MAE的预训练效果优于点云掩码自编码器, 能够有效提高点云补全效果. 表2 Completion3Dv2数据集点云补全精度 为验证曲率图卷积、 非均匀分组和非均匀掩码的有效性, 在预训练过程中分别使用EdgeConv、 最远点采样均匀分组和随机掩码进行逐个替换. 使用预训练编码器代替PoinTr中的编码器, 进行补全实验. 结果如表3所示, 与使用EdgeConv相比, 使用CurvConv能够进一步优化预训练效果, 并将总体补全精度提高0.11, 表明曲率图卷积的有效性. 在相同条件下, 使用非均匀分组能够提高0.29的补全精度, 而使用非均匀掩码能够提高0.16的补全精度. 由于非均匀分组模块作为点云输入模型后的第一个处理模块, 其特征提取能力和分组的有效性将直接影响后续所有步骤, 因此非均匀分组对补全精度的提高效果更加明显. 表3 非均匀掩码自编码器不同组件有效性对比 为探究不同的掩码率(γ)对预训练效果的影响, 分别将γ设置为50%、 60%、 70%和80%, 进行预训练, 并将预训练后的编码器代替PoinTr中的编码器进行补全实验, 得到的补全精度分别为5.84、 5.08、 5.47、 6.11. 在掩码率为60%时, 可取得最好的补全效果; 当掩码率低于60%或者超过70%时, 补全效果都有较大幅度的降低. 提出一个基于曲率图卷积的非均匀掩码自编码器, 通过节点曲率来动态调整邻域范围以提高图卷积的局部特征提取能力, 并在此基础上结合图池化进行非均匀分组和掩码来动态调整不同结构的学习权重, 避免模型学习到过多的冗余信息. 将经过本文方法预训练的编码器用于点云分类和补全任务, 均取得较好的结果, 验证了本算法的有效性. 本研究中被掩码的分组数量是固定值, 并且在曲率图卷积中主要采用平均曲率进行计算. 因此, 如何动态调整被掩码的分组数量以及如何结合主曲率、 高斯曲率进一步优化曲率图卷积将是今后研究工作的主要目标.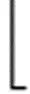

2 实验结果与分析
2.1 实验条件
2.2 点云分类实验

2.3 点云补全实验

2.4 消融实验

3 结语

