国际数学教育研究的知识基础与前沿——基于2018—2022年数学教育国际期刊的文献计量分析

郑国强，谢圣英

国际数学教育研究的知识基础与前沿——基于2018—2022年数学教育国际期刊的文献计量分析

郑国强，谢圣英

（湖南师范大学 数学与统计学院 计算与随机数学教育部重点实验室，湖南 长沙 410081）

国际数学教育领域的年发文量整体呈上升趋势，通过文献计量分析发现：依托方法论书籍、教育政策文件、研究手册和关键文献提供的知识基础，国际数学教育研究前沿聚焦于“数学过程”“数学内容”“数学教与学的环境”以及“数学教师教育”4个方面；研究围绕PISA数学框架考察数学认知、能力和素养，建立了小学、中学和大学相邻学段的数学学习衔接性的关键纽带；关注从社会文化差异的视阈审视数学教与学的环境因素，并维持了“数学教师教育”自21世纪以来一直成为研究前沿的地位．中国应增强文化批判意识，评估国际数学教育研究前沿，开展本土化的数学教育研究，并加强教育研究和实践的沟通．

数学教育研究；知识基础；国际研究前沿；本土化研究；文献计量分析

1 问题提出

目前，中国数学教育研究发展迅速，取得了一系列显著成就，创造了具有中国特色的数学教育理论与实践．与此同时，也成功创办了一些高水平的中文学术期刊，诸如《数学教育学报》《数学通报》等．但近代以来，相比于西方，中国数学教育研究的整体水平存在一定差距[1]．在突出中国特色数学教育的基础上，了解国际研究前沿，加强合作与交流，是实现中国数学教育现代化、加速发展数学教育事业的可行途径．作为新一代的数学教育研究者，尤需明晰领域核心问题，“放眼世界，立足本土”[2]．

数学教育国际研究前沿一直受到国内学者的关注，一般通过学术会议管窥研究进展，诸如国际数学教育大会（ICME）、国际数学教育心理学大会（PME）以及国际数学教材研究与发展会议（ICMT）．也有学者通过翻译和梳理文献，了解国际研究的经典理论与发展趋势，为建设中国数学教育事业提出建议．这些研究主要集中于微观和中观层面，涉及文献知识图谱探析的宏观研究相对较少．同时，已有的研究主要依托高频关键词来剖析国际研究现状[3-5]，着眼于国内数学教育研究的特征与热点[6-7]，基于《数学教育学报》《数学通报》作载文分析[8-9]，而以共被引关系为切入点探求国际研究前沿的文献有待进一步丰富．基于此，研究者旨在考察近几年刊出的国际期刊论文，厘清国际数学教育研究的知识基础与前沿，助力中国数学教育研究前沿化、本土化．

2 研究数据与方法

2.1 数据收集

为提高检索结果的信效度，真实反映国际数学教育的最新研究进展，以影响力较大的9份数学教育国际期刊为限定，时间跨度为2018年1月1日—2022年10月1日，累计检索文献3 271篇．筛选出“论文”“综述论文”，并作去重处理后，最终得到有效文献2 891篇，作为文献计量分析的来源数据．所选9份数学教育国际期刊的相关信息如表1．

表1 9份数学教育国际期刊及其类别与文献占比

注：SSCI（Social Sciences Citation Index）、ESCI（Emerging Sources Citation Index）期刊索引来源为2022年Web of Science．

2.2 研究方法和工具

文献计量分析通常借助科学知识图谱对已发表的文献进行整体的可视化与统计分析，它突破了单篇文献的局限，从更高的视野寻求新的知识发现．使用VOSviewer1.6.18建构作者、机构和国家/地区的合作网络图谱，了解国际数学教育的研究主体，并利用CiteSpace6.1.R3绘制参考文献的共被引网络聚类及突现图谱，探寻数学教育研究的知识基础和国际前沿．

3 国际数学教育文献分布特征

3.1 总体发文趋势

限定期刊的数学教育文献年发文量整体呈上升趋势（如图1）．2018—2020年，文献数量不断增长；2020—2021年，发文量波动较为平缓，保持在每年700篇左右．从单个期刊看，除了、和每年的文献数量相对稳定，其它期刊年发文量基本保持增长态势．不同期刊的发文数量差异较大，这与刊期和单期载文量有直接关系．

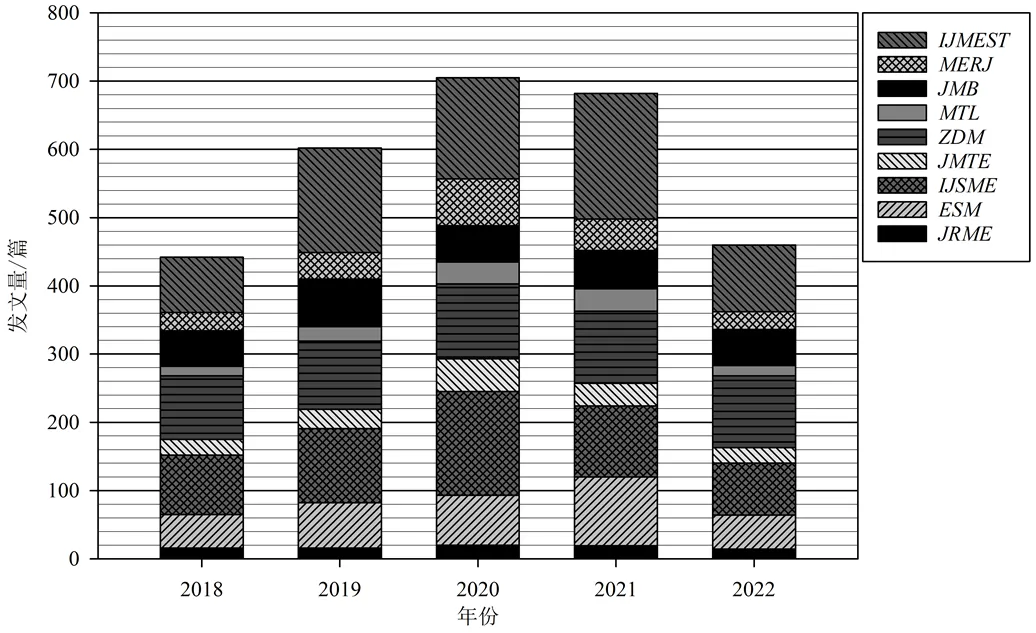
图1 限定的数学教育期刊的文献年度分布

3.2 研究作者与机构及国家/地区

通过统计作者、研究机构和国家/地区的发文量、被引频数以及合作数，可以确定从事国际数学教育研究的主体，从而更全面地反映该领域的发展状况．

文献作者层面，发文量和被引频次均居前10的作者有：Gabriele Kaiser（德国汉堡大学）、Jinfa Cai（美国特拉华大学）、Susanne Prediger（德国多特蒙德工业大学）、Keith Weber（美国新泽西州立罗格斯大学）、Lieven Verschaffel（比利时鲁汶大学）和Stanislaw Schukajlow（德国明斯特大学）．其中以美国和德国学者居多，累计被引频数达752次，各自建立的合作关系也相对较多．一般地，衡量学者之间合作情况的指标有两项：合作度（单篇论文作者数）与合作率（合著论文的占比）[10]．2 891篇检索的有效文献中有509篇为独著论文，限定期刊的作者合作度约为1.6人次／篇，合作率约为82.4%．其中，每年的合作情况较为稳定，合作率保持微小的增长趋势．

研究机构层面，选择发文量不少于10篇的机构绘制合作网络图谱，累计发文量占总文献的78.04%．这些机构通常是国际数学教育研究成果的重要产出机构，主要为综合性高等院校．其中，澳大利亚莫纳什大学和凯斯林大学、以色列海法大学以及德国汉堡大学的发文量、被引数与合作机构数排名均居前10．国家/地区层面，美国、德国、澳大利亚、英国、加拿大和西班牙的发文量、被引次数与合作国家数排名均居前10．美国的3项指标均第一，且第二名与其差距较大．就整体研究实力和影响力而言，美国占据首要地位．

4 国际数学教育研究可视化分析

选择每年被引频次排名前50的文献，利用Citespace软件根据LLR聚类算法，以关键词作为聚类提取术语，绘制共被引网络图谱．生成的聚类模块性比较显著，聚类内部的同质性较高，结果具有高信度[11]（Modularity=0.852 9>0.3，Silhouette=0.939 7>0.7）．

从研究发展的视角看，几乎所有领域的研究都需建立在先前研究的知识基础之上，以保持研究演进的连续性．知识基础是由共被引文献集合组成的，而研究前沿是由引用这些知识基础的施引文献集合组成的[11]．因此，借助共被引分析结果，了解国际数学教育研究前沿的知识基础，有助于把握研究领域的整体发展脉络．

4.1 国际数学教育研究的知识基础

4.1.1 高被引文献

高被引文献统计结果（见表2）显示，被引前10的文献类型主要为著作（6本）、著作章节（2篇）和期刊论文（2篇）．著作主要为方法论指导书籍，涉及扎根理论、案例研究等质性研究方法，内容涵盖研究的设计、数据分析方法、编码及操作程序，表明国际数学教育侧重于实证研究，质性研究方法是主流的方法论基础；其次为政策性文献，如全美数学教师理事会（NCTM，2014）发布的《行动原则：确保所有学生数学成功》和美国数学教师教育工作者协会（AMTE，2017）发布的《数学教师培养标准》等，揭示出数学教育研究具有政策导向性．著作章节方面，Thompson和Carlson（2017）讨论变化和协变推理以及函数概念的文献被引频数最高，达64次，它与《证明的教与学研究：回顾与展望》（Stylianides & Stylianides，2017）综述论文共同收录于《数学教育研究手册》（）．还有两篇高被引期刊论文分别探讨了数学教育中的身份研究以及STEM教育．

表2 高被引文献统计表（被引频次前10）

注：表中只记录了文献的第一作者，表3同．

4.1.2 高中介中心性文献

除被引频数以外，中介中心性可作为衡量文献重要性的另一个指标．“具有高的中介中心性的文献可能是连接两个不同领域的关键枢纽”，被称为转折点[11]．统计中介中心性前10的文献，如表3所示．

表3 高中介中心性文献统计表

其中，《数学建模的教与学》（Kaiser，2017）与《学生建模能力的创造性：概念化与测量》（Lu & Kaiser，2022）存在共被引关系，二者是连接数学建模和创造力领域的关键论文．《数学建模教学：联系研究与实践》（Stillman，et al，2013）促进了“非形式化统计推断”和“数学建模”两个领域之间产生联系，是网络图谱中的转折点．基于非形式化统计推断的数学建模能够创造考察概率与统计的新视角，“使用与统计思想结合的更广义的建模定义正成为一个新的研究领域”[12]．此外，《为工作场所的素养做准备：建模视角》（Wake，2015）列举了“铁轨坡度”“债务天数”“舞蹈动作”“歌手海选”等跨学科背景下的建模案例，探讨实际工作场所中所需要的数学能力和素养[13]，促进了数学建模与STEM教育的融合．

4.1.3 突发性文献

如果高被引文献体现了经典范畴，那么突发性文献则反映活跃领域．共被引网络图谱中，某个聚类所包含的突发节点越多，那么反映该领域就越活跃，也可能是研究的新兴趋势[11]．绘制突发性强度前25的文献列表，借助摘要、关键词等内容概括出核心主题，国际数学教育较多地使用案例研究等质性研究方法（3篇文献），研究内容上表现为数学教师教育领域较为活跃，涉及教师知识、能力以及教师专业发展（6篇文献），其中“教师关注”主题就包含了3篇突发性文献，在数学教师教育领域内较为突出（见图2）．

4.2 国际数学教育研究前沿

文献共被引聚类图谱如图3所示，通过梳理文献，选择较大的聚类并对其中相似聚类进行整合后发现，国际数学教育研究前沿涉及12个主要领域：数学教育研究理论（#0、#8、#15）、数学创造力（#1）、数学问题提出（#5）、数学建模（#12、#19）、数学推理（#2、#11、#13）、社会文化研究（#3、#4）、教师关注（#6）、STEM教育（#7）、大学数学（#9、#20）、数学教科书（#10）、早期代数（#16、#18）以及数学教学质量（#17）．

4.2.1 数学教育研究理论（Theory in Mathematics Education Research）

本领域主要凸显了3个核心理论：变异理论（Variation Theory）、交流认知（Commognition）和反省抽象（Reflective Abstraction，又称“自反抽象”）．其中，变异理论是由瑞典学者Marton所建立的教学与学习理论，与中国提倡的变式教学理论有相似之处[14]．该理论多作为教学实证研究中干预措施的实施依据，学生知识理解和学习以及数学课堂教学分析的理论依据．也有研究者从变异理论的视角出发，倡导使用多元表征方式来设计有关图形（如笛卡儿坐标系）的数学任务[15]．第二个理论——交流认知，是以色列学者Sfard基于“学习即参与”的假设提出的一种“社会文化取向”的理论，用于数学课堂互动作话语分析[16]．近期有研究考察动态几何环境下中学微积分开放式任务解决过程中的互动，利用交流认知理论分析学生的语言交流和触摸屏上的拖动手势[17]．第三个理论——反省抽象，是指将个体操作中的关系进行“投射”和“反射”的过程，皮亚杰用其阐述个体对数学抽象活动的认知[18]．Simon研究团队借助反省抽象建构“通过活动学习”（Learning Through Activity）的理论框架，用以解释教学设计与数学概念的学习[19]．

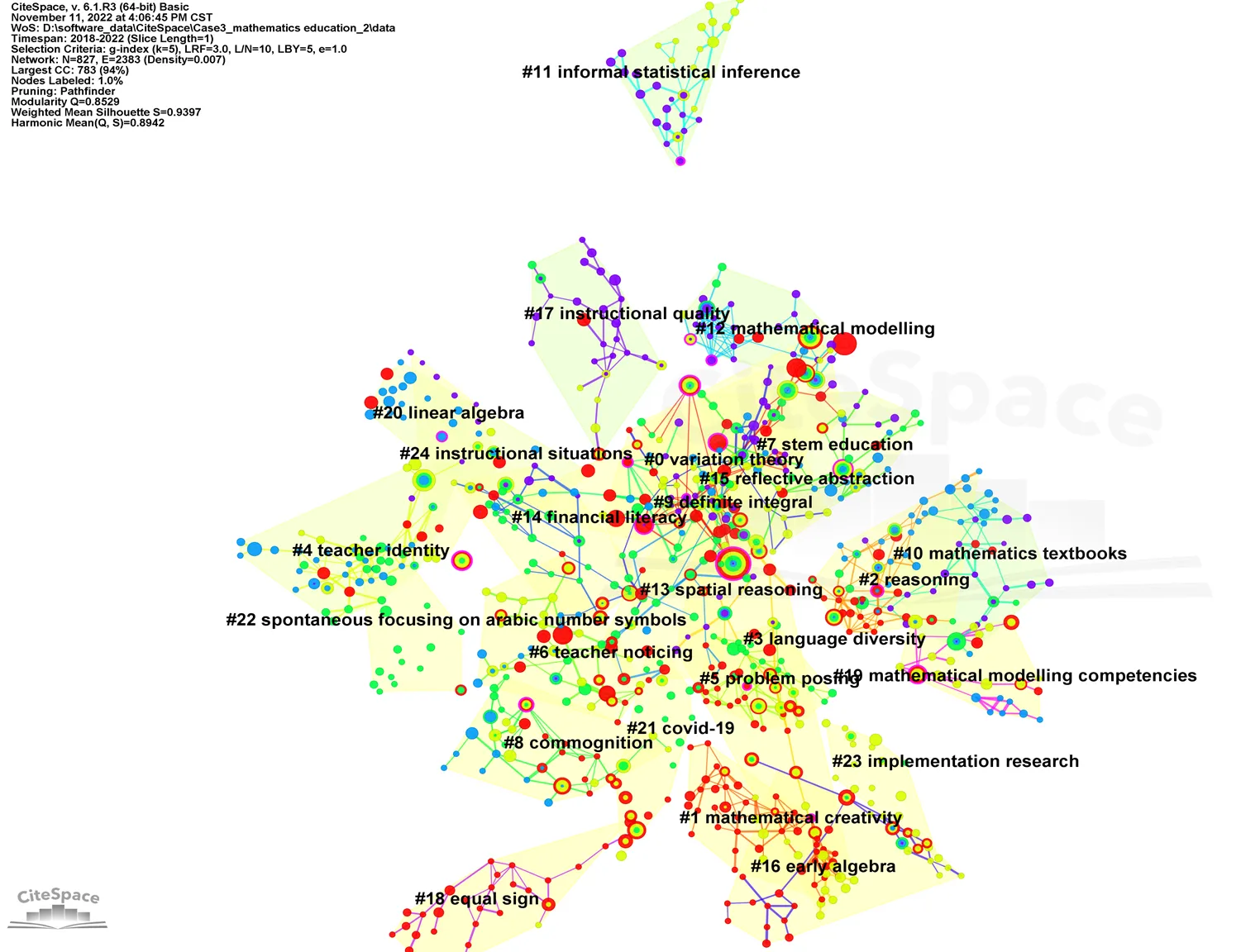
图3 共被引聚类图谱

4.2.2 数学创造力（Mathematical Creativity）

数学创造力相关研究主要围绕3个方面展开．第一，考察问题提出与问题解决中的创造力．有研究探讨实施问题提出干预能否促进三～五年级学生数学创造力的提高[20]；还有研究者选取荷兰三～六年级学生作为研究对象，研究他们解决封闭式常规问题、封闭式非常规问题和开放式非常规问题的表现与数学创造力的关系[21]．第二，数学集体创造力研究．比较高中生解决开放式几何任务时，个人创造力与集体创造力表现的差异，以及有无小组学习经历对创造力表现的影响[22]．第三，探究数学创造力与数学建模能力[23]等其它因素的关系．

4.2.3 数学问题提出（Mathematical Problem Posing）

有关数学问题提出的文献比较丰富，部分研究侧重探讨问题提出的表现与过程．如从学习轨迹的视角考究年级与问题情境是否会影响中国初中生的数学问题提出表现[24]，Baumanns和Rott（2022）开发了结构化情境问题提出的描述性阶段模型，分为情境分析、变化、生成、问题解决和评估5个阶段[25]．也有研究尝试探索问题提出的教学，如Cai和Hwang（2021）通过教师专业发展项目，开展使用问题提出教授数学的实践研究[26]．还有一些研究关注不同情境或数学内容领域的问题提出，论及针对真实生活情境的数学建模问题的提出及其解决[27]等．此外，影响问题提出的非智力因素亦是研究的焦点．譬如，通过收集中国苗族学生的实证数据，并借助期望价值理论（Expectancy-value Theory）来阐述问题提出表现分别与自我概念、内在价值和考试焦虑等情感因素之间的关系[28]．

4.2.4 数学建模（Mathematical Modelling）

数学建模研究一方面基于包含社会—认识论[29]在内的不同视角，审视数学建模及其过程；另一方面探究数学教师的建模知识、能力、态度和观念，相关讨论比较广泛，其中一项研究比较了中国和德国职前数学教师有关建模的内容知识和教学内容知识的能力水平[30]，也有研究致力于开发和评估教师对数学建模的态度量表[31]．此外，还有数学建模任务的设计、实施与解决的相关研究．如着眼于虚拟学习环境中数学建模项目（或课程）的开发[32]，以及探讨在中国和德国的不同教育环境下，阅读理解提示在数学建模问题解决中的作用[33]．

4.2.5 数学推理（Mathematical Reasoning）

数学推理的前沿研究包含非形式化统计推断（Informal Statistical Inference）、空间推理（Spatial Reasoning）、比例推理（Proportional Reasoning）、定量推理（Quantitative Reasoning）、协变推理（Covariational Reasoning）等．具体而言，非形式化统计推断研究该主题背景下学生的统计推理与建模学习．也有研究探究小学职前教师非形式化统计推断内容知识的认知与发展[34]．空间推理与STEM教育密切相关，研究集中于将其作为干预措施评估对学生数学学习的影响．比例推理研究主要考究教师如何理解和认识比例推理，如何解决线性或非线性比例推理问题，以及解决过程中知识资源的使用．也有研究立足于六～八年级学生，剖析其解决现实生活情境的比例推理问题的策略、困难以及产生困难的原因[35]．关于定量推理，有学者考察本科生在解决微积分中的相关变化率问题（Related Rates Problems）时是如何看待图象对理解量及其关系的帮助作用的[36]．此外，协变推理主题的研究围绕职前教师协变推理的发展，协变推理的教学，以及学生在数学任务解决中如何使用协变推理等问题．

4.2.6 数学教育社会文化研究（Sociocultural Research on Mathematics Education）

对“建构主义”的讨论在20世纪八九十年代达到顶峰，其后受关注程度逐渐下降，而“社会文化理论”的突出性逐渐增大[37]，这种“社会转向”（Social Turn）或“社会政治转向”（Sociopolitical Turn）促进了数学教育中的公平、身份等关键领域的发展[38]．近年来，社会文化研究的前沿为语言（Language）和身份（Identity）．

“语言”主题，国际学者就语言的多样性及其在数学学习中的作用进行了相关探索，包括第二语言、双语或多语言背景下的数学学习，以及不同语言环境中的数学学习比较．此外，许多文献探讨语言对数学任务解决的影响．如借助眼动追踪（Eye Tracking）来分析中文和德文语境下数学应用题的解决[39]，以及调查学生语言能力和任务语言措辞对解决建模问题的影响[40]．

“身份”主题，主要研究对象为数学教师．已有文献多使用质性研究方法，数据来源多为访谈、书面叙述和课堂观察[41]．依托不同理论，侧重于审视教师身份的概念化，探析数学职前教师、在职教师和教师教育工作者的身份形成与发展．也有研究致力于开发和评估数学教师身份量表[42]．另外，学生的数学身份也是研究者讨论的方向之一[43]．

4.2.7 教师关注（Teacher Noticing）

“教师关注”是数学教师专业发展研究的分支，考察教师的思维以及教师对学生数学思维的注意，具体涉及探索教师关注的概念化．绝大多数研究从认知的角度进行概念界定，但也有研究从社会政治[44]等视角审视教师关注．研究方法多为质性研究和混合型研究[45]，许多研究借助视频相关工具作为考察教师关注的手段[46]．研究对象大体分职前、初任和专家型教师3类，在特定情境或视角下比较某类教师内部、3类教师之间或不同国家教师之间的教师关注差异．

4.2.8 STEM教育（STEM Education）

STEM教育研究基本围绕3方面展开：STEM教师教育、STEM项目（或活动）的教与学以及数学在STEM教育中的作用．如分析职前教师对STEM活动提出的课程建议，讨论STEM教育的数学职前教师培养[47]；使用行动研究探索实施以创客为中心的、基于STEM项目的学习为一所台湾省农村中学带来的改变[48]；还有研究提出要加强STEM学习与“21世纪技能”（21st Century Skills）的获得、数学建模、负责任的公民教育之间的联系，以提升数学在STEM教学中的作用[49]．

4.2.9 大学数学（Undergraduate Mathematics）

大学数学涵盖微积分和线性代数两个主题．相关概念的理解是微积分研究中的一个焦点，已有研究运用APOS理论作为分析框架，剖析学生对极限、隐函数、导数、积分等概念的理解．其它研究主要窥探微积分的学习问题．一方面，有学者研究数字技术支持的微积分基本定理学习中的学生意识焦点[50]，以及翻转课堂[51]等情境中的微积分学习；另一方面，探究高中与大学微积分学习的过渡和联系，着重评估高中数学教育能否为学生在大学学习微积分提供充足准备[52]．线性代数研究主要关注线性代数的教与学：前者侧重于探寻支持线性代数教学的工具，阐述几何直观化、数学建模和信息技术在线性代数教学中的作用[53]；后者涉及借助APOS理论阐释分析学生线性代数学习的心理建构[54]．

4.2.10 数学教科书（Mathematics Textbook）

“内容分析”“比较研究”等关键词包含在“数学教科书”聚类中．从内容看，研究基本集中于教科书的开发与使用以及内容分析．比如交互式教科书的设计[55]，通过调查教师对数学教科书作用的看法，探查不同类型的教科书对教师教学及其变革是促进作用还是阻碍作用[56]．从方法看，已有文献以不同国家数学教科书内容的比较为切入点，剖析教科书呈现同一数学内容的异同．其中，比较的数学内容领域囊括算术、代数与几何，也涉及问题解决和问题提出任务分布的对比．此外，教科书中数学内容的发展与变化亦是研究者感兴趣的主题．例如，分析中国小学数学6个系列的教科书中问题提出任务的分布及其变化情况[57]．

4.2.11 早期代数（Early Algebra）

早期代数研究的对象主要为小学以及初中低年级学生，研究方法多为实验研究或准实验研究．该领域内容大体上分为两类：一是立足早期代数核心内容的研究，涵盖一般化的算术（Generalizing Arithmetic）、函数关系和等号[58]；二是探讨从算术到代数过渡的相关问题．如：探析算术策略对解方程的影响[59]，且众多研究显示：小学生能够发展代数思维，有能力进行复杂的代数推理，早期引入代数概念对学生的学习有帮助[60]．

4.2.12 数学教学质量（Instructional Quality）

“数学教学”“课堂观察”等关键词出现在“教学质量”聚类中．有关教学质量的研究集中于探索数学教学质量的衡量标准，从不同的视角设计、开发和使用教学质量分析工具/框架，如基于课堂观察的教学质量框架[61]．另外，也有研究进行探索性分析，考察数学教学质量分别与教师的认知能力[62]（囊括数学内容知识、一般教学知识、诊断学生错误的速度、数学教学相关的感知、解释和决策以及课堂管理知识）、教后关注[63]（Post-Instruction Noticing）等因素之间的相关关系．

5 讨论与结论

通过梳理、、等数学教育国际期刊论文，借助知识图谱进行文献计量分析后发现，国际数学教育研究的文献年发文量整体呈上升趋势，核心研究机构主要为西方国家的高等院校，美国的综合研究影响力处于国际首要地位；国际数学教育研究前沿聚焦于“数学过程”“数学内容”“数学教与学的环境”以及“数学教师教育”．

“数学过程”包括了数学问题提出、数学创造力、数学建模和数学推理4个领域，探查数学学习中的认知、能力和素养．事实上，后3者是OECD提出的PISA2021数学框架中的重要构成要素，且框架的核心和根本目标是实际问题的解决[64]．相比于PISA以往的测评框架，PISA2021数学框架新增了“21世纪技能”这一要素，其囊括了批判性思维、创造力、交流和反思等关键能力[64]，旨在促进学生更好地应对21世纪的挑战．此要素和“数学建模”要素作为纽带共同建立起了STEM教育与PISA2021数学框架之间的联系．可以看出，除“问题提出”外，有关“数学过程”的研究前沿均紧紧围绕PISA2021数学框架来展开．该框架的内涵和构成要素值得更多地关注，特别是“21世纪技能”，未来可以进一步围绕这些要素深入展开研究，如探查批判性思维会怎样影响学校数学的学习，在提出和解决现实世界问题的过程中是如何发挥作用的，以及如何发展这一思维等．

“数学内容”方面包括大学数学（微积分与线性代数）和早期代数两个领域，关注的学段涵盖了初等、中等和高等教育，并侧重于代数领域的研究．与此结果部分类似的是，Inglis与Foster（2018）通过对与期刊论文进行主题建模后也发现，“学校代数”的关注度在上升，而“欧氏几何”的研究兴趣在不断下降[37]．具体地说，“数学内容”研究中，衔接性的教学与学习问题受到研究者的青睐，比如小学至初中的“算术思维—代数思维”的过渡，高中至大学的微积分学习的过渡．特别地，“中学—高等教育过渡”（Secondary-Tertiary Transition）主题的研究很丰富，“中学和大学之间的数学差距、促进过渡的技术潜力以及与过渡中的学业成功和学业失败相关的因素”是主要的研究焦点[65]．这些“过渡”研究为小学、中学和大学相邻学段的数学学习建立了衔接性的关键纽带，为人们更全面地认识各学段数学学习之间的关系提供了新的知识．

“数学教与学的环境”侧重于研究语言和数学教科书两个领域，二者都是承载课堂教学活动的重要载体．如前所述，不同语言背景下的数学学习比较是语言领域的研究焦点，数学教科书领域的研究着眼于多个国家教科书内容的跨文化比较．由此看出，基于社会文化差异的视阈审视教与学的环境因素是国际数学教育的一个研究趋势，也可以看作是数学教育领域“社会转向”所产生的必然结果．

“数学教师教育”包括教师关注、教师身份和数学教学质量等领域．正如Schoenfeld（2016）在展望数学教育领域未来的研究发展方向时所指出的那样，关于支持教师专业成长的研究还需要做出更多的努力[38]．而2018—2022年的研究前沿，侧重探讨身份和教师关注等有助于教师专业发展的研究领域，似乎是对Schoenfeld的建议做出回应．实际上，早在2009年，Hannula基于PME会议论文指出，1997—2007年间教师教育是最受欢迎的研究主题[66]．在最近的研究中，Gökçe和Güner（2021）梳理了相关文献并揭示出国际数学教育近四十年的研究热点，发现教师知识等教师教育领域的关键词突显出该领域仍是2010年以后的研究重点[67]．这些研究描述的内容与研究者的发现共同指向了一点：自21世纪以来，教师教育一直都是国际数学教育领域的研究前沿．

从一些文献和会议讨论的主题中，也可以捕捉到上述研究前沿的一些“蛛丝马迹”．比如，蔡金法主编的《数学教育研究手册》全面总结了国际数学教育的核心领域与前沿性问题，除了数学问题提出和数学教学质量，大部分的研究前沿以章节标题的形式包含于该手册，其中少数分散到手册各部分的讨论之中．因此，研究者发现的前沿与该手册提及的研究现状和对未来的预见相互得到了验证．另外，这些研究前沿也与ICME的研究专题存在共同的部分，呈现出了国际数学教育的最新研究趋势．ICME设定的专题研究组（Topic Study Groups，简称TSG）所讨论的主题，展示了过去、现在甚至将来数学教育的核心研究方向．纵观历届会议不难发现，从ICME-13（2016）开始，数学教育与跨学科教育、数学教科书与教学资源的研究与开发、数学教育中的社会与政治维度、数学创造力等成为新的TSG主题，且ICME-14（2021）特别新增了“数学问题提出”[68]．将于2024年举办的ICME-15预期设定了54个TSG，相比于往届会议，其特别突出了一些主题：早期代数的教与学、大学代数的教与学等[69]．这些ICME新设定或进一步突出的研究专题，反映出国际学者新近关注的领域．

综上，得出以下主要结论：依托方法论书籍、教育政策文件、研究手册和关键文献提供的知识基础，国际数学教育研究具体围绕PISA数学框架考察数学认知、能力和素养，为小学、中学和大学相邻学段的数学学习建立了衔接性的关键纽带；关注从社会文化差异的视阈审视教与学的环境因素，并维持了“数学教师教育”自21世纪以来一直成为研究前沿的地位．国际数学教育研究前沿如表4．数学教育研究理论、STEM教育为各研究层面共有的领域．

表4 国际数学教育研究前沿汇总

6 启示与展望

通过文献计量分析国际数学教育研究前沿，可以获得一些启示．

首先，应增强文化评判意识以评估国际研究前沿．了解国际数学教育的研究进展，有助于拓展研究者的视野，带来启发性的思考．但数学教育研究的目的是改进教学实践，服务于教育发展，从而研究必定要根植于本土文化的土壤．将国际数学教育理论或实践引入国内时，研究者需要深刻的文化批判意识和创造性的研究工作．国外教育理论的借鉴必须以文化比较为基础，突破“非连续性的碎片图式”，达到文化上的整体建构[70]．因此，引入国外数学教育研究前沿就是在一定程度上借鉴国外的文化，应该充分理解对方的文化理念，通过不同地域的文化比较，思索理论在国内发展“需不需要”“适不适合”“如何将其化为本土的理论”等问题，开展探索性的理论研究和验证性的实践研究．

其次，应开发本土化的数学教育研究领域．不仅要形成“本土的”研究热点和前沿，而且还要将国际前沿研究“化为本土的领域”[71]．一方面，本土研究领域的开发常常与国内教育政策或教育改革密切相关，解决实践困境是形成本土研究热点的重要方式．比如“双减”政策实施后，设计“精准而高效”的数学作业成为讨论的焦点；《义务教育数学课程标准（2022年版）》颁布后，单元教学和大概念教学成为研究热点．但是，如果注重分析比较国际国内的研究热点，则更有利于本土化教育研究领域的深耕．如比较国内数学教育研究热点[6]和国际研究前沿，中国在数学教师教育、问题提出、数学教科书等领域产出了较为丰硕的成果，可以尝试拓展到数学创造力、身份、教师关注与大学数学等领域，做出更多扎根于本土的理论和实践．再如，第二语言或双语背景下的数学学习与教学研究，或许可以为中国少数民族的数学教育提供研究借鉴；STEM教育理论、数学建模任务的解决与中国《义务教育数学课程标准（2022年版）》强调的跨学科学习相契合，相关研究或许亦有参考价值．此外，国际研究前沿的一个突出的特征是将数学教学质量作为直接的讨论对象，而不仅仅作为某个主题研究的附带阐述．国内直接讨论教学质量的实证研究相当匮乏，往往以学生学业成就水平作为指标间接衡量[72]．国际数学教育研究者借助教师课堂管理（Classroom Management）、学生支持（Student Support）和认知激活（Cognitive Activation）等多因素来衡量教学质量[62]，这种多元指标评估的方法可为国内相关研究提供参考．

最后，应加强教育研究和教育实践的沟通．虽然越来越多的研究开始关注研究与实践之间的关系问题[12]，但缩小研究与实践之间的鸿沟仍需要进一步的努力．已有研究论证，教师与研究者的伙伴关系（Teacher-Researcher Partner- ships，TRP）是一种有助于缩小研究与实践的差距的方式，能有效帮助教师学习如何更好地从事数学教学[73]．但研究结果发现，基于教师与研究者的伙伴关系来开展研究的文献还不够丰富．国内数学教育领域也存在同样的欠缺，即研究者与一线教师之间的合作相对较少[6]．

研究的文献数据源为最重要的9份数学教育国际期刊，主要进行了参考文献的共被引分析，在选取衡量文献重要性的指标时，着重探讨了被引频数、中介中心性和突发性．未来可以考虑增加共被引网络的结构变异分析的文献研究，探索核心文献在网络图谱中的影响力．此外，还可以进一步研究某一具体的国内外数学教育研究热点．

[1] 蔡铁权．中国传统文化与传统数学、数学教育的演进[J]．全球教育展望，2013，42（8）：91-100．

[2] 郑毓信．新一代数学教育研究者的成长[J]．数学教育学报，2020，29（6）：1-6．

[3] 孔企平，许自强，陈志辉，等．近十年来国际数学教育研究趋势[J]．全球教育展望，2015，44（12）：96-104．

[4] 徐柱柱，綦春霞．近二十年（1999—2018）来国外数学教育研究进展——基于WOS数据库3 061篇SSCI文献的共词分析[J]．外国中小学教育，2018（6）：72-80，46．

[5] 杨柳，郭玉峰．21世纪以来数学推理研究的国际现状与学术演进——基于CSSCI和SSCI期刊文献的对比分析[J]．数学教育学报，2023，32（2）：74-80，96．

[6] 王丽美，宋乃庆．近二十年中国数学教育研究的热点主题——基于科学知识图谱的实证分析[J]．数学教育学报，2022，31（5）：65-70，75．

[7] 梁玮，徐斌艳，于文字．近二十年国内数学高考研究进展与启示——基于CiteSpace的可视化分析[J]．数学教育学报，2023，32（2）：18-23，36．

[8] 濮安山，刘兰茵．数学推理研究三十年载文分析——以《数学教育学报》《数学通报》载文为例[J]．数学教育学报，2022，31（4）：91-97．

[9] 石义娜，吴京霖，夏小刚．近十年中国数学教育研究图景——基于《数学教育学报》（2012—2022年）文献共被引的视角[J]．数学教育学报，2023，32（2）：88-96．

[10] 邱均平，李星星．近十年来我国知识管理研究论文的统计与分析[J]．图书馆，2012（2）：71-74．

[11] 李杰，陈超美．CiteSpace：科技文本挖掘及可视化[M]．3版．北京：首都经济贸易大学出版社，2022：87-141．

[12] 蔡金法．数学教育研究手册（上册）[M]．北京：人民教育出版社，2020：33-35，518-519．

[13] WAKE G. Preparing for workplace numeracy: A modelling perspective [J]. ZDM, 2015, 47 (4): 675-689.

[14] 陈红兵．变式理论与变异理论——两个教学理论的比较与关系探析[J]．教育科学研究，2013，221（8）：22-26．

[15] JOHNSON H L. Task design for graphs: Rethink multiple representations with variation theory [J]. Mathematical Thinking and Learning, 2022, 24 (2): 91-98.

[16] 徐兆洋．“交流取向”的数学教育研究：背景、假设与概念框架[J]．外国教育研究，2018，45（3）：98-110．

[17] NG O L. Examining technology-mediated communication using a commognitive lens: The case of touchscreen- dragging in dynamic geometry environments [J]. International Journal of Science and Mathematics Education, 2019, 17 (6): 1 173-1 193.

[18] 吴增生．数学抽象的认知与脑机制[J]．数学教育学报，2018，27（4）：68-75．

[19] SIMON M A, KARA M, PLACA N, et al. Towards an integrated theory of mathematics conceptual learning and instructional design: The learning through activity theoretical framework [J]. Journal of Mathematical Behavior, 2018, 52: 95-112.

[20] BICER A, LEE Y, PERIHAN C, et al. Considering mathematical creative self-efficacy with problem posing as a measure of mathematical creativity [J]. Educational Studies in Mathematics, 2020, 105 (3): 457-485.

[21] SCHOEVERS E M, KROESBERGEN E H, MOERBEEK M, et al. The relation between creativity and students’ performance on different types of geometrical problems in elementary education [J]. ZDM, 2022, 54 (1): 133-147.

[22] MOLAD O, LEVENSON E S, LEVY S. Individual and group mathematical creativity among post-high school students [J]. Educational Studies in Mathematics, 2020, 104 (2): 201-220.

[23] LU X L, KAISER G. Can mathematical modelling work as a creativity-demanding activity? An empirical study in China [J]. ZDM, 2022, 54 (1): 67-81.

[24] GUO Y F, YAN J J, MEN T Y. Chinese junior high school students’ mathematical problem-posing performance [J]. ZDM, 2021, 53 (4): 905-917.

[25] BAUMANNS L, ROTT B. The process of problem posing: Development of a descriptive phase model of problem posing [J]. Educational Studies in Mathematics, 2022, 110 (2): 251-269.

[26] CAI J F, HWANG S. Teachers as redesigners of curriculum to teach mathematics through problem posing: Conceptualization and initial findings of a problem-posing [J]. ZDM, 2021, 53 (6): 1 403-1 416.

[27] HARTMANN L M, KRAWITZ J, SCHUKAJLOW S. Create your own problem! When given descriptions of real-world situations, do students pose and solve modelling problems? [J]. ZDM, 2021, 53 (4): 919-935.

[28] GUO M, LEUNG F K S, HU X. Affective determinants of mathematical problem posing: The case of Chinese Miao students [J]. Educational Studies in Mathematics, 2020, 105 (3): 367-387.

[29] CANTORAL R, MORENO-DURAZO A, CABALLERO-PÉREZ M. Socio-epistemological research on mathematical modelling: An empirical approach to teaching and learning [J]. ZDM, 2018, 50 (1/2): 77-89.

[30] YANG X R, SCHWARZ B, LEUNG I K C. Pre-service mathematics teachers’ professional modeling competencies: A comparative study between Germany and China [J]. Educational Studies in Mathematics, 2022, 109 (2): 409-429.

[31] ASEMPAPA R S, BROOKS G P. Factor analysis and psychometric evaluation of the mathematical modeling attitude scale for teachers of mathematics [J]. Journal of Mathematics Teacher Education, 2022, 25 (2): 131-161.

[32] OREY D C, ROSA M. Developing a mathematical modelling course in a virtual learning environment [J]. ZDM, 2018, 50 (1/2): 173-185.

[33] KRAWITZ J, CHANG Y P, YANG K L, et al. The role of reading comprehension in mathematical modelling: Improving the construction of a real-world model and interest in Germany and China [J]. Educational Studies in Mathematics, 2022, 109 (2): 337-359.

[34] DE VETTEN A, SCHOONENBOOM J, KEIJZER R, et al. Pre-service primary school teachers’ knowledge of informal statistical inference [J]. Journal of Mathematics Teacher Education, 2019, 22 (6): 639-661.

[35] AYAN R, ISIKSAL-BOSTAN M. Middle school students’ proportional reasoning in real life contexts in the domain of geometry and measurement [J]. International Journal of Mathematical Education in Science and Technology, 2019, 50 (1): 65-81.

[36] MKHATSHWA T P. Calculus students’ quantitative reasoning in the context of solving related rates of change problems [J]. Mathematical Thinking and Learning, 2020, 22 (2): 139-161.

[37] INGLIS M, FOSTER C. Five decades of mathematics education research [J]. Journal for Research in Mathematics Education, 2018, 49 (4): 462-500.

[38] SCHOENFELD A H. Research in mathematics education [J]. Review of Research in Education, 2016, 40 (1): 497-528.

[39] STROHMAIER A R, SCHIEPE-TISKA A, CHANG Y P, et al. Comparing eye movements during mathematical word problem solving in Chinese and German [J]. ZDM, 2020, 52 (1): 45-58.

[40] PLATH J, LEISS D. The impact of linguistic complexity on the solution of mathematical modelling tasks [J]. ZDM, 2018, 50 (1/2): 159-171.

[41] LUTOVAC S, KAASILA R. Methodological landscape in research on teacher identity in mathematics education: A review [J]. ZDM, 2019, 51 (3): 505-515.

[42] WILLIS R, LYNCH D, PEDDELL L, et al. Development of a teacher of mathematics identity (ToMI) scale [J/OL]. Mathematics Education Research Journal, https://doi.org/10.1007/s13394-021-00391-w.

[43] CRIBBS J, HAZARI Z, SONNERT G, et al. College students’ mathematics-related career intentions and high school mathematics pedagogy through the lens of identity [J]. Mathematics Education Research Journal, 2021, 33 (3): 541-568.

[44] LOUIE N, ADIREDJA A P, JESSUP N. Teacher noticing from a sociopolitical perspective: The FAIR framework for anti-deficit noticing [J]. ZDM, 2021, 53 (1): 95-107.

[45] KÖNIG J, SANTAGATA R, SCHEINER T, et al. Teacher noticing: A systematic literature review of conceptualizations, research designs, and findings on learning to notice [J]. Educational Research Review, 2022, 36: 100 453.

[46] ALWAST A, VORHÖLTER K. Measuring pre-service teachers’ noticing competencies within a mathematical modeling context-an analysis of an instrument [J]. Educational Studies in Mathematics, 2022, 109 (2): 263-285.

[47] BERGSTEN C, FREJD P. Preparing pre-service mathematics teachers for STEM education: An analysis of lesson proposals [J]. ZDM, 2019, 51 (6): 941-953.

[48] CHEN C S, LIN J W. A practical action research study of the impact of maker-centered STEM-PjBL on a rural middle school in Taiwan [J]. International Journal of Science and Mathematics Education, 2019, 17 (Z): 85-108.

[49] MAASS K, GEIGER V, ARIZA M R, et al. The role of mathematics in interdisciplinary STEM education [J]. ZDM, 2019, 51 (6): 869-884.

[50] SWIDAN O, FRIED M. Focuses of awareness in the process of learning the fundamental theorem of calculus with digital technologies [J]. Journal of Mathematical Behavior, 2021, 62: 100 847.

[51] COLLINS B V C. Flipping the precalculus classroom [J]. International Journal of Mathematical Education in Science and Technology, 2019, 50 (5): 728-746.

[52] GHEDAMSI I, LECORRE T. Transition from high school to university calculus: A study of connection [J]. ZDM, 2021, 53 (3): 563-575.

[53] 朱琳，蒋启芬．国外线性代数的教学研究述评[J]．数学教育学报，2018，27（1）：79-84．

[54] OKTAÇ A. Mental constructions in linear algebra [J]. ZDM, 2019, 51 (7): 1 043-1 054.

[55] HOCH S, REINHOLD F, WERNER B, et al. Design and research potential of interactive textbooks: The case of fractions [J]. ZDM, 2018, 50 (5): 839-848.

[56] FAN L H, CHENG J, XIE S C, et al. Are textbooks facilitators or barriers for teachers’ teaching and instructional change? An investigation of secondary mathematics teachers in Shanghai, China [J]. ZDM, 2021, 53 (6): 1 313-1 330.

[57] JIA S, YAO Y. 70 Years of problem posing in Chinese primary mathematics textbooks [J]. ZDM, 2021, 53 (4): 951-960.

[58] HOHENSEE C. Preparing elementary prospective teachers to teach early algebra [J]. Journal of Mathematics Teacher Education, 2017, 20 (3): 231-257.

[59] XIE S Y, CAI J F. Fifth graders’ learning to solve equations: The impact of early arithmetic strategies [J]. ZDM, 2022, 54 (6): 1 169-1 179.

[60] BLANTON M, STEPHENS A, KNUTH E, et al. The development of children’s algebraic thinking: The impact of a comprehensive early algebra intervention in third grade [J]. Journal for Research in Mathematics Education, 2015, 46 (1): 39-87.

[61] PRAETORIUS A K, CHARALAMBOUS C Y. Classroom observation frameworks for studying instructional quality: Looking back and looking forward [J]. ZDM, 2018, 50 (3): 535-553.

[62] BLÖMEKE S, KAISER G, KÖNIG J, et al. Profiles of mathematics teachers’ competence and their relation to instructional quality [J]. ZDM, 2020, 52 (2): 329-342.

[63] FRANCIS D C, EKER A, LIU J Q, et al. (Mis) alignment between noticing and instructional quality: The role of psychological and cognitive constructs [J]. Journal of Mathematics Teacher Education, 2022, 25 (5): 599-632.

[64] 董连春，吴立宝，王立东．PISA2021数学素养测评框架评介[J]．数学教育学报，2019，28（4）：6-11，60．

[65] DI MARTINO P, GREGORIO F, IANNONE P. The transition from school to university in mathematics education research: New trends and ideas from a systematic literature review [J]. Educational Studies in Mathematics, 2023, 113 (1): 7-34.

[66] HANNULA M S. International trends in mathematics education research [C] // LEPIK M. Teaching mathematics: Retrospective and perspectives. Tallinn: Tallinn University, 2009: 11-18.

[67] GÖKÇE S, GÜNER P. Forty years of mathematics education: 1980—2019 [J]. International Journal of Education in Mathematics Science and Technology, 2021, 9 (3): 514-539.

[68] 陈昊，王建磐．21世纪国际数学教育在关注什么——基于ICME中TSG主题的分析[J]．数学教育学报，2020，29（2）：41-48．

[69] The International Program Committee for ICME-15. Topic study groups [EB/OL]. (2023-02-20) [2023-03-10]. https://icme15.com/program/topic-study-groups.

[70] 谢圣英，喻平．基础教育中的文化意识批判[J]．教育研究与实验，2012（1）：46-50．

[71] 杨启亮．教师培养的国际视野和本土化实践[J]．教育发展研究，2010，30（24）：1-6．

[72] 侯文，朱琳琳．关于数学教学效率评价的实证研究[J]．数学教育学报，2010，19（3）：35-38．

[73] CAI J F, MORRIS A, HOHENSEE C, et al. Reconceptualizing the roles of researchers and teachers to bring research closer to teaching [J]. Journal for Research in Mathematics Education, 2018, 49 (5): 514-520.

Knowledge Base and Frontiers of International Mathematics Education Research——A Bibliometric Analysis about International Journals in Mathematics Education from 2018 to 2022

ZHENG Guo-qiang, XIE Sheng-ying

(School of Mathematics and Statistics, LHPCSIP (MOE), Hunan Normal University, Hunan Changsha 410081, China)

The number of annual publications in the field of international mathematics education has shown an overall upward trend. The results of a bibliometric analysis of the literature revealed that: based on the knowledge base provided by methodological books, educational policy documents, research handbooks, and critical literature, the frontiers of international mathematics education research focus on “mathematical processes”, “mathematical contents”, “mathematical teaching and learning environments” and “mathematics teacher education”. The research examines mathematical cognition, ability, and competency around the PISA mathematics framework; has established critical links among mathematical learning at the primary, secondary, and tertiary levels; focuses on the environmental aspects of mathematical teaching and learning in the context of sociocultural differences; and has maintained “mathematics teacher education” as a frontier of research since the 21st century. In the field of mathematics education in China, we should enhance critical cultural awareness to assess the frontiers of international mathematics education research, conduct localization research in mathematics education, and strengthen the communication between education research and practice.

mathematics education research; knowledge base; international research frontier; localization research; bibliometric analysis

G420

A

1004–9894（2024）01–0089–09

郑国强，谢圣英．国际数学教育研究的知识基础与前沿——基于2018—2022年数学教育国际期刊的文献计量分析[J]．数学教育学报，2024，33（1）：89-97．

2023–12–27

湖南省哲学社会科学基金一般项目——中学教师数学英才教育观研究（21YBA039）

郑国强（1999—），男，湖南祁阳人，硕士生，主要从事数学课程与教学论研究．谢圣英为本文通讯作者．

[责任编校：陈汉君、陈隽]