不同控制策略下直驱风电机组的机网耦合特性及稳定性分析

饶仪明，吕 敬，戴金水，王 晗，蔡 旭

（电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市 200240）

0 引言

直驱全功率风电机组是风力发电机的主流机型之一,尤其在海上风电中占主导地位［1］。然而,直驱风电机组与弱交流电网［2］、串补网络［3］、柔性直流输电系统［4-5］等交/直流电网间的动态交互易引发宽频振荡现象,近年来引起了工业界和学术界的广泛关注。

直驱风电机组通过全功率背靠背变流器接入电网,包含机侧变流器和网侧变流器。机、网侧变流器多采用传统矢量控制策略,机侧变流器通过控制永磁同步发电机的输出功率实现最大功率跟踪,网侧变流器控制直流母线电压恒定［6］。早期研究普遍认为,直驱风电机组的机、网侧变流器通过直流母线电容解耦,其并网特性主要由网侧变流器决定。因此,研究中通常忽略机侧系统（包括发电机和机侧变流器）动态,将机侧系统简化为一个理想功率源［7-9］。然而,文献［10-11］定性分析了机侧系统动态对直驱风电机组交流侧阻抗特性的影响,指出忽略机侧系统动态可能会导致并网稳定性的误判。文献［12］定量分析了直驱风电机组机网耦合特性及其关键影响因素,揭示了机侧系统动态对直驱风电机组并网稳定性的影响机制。在传统矢量控制外,文献［13］提出了一种增强直驱风电机组电网故障穿越能力的新型双闭环矢量控制策略,该控制策略通过机侧变流器控制直流母线电压,通过网侧变流器控制有功功率。文献［14］对比研究了直驱风电机组在该新型矢量控制策略和传统矢量控制策略下的直流侧动态及其关键影响因素,指出当直流母线电压由机侧变流器控制时,直流侧动态的阻尼较弱,但并没有分析两种控制策略下直驱风电机组的机网耦合特性及并网稳定性。

近年来,随着风电接入比例的不断提高,具有电网主动支撑能力的构网型风电机组成为研究热点［15］。为使并网逆变器模拟同步发电机的运行特性,文献［16］依据同步发电机的转子运动方程提出了虚拟同步机（virtual synchronous generator,VSG）控制策略,使并网逆变器具备功率同步特性；文献［17］则依据并网逆变器和同步发电机在结构和特性上的对偶关系,提出了并网逆变器的惯性自同步控制（inertia synchronization control,ISynC）策略,利用直流母线电容的惯性实现同步并网。基于上述并网逆变器的两种典型构网型控制,提出了两种主流的构网型直驱风电机组控制策略:1）机侧变流器采用矢量控制方案控制直流母线电压,网侧变流器采用VSG 控制实现功率同步并网［18］,即VSG 型直驱风电机组；2）机侧变流器采用矢量控制方案控制有功功率或其相关量（如电磁转矩）实现最大功率跟踪,网侧变流器采用直流电容惯性同步控制实现惯性同步并网［19］,即ISynC 型直驱风电机组。在构网型直驱风电机组的小信号稳定性分析方面,文献［20］利用阻抗法研究了VSG 型直驱风电机组并弱电网的稳定性,指出VSG 型直驱风电机组交流侧阻抗在基频以下的容性特性可能导致其接入感性弱电网时产生失稳风险；文献［21］采用特征值分析法研究了VSG 型直驱风电机组的并网稳定性,指出VSG 型直驱风电机组具有较好的弱电网适应性,但在强电网下容易出现低频振荡问题；文献［19］分析了ISynC 型直驱风电机组接入弱电网的稳定性,指出附加惯量传递控制环节会降低ISynC 型直驱风电机组弱电网运行稳定性。然而,上述文献没有讨论构网型直驱风电机组的机网耦合特性,对不同构网型控制策略下机侧系统动态对直驱风电机组并网特性的影响尚不明确。

综上所述,现有研究仅对传统矢量控制策略下直驱风电机组的机网耦合特性进行了深入分析,但对其他典型控制策略下直驱风电机组的机网耦合特性及其关键影响因素尚不明确。此外,现有文献尚缺乏针对不同控制策略下直驱风电机组统一形式的宽频阻抗建模方法,尤其是尚无文献建立ISynC 型直驱风电机组的阻抗模型。为此,本文针对直驱风电机组机网耦合特性开展深入研究,建立4 种典型控制策略下直驱风电机组统一形式的交流侧宽频阻抗模型,并进行扫频验证；基于解析阻抗模型和机网耦合度指标对不同控制策略下直驱风电机组的机网耦合特性及其关键影响因素进行对比分析；以直驱风电机组并弱交流电网为分析案例,验证不同控制策略下机网耦合特性对直驱风电机组并网稳定性分析的影响。

1 不同控制策略下直驱风电机组的阻抗模型

1.1 直驱风电机组的主电路及控制结构

图1 为直驱风电机组的主电路结构及4 种典型控制策略的控制框图。图中:s为拉普拉斯算子；PLL 表示锁相环；MPPT 表示最大功率点跟踪；SVPWM 表示空间矢量脉宽调制；PMSG 表示永磁同步发电机；Vmabc和Imabc分别为机侧变流器交流侧三相电压和电流；Cdc为直流母线电容；Vdc为直流母线电压；Vabc和Iabc分别为网侧变流器交流侧三相电压和电流；Viabc为经过电感滤波器后的三相交流电压；Lf和Rf分别为电感滤波器的等效电感和电阻；ωm为永磁同步发电机的转速；θm和θe分别为转子的机械角度和电角度；np为永磁同步发电机的极对数；Imd和Imq分别为Imabc经过Park 变换得到的机侧变流器交流侧电流的d、q轴分量；Vmd,ref和Vmq,ref分别为机侧变流器控制器输出的电压调制信号d、q轴分量；Vmabc,ref为Vmd,ref和Vmq,ref经过反Park 变换得到的机侧变流器三相电压调制信号；dmabc为机侧变流器的开关信号；P和Q分别为直驱风电机组输出的有功功率和无功功率；θ为网侧变流器控制器Park 变换所使用的同步旋转角度；Id和Iq分别为Iabc经过Park 变换得到的网侧变流器交流侧电流的d、q轴分量；Vid和Viq分别为Viabc经过Park 变换得到的d、q轴分量；Vd,ref和Vq,ref分别为网侧变流器控制器输出的电压调制信号d、q轴分量；Vabc,ref为Vd,ref和Vq,ref经过反Park 变换得到的网侧变流器三相电压调制信号；dabc为网侧变流器的开关信号；Te为永磁同步发电机的电磁转矩,Te,ref为其给定值；Imd,ref和Imq,ref分别为机侧变流器交流侧电流参考值的d、q轴分量；ωe和Lm分别为永磁同步发电机的转子电角速度和绕组电感；ψr为磁链；ω0为基频对应的角频率；Id,ref和Iq,ref分别为网侧变流器交流侧电流参考值的d、q轴分量；Vdc,ref和Qref分别为直流电压和无功功率的给定值；HT(s)、Hmc（s）、Hdc(s)、HQ（s）、Hc（s）分别为电磁转矩控制器、机侧电流控制器、直流电压控制器、无功功率控制器和网侧电流控制器的传递函数；HPQ（s）为网侧变流器功率外环控制器的传递函数；Pref为有功功率的给定值；J为虚拟惯量；K为无功控制系数；Dp为频率下垂系数；Dq为电压下垂系数；Vt,ref为反电动势电压幅值的给定值；Vd为Vabc经过Park 变换得到的d轴分量；ω为有功控制环生成的同步角速度；Vdc,Base为直流电压基准值；ωBase为网侧变流器输出电压角频率的基准值；Vd,Base为网侧变流器交流侧d轴电压的基准值；Vt,Base为反电动势电压幅值的基准值；SBase为直驱风电机组的额定容量。

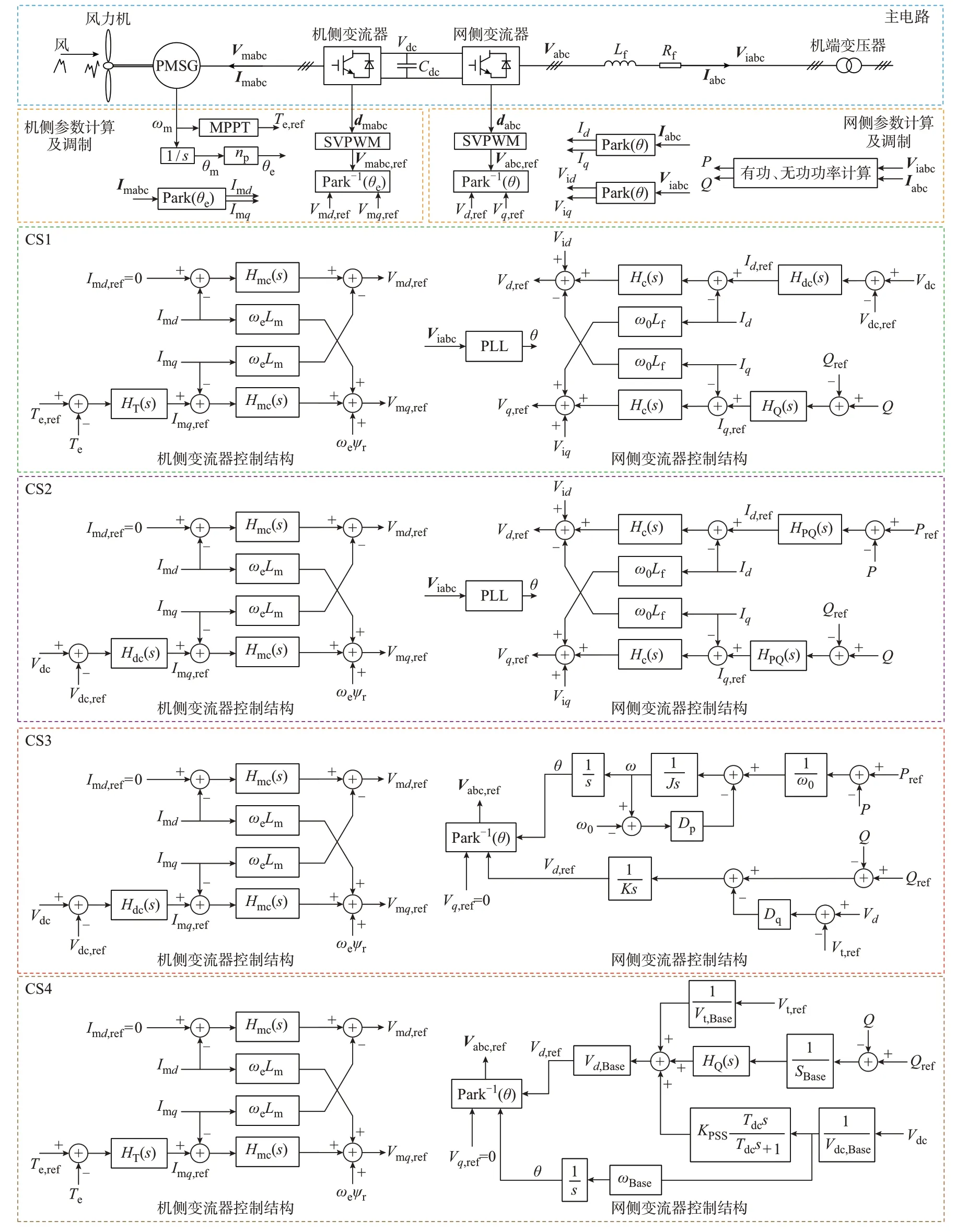
图1 直驱风电机组主电路及4 种控制策略结构示意图Fig.1 Schematic diagram of main circuit and four types of control strategies of direct-drive wind turbines

直驱风电机组的主电路结构及应用最为广泛的双闭环矢量控制策略——控制策略1（CS1）在文献［12］中得到了详细阐述,不再赘述。

对直驱风电机组的另外3 种典型控制策略描述如下:

控制策略2（CS2）［13］:机侧和网侧变流器均采用双闭环矢量控制,但与CS1 不同的是,CS2 机侧变流器控制直流母线电压,网侧变流器控制有功功率。

控制策略3（CS3）［18］:机侧变流器控制直流母线电压,其控制结构与CS2 的机侧控制完全一致,但网侧变流器采用VSG 控制。VSG 控制无需PLL,而是利用有功控制环和无功控制环分别生成同步旋转角度θ和d轴调制电压Vd,ref。

控 制 策 略4（CS4）［19］:机 侧 变 流 器 控 制 有 功 功率,其控制结构与CS1 的机侧控制完全一致,但网侧变流器采用ISynC 控制。在ISynC 控制中,直流电压标幺值被用作网侧变流器输出电压角频率的标幺值,进而经过积分器生成同步旋转角度θ。直驱风电机组输出的无功功率Q可通过调整调制电压的幅值来调节。此外,ISynC 控制还采用了包含高通滤波器（Tdc为高通滤波时间常数）和致稳控制系数KPSS的附加稳定控制回路来增加系统阻尼。

当调制方式为补偿调制时,直驱风电机组机/网侧系统解耦,采用直接调制是探讨直驱风电机组机网耦合特性的前提条件［12］。因此,本文工作建立在变流器采用直接调制的基础上。

1.2 直驱风电机组的通用小信号阻抗建模方法

基于直驱风电机组的模块化多端口小信号模型,可以推导得到直驱风电机组交流端口阻抗的通用求解表达式,从而将不同控制策略下直驱风电机组的阻抗模型纳入统一架构。

直驱风电机组的模块化多端口小信号模型在文献［12］中已有详细阐述,此处不再赘述。基于直驱风电机组的模块化多端口小信号模型,可以推导得到直驱风电机组机侧系统等效至直流端口的小信号导纳YdcMSS,进而推导得到直驱风电机组整体交流端口dq阻抗Zac,即

式中:“Δ”表示相应变量的小信号分量；上标“s”表示电气系统坐标系中相应变量；Imdc为机侧变流器直流侧电流,以流入机侧变流器为正；ZPMSG为永磁同步发电机的小信号dq阻抗矩阵；Ymdq为机侧变流器的交流侧自导纳矩阵,主要由机侧变流器的控制系统决定；Ya和Yb为机侧变流器的交直流侧耦合导纳矩阵；Ymdc为机侧变流器的直流侧自导纳；Ydq为网侧变流器的交流侧自导纳矩阵,主要由网侧变流器的控制系统决定；Yc和Yd为网侧变流器的交直流侧耦合导纳矩阵,Ydc为网侧变流器的直流侧自导纳。

值得注意的是,当推 导得到Ymdq、Ya、Ydq和Yc的详细表达式后,可分别根据机、网侧变流器的交直流侧功率守恒推导得到Yb、Ymdc、Yd和Ydc的详细表达式,具体计算方法见文献［12］。

根据式（1）和式（2）,直驱风电机组的交流侧小信号阻抗模型可通过推导关键参数矩阵Ymdq、Ya、Ydq、Yc的详细表达式来建立。在直驱风电机组的阻抗模型中,控制策略的不同体现为关键参数矩阵的详细表达式不同。为区分不同控制策略下的关键参数矩阵,本文为相应矩阵名称附加控制策略编号,例如Ya2表示CS2 的Ya。

值得说明的是,在机侧变流器控制直流母线电压时（如CS2 和CS3）,忽略机侧系统动态的直驱风电机组交流侧阻抗即为网侧变流器的交流侧自阻抗,即有Zac,sim=(Ydq)-1。对于通过机侧变流器控制实现MPPT 的CS1 和CS4,忽略机侧系统动态即意味着将机侧系统简化为恒功率源。因此,CS1 或CS4 控制下忽略机侧系统动态的直驱风电机组交流侧阻抗可由式（2）改写得到,即

式中:Vdc0为直流母线电压的稳态值。

上文所得阻抗为dq阻抗模型,可根据文献［22］将所建立的dq阻抗模型进一步转化为单输入-单输出正序阻抗模型。

下文在阐述不同控制策略下直驱风电机组的阻抗模型时,仅展示关键参数矩阵具体表达式的关键推导过程。

1.3 4 种控制策略下直驱风电机组的小信号阻抗模型

由于采用CS1 的直驱风电机组的小信号阻抗模型在文献［12］中已得到详细阐述,本文在附录A式（A1）中直接给出了CS1 下关键参数矩阵的详细表达式。下文分别介绍CS2、CS3 和CS4 下关键参数矩阵的推导过程。

由于变流器控制中的解耦项对直驱风电机组正序阻抗的影响较小［23］,本文在阻抗建模过程中省略了解耦项。

1）CS2

CS2 的控制结构与CS1 类似,仅在外环控制量上存在差别。因此,CS2 下的关键参数矩阵推导过程与CS1 一致。由于篇幅限制,本文仅给出CS2 下机侧变流器和网侧变流器的外环控制方程（式（4）和式（5））以及关键参数矩阵的详细表达式（式（6））。

式中:I为单位矩阵；参数矩阵A2、B2的详细表达式见附录A 式（A2）。

2）CS3

由于CS3 的机侧变流器控制结构与CS2 完全一致,有:

VSG 控制下网侧变流器的有功控制环、无功控制环的控制方程可分别表示为:

将式（8）进行小信号线性化,并考虑直接调制过程和控制系统坐标系与电气系统坐标系之间的转换关系,可以推导得到:

式中:参数矩阵F3、G3的详细表达式见附录A式（A3）。

3）CS4

由于CS4 的机侧变流器控制结构与CS1 完全一致,有:

ISynC 控制下网侧变流器的控制方程为:

将式（11）进行小信号线性化,并考虑直接调制过程和控制系统坐标系与电气系统坐标系之间的转换关系,可以推导得到:

式中:Zdqf为交流滤波器的小信号dq阻抗矩阵；参数矩 阵Ts和Tv的 详 细 表 达 式 见 附 录A 式（A3）,A4、B4、C4的详细表达式见式（A4）。

1.4 阻抗模型验证

为验证所建立阻抗模型的准确性,在MATLAB/Simulink 中分别搭建采用上述4 种控制策略的直驱风电机组时域仿真模型,主要参数见附录B 表B1。其中,主电路参数来源于实际工程中的直驱风电机组,4 种控制策略的控制参数则是根据文献［19,24-25］中的控制参数整定方法设计得到。

对于每一种控制策略下的直驱风电机组仿真模型,在交流侧依次注入频率在1～1 000 Hz 范围内的扰动电压信号（1～200 Hz 的频率间隔为1 Hz,201～1 001 Hz 的频率间隔为25 Hz）,测量对应频率下的扰动电流响应,进而可计算得到直驱风电机组在对应频率下的交流侧小信号阻抗［26］。直驱风电机组交流侧小信号阻抗扫频测量的具体步骤如附录B 图B1 所示。

通过上述方法可获得4 种控制策略下直驱风电机组的宽频阻抗（扫频测量阻抗,即阻抗的真实值）,基于所建立的阻抗模型可以计算得到4 种控制策略下直驱风电机组的理论计算阻抗,将扫频测量阻抗与理论计算阻抗进行对比,结果如图2 所示。可以看到,直驱风电机组在4 种控制策略下的理论计算阻抗与扫频测量阻抗具有很好的一致性,验证了所建立宽频阻抗模型的准确性。

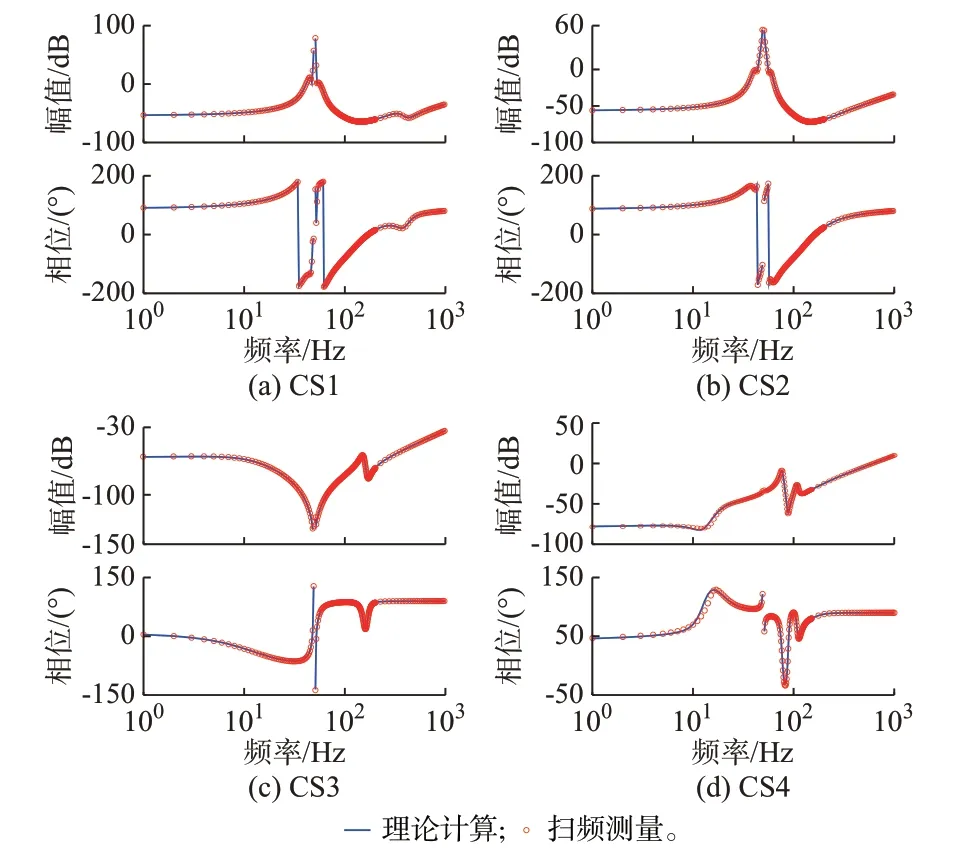
图2 不同控制策略下直驱风电机组阻抗模型验证Fig.2 Impedance model validation of direct-drive wind turbines with different control strategies

2 不同控制策略下直驱风电机组机网耦合特性分析

2.1 机侧系统动态总体影响的对比分析

图3 展示了不同控制策略下是否考虑机侧系统动态对直驱风电机组交流侧阻抗特性的影响。4 种控制策略下的直驱风电机组主电路参数完全一致。控制参数选取方法如下:对于4 种控制策略中的双闭环矢量控制,按照相同或相似控制环节（例如均是电流内环或均是电流外环）的闭环带宽保持一致的原则来确定控制器比例-积分（PI）参数（基本计算方法见文献［24］）。具体地,机/网侧电流内环带宽被设置为200 Hz,直流电压/转矩/功率外环带宽被设置为10 Hz,PLL 带宽被设置为30 Hz；对于VSG 控制和惯性同步型控制,采用典型的电压源控制参数设计方法设计相应参数［19,25］。对比考虑机侧系统动态的直驱风电机组详细阻抗特性和忽略机侧系统动态的简化阻抗特性,可以反映机侧系统动态的总体影响。

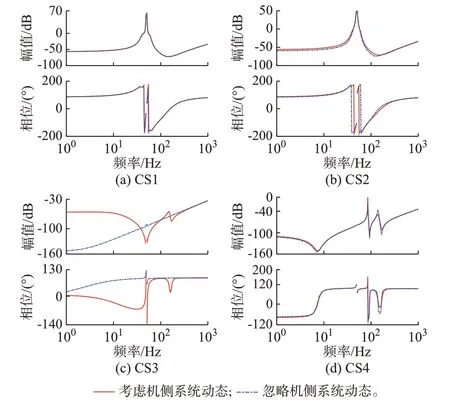
图3 不同控制策略下直驱风电机组阻抗特性Fig.3 Impedance characteristics of direct-drive wind turbines with different control strategies

从图3（a）可以看到,在CS1 下,红色实线与蓝色虚线几乎完全重合,说明在CS1 下直驱风电机组的阻抗特性受其机侧系统动态影响较小,即直驱风电机组机网耦合程度较低。然而,如图3（b）所示,当直驱风电机组采用CS2 时,是否计及机侧系统动态对直驱风电机组的交流侧阻抗特性存在较为明显的影响。如图3（c）所示,在CS3 下,忽略机侧系统动态的简化阻抗特性与考虑机侧系统动态的详细阻抗特性在中低频段（200 Hz 以下）完全不同:当忽略机侧系统动态时,直驱风电机组的阻抗特性在全频段内近似感性特性；当考虑机侧系统动态时,直驱风电机组的阻抗在次同步频段内呈现容性特性。如图3（d）所示,采用CS4 的直驱风电机组交流侧阻抗特性受机侧系统动态的影响较小,与采用CS1 的直驱风电机组较为类似,说明在该控制策略下忽略机侧系统动态不会对直驱风电机组的交流侧阻抗模型精度产生较大影响。

因此,相较于采用CS1 或CS4,采用CS2 或CS3时直驱风电机组的机网耦合程度较高,意味着机侧系统动态对直驱风电机组交流侧中低频段阻抗特性具有较大影响。

2.2 机网耦合特性的量化分析

为量化分析不同控制策略下直驱风电机组的机网耦合特性,定义机网耦合度λc,如式（13）所示。

式中:Zcom和Zsim分别为考虑和忽略机侧系统动态的直驱风电机组交流侧阻抗；f为频率。

式（13）的物理含义为忽略机侧系统动态对直驱风电机组交流侧阻抗模型造成的相对误差。因此,较高的耦合度说明直驱风电机组机网耦合效应较为显著。研究发现,电网强度的变化不影响直驱风电机组在不同控制策略下机网耦合度的相对大小规律。因此,仅展示理想电网条件下采用不同控制策略的直驱风电机组的机网耦合度,结果如图4 所示。可以看到,在大部分频段内采用CS2 或CS3 时直驱风电机组的机网耦合度高于CS1 或CS4。

图4 不同控制策略下直驱风电机组机网耦合度比较Fig.4 Comparison of generator-grid coupling degrees of direct-drive wind turbines with different control strategies

值得注意的是,CS2 和CS3 均是机侧变流器控制直流母线电压,而CS1 和CS4 均是网侧变流器控制直流母线电压。因此,可以得出如下结论:当机侧变流器控制直流母线电压时,直驱风电机组的机网耦合效应将会加剧,此时忽略机侧系统动态会对直驱风电机组交流侧阻抗模型的精度造成较大误差。

图4 所示为典型控制参数下不同控制策略直驱风电机组机网耦合度的比较。为说明本文研究结论具有普适性,对每一种控制方式,考虑各控制参数的不同取值,在各种参数组合下绘制直驱风电机组机网耦合度曲线,结果如附录C 图C1 所示。分析结果表明,即使在不同控制参数下,各控制策略的机网耦合度仍满足上述结论,本文的研究结论具有较好的普适性。

不同控制策略下控制参数和直流母线电容对直驱风电机组机网耦合度的影响分析详见附录C。

3 案例研究

本章利用阻抗稳定性分析方法分析4 种控制策略下直驱风电机组并弱交流电网的稳定性。对于每一种控制策略,分别采用考虑机侧系统动态的详细阻抗模型和忽略机侧系统动态的简化阻抗模型来分析互联系统的（潜在）振荡频率和稳定裕度,以验证机网耦合特性对直驱风电机组并网系统稳定性分析的影响。图5 展示了稳定性分析结果,其中,交流电网的短路比为3,直驱风电机组在4 种控制策略下均输出1 MW 有功功率和0.1 Mvar 无功功率。由于交流电网等效阻抗的相位为90°,根据阻抗稳定性分析理论,当直驱风电机组与电网阻抗幅值曲线相交频率处的直驱风电机组阻抗相位小于-90°时,互联系统将失稳,失稳域如图5 所示。

图5 不同控制策略下直驱风电机组并网稳定性分析Fig.5 Analysis of grid-connected stability for directdrive wind turbines with different control strategies

由图5 可以得出以下结论:

1）如图5（a）所示,在CS1 下,无论是否考虑机侧系统动态,互联系统稳定性分析结果都落在失稳域内,且分析得到的振荡频率和相位裕度非常接近。具体地,当忽略机侧系统动态时,分析得到的振荡频率和相位裕度分别为84 Hz 和-4.8°；当考虑机侧系统动态时,分析得到的振荡频率和相位裕度分别为83.8 Hz 和-4.5°。因此,对于采用CS1 的直驱风电机组,忽略机侧系统动态对其并网稳定性分析结果的影响较小。

2）如图5（b）所示,在CS2 下,当考虑机侧系统动态时,互联系统稳定性分析结果落在失稳域外,相位裕度为2.9°,表明系统稳定；而当忽略机侧系统动态时,互联系统稳定性分析结果落在失稳域内,系统稳定裕度被误判为-4.5°,表明系统失稳。因此,对于采用CS2 的直驱风电机组,忽略机侧系统动态对其并网稳定性分析结果的准确性影响较大。

3）如图5（c）所示,在CS3 下,考虑机侧系统动态的详细阻抗与忽略机侧系统动态的简化阻抗在中低频段（如200 Hz 以下）存在较大差异。考虑机侧系统动态的直驱风电机组详细阻抗与交流电网阻抗的幅频曲线在17.9 Hz 处相交,相位裕度为37.7°；忽略机侧系统动态的直驱风电机组简化阻抗与交流电网的阻抗幅频曲线不存在任何交点,可视为相位裕度无穷大。虽然无论考虑机侧系统动态与否对采用CS3 的直驱风电机组并网系统进行稳定性分析都能够得出系统稳定的结论,但是所得到的系统稳定裕度的分析结果存在较大差别。需要说明的是,当采用CS3 的直驱风电机组接入柔性直流输电系统时,由于柔性直流输电系统在次同步频段可能存在感性负电阻特性,可能与直驱风电机组在次同步频段的容性特性相互作用,产生振荡风险。然而,在CS3下,忽略机侧系统动态的直驱风电机组阻抗在全频段内均是感性,无法反映该场景下的振荡风险。因此,对于采用CS3 的直驱风电机组,忽略机侧系统动态对其并网稳定性分析结果的影响较大。

4）如图5（d）所示,在CS4 下,无论考虑机侧系统动态与否,互联系统稳定性分析结果都落在失稳域外,表明系统稳定,且分析得到的振荡频率和相位裕度较为接近,与CS1 的情况类似。因此,对于采用CS4 的直驱风电机组,机网耦合效应对其并网稳定性分析结果的影响较小。

图6 展示了相应的时域仿真结果,其中,交流电网的初始短路比为4,当仿真进行10 s 时,将交流电网的短路比降低至3。从图中可以看出,当采用CS1 时,直驱风电机组在电网短路比降低至3 后发生振荡现象,公共耦合点（point of common coupling,PCC）的电流IPCC迅速畸变,与上文忽略/考虑机侧系统动态的稳定性分析结果一致；当采用CS2 时,直驱风电机组在电网短路比降低至3 后仍然能够保持稳定,与前文考虑机侧系统的稳定性分析结果一致,验证了在CS2 下忽略机侧系统动态会导致系统稳定性误判的结论；当采用CS3 或CS4时,直驱风电机组在电网短路比降低至3 后均保持稳定,验证了上文忽略/考虑机侧系统动态的稳定性分析结果的准确性。

图6 不同控制策略下直驱风电机组并网电流波形Fig.6 Grid-connected current waveforms of direct-drive wind turbines with different control strategies

另一方面,为对比不同控制策略下直驱风电机组的弱电网运行能力,在仿真第20 s 时,进一步将交流电网的短路比降低至2。对比不同控制策略下的仿真结果可以看到,当电网短路比降低至2 后,采用CS1 的直驱风电机组并网点电流由之前的等幅振荡迅速发散,系统崩溃；采用CS2 的直驱风电机组也迅速失稳导致系统崩溃；而两种电压源型控制（CS3和CS4）的直驱风电机组则能在短路比为2 的极弱电网条件下继续保持稳定运行,具有更好的弱电网运行能力。此外,对比CS1 和CS2 可知,机侧变流器控制直流母线电压的矢量控制策略可在一定程度上改善直驱风电机组的并网稳定性。

4 结语

本文建立了4 种典型控制策略下直驱风电机组的精细化宽频阻抗模型,对比研究了不同控制策略下直驱风电机组的机网耦合特性,以及是否考虑机侧系统动态对其并网稳定性分析精度的影响。结论如下:

1）当网侧变流器控制直流母线电压（如传统矢量控制、ISynC 型直驱风电机组等）时,直驱风电机组的机网耦合程度较低,忽略机侧系统动态对其并网稳定性分析精度的影响较小。

2）当机侧变流器控制直流母线电压（如VSG 型直驱风电机组等）时,直驱风电机组的机网耦合程度较高,机侧系统动态对直驱风电机组交流侧阻抗特性影响较大（主要体现在中低频段）。特别地,当网侧变流器采用VSG 控制时,机网耦合尤为显著。在此类控制策略下,忽略机侧系统动态可能会对直驱风电机组并网稳定性分析带来较大误差。

3）矢量控制策略下（如CS1 和CS2）,机侧或网侧变流器的控制参数以及直流母线电容值对机网耦合度具有较大影响；而电压源控制策略下（如CS3和CS4）,机侧或网侧变流器控制参数对机网耦合度影响较小,且直流母线电容值主要影响中高频段的机网耦合特性。

4）机侧变流器控制直流母线电压的矢量控制策略可在一定程度上改善直驱风电机组的并网稳定性；相较于采用电流源型控制的直驱风电机组,电压源型控制的直驱风电机组具有更好的弱电网运行能力。

本文研究结论可为不同控制策略下直驱风电机组的建模与分析提供参考。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。