基于SVR和随机森林模型的动力煤高位发热量预测研究

郭龙，郭文文

（1.浙江浙能富兴燃料有限公司，浙江 杭州 310023;2.浙江科技学院机械与能源工程学院，浙江 杭州 310023）

0 引 言

近年来，全球能源短缺问题日益严重，燃煤电厂仍将在我国的电力供应领域发挥基础作用。2021年，中国燃煤发电量创下历史新高，增长了8%，满足了一半以上的电力需求[1]。结合超低排放和碳捕获利用与储存（CCUS）技术[2]，燃煤电厂仍将提供更加低碳和环保的电力[3]。在煤炭贸易领域，发热量是作为煤炭交易定价不可或缺的指标。高位发热量（HHV）是动力煤最具代表性的特征之一，该定义是给定质量的煤炭在标况下完全燃烧时释放的热量。煤的HHV由绝热或等温氧弹量热仪系统测定反应物和产物之间的焓变化来计算[4]。

自杜龙公式以来，有许多研究尝试通过易获取的煤炭指标来预测煤炭发热量。然而，大多数相关研究基于对特定种类煤炭的元素分析数据得出，由于煤阶和岩相成分各不相同，杜龙公式只能准确预测有限的发热量范围。Hosokai等人[5]对杜龙公式进行了修正，对406种具有识别结构的标准气态有机化合物的发热量进行了预测。Singh和Kakati[6]基于来自160个印度煤炭样本的数据集，建立了C/H/O原子比率与HHV之间的关系模型，获得的平均误差在0.9%以内。Neavel等人[7]提出了一个基于66个北美煤源煤样的经验公式，这些相同产地煤的平均绝对误差达0.45%。Channiwala和Parikh[8]开发了一个统一的模型，根据元素组成预测固体、液体和气体燃料的高位发热量，提供1.45%的平均绝对误差。Parikh等人[9]基于工业分析，建立了相关性模型来预测煤炭发热量，得到的平均绝对误差为3.74%。Majumder等人[10]从印度煤的工业分析成分中获得了HHV模型：灰分、水分、挥发份和固定碳。该模型在预测特定印度煤炭样本集方面具有较低的平均绝对误差，约1.46%。Komilis等人[11]根据工业和元素分析数据建立了固体废物发热量模型并评估了模型的性能，获得了0.852的决定系数。

传统的线性模型可以揭示HHV与工业分析和元素分析数据的联系。然而，由于不同地区煤的岩相结构不尽相同，很难获得适用于各种煤的通用模型。为了提高预测模型的准确性和泛化能力，研究人员在煤HHV建模过程中采用了新型的统计学习方法。大多数统计学习模型都是非线性模型，对大量特定输入数据具有更好的拟合能力和预测精度。Tan等人[12]基于两个单独的中国和美国煤炭数据集构建了一个支持向量回归（SVR）模型。中国和美国煤炭HHV的平均绝对误差分别为2.16%和2.42%。Yi等人[13]提出了一系列相关性模型来预测煤炭成分，使用最小二乘回归（LR）的广义方法，对不同等级的煤炭进行建模分析。Ghosh等人[14]采用人工神经网络算法（ANN）根据印度煤田原煤检测数据训练多层网络，并进一步使用预测的发热量对该煤田的煤层进行分级。

考虑到工业分析相对于元素分析的易获得性，本研究的主要目的是利用两种不同的统计学习算法（SVR和随机森林）建立回归模型，并评估它们在揭示中国典型动力煤HHV与工业分析关系的能力。目前还没有关于随机森林模型预测国内动力煤高位发热量HHV的研究报道。在许多已发表的研究中，输入数据集是从不同测量精度、不同测试环境、不同来源收集的。数据收集中的不一致会对模型精度造成一定影响。而在本工作中，数据集是从5700个煤炭样本的统一标准测量中获取。对采用SVR和随机森林法的模型进行了详细构建和测试，以评估其性能。

1 建模方法

1.1 支持向量回归（SVR）方法

支持向量机（SVM）首先由Cortes和Vapnik提出[15]，基于双组分类的 SVM，将输入向量非线性映射到高维特征空间。为了扩大SVM的应用范围，Boser等人[16]提出了核技巧的概念，Drucker等人[17]改进了回归问题中的算法。SVR的基本思想是找到一个分离的超平面，在数据点之间创建边界。SVR 模型中的分离超平面必须正确分离具有最大几何边距的数据集，分离超平面不仅可以很好地处理高确定性的训练数据，还可以很好地处理未知数据。如图 1所示，考虑到非线性映射函数ϕ(x)很难直接获取，输入向量空间可以通过核技巧K(x,z)=ϕ(x)·ϕ(z)隐式转换为更高维空间。支持向量是距边距边界内分离超平面距离最近的样本。该模型是通过用±ε(称为ε管)惩罚分离超平面区域之外的偏差来训练模型。给定Xi的训练向量，回归问题可以转换为以下最小化问题：

约束条件：

式中：C是限制区间ε之外向量的惩罚系数。

图1 支持向量回归求解框架图

ξi和ξi*是引入的松弛变量，以允许每个训练向量的松弛大于ε。表示来自训练数据的经验风险。w和b分别是超平面的法向量和截距。

为了求解上述方程描述的原始优化问题，引入了拉格朗日乘子向量αi=(α1,α2,...,αN)T≥0。拉格朗日函数可以按如下方式获得：

在Karush-Kuhn-Tucker条件下，可表示为：

求解上述对偶问题，可以得到SVR预测函数：

其中α*表示对偶问题的解，w* 和b* 表示原始问题的解。K(xi,xj)是核函数[18]。K(xi,xj)作为SVR的关键，使模型能够求解非线性问题。SVR 模型中使用的内核函数表示如下：

线性核函数：

多项式核函数：

高斯核函数(RBF)：

Sigmoid 核函数：

式中：γ、r和p是描述内核函数的相应参数。调查中使用的参数描述和值空间显示在表 1 中。LSVR、PSVR、RSVR 和 SSVR 表示具有不同内核函数的 SVR 模型：即线性 SVR、多项式SVR、RBF SVR 和 sigmoid SVR。

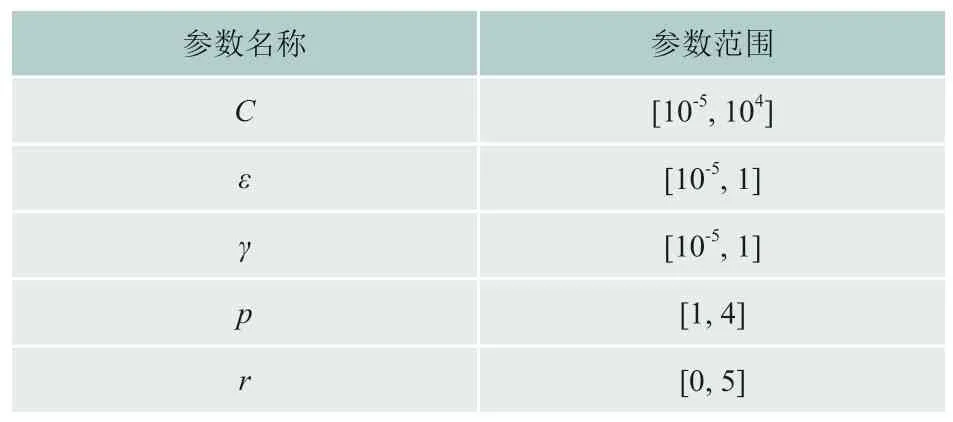
表1 SVR模型参数描述

1.2 随机森林模型

随机森林是由Breiman等人[19]开发的一种集成统计学习技术，作为CART算法（分类和回归树算法）[20]的改进。与传统的决策树算法和神经网络算法相比，RF回归具有计算资源相对较少、预测精度更高的优势。RF模型被认为在处理分类和回归问题时具有较高的鲁棒性和抗过拟合性，因为它可以调用数千棵CART树[21]。

随机森林回归算法被视为一组回归树的集合。图2显示了RF模型预测的构建框架。如图 2所示，一个回归树表示一组规则，这些规则可以从根节点连续应用于输入数据的叶节点。随机选择一组输入变量，并从原始数据集中替换以形成回归树。每棵树都根据选择分割变量 j 和平方误差最小的分割点 s 的标准进行分割：

图2 基于随机森林的煤炭高位发热量构建框架

其中y表示数据集的输出变量。R1和R2是根据分裂变量j和分裂点s定义的两个区域：

重复以上分割过程，直到树停止生长。得到回归树模型的解是：

其中I(x∈Ri)i是索引函数：

通过组合这些树并对每棵树的预测求平均值，可以获得最终预测值。

1.3 模型验证与评估

为了确定HHV预测模型参数，采用holdout交叉验证和五折交叉验证方法相结合。将工业分析和HHV测量实验的数据集随机分为训练集和测试集。训练集占整个数据集的65%，测试集占35%。随后，将训练集随机分为5个大小相同的互不相交子集。五个子集中的一个被选为验证集，选择过程重复五次，并计算总平均误差。

使用以下统计指标评估SVR和RF模型。平均绝对误差MAE和均方误差的计算公式[22]为：

一些国有企业会计人员职业道德意识薄弱，不能够遵守职业规范，不能坚持原则，在利益的驱动下、在外部的压力下采用伪造、变造、篡改、毁损会计资料，编制虚假会计账簿、会计报表等，帮助企业、帮助经营者向外提供虚假的会计信息和经济指标。

其中ti是测量的 HHV，yi是相应模型的预测HHV。

为了比较不同模型之间的百分比误差，研究中还使用了平均绝对百分比误差（MAPE）：

在交叉验证和网格搜索过程中，决定系数（R2）也用于评估模型预测的准确性：

2 结果和讨论

2.1 工业分析和HHV测定结果

为了了解工业分析和HHV范围，数据集的数据分布显示在图3中：灰分(Ad)含量为4.17%～36.48%，挥发份(Vd)含量为21.84%～42.35%，固定碳(FCd)含量为37.41%～66.95%，HHVd为20.74 MJ/kg～31.02 MJ/kg。

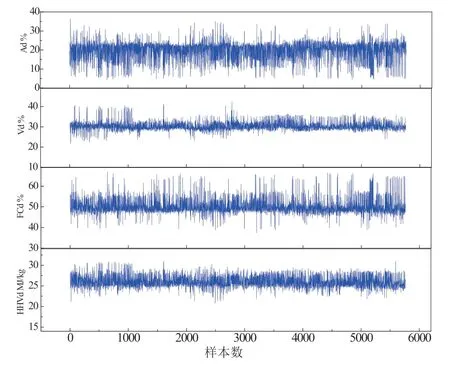
图3 工业分析及高位发热量实测数据集分布图

挥发份是动力煤重要的燃用指标之一。由于测量方便，在中国煤分类标准GB/T5751中，干燥无灰基挥发分(即Vdaf)与黏结指数和胶质层最大厚度等其他参数一起作为煤等级的主要指标[23]。工业分析结果的分布显示，数据集中的动力煤的Vd含量主要集中在28%～34%的范围内(Vdaf33%～40%)，表明大多数被测煤样品具有相似的煤炭分类。数据集中的动力煤主要为不粘煤和长焰煤，其灰分和固定碳含量的波动范围相对较大。很明显，灰分和固定碳(FC)含量对煤样的高位发热量都有显著影响。较低的灰分和较高的固定碳含量代表较高的HHV。然而，HHV与工业分析数据之间的更深层次关联还与煤等级及其他物理化学特性密切相关。

2.2 预测高位发热量的性能评价

表2显示了用于预测高位发热量的SVR和RF模型的整体性能。对于测试数据集，所有构建模型的MAPE值都小于1.5%。决定系数是识别模型准确性的最常用指标之一。用于测试数据集的 R2值越大通常意味着更好的预测能力。在所有五种模型预测结果中，RF模型均表现出最佳性能，MAPE为0.96%，R2为0.943。同时，RSVR在4种SVR模型中表现出最佳的HHV预测能力，MAPE为0.97%，R2为0.943。

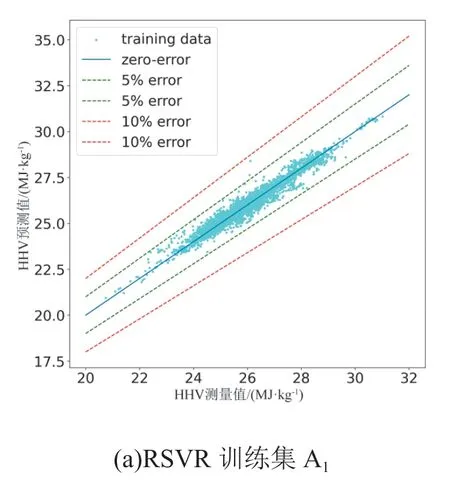
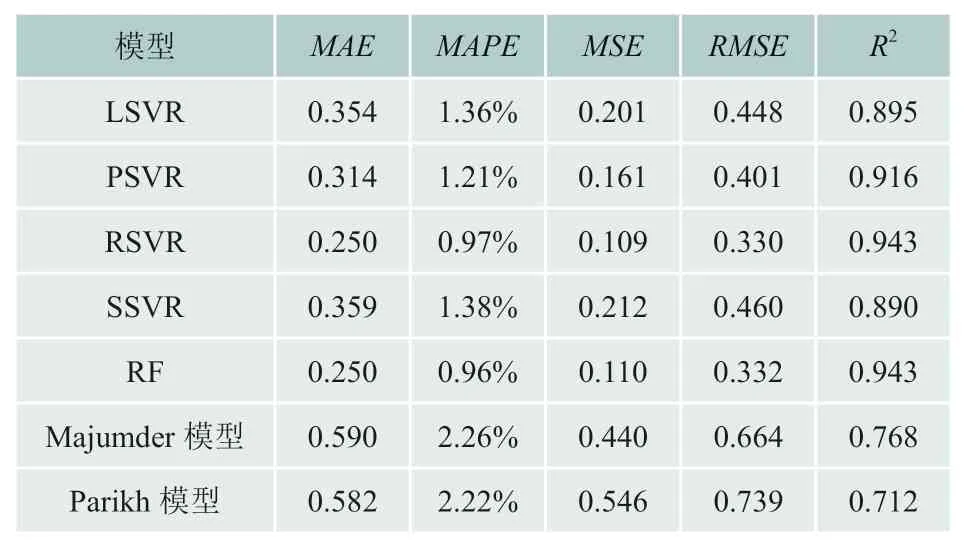
表2 SVR及RF模型高位发热量预测结果统计分析

RSVR和RF模型的估计结果如图4所示。蓝色实线表示每个HHV预测的零误差，而绿色和红色虚线分别标识5% 和10% 的误差线。从图4可以明显看出，估计结果与测量数据一致，训练和测试数据的估计结果紧密分布在零误差线周围，几乎所有数据点都位于所有模型和数据集的10% 误差线范围内。

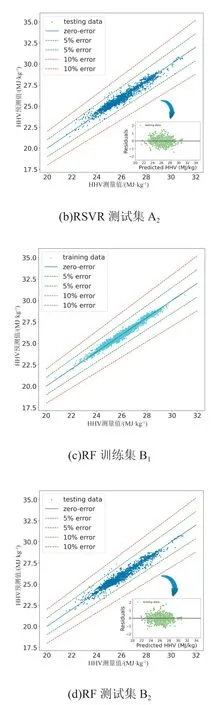
图4 不同模型动力煤高位发热量预测结果误差图

对于RF模型的预测结果，测试数据点分布在零误差线周围的狭窄区域，这意味着它能够更好地预测工业分析与HHV结果之间的关系。为进一步体现模型的预测能力，在测试数据误差图右下角绘制了测试集数据的残差图。在26.00～28.00 MJ/kg 的HHVd范围内，残差图在零误差线周围显示出更好的随机性，这意味着该范围内的模型可以描述有关煤炭 HHV 的大部分可预测信息。在两侧范围内，残差图围绕零误差线不对称，表明这些范围内的预测能力相对较差，这可能是由于该范围内煤样的数据不完整和理化特征差异造成的。

2.3 与其他预测方法的比较

如表2所示，将LSVR、PSVR、RSVR、SSVR和RF模型的性能估计与Majumder[10]和Parikh[9]提出的预测方法进行了比较。由于工业分析数据不能反映煤HHV的所有影响因素，因此HHV与工业分析结果的相关性通常对燃料来源具有更高的精度。为了进一步提高Majumder和Parikh腐蚀对中国煤炭的预测精度，Tan等人[12]修正了与中国煤炭数据集的相关性参数，提高了预测能力。改进后的Majumder和Parikh列示如下：

修正后的Majumder和Parikh的5700个国内煤炭数据的MAPE分别为2.26%和2.22%，比RSVR和RF模型高出约2.5倍；相比之下，RSVR和RF模型的R2要高得多，表明这两种模型具有更出色的高位发热量预测能力。

2.4 不同类型动力煤的进一步验证

从上述性能估计来看，给定动力煤数据集，RSVR和RF模型仅通过给定工业分析数据即可较准确地预测HHV，特别是在HHVd26.00～28.00 MJ/kg和28%～34% Vd（对应Vdaf33%～40%）附近。

在ISO 11760标准：煤的分类[24]中，煤的分类方法基于三种煤特性：平均随机镜质组反射率以划分煤阶，无矿物质基镜质体含量以表征煤炭岩相组成，以及灰分产量以表征煤中无机物含量，通过综合指标可以精确地描述煤的理化性质。然而，在工业应用中，Vdaf是对煤进行分类的更加快速便捷的指标[22]。图5显示了中国煤炭测得的HHV百分比绝对误差（来自Tan等人[12]的数据）与SVR和RF模型的预测之间的百分比绝对误差的比较。值得注意的是，RSVR和RF模型在Vdaf范围内的绝对误差百分比都非常低，为28%～42%。在10%～28%（主要是贫煤和焦煤）和42%～58%的范围内，该模型的绝对误差要高得多。RF模型对各类煤的适应性和稳定性优于RSVR模型，在Vdaf=28%～42%范围预测误差曲线较低，这可能由于大规模训练数据减少了测量中的偶然误差，并尽可能地提高了预测的准确性。

图5 SVR和RF模型对国内煤炭高位发热量预测值与测量值误差对比

选取澳大利亚、印度等其他地区煤源的动力煤，验证了该模型的可用性和适用范围。澳大利亚、印度煤炭样本数据来自Aich等人[25]（图6）。结果还表明，RF模型在预测动力煤的HHV方面表现出色(Vdaf=33%～40%)。

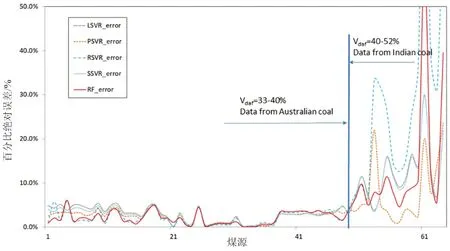
图6 SVR和RF模型对澳大利亚和印度煤炭高位发热量预测值与测量值误差对比

3 结论

本研究对5700份动力煤样品进行了工业分析和高位发热量测定试验，探讨了两者之间的关系。基于实验数据集，构建并利用5种模型（LSVR、PSVR、RSVR、SSVR和RF）寻找最优超参数和预测模型。此外，还结合不同煤源的煤炭高位发热量预测情况进行了比较分析，并进一步验证了所建立模型的高位发热量预测性能，得出以下结论：

1)从预测结果来看，RSVR和RF模型利用动力煤的数据集可以准确预测HHV，特别是在HHVd范围为26.00～28.00 MJ/kg，Vd范围为28%～34%（对应Vdaf33%～40%）。RSVR和RF模型在测试数据集中的平均百分比误差分别为0.97%和0.96%。

2)所构建的模型在预测动力煤的HHV方面均表现良好（Vdaf= 33%～40%）。在无烟煤（Vdaf=0～10%）、褐煤（Vdaf=42%～60%）和贫瘦煤、焦煤（Vdaf=10%～28%）范围内，SVR和RF模型的绝对误差相对较高。

3)通过绝对百分比误差比较，可以看出RF模型总体上比SVR模型表现出更好的适应性和稳定性，表明随机森林法在预测动力煤高位发热量方面具有广阔的应用前景。