基于粗糙分析的大学英语考试质量提升路径

柳媛慧,陈林书,赵肄江,彭理,梁伟

(湖南科技大学 1.外国语学院;2.计算机科学与工程学院,湖南 湘潭 411201)

在世界经济、文化趋于一体化的形势下,英语教育对大学生的重要性不言而喻,而检验大学英语教育教学质量和效果的最有效手段就是组织英语考试。大学英语考试是考查学生知识掌握情况、衡量教学效果、保证教学质量的重要手段,也是调整和改进教师教学工作,控制和激发学生学习行为的重要依据[1-2]。大学英语考试试题质量的高低直接影响考试的可靠度和准确度,进而直接或间接地影响学生的学习态度和学习行为。因此,提升大学英语考试试题质量是至关重要的一个研究课题。

传统的大学英语考试试题质量提升路径有数理统计法,即对试卷的平均分、标准差、可信度、覆盖率、有效性、区分度以及优秀率、及格率和不及格率等指标进行统计和分析[3-5],进而对考试试题进行增删调整和质量提升。其中:可信度衡量试题的可靠性与稳定性,覆盖度表显示知识覆盖面的大小和程度,有效性表示考试实际结果与预期目标的差距,标准差反映分数的离散分布情况,区分度体现不同水平学生对同一类考试题的区分和鉴别能力。

然而,长期的大量实践数据表明,上述传统的数理统计方法仅能够指导调整大学英语考试试题的难易程度、知识覆盖面、有效性等,即只就卷面上的显著问题进行简单的统计、分析、评价和质量提升,不能深度挖掘试卷结构是否合理、试题内容与教学大纲是否一致,特别是不能智能判断试题的冗余性(是否重复)、重要性程度(是否是教学重点)等信息[6]。

粗糙集理论[7]由波兰数学家Pawlak提出,具有成熟的数学基础,不需要先验知识,避免了知识主观评价带来的误差,其主要思想是在保持信息系统分类能力不变的前提下,通过知识约简导出问题的分类或决策规则[8]。粗糙集理论是一种处理不精确、不一致、不完备信息的有效工具,直接对数据本身进行分析和推理,从中发现隐含的知识,揭示潜在的规律,它是一种天然的数据挖掘或者知识发现方法。粗糙集理论已广泛应用于预测与控制、图像处理、故障诊断、模式识别与分类、机器学习和数据挖掘等领域。

数理统计方法一般需要根据专家知识库提供的主观经验值,如标准差、可信度和覆盖率等统计指标,容易出现主观评价带来的误差[9-10]。粗糙集理论正好能够弥补数理统计方法的这一缺陷,它具有成熟的数学基础,不需要任何主观性的先验知识,完全根据已有知识库进行分析,挖掘潜在的隐含知识和规则,具有客观性和价值性[11-13]。

本文借助粗糙集理论这一经典数学分析工具,研究大学英语考试质量提升路径。下面借助粗糙集的决策表、相对正域、冗余属性和属性重要度基本概念,提出试题冗余性的定性判别方法和试题重要度的定量度量方法,建立基于粗糙分析的大学英语考试质量提升模型。大量实验分析验证了新方法的有效性,即新型方法发现并修正了部分冗余的和重要度较低的试题,有效提高了试卷命题质量,对指导大学英语教学工作、提高教学质量具有重要指导意义。

1 方法建模

本节先给出粗糙集中决策表和相对正域的形式化定义及其简要描述,再根据粗糙集中相对正域和属性重要性概念定义大学英语考试试题冗余性判别方法和试题重要度度量方法。

定义1(决策表)称四元组K=(U,S,V,f)是一个信息系统或知识库,简单记为K=(U,S)。其中:论域U是对象的有限集合,属性S是非空有限集合,属性值域V=∪a∈AVa,Va表示属性a∈A的值域,信息函数f:U×A→V是一个映射。进一步地,称K为一个决策表,若满足S中属性,可划分为两个不相交的子集——条件属性C和决策属性D,其中,S=C∪D且C∩D≠φ,记为K=(U,C∪D)。特别地,称K为一个单决策表,若满足D={d},记为K=(U,C∪{d})。

决策表是粗糙集理论中的一类特殊且非常重要的信息系统,多数决策问题在具体应用中都可以用决策表来解决。在实际应用中,通常用一张二维表表示信息系统。其中:行表示研究对象,列表示对象属性,属性值表示对象信息,一个或多个列属性对应一个等价关系,一个二维表对应一族等价关系。

定义2(相对正域)给定决策表K=(U,C∪D),r⊆C,X⊆U则称posC(D)为C相对于D的正域,其中,posC(D)如下:

(1)

相对正域posC(D)表示U中所有可以根据分类U/C的信息准确划分到关系D的等价关系中去的对象集合。相对正域是粗糙集理论中一个非常重要的概念,它是属性集C相对决策D的分类能力的强度描述。

1.1 试题冗余性判别方法

在大学英语考试中,可以将一个试题看作一个条件属性r,将所有讨论的目标试题看作条件属性集C,并将所有目标试题的总分看作决策属性D,那么,由目标试题和总分构成的成绩表就是一个决策表,且是一个单决策表。于是,可以用如下方法定义试题冗余性。

定义3(试题冗余性)在给定决策表K=(U,C∪D)和试题r⊆C,若相对正域posC-{r}(D)=posC(D),则称r为C相对D的不必要属性,简称r为冗余属性,否则称r为C相对D的必要属性。

上述定义中,给定大学英语考试试卷成绩对应的决策表K=(U,C∪D)中,试题r⊆C,相对正域posC(D)表示试题集C相对总分D的分类能力描述。于是,我们可以用如下方法分析试题r是否冗余:若从试题集C中去掉试题r之后,剩余试题集C-{r}对决策D的分类能力没有变化,则说明试题r是冗余的,是不必要的,是可以删除的。

1.2 试题重要度度量方法

在大学英语考试试卷题型的成绩表构成的决策表K=(U,C∪D)中,根据定义3试题冗余性的判别方法:若试题r是冗余属性,则r的重要度为0,可以直接删除,没有继续讨论其试题重要度的意义了;否则,试题r是必要的。那么,接下来的问题是:试题r有多重要?如何对其进行定量、定义和度量呢?

于是,根据粗糙集理论中属性重要度的概念,可以用如下方法定量度量试题r的重要度:试题r⊆C,根据定义1中相对正域posC(D)的概念,可以用两个相对正域中元素个数之差来定量描述试题r的重要性程度,即利用定义4关于属性重要度的计算公式来定量度量试题重要性。

定义4(试题重要度)给定大学英语考试试卷成绩对应的决策表K=(U,C∪D),试题r∈C,则称sig(r,C,D)为试题r相对于试题集C相对总分D的重要性程度,简称“r的试题重要度”。其中,|U|为学生集合U的基数,sig(r,C,D)如下:

(2)

上述定义中,若r是非必要的,则它的重要度显然为0。但若属性r是必要的,则可以用试题重要度来定量试题r的重要性。显然,有sig(r,C,D)≥0,且:其值越大,r的重要度就越大;其值越小,r的重要度就越小。

2 实验分析

首先,详细交代实验驱动、实验目标、实验数据离散化方法、实验数据类型和实验数据来源等内容;接着,以粗糙集的冗余属性和属性重要度为依据,提出大学生英语考试试题冗余性的定性判别方法;然后,给出大学生英语考试试题重要度的定量度量方法;最后,通过计算194名大学生的大学英语考试试题的冗余性和重要度,发现并修正了部分冗余的和重要度低的试题,有效提高了大学英语考试命题质量。

2.1 数据准备

大学英语考试试卷中,试题是基本元素,试卷的质量由所有试题的质量共同决定。整套试卷中,每一小题是否科学合理,是否满足大纲要求,是否客观反映学生的实际水平,对整套试卷的质量起着决定性作用。

在试卷中,有时会存在以下情况:两道题目所考的内容相同或者相似,学生会做其中一道题,就会做另一道题,我们称另一道题目是不必要的,冗余的,可以删除的。有时还会存在另一种情况,且这种情况较常出现:某一题目比较容易,绝大多数学生都能够回答正确,仅有极少数学生不能拿到分数,这说明这一试题重要度低,测试意义不大,应该对其进行替换或者难度调整。

但是,在考试之前,试题的冗余性和重要度很难由命题老师主观给出,因为学生的基础水平和学习情况参差不齐,命题老师既担心考试题目太难导致学生考试不及格,又担心考试太容易测试不出学生的真实水平。

本实验不需要期望值和覆盖标准等任何参考值。教师不在考试之前主观评价或提升试卷质量,而是在考试之后通过学生考试成绩反过来分析试题的冗余性和重要度,对冗余的或者重要度低的试题进行删减和质量提升,从而提高试卷的整体质量。

在下面的实验中,需要对大学英语考试的原始成绩进行离散化处理。按照学校的一般性处理方法,将学生考试的百分制成绩离散化为A(优秀,90～100分)、B(良好,80～89分)、C(中等,70～79分)、D(及格,60～69分)和E(不及格,60分以下)五个成绩等级,如表1所示。

表1 百分制分数与离散后成绩等级的对应关系

为便于分析题目的冗余性和重要度,需要进一步将每一道题目的得分离散化。例如:题目c1满分为12分,某学生实际得分为8分,换算百分制为8÷12×100≈66.7分,则此学生题目c1的得分等级为D。按此方法,某学生的部分考试题目得分及离散化的成绩等级如表1所示。其中:题目编号后括号内的数值表示该题目的总分数,如c1(8)表示题目c1的满分为8分;“/”前后分别表示得分和对应的得分等级,如“8/A”表示题目c1得了8分,离散化的成绩等级为A。

本次实验的试卷样本为湖南科技大学2021-22-2学期非英语专业大二英语期末考试试卷,考试题型有听力题、阅读理解题、翻译题和写作题(共55个题目计100分):Listening部分共23题计30分,其中题目1～16每题1分,题目17～23每题2分;Reading部分共30题计40分,其中题目24～33每题2分,题目34～53每题1分;Translation(Chinese to English)部分共1题计15分;Writing部分共1题计15分。题型构成如表2所示。

表2 大学英语考试试卷的题型构成

本次实验的成绩样本为湖南科技大学2021级电子信息工程1～3班、能源化学工程2班、测控技术与仪器1班、车辆工程1班、机械电子工程1～2班、土木工程1～3班、工程管理2班共194名学生的考试原始成绩,其中男生126人,女生68人。

2.2 实验过程

下面根据定义3中试题冗余性判别方法分析样本试题的冗余性。

为了让讨论简单方便且不失一般性,随机从试卷中抽取10名学生6道题目的考试分数作为样本,试题原始成绩如表3所示。再按表1中的方法离散化,得到对应分数等级的决策表,如表4所示。

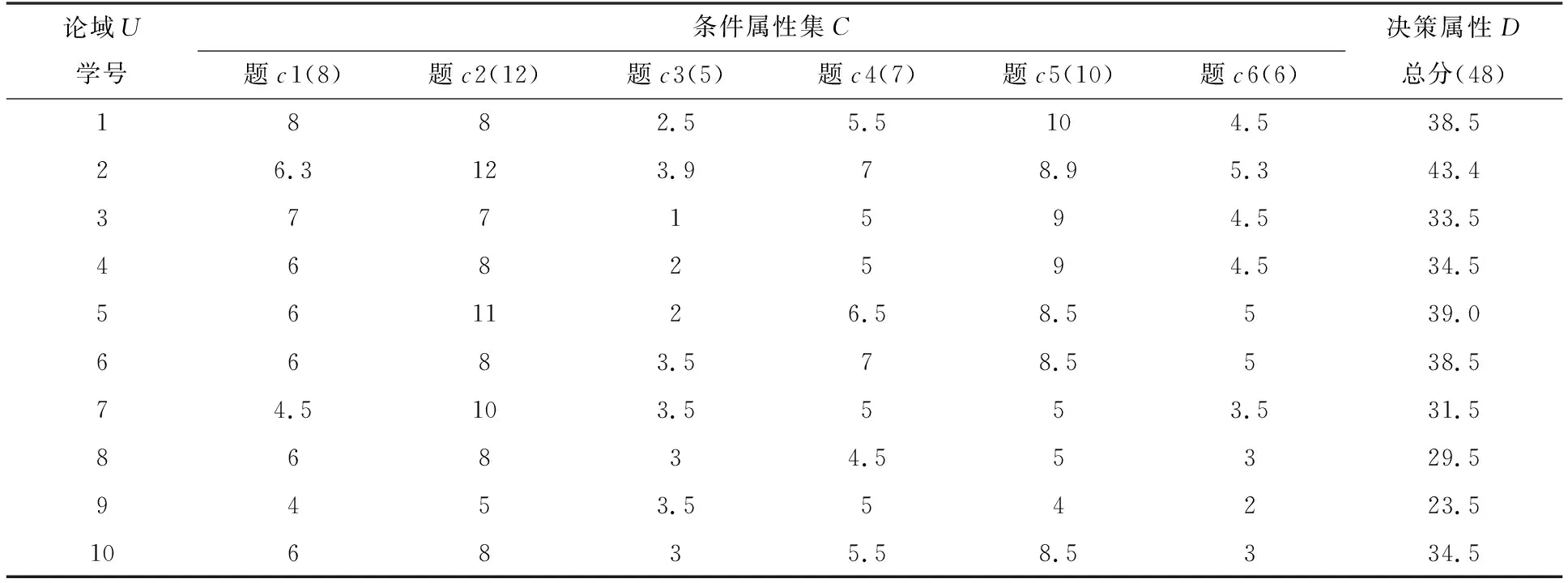
表3 学生部分试题原始成绩 (单位:分)

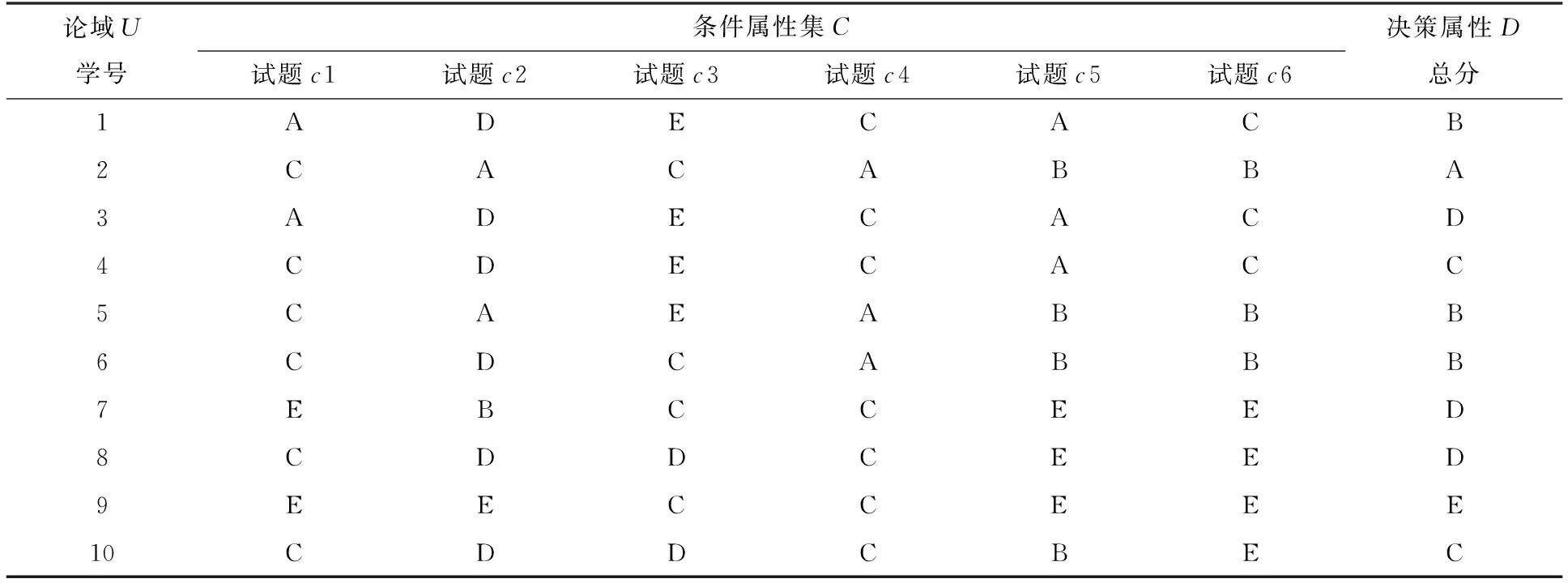
表4 学生部分试题原始成绩离散化后的决策

将表4中的试题集{c1,c2,c3,c4,c5,c6}看作条件属性C,总分看作决策属性D,则表4是一个典型的决策表。利用定义3中冗余属性的判别方法,可以分别判别试题{c1,c2,c3,c4,c5,c6}是否为不必要属性,即是否是冗余的,可以删除的。

根据表4容易求得决策属性D、条件属性集C和条件属性集C-{c4}的等价类分别是:

再根据定义2,可分别求得条件属性C和条件属性C-{c4}相对决策属性D的正域:posC(D)={2,4,5,6,7,8,9,10},posC-{c4}(D)={2,4,5,6,7,8,9,10}。

显然,有posC-{c4}(D)=posC(D),则由定义3关于冗余属性的判别方法可知,题目c4对总分D的分类能力不产生影响,是一个不必要属性,是冗余的,可以删除的。

同理,c6也是一个不必要属性,是冗余的,可以删除的。

但是,同理可求得,题目c1、c2、c3和c5是必要属性,不可以删除。

由上文可知,题目c4和c6是不必要属性,说明对样本学生1～10和样本题目c1～c6来说,c4和c6对总分D的信息量划分并没有减少,即c4和c6是不必要的,是冗余的,可以删除的,不太科学合理的。

下面根据定义4中试题重要度的判别方法分析样本试题重要度。

为了让讨论简单方便且不失一般性,随机从样本中抽取8名学生的Listening、Reading、Translation和Writing等4个题型的考试分数作为样本,原始成绩如表5所示。再按表1中的方法离散化,得到对应分数等级的决策表,如表6所示。

表5 学生各题型的原始成绩 (单位:分)

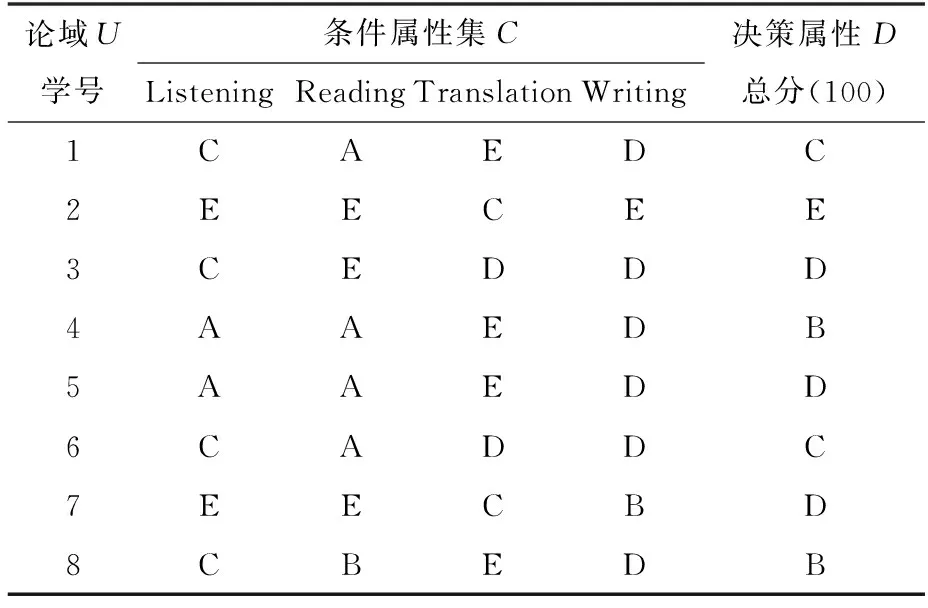
表6 学生各题型原始成绩离散化后的决策

根据表6容易求得决策属性D(总分)、条件属性集C和C-{Listening}的等价类分别是:

根据定义2,可分别求得条件属性C和C-{Listening}的相对正域:

posC(D)={1,2,3,6,7,8},posC-{Listening}(D)={2,3,6,7,8}。

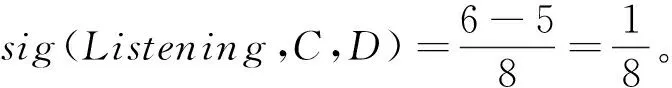
同理,可分别求得条件属性Reading、Translation和Writing的属性重要度:

从上述条件重要性的求解结果可知,显然有sig(Reading,C,D)>sig(Writing,C,D)

>sig(Listening,C,D)=sig(Translation,C,D)。这说明,在大学英语考试中,Reading部分最重要,对总成绩的影响最大,其重要度远远高于其他部分;其次是Writing部分;相比之下,听力与翻译的重要度最低。

2.3 结果分析

本次实验的数据总量和计算工作量相当大。因此,实验采用经典粗糙集数据分析工具集Rosetta 2.0,它具有数据导入、导出、补全、离散化、知识约简、过滤、分类规则生成、等价类和上下近似集获取等功能。实验通过Rosetta 2.0软件对194名大学生的成绩进行了离散、等价类获取、相对正域和属性重要度求解等预处理和计算。

实验需要将考生的试题离散化为A、B、C、D和E五个等级。但是,本次英语考试试卷的题目中1～33都是单项选择题(即客观题),要么是满分(A级),要么是零分(E级),这意味着客观题都是布尔类型数据,显然不能将试题得分离散化为A、B、C、D和E五个等级。因此,需要在实验中将多个单项选择题组合成一个题目,如将选择题1、2和3组合成题目c1。

在判别试题冗余性的实验中,通过对194名大学生的42个组合题目进行统计分析,我们发现其中的两组组合题目——题目3、11、30和题目19、27是冗余的,说明这些题目是不太科学合理的,需要对其进行修改和质量提升。

在定量度量试题重要度的实验中,先对194名大学生的Listening、Reading、Translation和Writing共4个组合题目(题型)的试题重要度进行分析,得出的结论与2.2节的实验结果基本一致,也与各题型的分值比例基本保持一致,其中,Reading、Listening、Writing和Translation部分的重要度占比分别为64.5%、24.8%、14.6%和14.1%,如图1所示。这说明在大学英语考试命题中,应该将重点放在Reading部分,其次是Listening部分。相比较而言,Writing和Translation部分的重要性最低,且重要度基本相同,这与大学英语的教学目标和考试大纲是基本一致的。

图1 试卷中各题型的重要性比例

接下来,继续对194名大学生54个组合题目的试题重要度进行分析,我们发现,试卷所有题目的试题重要度基本呈正态分布,如图2所示。共有28个题目的试题重要度在0.4～0.6之间,占全部54个题目的大多数;重要度在次高区间0.6～0.8和次低区间0.2～0.4的试题数量分别为8个和11个;重要度在最低区间0～0.2的试题只有6个;重要度在最高区间0.8～1.0的试题仅1个。我们可以对这些重要度比较低的题目进行修改和质量提升。从图2可以看出,总的来话,英语试卷的试题重要度分布情况与命题预期目标基本一致,说明这份试卷内容主次分明,质量较高,基本符合教学大纲和考试大纲要求。

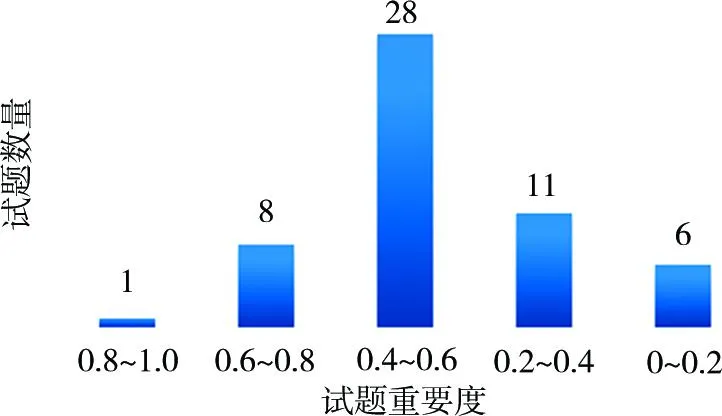
图2 重要度区间的题目数量分布

3 结语

在已有研究[14-18]的基础上,将粗糙集理论应用于大学英语考试命题,利用粗糙集相对正域、冗余属性和属性重要度等重要概念,提出试题冗余性定性判别方法,并提出试题重要度的定量度量方法,从而建立了基于粗糙分析的大学英语考试质量提升模型。实验数据来源于参与湖南科技大学2021-22-2学期期末英语考试的大二非英语专业学生。实验先对194名大学生42个组合题目的冗余性进行分析,发现2组组合题目是冗余的,说明这2组题目是不太科学合理的;再对194名大学生的4个题型和54个组合题目的重要度进行计算,发现所有试题的重要度基本呈正态分布,只有少数几个题目的重要度较低。本研究结果能指导我们对少数冗余的或者重要度较低的考试题目进行修改和质量提升,有效提高了试卷的命题质量,对指导大学英语教学工作、提高大学英语教学质量具有重要指导意义。