初中数学教科书非文本元素特点及功能研究——以浙教版为例

李玲珠，陈秋雨

初中数学教科书非文本元素特点及功能研究——以浙教版为例

李玲珠，陈秋雨

（华东师范大学 数学科学学院，上海 200241）

非文本元素是数学教科书不可或缺的组成部分．但有研究者发现，部分NTEs存在偏装饰、功能单一、与数学联系不紧密的现象．以浙教版初中数学教材为例，通过比较NTEs的类别与功能分析其合理性．研究发现，浙教版八年级的NTEs数量最多，九年级平均密度最大．类别与功能上，NTEs在数学类的数量最多，以解释性功能为主．此外，生活类的NTEs以装饰性功能为主，数学史类NTEs以装饰性和解释性功能为主．未来，NTEs可在与数学内容的实质性联系以及功能的丰富性上作进一步考虑．

浙教版；非文本元素；类别；功能；教材分析

1 问题提出

数学教材的研究与发展正日益受到国内外研究者的重视[1-2]．目前，大部分研究集中于教科书文本或知识点的比较[3-4]，对非文本的分析，比如插图，相关研究还比较少．教科书插图作为文本信息的补充，能够起到美化、吸引学生注意以及提高学生学习兴趣的作用[5-6]，部分插图还能帮助学生发现文本中不容易察觉的信息[7]．有研究者认为，学生在课堂上依赖插图来获取知识[8]．在数学学科中，教科书插图还是学生理解数学知识、感悟数学价值的基本素材[9]，能够增强教科书的可读性与趣味性[10-11]．《义务教育数学课程标准（2011年版）》在教材编写建议中指出“学习素材的选择，图片、情境、实例与活动栏目等的设置……都应当与所安排的数学内容有实质性联系，有利于提高学生对数学实质的理解，有利于提高学生对所学内容的兴趣”[12]．2022年版课程标准进一步阐述为“教材应具备可读性，图文并茂……增加学习的趣味性”[13]．

然而，有研究发现，部分教科书插图没有明显教学目的，它们要么仅作装饰页面之用，要么只是作为单一元素来描绘文本信息[14]；张维忠等人发现，教科书插图存在准确性低、联系性弱、不够简洁等质量问题[9]．此外，教育部也高度重视教科书中的插图问题，并于2022年5月28日部署了对全国中小学教科书内容、插图等进行全面排查的决定[15]．

基于此，为了厘清插图在教科书中的作用，提高插图的使用价值，同时为未来数学教科书编写者提供关于插图的更合理的建议，以浙江教育出版社初中数学教科书（以下简称“浙教版”）为例，对其中的插图进行分析．研究主要从两方面入手：第一，浙教版插图主要有哪些类别；第二，每类插图有哪些功能，合理性如何．此外，为了更好地表达插图在数学教科书中所表示的意义，将数学教科书中的插图命名为“非文本元素”（Non-textual elements，简称NTEs）．研究问题如下．

（1）浙教版非文本元素的类别和功能分别有哪些？总体分布情况如何？

（2）各类别分别包含哪些功能？合理性如何？

2 非文本元素的内涵

教科书插图作为一种图形语言[16]，以直观、形象的特点插附于文字中，是文字系统的补充[17]．不同学科插图的表现形式、作用各不相同，比如语文教科书中的插图以图片、绘画为主要表现形式，目的是再现故事情节、提升学生阅读的能力[18]；科学教科书中的插图以实验照片为主，为了展现实验操作的步骤和现象；而体育教科书中的插图主要以人物动作照为主，是教学、模仿正确运动姿势的最直观表现．

在数学学科中，教科书中的图形语言不仅包括照片、图画，还包括表格、统计图以及以点、线、面为主要组成元素的几何图形．虽然很多研究者用“插图”或“数学插图”代之，如张楠、黎露等在分析与比较中学数学教科书中的相关内容时用了“插图”一词[19-20]；王一儒等将初中数学教科书中出现的图表统称为插图[21]；刘明将穿插在数学习题中且能为题目提供背景信息或文字内容的图片称之为数学插图[22]．就数学的特点而言，用“插图”或“数学插图”指代教科书中的所有图片、几何图形、图表等似乎不太恰当．故Kim提出“非文本元素”一词，并对其进行了界定．他认为非文本元素是一种由非纯语言、数字或数学符号组成的表征，包括图片表征和数学表征．图片表征是指照片和描绘现实世界中物体图形的图片，数学表征是指图表和抽象的数学几何图形等[6，9]．与非文本元素类似，Gunzel用“非语言元素”（Nonverbal elements）指代数学插图[23-24]．

对比“插图”一词，用“非文本元素”或“非语言元素”来描述数学教科书中的图形语言更为贴切．因此，用“非本文元素”一词来代表数学教科书中所有的照片、图画、几何图形、统计图表等，结合Kim的定义，最终将非文本元素定义为：插附于数学教科书中的由非纯语言、数字、符号组成的一类照片、图画、小贴士、几何图形、统计图表等，它们具有图象表征或数学表征的特点，并以直观的方式传递信息，是文字信息的补充．非文本元素主要有以下特点：

①非纯文本性，即不是由纯文字语言组成的；

②非纯符号性，即不是由纯数字、符号等组成的；

③补充性，即对文本信息具有补充作用；

④数学性，即部分图片表现为明显数学特点，比如几何图形、数据图表等．

为了与纯数字、符号、公式等进行区分，研究用Kim的“勾股定理的例子”作进一步解释：比如方程2+2=2不是非文本元素，因为它仅由符号组成；然而，如果用一幅带有符号的直角三角形图片来解释（如图1），则该图片是非文本元素[6]．

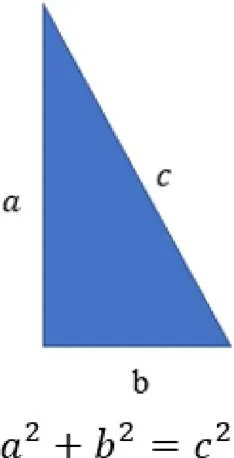
图1 带有符号标记的直角三角形图片

3 NTEs的类别与功能

3.1 NTEs的类别

在教科书插图的分类上，Levie和Lentz曾将其分为代表性图片和无代表性图片，代表性图片是指那些普通的图片和显示事物外观的图片，而无代表性图片主要指地图、图表和图形的组合[5]．针对具体学科，研究者们往往有更细致的划分，以数学教科书为例，有按位置分、按内容分、按组织形式分、按学科特点分等．

按所处的位置分，NTEs可分为章首图、栏目图、文中图和练习题图等[21，25]．

按内容分，NTEs可分为数据图表、模型图、卡通图、生活图、史料图[26]．

按组织形式分，NTEs可分为独立图、发散图、序列图和多层图[25]．

按数学学科特点分，NTEs可分为生活类、纯数学类、肖像图和实验图等[25]，也有研究者将其分为几何图形、图表、图片、组合图以及其它类[23]．因后者的分类更突出数学中的几何图形，故张维忠和胡智慧对此作了进一步解释，比如数轴、直角坐标系、直线、抛物线、双曲线等为精确的几何图形，精确的几何图形与图片的结合归为图片类[24]．

此外，随着时代的变迁，NTEs在数学教科书中的位置、组织形式等也发生了变化．以人教版初中数学教科书为例，研究者发现NTEs的位置已经由新授课图、课后练习图、章节小结图拓展到了章节导入图、新授课图、栏目图、课后练习图、章末小结图、探究与阅读模块图；组织形式上，NTEs也从单一走向多样化；功能上，NTEs已经发展为装饰图、数学史图、提供数据信息图、数学实验探究图、引导数学思考图、数学模型示意图以及多功能结合型图[27]．

研究结合浙教版NTEs的特点，采用了“按数学学科特点”的分类方法，在生活类、数学类、组合类、其它类的基础上，将肖像图改为了数学史类，增加了ICT类．最终，NTEs分为6类，分别是生活类、数学类、数学史类、ICT类、组合类和其它类．

生活类：主要指生活中常见的人、物、场景等实物照片或绘画图，也包括科技航天照、学科专业图等，比如大桥、飞船、艺术画、烧瓶（化学）、红细胞（生物）等（如图2）．

图2 生活类插图[28]

数学类：主要指精确的几何图形、概念图、流程图、结构图、关系图等，也包括图表、工具图（比如量角器、圆规等图）、用物品摆成的数学图形（比如火柴摆出平行四边形）等（如图3）．

图3 数学类插图[29]

数学史类：主要体现数学历史的图或数学家肖像等（如图4）．

图4 数学史类插图[29]

ICT类：主要指计算器、计算机等与科学技术相关的图（如图5）．

图5 ICT类插图[29]

组合类：主要指系列图、两种类型或以上的合成图，如折纸的步骤图、生活类与数学类的合成图等（如图6）．

图6 组合类插图[29]

其它类：主要指问卷调查表、自我评价表、数学小贴士、图标logo等（如图7）．

图7 其它类插图[29]

3.2 NTEs的功能

一般而言，教科书插图的功能有两种，即认知功能和非认知功能[30]，也有研究者将其细分为：演示功能——使文本更具体、连贯、便于理解；组织功能——用于逐级指导组建文本各元素之间的一致性关系；解释功能——解释文本片断所需的上下文关系[31]．Tang根据Hunter等人的研究将教科书插图分为装饰、强化、解释、总结和比较功能[8]．此外，从阅读和科学教科书的特点出发，研究者将插图细分为装饰性、表征性、组织性、解释性和转换性功能[6]．黎露和李三平认为，上述装饰功能属于非认知功能，而表征、组织等属于认知功能[20]．

在数学教科书中，Gunzel与Binterova对精确的几何图形进行了功能的细分，主要有探究性功能、解释性功能、建构性功能[23]．张维忠与胡智慧在Gunzel等人的基础上，进一步对图片或照片、统计图表、表格、其它图片等进行了细分．其中，图片或照片主要有4种功能，分别是装饰性功能、表征性功能、解释性功能和探究性功能；统计表与统计图主要体现一种功能，即呈现数据及趋势；表格主要有两种功能，分别是任务性和评价性功能；其它图片有两种功能，分别是数学文本和阐释数学本质的功能[24]．张文宇和任乙佳对比中美小学数学教科书后认为，NTEs主要有装饰性、表征性和解释性3种功能[26]．孙庆括在此基础上增加了组织性功能[25]．王一儒和刘学利参考Mayer等人的分类，也将NTEs的功能分为了装饰性、表征性、组织类和解释性4类[21]．

综上，数学教科书中的NTEs除了有作为教科书插图的一般性功能（即装饰性、表征性、组织性和解释性）之外，还具有体现数学探究特点的功能，即探究性或建构性．研究者将装饰性、表征性、组织性、解释性和探究性作为数学教科书NTEs的主要功能．

结合浙教版中NTEs的特点发现，仅有以上5种功能，无法将教科书中的“自我评价表”、课题学习中的“问卷调查表”等纳入其中，故最终增加了“其它”功能，主要包括每章章末的自我评价表、课题学习中的问卷调查表等．以下是6种功能的具体解释．

装饰性：与数学内容无实质性联系的图，主要以美化教科书、吸引学生注意力，激发学生学习的兴趣为主（如图8）．

图8 宇航员在月球[29]

表征性：表征数学概念的图[24]（如图9）．

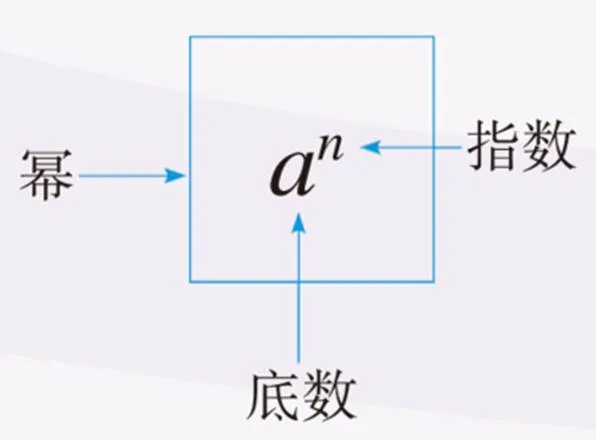
图9 幂的概念[29]

组织性：用文本框、箭头、大括号等组织起来的知识的结构图、流程图（如图10）．

图10 概念之间联系的结构图[29]

解释性：为文本提供附加信息，或显示原型示例[23]，或解释教科书中文本信息所表达的意思的图[24]（如图11）．

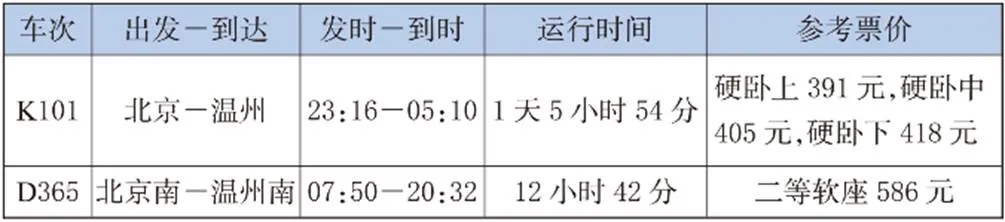
图11 用于解释并补充文本信息的火车时刻信息表[29]

探究性：文本要求的用于求解或进一步探索、创造的图形[23]，比如填表、画图、折纸、剪裁等（如图12）．

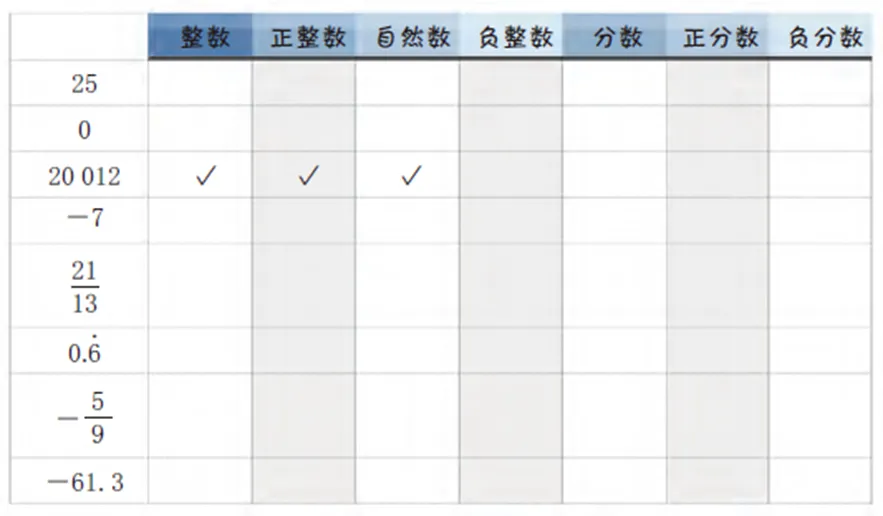
图12 填表题[29]

其它：主要指自我评价表、问卷调查表等（如图13）．

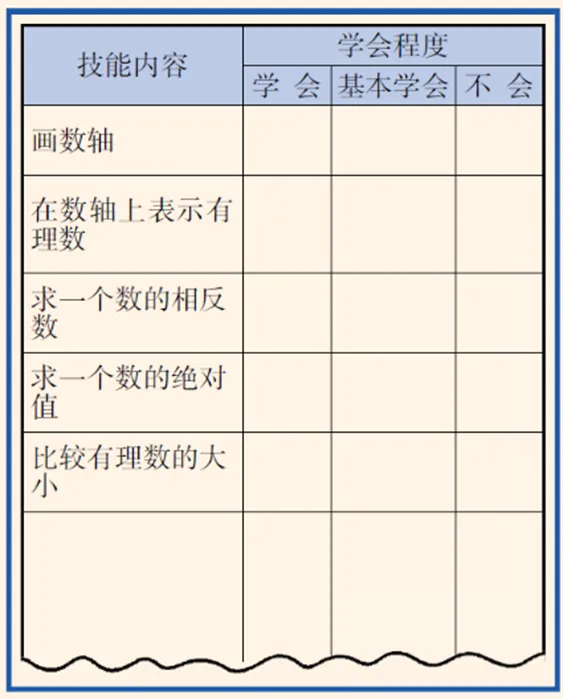
图13 章末自我评价表[29]

4 研究过程

研究以浙教版初中数学六册教科书中的NTEs为研究对象，在研究过程中，先根据NTEs的分类标准对类别和功能进行划分．如果某一张NTEs出现多种类别或功能，以主要类别或功能为依据划分．由于6册NTEs共计2 210张，数量较大，最后决定抽取其中20%计算一致性，作为NTEs的信度．

两位数学教育专业的研究者分别对NTEs的类别和功能进行了一致性分析．

首先，两位研究者对某一章的NTEs进行了类别和功能的独立编码，对不一致的编码进行讨论，重新修订编码标准．

接着，研究者按比例抽取6册数学教科书中的NTEs，每一册采用分层抽样的方法．

然后，两位研究者分别对20%的NTEs进行类别和功能的独立编码．

最后，对两位研究者分别编码的类别和功能的NTEs进行一致性检验．

计算得到，类别=0.81，功能=0.83，这说明类别和功能都有比较高的一致性．

5 研究结果

5.1 总体分析

浙教版初中数学6册教科书NTEs共计2 210张（见表1）．其中八年级NTEs数量最多，有788张；九年级其次，有746张；七年级最少，有676张．6册教科书NTEs总体平均密度为2.33（平均密度=NTEs总数/总页数），单册平均密度排序从高到低为：九年级下册（3.18）>九年级上册（2.73）>八年级上册（2.64）>八年级下册（2.09）>七年级上册（2.04）>七年级下册（1.73）．

从类别来看，6类NTEs按数量从高到低分别为：数学类（1 521）>生活类（304）>组合类（219）>其它类（112）>数学史类（28）>ICT类（26），其中数学类的数量远多于其它几类，占总数的68.82%．

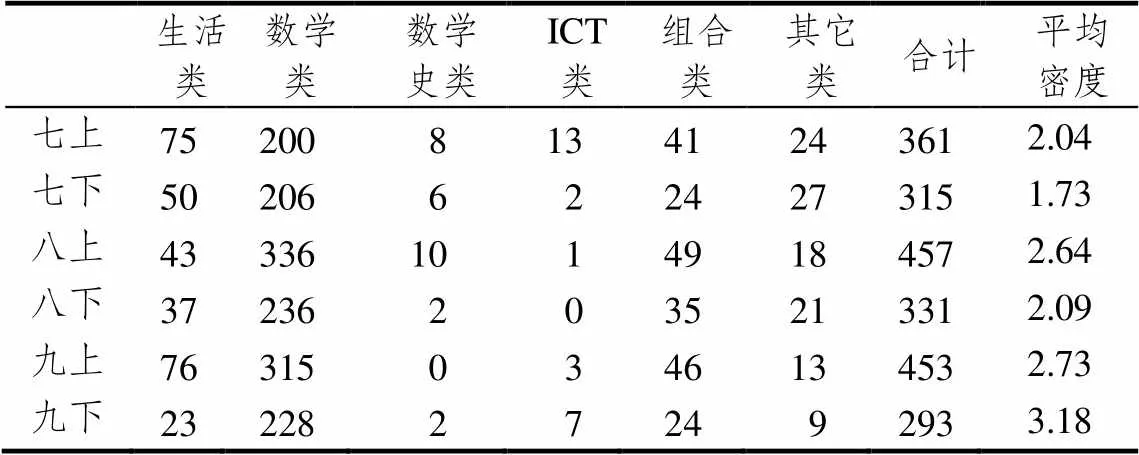
表1 各册教科书类别的分布

从功能分布来看（见表2），6种功能的NTEs按数量从高到低为：解释性（1 508）>探究性（396）>装饰性（224）>表征性（41）>其它（31）>组织性（10），其中解释性的数量远多于其它几种功能，占总数的68.24%．

综上，首先就年级的数量和平均密度而言，七年级NTEs的数量最少，平均密度也最低；八年级NTEs的数量最多，但平均密度却是九年级最高．其中的原因，可能与各年级教科书的页数和具体内容的分布有关．研究发现：浙教版教科书的页数随着年级的增加而减少；内容上，七年级以“数与代数”为主，八、九年级以“图形与几何”为主．研究发现，图形与几何内容产生的NTEs数量比数与代数更多[32]．基于以上两点，不难得出，七年级不管是NTEs数量还是平均密度，都是最少（或最低）的．

其次，在类别上，各册教科书以数学类为主，主要原因与数学本身的特点以及初中数学强调图形与几何密不可分．一方面，抽象是数学的特点之一，这就意味着数学教科书中的NTEs大多以点、线、面的形式存在；另一方面，图形与几何章节在初中数学教科书中占比是最大的，在浙教版中，6册教科书共计30章，图形与几何有12章，占比40%．而在图形与几何中，精致的几何图形是其主要表现形式，这就大大增加了数学类NTEs的数量．

最后，在功能上，各册教科书以解释性功能为主，这一结论与王一儒、刘学利的研究一致[21]．背后的原因可能与NTEs本身的定义相关，即它是文字信息的补充，能为文字信息起到解释的作用．

5.2 类别—功能分析

类别—功能的分析主要从类别出发，分析它们分别涉及哪些功能，以获得每一类别所属的主要功能，然后进一步分析其合理性．

5.2.1 生活类

生活类NTEs共有304张，占NTEs总数的13.76%，功能上涉及3种，分别是装饰性、解释性和探究性（如图14）．其中，装饰性功能最多，有195张，占生活类NTEs总数的64.14%．其次是解释性功能，有103张，占33.88%．探究性功能最少，只有6张，占比1.97%．3个年级中，七年级生活类NTEs数量最多，有125张；九年级其次，有99张；八年级最少，有80张．

此外，结合表2可知，装饰性功能主要体现在生活类中，因为总计224张装饰性的NTEs，生活类中有195张，占比达87.05%．

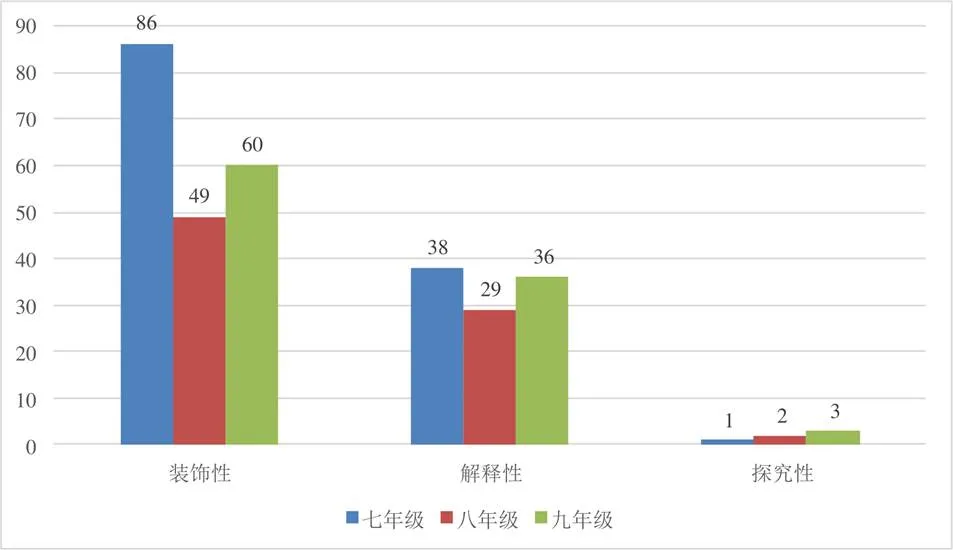
图14 生活类NTEs功能分布情况

具体分析生活类的装饰性功能发现，它们大多与数学内容并无实质性联系，仅仅起到了装饰作用，比如图15中的“鸵鸟蛋”和“杭州湾跨海大桥”．这一结论与Kim、Nag Chowdhuri的研究一致，他们认为装饰性NTEs主要以美化教科书为主，与数学内容的联系比较弱[6，33]．虽然美化数学教科书、吸引学生阅读兴趣的NTEs必不可少，但如果装饰性太多，不免让人怀疑教科书的质量与作用．张维忠等人通过对比中美初中数学教科书中的NTEs发现，浙教版的NTEs确实存在联系性弱的情况[9]．生活类NTEs的主要目的是为了体现数学与生活的联系，如果这种联系能够更好地体现数学在生活中的作用，如图16“三角形在生活中的应用”，效果是否会更好？

图15 鸵鸟蛋与杭州湾跨海大桥[29]

图16 三角形在生活中的应用[34]

5.2.2 数学类

数学类共有1 521张（如图17），占NTEs总数的68.82%．其中，解释性功能数量最多，有1 156张，占数学类NTEs总数的76.00%；探究性功能其次，有312张，占比20.51%；表征性和组织性功能比较少，分别是40张（2.63%）和10张（0.66%）；装饰性和其它功能分别只有2张（0.13%）和1张（0.07%）．此外，3个年级中，八年级数学类NTEs最多，有572张；九年级其次，有543张；七年级最少，有406张．

图17 数学类NTEs功能分布情况

进一步分析发现，解释性功能作为数学类NTEs的主要功能是合理的．以八年级上册“1.1 认识三角形（2）”中的例2（如图18）为例，图中右侧三角形是对文本信息的进一步解释，它以几何图形的形式更加清楚、直观地展现了题目的信息，降低了文字语言的抽象感，能够有效帮助学生理解题目所表达的意思．

图18 数学类NTEs作为解释性功能的例子[34]

此外，表征性、组织性、探究性功能的NTEs数量虽然不及解释性功能多，但与各自的总数相比，发现这3种功能基本分布于数学类中（见表3）．6册教科书表征性功能的NTEs共41张，数学类占了40张；组织性功能的NTEs共10张，这10张都属于数学类；探究性功能的NTEs共396张，数学类占了312张．由此可知，浙教版NTEs在涉及概念、知识的结构以及对知识的探索等上，都非常重视数学性，体现了数学的特点．

表3 数学类NTEs在各功能上的分布

5.2.3 数学史类

数学史类NTEs共有28张（如图19），占总数的1.27%．功能上，数学史类NTEs只涉及装饰性和解释性功能，且两种功能的数量相近．年级比较中，数学史类的NTEs分布并不均匀，七、八年级所占数量比较多，分别有14张和12张，九年级只有2张．进一步分析发现，七年级分布比较均匀，而八、九年级的分布差异较大，其中八年级主要分布于八年级上册，九年级都分布于九年级下册．功能上，各个年级分布比较均匀．

图19 数学史类NTEs功能分布情况

具体分析数学史类NTEs的装饰性和解释性功能发现，装饰性以数学家头像为主，解释性以补充解释中外古代数学思想方法为主（如图20）．从数学史材料设置的目的（开阔学生的视野，丰富教材使用者的素材资源[12–13]）而言，上述两种功能的存在是合理的，但就其融入方式而言，可作进一步探讨．蒲淑萍和汪晓勤曾就数学史材料如何更好地融入教科书给出了5种模式，分别是点缀式、附加式、复制式、顺应式、重构式[35]．参考这5种模式，数学史类NTEs的表现形式是否也可稍作调整，使之更加丰富多样？比如图20中右半部分，可以用找规律的方式让学生进行探索，学生在思索数字间关系的过程中，不正是一种历史的再发现吗？

图20 埃拉托斯特尼肖像与杨辉三角[28]

5.2.4 ICT类

ICT类NTEs共有26张，占NTEs总数的1.77%，功能上只涉及解释性功能．具体分析可知，ICT类NTEs的解释性主要用于介绍软、硬件设备的功能、指导操作等，比如七年级上册“2.7 近似数”一节中计算器的介绍以及例1中如何用计算器进行计算的指导（如图21）．

图21 计算器及其操作[29]

年级比较中，ICT类的NTEs分布并不均匀，其中七年级与九年级分别有15和10张，八年级只有1张（在八年级上册中）．未来八年级在ICT类的NTEs数量可适当增加，尤其可以考虑增加ICT类的探索性功能．比如八年级上册“2.3 等腰三角形的性质定理（2）”中，教科书介绍了如何用“几何画板”软件探索等腰三角形三线合一的性质（如图22）．书中的图是解释性的，但学生很难从这幅静态的图中想象“三线合一”．如果该题的图改为借助软件画三角形的系列图，从一般三角形到等腰三角形，每一位学生可以根据自己“几何画板”中的样子将它描绘到书上，那么等到系列图完成后，学生是否就能从这一幅幅静态的画中看到其中动态的变化？是否能够更好地帮助学生理解？

图22 “几何画板”软件探索等腰三角形三线合一[34]

5.2.5 组合类

组合类NTEs共有219张（如图23），占NTEs总数的9.91%，功能上涉及装饰性、表征性、解释性和探究性．其中，解释性功能有183张，占组合类NTEs总数的83.56%；其次是探究性和装饰性功能，分别有24张和11张，占比为10.96%和5.02%．表征性功能只有1张，位于九年下册．

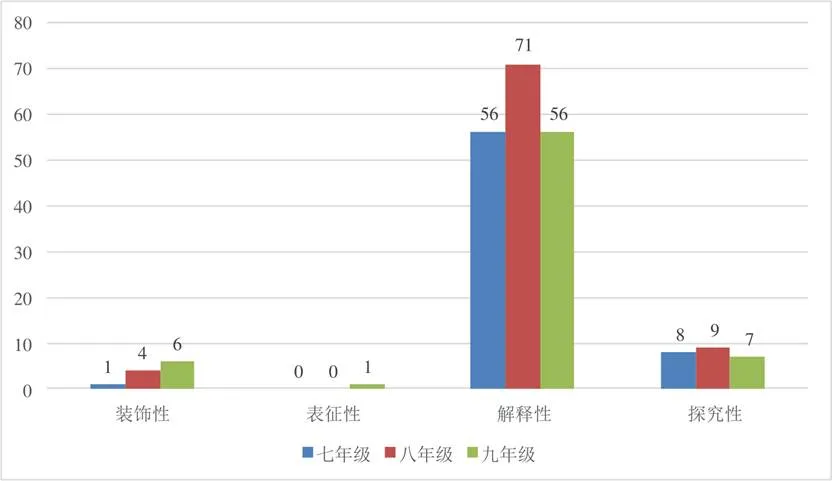
图23 组合类NTEs功能分布情况

具体分析组合类NTEs的解释性功能发现，这类NTEs以生活类与数学类的组合为主（如图24）．它在生活与数学之间起到了很好的桥梁作用，较好且合理地体现了数学源于生活又用于生活的思想．

图24 生活类与数学类的合成图[36]

5.2.6 其它类

其它类NTEs共有112张（如图25），占NTEs总数的5.07%，功能上主要集中于解释性、探究性和其它功能，装饰性功能只有1张．由图可知，探究性功能数量最多，有54张，占比48.21%，主要分布于七、八年级中；其它功能有30张，占比26.79%，年级分布比较均匀；解释性功能的数量略低于其它功能（27张，占比24.11%），主要分布于七年级；装饰性功能的1张NTEs分布于七年级上册中．

此外，结合表2，从功能的角度分析后发现，其它功能的NTEs主要体现在该类别中（其它功能的NTEs共31张，在该类别上有30张）．

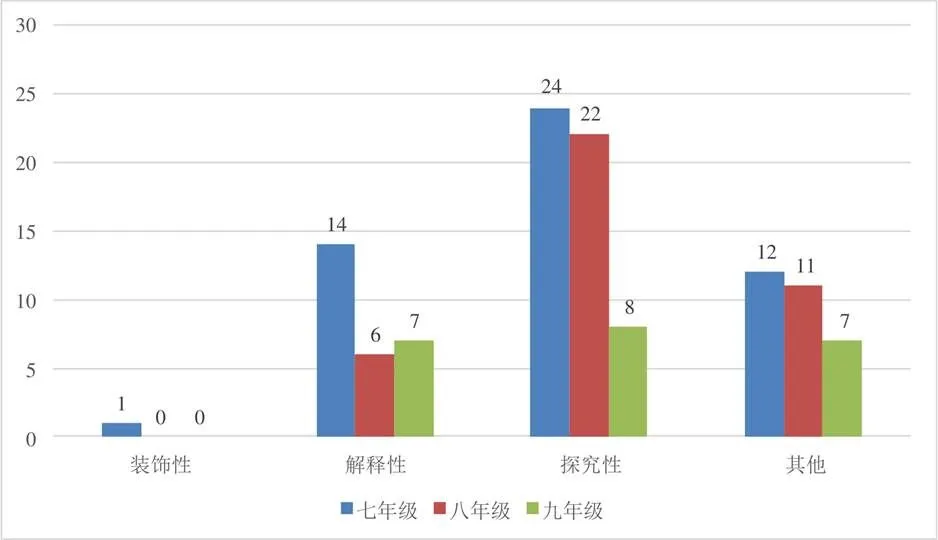
图25 其它类NTEs功能分布情况

具体分析发现，其它类NTEs主要以教科书中的数学小贴士“想一想”“注意”以及每章章末的自我评价表为主（如图26）．其中，“想一想”属于探究性功能，“注意”属于解释性功能，自我评价表属于其它功能．

图26 数学小贴士与自我评价表[36]

6 总结与展望

6.1 总结

以浙教版为例，探究了教科书NTEs的类别、功能以及相互之间的关系．总体而言，从各年级NTEs的数量分布来看，八年级NTEs的数量最多，九年级NTEs的平均密度最大．具体地，按类别划分，6类教科书NTEs的数量从高到低分别是数学类、生活类、组合类、其它类、数学史类和ICT类．数学类NTEs的数量远多于其它几类，这可能与数学本身的特点以及初中教科书注重“图形与几何”内容相关．按功能划分，6种功能的教科书NTEs数量从高到低分别是解释性、探究性、装饰性、表征性、其它和组织性．解释性功能数量最多的原因可能与NTEs本身的定义有关．

（1）数学类和组合类主要以解释性功能为主，体现了一定合理性．

数学类NTEs以直观的方式补充、解释文字信息，能够降低知识的难度．组合类NTEs与生活联系紧密，较好地体现了数学源于生活又用于生活的思想．

（2）生活类、数学史类、ICT类NTEs在分布或功能上仍有进一步讨论的可能．

生活类NTEs以装饰性功能为主，但装饰性的生活类NTEs只能起到美化教科书或吸引学生兴趣的作用，与数学内容的联系比较弱．未来还需重新考虑生活类NTEs的表现形式，比如将部分装饰性功能的NTEs改为与数学知识有实质性联系的生活照等．

数学史类NTEs的功能性相对合理，主要以装饰性和解释性功能为主．装饰性功能主要指数学家的肖像图，解释性功能以解释中外古代数学思想方法为主．但在年级的分布上并不均匀，其合理性有待进一步讨论．未来可考虑：①适当增加九年级数学史NTEs的数量；②将七、八年级部分装饰性、解释性的NTEs改为探索性的NTEs，以增强其探索性与互动性．

ICT类NTEs以解释性功能为主，与数学史类相似，年级分布上并不合理．后期在年级上可考虑增加八年级ICT类NTEs的数量，在功能上可考虑将部分解释性的NTEs改为探索性的NTEs，以增强技术与数学更加紧密、实质性的联系．

此外，从各功能所包含的类别来看，装饰功能的NTEs主要体现了生活性．表征性、组织性、解释性、探究性功能的NTEs主要体现了数学性．

6.2 创新与不足

研究的创新之处主要有两点：一是结合数学的特点给出了NTEs的定义，并结合具体教科书——浙教版的特点，系统地梳理了NTEs的类别与功能；二是基于从类别、功能之间的相互关系，探讨了每一类NTEs的功能的合理性，并对NTEs的类别与功能给出了可进一步改进的建议，具有一定参考价值．

当然，研究也存在不足．

首先，在编码过程中发现部分NTEs涉及多种功能，正如Levie与Lentz在研究中指出的“这些功能并不是相互独立的，某一张NTEs可能存在多种功能”[5]，但研究者只参考并选取了NTEs的最主要功能．基于这一点，后期研究可以在NTEs功能的编码上作进一步改进．

其次，量化的NTEs只是一个相对标准，并不能仅根据类别或功能的数量多少做出绝对判断，更合理的评判标准应该结合真正的使用者——教师和学生的看法．

最后，类别和功能只是NTEs分析的第一步，若要完善NTEs在教科书中的作用，还需更多的实证研究．

致谢：感谢华东师范大学数学科学学院特聘教授、亚洲数学教育中心主任范良火教授的指导！

[1] 王思凯，李沐慧，徐斌艳．国际视野下数学教材研究的行动与展望——基于ICME-14数学教材研究的分析[J]．数学教育学报，2022，31（3）：15-19．

[2] 朱雁，倪明，孔令志，等．数字时代中的数学教材研究与开发及使用——第三届国际数学教材研究和发展会议综述[J]．数学教育学报，2020，29（2）：94-99．

[3] 石义娜，丁红云，夏小刚．初中数学教材中的问题编写及其价值取向变化——以人教版（1978—2020年）“有理数”内容为例[J]．数学教育学报，2022，31（2）：35-39．

[4] 俞蓉，赵世恩．中英小学数学教材中“图形的运动”难度比较研究[J]．数学教育学报，2022，31（6）：80-86．

[5] LEVIE W H, LENTZ R. Effects of text illustrations: A review of research [J]. Educational Communication and Technology, 1982, 30 (4): 195-232.

[6] KIM R Y. The quality of non-textual elements in mathematics textbooks: An exploratory comparison between South Korea and the United States [J]. ZDM, 2012, 44 (2): 175-187.

[7] ARCAVI A. The role of visual representations in the learning of mathematics [J]. Educational Studies in Mathematics, 2003, 52 (3): 215-241.

[8] TANG G M. Textbook illustrations: A cross-cultural study and its implications for teachers of language minority students [J]. The Journal of Educational Issues of Language Minority Students, 1994 (13): 175-194.

[9] 张维忠，胡智慧．中美初中数学教科书插图质量的比较[J]．数学教育学报，2022，31（1）：64-69，84．

[10] 陈翠花，周志鹏．品味初中数学教材的插图文化[J]．数学教育学报，2008，17（3）：98-99．

[11] 张维忠，孙庆括．多元文化视野下的数学教科书编制问题刍议[J]．全球教育展望，2012，41（7）：84-90．

[12] 中国人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学，2012：60-70．

[13] 中国人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学，2022：94-95．

[14] MAYER R E. Commentary comprehension of graphics in texts: An overview [J]. Learning and Instruction, 1993, 3 (3): 239-245.

[15] 中华人民共和国教育部．教育部关于人教版小学数学教材插图问题的回应[EB/OL]．（2022-05-28）[2023-02-10]．http://www.moe.gov.cn/jyb_xwfb/gzdt_gzdt/s5987/202205/t20220528_632055.html．

[16] 张伍秋，蓝云．教材插图艺术探[J]．有色金属高教研究，1994，10（3）：97-103．

[17] 张贺华．三～六年级科学教科书插图的研究——以河北人民出版社《科学》为例[D]．上海：华东师范大学，2010：7．

[18] 乔思瑾．教科书插图创作研究——以统编小学语文教科书为例[J]．课程·教材·教法，2020，40（9）：74-80．

[19] 张楠．初中数学教材插图的分析与比较[D]．北京：首都师范大学，2014：3．

[20] 黎露，李三平．初高中数学教材插图的比较研究[J]．初中数学教与学，2021，28（10）：1-3，6．

[21] 王一儒，刘学利．人教版初中数学教科书插图编排特点研究[J]．内蒙古师范大学学报（教育科学版），2021，34（2）：120-125．

[22] 刘明．数学插图“负效应”的分析及应对策略[J]．教学与管理，2012，29（11）：46-47．

[23] GUNZEL M, BINTEROVA H. Evaluation of nonverbal elements in mathematics textbooks [J]. Universal Journal of Educational Research, 2016, 4 (1): 122-130.

[24] 张维忠，胡智慧．数学教科书中的非语言元素分析——以浙教版八年级数学教科书为例[J]．浙江师范大学学报（自然科学版），2019，42（3）：351-355．

[25] 孙庆括．我国高中数学教科书插图的分类、功能与运用策略[J]．课程教学研究，2018，7（7）：45-47．

[26] 张文宇，任乙佳．中美小学数学教科书插图比较研究[J]．教学与管理，2017，34（36）：121-124．

[27] 潘小勤，张维忠．数学教科书中的插图变迁分析——以人教版初中数学教科书为例[J]．中学数学杂志，2019，39（12）：5-9．

[28] 范良火．义务教育教科书·数学（七年级下册）[M]．杭州：浙江教育出版社，2021：25-91．

[29] 范良火．义务教育教科书·数学（七年级上册）[M]．杭州：浙江教育出版社，2021：5-172．

[30] 曾天山．国外关于教科书插图研究的述评[J]．外国教育研究，1999，26（3）：20-23．

[31] 李兴韵，温小英．国外教科书插图效应和功能研究的启示[J]．现代教育科学，2013，30（10）：62-64．

[32] 丛龙琦．中、新、美初中数学教科书的非语言元素比较分析[D]．天津：天津师范大学，2020：36．

[33] NAG CHOWDHURI M. Exploring modes of engagement within reform-oriented primary mathematics textbooks in India [J]. Educational Studies in Mathematics, 2022, 110 (2): 331-351.

[34] 范良火．义务教育教科书·数学（八年级上册）[M]．杭州：浙江教育出版社，2021：8-59．

[35] 蒲淑萍，汪晓勤．数学史怎样融入数学教材：以中、法初中数学教材为例[J]．课程·教材·教法，2012，32（8）：63-68．

[36] 范良火．义务教育教科书·数学（九年级下册）[M]．杭州：浙江教育出版社，2021：5-40．

A Study on Characteristics and Functions of Non-textual Elements in Junior High School Mathematics Textbooks: An Example of Zhejiang Education Press Series of Textbooks

LI Ling-zhu, CHEN Qiu-yu

(School of Mathematical Sciences, East China Normal University, Shanghai 200241, China)

Non-textual elements (NTEs) are an indispensable part of mathematics textbooks. However, some researchers have found thatsome parts of NTEs are partial to decoration, have single functions, and are not closely related to mathematics. Therefore, in this study, we take the ZEP series of mathematics textbooks as an exampleto analyze the rationality of NTEs by comparing the categories and functions. The results show that Grade 8 contains the largest number of NTEs, and the average density of NTEs in Grade 9 is the highest. In terms of categories and functions, NTEs have the largest number in the mathematics category and mainly have explanatory functions. In addition, we found thatNTEs in the life category mainly have decorative functions, while NTEs in the life category mainly have decorative and explanatory functions. In the future, NTEs can be further considered in terms of substantive connection with mathematical content and richness of functions.

Zhejiang education press (ZEP); non-textual elements; category; function; textbooks analysis

2023–09–09

华东师范大学“幸福之花”先导研究基金项目——数学教材电子资源的开发与使用效果研究（2019ECNU-XF2H004）

李玲珠（1990—），女，浙江宁波人，博士生，主要从事教师专业发展、教材发展与比较、数学教学研究．

G423.3

A

1004–9894（2024）01–0008–08

李玲珠，陈秋雨．初中数学教科书非文本元素特点及功能研究——以浙教版为例[J]．数学教育学报，2024，33（1）：8-15．

[责任编校：陈汉君、张楠]