作答时间与反应依赖关系建模：基于双因子模型视角*

郭小军 柏小云 罗照盛

作答时间与反应依赖关系建模：基于双因子模型视角*

郭小军1柏小云1罗照盛2

(1赣南师范大学教育科学学院/教育经济研究中心, 江西 赣州 341000) (2江西师范大学心理学院, 南昌 330022)

在心理与教育测验中, 测验的计算机化越来越普遍, 使得被试作答的过程性数据的搜集也越来越便利。分层模型的提出为作答时间与反应的联合分析提供了一个基本的建模框架, 且逐渐成为当前最流行的方法。虽然分层模型被广泛使用, 但仅仅通过参数间的关系还不能很好地解释作答时间和反应之间的关系。因此, 一些研究者提出了一系列改进模型, 但仍然存在一些不足。基于双因子模型的新视角, 文中将测验的作答时间与反应分别视为测量被试速度和能力的两个局部因子, 而作答时间与反应又视为综合测量了被试的速度与准确率权衡的一般能力或全局因子。基于此, 文中提出双因子分层模型, 以探讨作答时间与反应的依赖关系。模拟研究发现Mplus程序能有效估计双因子分层模型的各参数, 而忽视作答时间与反应依赖关系的分层模型的参数估计结果存在明显的偏差。在实例数据分析中, 相较于分层模型, 双因子分层模型的各模型拟合指数表现更好。此外, 不同被试在不同项目上的作答时间与反应存在不同的依赖关系, 从而对被试的作答准确率与时间产生不同的影响。

作答时间, 反应, 依赖关系, 分层模型, 双因子模型

1 引言

随着计算机在测验实施中的普及, 心理与教育测验也通常以计算机化的形式进行。计算机化的测验不仅能非常便捷地采集被试的作答反应数据, 还能获得被试的作答时间数据。在被试的作答数据中, 不仅作答反应能反映被试的重要作答信息, 作答时间也是被试的重要信息来源(Luce, 1986; van der Linden, 2009)。为了联合分析被试的作答时间与反应, van der Linden (2007)提出了分层模型(Hierarchical Model, HM), 它是目前最流行的建模方法之一。HM被广泛地应用于传统测验中(Klein Entink, Kuhn, et al., 2009; Lu et al., 2021; Scherer et al., 2015), 并逐渐扩展到认知诊断测验(Liang et al., 2023; Zhan et al., 2018)、人格测验(Ranger, 2013)以及认知实验(Loeys et al., 2011)的数据分析领域。

在HM建模框架中, 作答时间与反应模型构成第一层, 被试参数间的相关与项目参数间的相关构成第二层(van der Linden, 2007)。一些研究者发现作答时间与反应间存在依赖关系(Bolsinova & Tijmstra, 2016; van der Linden & Glas, 2010)。分层建模通过第二层参数间的相关来解释作答时间和反应之间的相关性, 但是仅仅通过参数间的相关只能解释作答时间与反应的部分相关。因此, 传统的HM无法有效地解释作答时间和反应之间的相关性影响。为了更好地反映作答时间与反应之间的依赖关系, 而不仅仅通过参数之间的相关性来获得, 一些研究者将作答时间与反应的依赖关系融入到分层模型中, 以进一步扩展模型。在作答时间与反应的残差相关上, Ranger和Ortner (2012)通过项目水平参数进一步解释两者的残差相关, 但并未考虑被试水平的依赖性; Meng等(2015)则基于被试与项目参数乘积来解释残差相关, 但是他们将项目参数固定为非负数, 导致在作答时间和反应之间的残差相关性上具有相同的符号。另外, 一些研究者将残差时间纳入作答反应模型中。Bolsinova, De Boeck和Tijmstra (2017)在反应模型中引入了残差时间, 并允许项目的残差相关性在符号上不同, 但并未考虑被试水平的差异。为了弥补这一不足, Bolsinova, Tijmstra和Molenaar (2017)进一步扩展至被试水平。Bolsinova和Molenaar (2018)则考虑了残差时间对作答反应的非线性影响。然而, 将残差时间直接添加到作答反应模型中会导致被试在所有项目上的作答准确率可以始终趋近于1, 违背了项目反应理论的基本假设。因此, 一些研究者单独构建线性(Guo et al., 2020)和非线性模型(郭小军, 罗照盛, 2019), 以探究残差时间对作答反应的影响, 但未考虑被试水平的差异。从上述模型可以看出, 不同研究者提出了一系列的模型, 然而总是存在不同方面的弊端, 模型也变得越来越复杂, 估计方法也更加困难, 这并不利于HM的应用。

在分析测验项目的依赖关系时, 最常用的项目反应理论模型包括双因子模型(bifactor model)和题组模型(testlet model)。双因子模型通过一般或全局因子(general factor)解释所有项目的共同变异, 同时使用局部因子或特定因子(specific factor)解释额外部分项目的共同变异(毛秀珍等, 2018)。比如在瑞文标准推理测验中, 不同维度的项目作答时间分别测了被试的知觉辨别速度、类同比较速度和比较推理速度等等, 同时整个测验的作答时间也测量了被试的一般速度特质(郭小军等, 2022)。在题组模型中, 多个项目共用相同刺激的情况构成题组(testlet), 此时被试对这些项目的作答依赖于对该内容整体的理解(詹沛达等, 2013)。例如, 在篇章阅读测验中, 属于同一篇章的多个项目就构成一个典型的题组(郑蝉金等, 2011)。关于双因子模型与题组模型的关系, 双因子模型通过特定因子与全局因子的载荷之比来反映题组效应的大小, 而题组模型是双因子模型的一个特例, 双因子模型更为复杂(魏丹等, 2017), 因此双因子模型更具有一般性。在心理与教育测验中, 不仅可以采集被试在测验项目上的作答时间, 还可以采集被试的作答反应。从双因子模型的视角看, 测验项目的作答时间与反应可以视为测量了不同的局部因子。具体而言, 测验的作答时间测量了被试的速度特质, 而测验的作答反应测量了被试的能力特质。同时, 被试在作答测验过程中还会受到时间与准确率的综合影响(Bolsinova, Tijmstra, & Molenaar, 2017; Davison et al., 2012), 即一般潜在特质或全局因子, 或速度与准确率权衡能力(Chen et al., 2018)。因此, 这样的测验结构非常符合双因子模型的特点, 为解决测验作答时间与反应依赖关系的联合分析提供了全新视角。

综合上述研究可以发现, 已考虑作答时间与反应依赖关系的HM存在不同方面的弊端。此外, 由于贝叶斯估计方法对数学基础要求较高以及适合该模型的统计软件的限制, 阻碍了HM的广泛应用。然而, 基于双因子模型视角提出的双因子分层模型(Bifactor hierarchical model, Bi-HM)为作答时间与反应的依赖关系提供了新的思路。而且Bi-HM可以使用标准的潜变量建模软件进行拟合分析, 例如Mplus、LISREL和Amos等, 这将极大地促进Bi-HM的应用与推广。本文内容结构安排如下：首先回顾van der Linden (2007)的HM; 其次介绍Bi-HM的提出; 然后通过模拟研究评估Bi-HM参数估计效果; 接下来利用实例数据评估模型的拟合效果; 最后进行总结与展望。

2 双因子分层模型

2.1 模型构建

在介绍Bi-HM模型前, 先介绍van der Linden (2007)提出的HM。在HM中, 第一层是作答反应与作答时间模型。作答反应模型为两参数logistic模型, 可以表示为

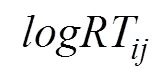
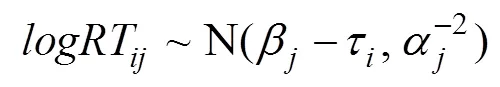
在HM的第二层为被试参数间的相关与项目参数间的相关, 通常假设被试能力特质与速度特质服从二元正态分布, 项目难度相关参数与作答时间强度参数服从二元正态分布, 如式(3)和式(4)所示。

在对测验的作答反应与时间进行分析时, HM仅仅通过被试参数间的关系(式3)和项目参数间的关系(式4)来量化作答时间与反应的关系是不够的(如图1a所示)。Bi-HM将测验的作答时间与反应视为测量被试能力和速度的两个局部因子, 同时测验的作答时间与反应又综合测量了被试的一般潜在特质或全局因子, 以及速度与准确率权衡能力(如图1b所示)。因此, 在借鉴双因子模型思路基础上提出Bi-HM。

图1 分层模型与双因子分层模型示意图

在Bi-HM的第一层模型中, 作答反应模型与作答时间模型分别可以表示为

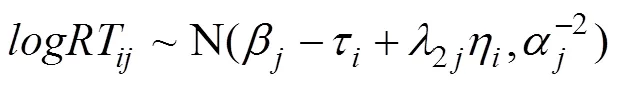
2.2 参数估计与模型识别

3 模拟研究

对模拟研究, 主要基于两个目的展开探究, 其一是不同条件对Bi-HM参数估计的返真性的影响; 其二是忽视作答时间与反应关系对传统分层模型HM所带来的影响。

表1 作答时间与反应的不同关系类型

3.1 评价指标

对于模拟结果采用MSE (Mean squared error)和平均Bias进行评价, MSE和Bias值越小意味参数的估计值与模拟值越接近, 结果越佳。

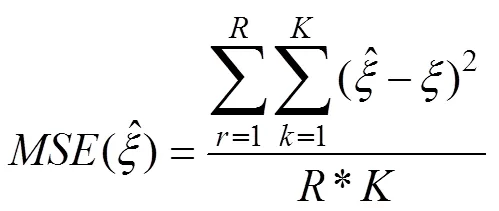
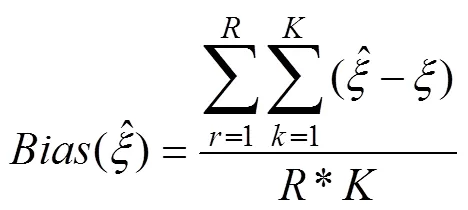
3.2 数据生成与分析

3.3 结果

图2 不同条件HM和Bi-HM项目参数估计效果

注：HM = van der Linden的分层模型; Bi-HM = 双因子分层模型。

图3 不同条件HM和Bi-HM被试参数估计效果

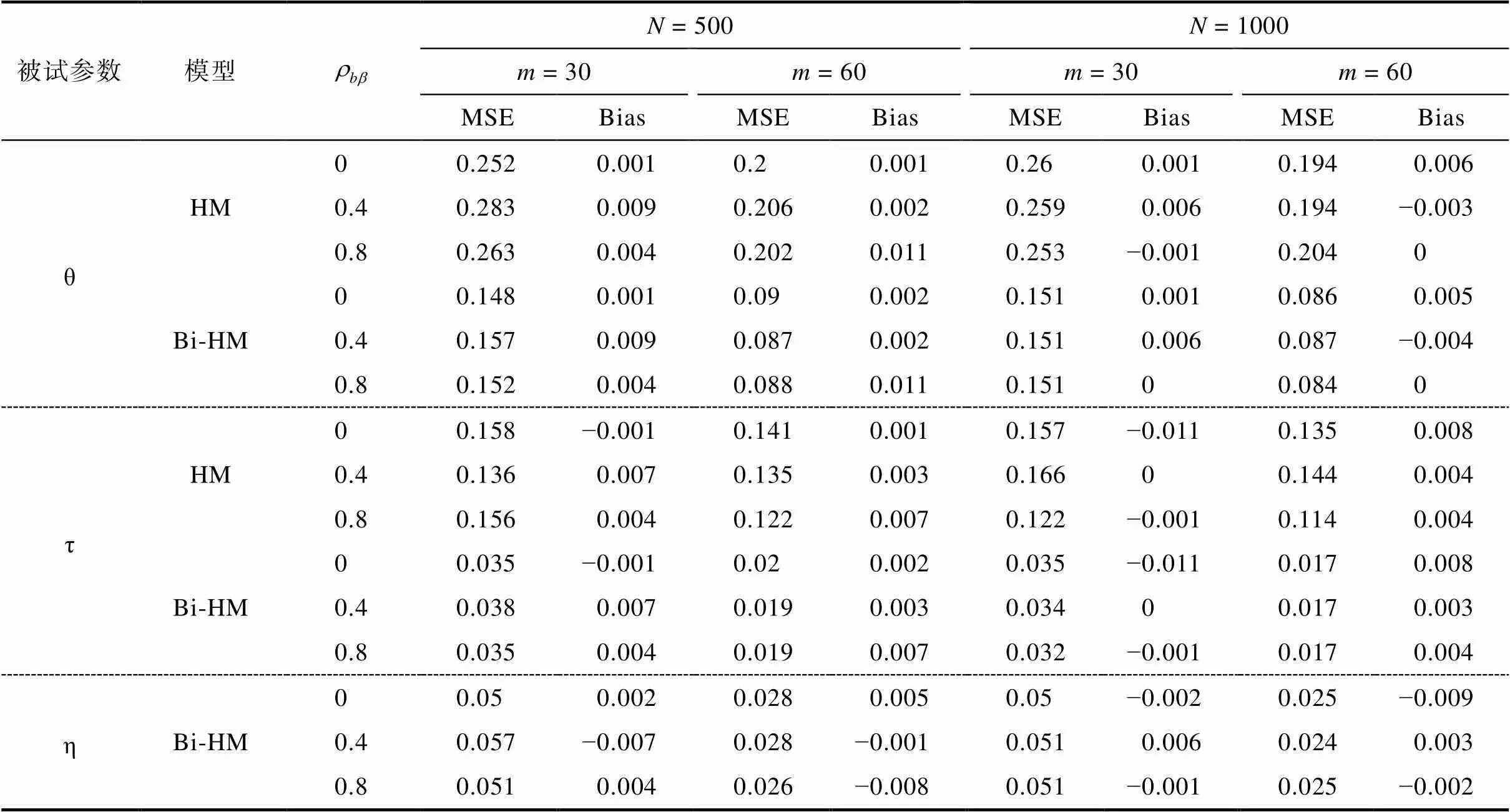
表3 HM与Bi-HM被试参数返真性

注：HM = van der Linden的分层模型; Bi-HM = 双因子分层模型。

4 实例数据分析

4.1 数据描述

通过E-prime 2.0搜集《瑞文标准推理测验》作答数据, 每个项目作答结束后会进入下一个项目, 不能返回修改, 共60个项目, 要求被试在45分钟内完成。该测验共施测427名大学生, 原始作答时间数据均事先进行对数转换。

4.2 分析

4.3 结果

《瑞文标准推理测验》数据的模型拟合结果如表4所示。从表中可以看出, HM的各模型拟合指数AIC、BIC和SABIC要小于Fix-Bi-HM的各拟合指数, 但是明显大于Bi-HM的拟合指数, 同时Bi-HM的LL值最大。这表明固定作答时间与反应的项目水平依赖关系后, Bi-HM拟合急剧变差。同时, Bi-HM更能符合实际数据的特征, 具有更好的拟合效果。

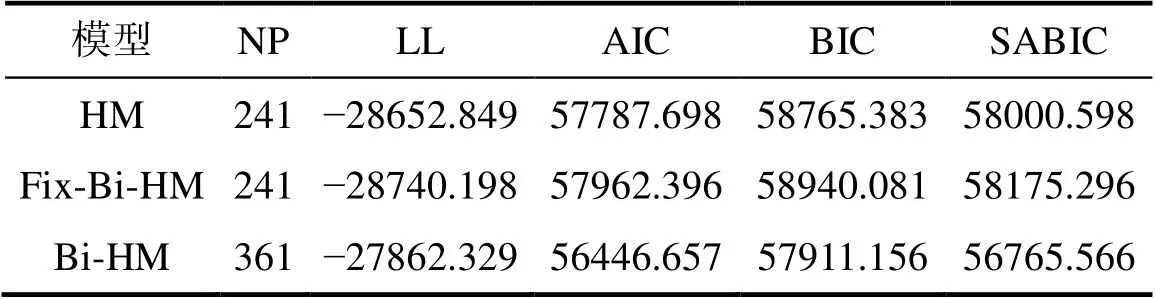
表4 瑞文标准推理测验数据分析中模型-数据拟合指标

注：NP = 自由参数量; LL = Loglikelihood; AIC = Akaike’s information criterion; BIC = Bayesian information criterion; SABIC = Sample-Size Adjusted BIC。

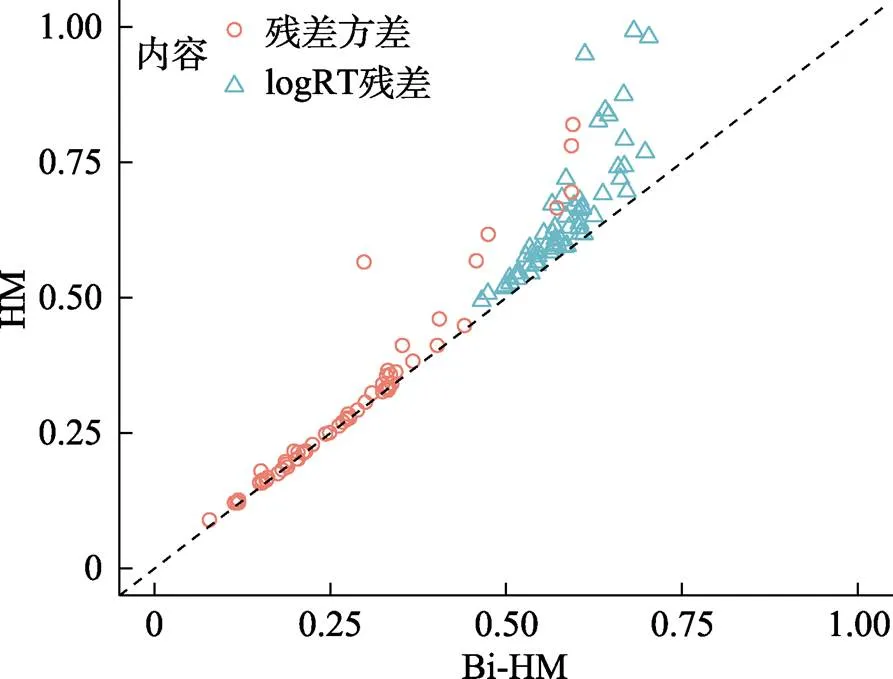
图4 HM和Bi-HM残差比较

图5 Bi-HM项目参数的相关矩阵

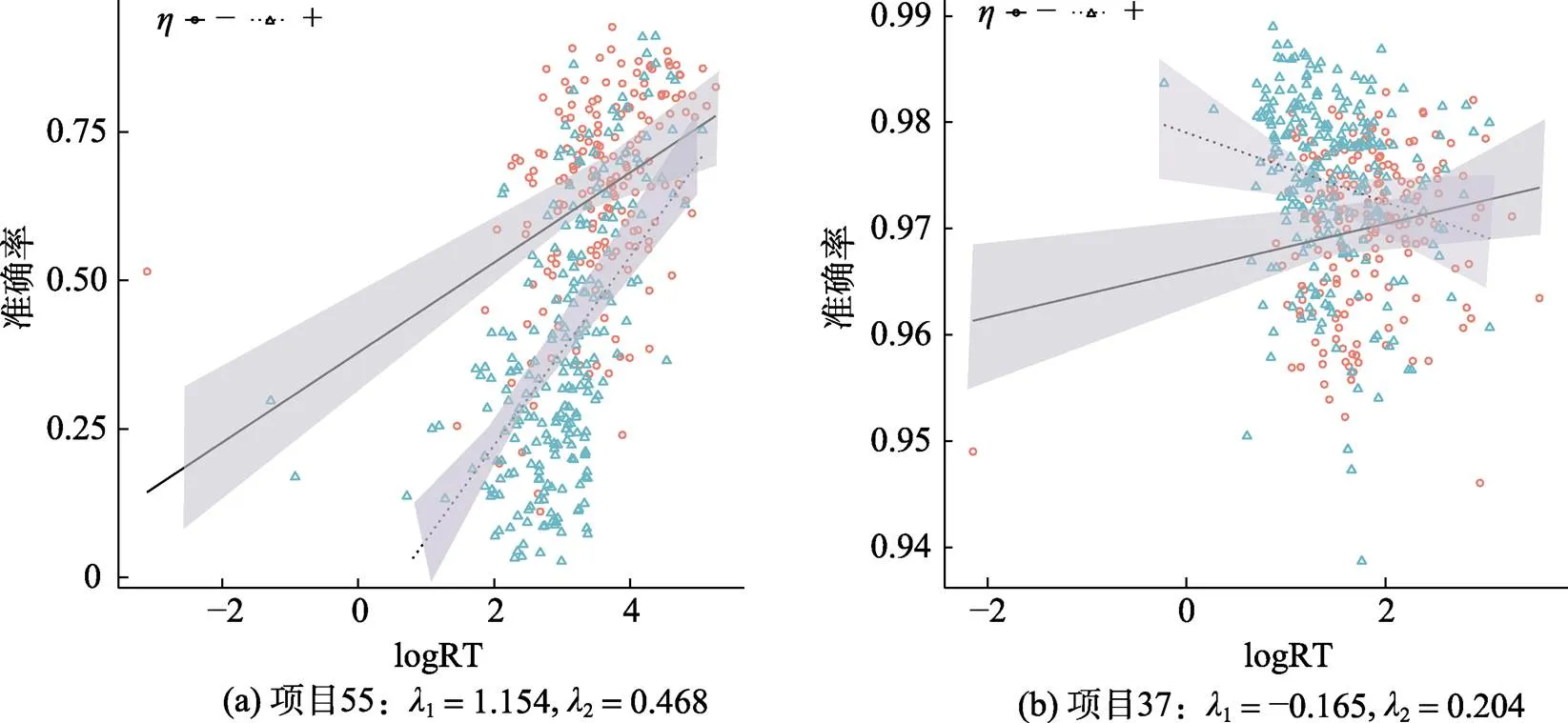
图6 不同类型的作答时间与准确率关系趋势

5 总结和展望

作答时间与反应都反映了被试重要的作答信息, 分层模型(Hierarchical Model, HM)(van der Linden, 2007)的提出为联合分析作答时间与反应提供了基本框架, 并逐渐成为当前最流行的建模方法。然而, HM只通过项目参数间的关系与被试参数间的关系来解释作答时间与反应之间的依赖关系, 这在某种程度上是不够的。虽然不同研究者提出了一系列改进模型, 但仍存在一些局限性(郭小军等, 2019; Bolsinova et al., 2017, 2018; Range et al., 2012)。为了更好地反映作答时间与反应间的依赖关系, 文中从双因子模型视角出发, 将测验的作答时间与反应分别视为测量了被试速度和能力两个局部因子, 而作答时间与反应又综合测量了被试的速度与准确率权衡的一般能力或全局因子, 基于此构建了双因子分层模型(Bifactor hierarchical model, Bi-HM)。Bi-HM能灵活地反映作答时间与反应间的不同关系, 并且可以通过常用的结构方程模型软件对模型参数进行估计, 这对Bi-HM的应用非常有利。模拟研究发现, 基于MLR的Mplus程序能有效估计Bi-HM的各参数, 并且参数估计结果不受项目参数间的相关水平的影响。然而, HM因忽视作答时间与反应间的依赖关系进而导致参数估计结果存在明显偏差。在实例数据中, Bi-HM的模型拟合指数明显优于HM, 并且项目的时间残差和残差方差也明显要小于HM, 这表明考虑作答时间与反应依赖关系的Bi-HM更符合实例数据。同时, 被试在大部分项目上的作答心理主要分为增加时间以提高准确率或牺牲准确率以降低作答时间, 然而部分简单项目也存在增加作答时间后准确率反而下降的现象(郭小军等, 2019; Bolsinova, Tijmstra, & Molenaar, 2017), 这可能是由于被试在测试期间效率发生变化的结果(Chen et al., 2018)。

值得肯定的是研究取得了较好的结果, 但是仍然存在一些局限性需要进一步研究来完善。首先, Bi-HM只对单维测验的作答时间与反应进行了模拟与实证研究, 基于双因子模型的视角探究作答时间与反应的依赖关系可以从多个方面进行拓展。从测验维度上, 可以将Bi-HM从单维测验向多维测验拓展(郭小军等, 2022; 魏丹等, 2017), 构建多维的双因子分层模型, 甚至高阶双因子分层模型; 从过程数据的类型上, 除了作答时间与反应数据外, 还可以向注视点数据(詹沛达, 2022)和鼠标单击/拖动轨迹数据(Liang et al., 2023)等扩展, 此时不同过程数据类型视为测量多个局部或特定因子进行双因子分层模型的构建, 探讨不同过程数据间的相互影响; 从作答时间与反应的依赖关系的形式上, 文中只探讨了线性的关系, 但是也有研究发现有的项目的作答时间与反应之间存在非线性关系(郭小军等, 2019; Bolsinova et al., 2018; Chen et al., 2018), 例如将速度与准确率权衡能力定义为二项式形式。其次, 虽然模拟研究发现未考虑项目参数间关系的Bi-HM的参数可以通过Mplus程序进行有效估计, 但是未来的研究可以比较贝叶斯估计和Mplus的MLR估计结果, 以进一步探究忽视项目参数间相关的影响(Molenaar et al., 2015)。最后, 在作答时间模型的适用性上, 对数正态时间模型可能并不适用所有的时间数据, 因此可以考虑对模型进行不同形式的变换或者选择其他模型来更好地适应作答时间的分布(孟祥斌, 2016; Klein Entink, van der Linden, & Fox, 2009; Wang et al., 2013)。

Bolsinova, M., De Boeck, P., & Tijmstra, J. (2017). Modelling conditional dependence between response time and accuracy.,(4), 1126−1148.

Bolsinova, M., & Molenaar, D. (2018). Modeling nonlinear conditional dependence between response time and accuracy.,, 1525.

Bolsinova, M., & Tijmstra, J. (2016). Posterior predictive checks for conditional independence between response time and accuracy.,(2), 123−145.

Bolsinova, M., Tijmstra, J., & Molenaar, D. (2017). Response moderation models for conditional dependence between response time and response accuracy.,(2), 257−279.

Cai, L., Yang, J. S., & Hansen, M. (2011). Generalized full-information item bifactor analysis.,(3), 221−248.

Chen, H., De Boeck, P., Grady, M., Yang, C.-L., & Waldschmidt, D. (2018). Curvilinear dependency of response accuracy on response time in cognitive tests.,, 16−23.

Davison, M. L., Semmes, R., Huang, L., & Close, C. N. (2012). On the reliability and validity of a numerical reasoning speed dimension derived from response times collected in computerized testing.,(2), 245−263.

Guo, X., & Luo, Z. (2019). The trade-off between speed and accuracy: Evaluation and modeling for participants in the response states.,(5), 589−595.

[郭小军, 罗照盛. (2019). 速度与准确率权衡: 被试反应状态评价与建模.,(5), 589−595.]

Guo, X., Luo, Z., & Yan., J. (2022). Modeling of the effect on multidimensional latent speeds in the between-item multidimensional response time.,(5), 1222−1229.

[郭小军, 罗照盛, 严娟. (2022). 项目间多维测验作答时间数据分析: 潜在特质速度间效应建模.,(5), 1222−1229.]

Guo, X., Luo, Z., & Yu, X. (2020). A speed-accuracy tradeoff hierarchical model based on cognitive experiment.,, 2910.

Klein Entink, R. H., Kuhn, J.-T., Hornke, L. F., & Fox, J.-P. (2009). Evaluating cognitive theory: A joint modeling approach using responses and response times.,(1), 54−75.

Klein Entink, R. H., van der Linden, W. J., & Fox, J.-P. (2009). A box-cox normal model for response times.,(3), 621−640.

Liang, K., Tu, D., & Cai, Y. (2023). Using process data to improve classification accuracy of cognitive diagnosis model.,(5), 969−987.

Loeys, T., Rosseel, Y., & Baten, K. (2011). A joint modeling approach for reaction time and accuracy in psycholinguistic experiments.,(3), 487−503.

Lu, J., Wang, C., & Shi, N. (2021). A mixture response time process model for aberrant behaviors and item nonresponses.,(1), 71−89.

Luce, R. D. (1986).. New York: Oxford University Press.

Mao, X., Xia, M., & Xin, T. (2018). Full-information item bifactor analysis: Model parameter estimation and application.,(2), 358−367.

[毛秀珍, 夏梦连, 辛涛. (2018). 全信息项目双因子分析: 模型、参数估计及其应用.,(2), 358−367.]

Meng, X.-B. (2016). A log-skew-normal model for item response times.,(3), 727−734.

[孟祥斌. (2016). 项目反应时间的对数偏正态模型.,(3), 727−734.]

Meng, X.-B., Tao, J., & Chang, H.-H. (2015). A conditional joint modeling approach for locally dependent item responses and response times.,(1), 1−27.

Molenaar, D., Tuerlinckx, F., & van der Maas, H. L. J. (2015). A generalized linear factor model approach to the hierarchical framework for responses and response times.,(2), 197−219.

Muthén, L. K., & Muthén, B. O. (2019).. Muthén & Muthén.

Scherer, R., Greiff, S., & Hautamäki, J. (2015). Exploring the relation between time on task and ability in complex problem solving.,, 37−50.

van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items.,(3), 287−308.

van der Linden, W. J. (2009). Conceptual issues in response- time modeling.,(3), 247−272.

van der Linden, W. J., & Glas, C. A. W. (2010). Statistical tests for conditional independence in a hierarchical model for speed and accuracy on test items.,(1), 120−139.

Wang, C., Chang, H.-H., & Douglas, J. A. (2013). The linear transformation model with frailties for the analysis of item response times.,(1), 144−168.

Wei, D., Liu, H., & Zhang, D. (2017). Multidimentional rasch testlet model: An extension and generalization of MRCMLM.,(12), 1604−1614.

[魏丹, 刘红云, 张丹慧. (2017). 多维题组反应模型：多维随机系数多项Logistic模型的应用拓展.,(12), 1604−1614.]

Ranger, J. (2013). Modeling responses and response times in personality tests with rating scales.,(4), 361−382.

Ranger, J., & Ortner, T. (2012). The case of dependency of responses and response times: A modeling approach based on standard latent trait models.,(2), 128−148.

Zhan, P. (2022). Joint-cross-loading multimodal cognitive diagnostic modeling incorporating visual fixation counts.,(11), 1416−1423.

[詹沛达. (2022). 引入眼动注视点的联合-交叉负载多模态认知诊断建模.,(11), 1416−1423.]

Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times.,(2), 262−286.

Zhan, P., Wang, W.-C., & Wang, L. (2013). Testlet response theory: An introduction and new developments.,(12), 2265−2280.

[詹沛达, 王文中, 王立君. (2013). 项目反应理论新进展之题组反应理论.,(12), 2265−2280.]

Zheng, C.-J., Guo, C.-Y., & Bian, Y.-F. (2011). Using testlet DIF procedures to detect testlet DIF in chinese passage-based reading testing.,(7), 830−835.

[郑蝉金, 郭聪颖, 边玉芳. (2011). 变通的题组项目功能差异检验方法在篇章阅读测验中的应用.,(7), 830−835.]

Modeling the dependence between response and response time: A bifactor model approach

GUO Xiaojun1, BAI Xiaoyun1, LUO Zhaosheng2

(1School of Education Science / Center for Education and Economic Research, Gannan Normal University, Ganzhou 341000, China)(2School of psychology, Jiangxi Normal University, Nanchang 330022, China)

In the realms of psychological and educational testing, the computerization of tests is becoming more prevalent, facilitating the acquisition of process data from test-takers. In the domain of process data, response time and response represent the two most commonly utilized variables. Responses provide critical insights into the answers provided by test-takers, while response time, as an essential source of information, is increasingly garnering attention from researchers. The proposal of hierarchical model (HM) has provided a fundamental modeling framework for the joint analysis of response time and response, and it is becoming increasingly popular in current research practices. However, relying solely on the association between item and subject parameters is insufficient to adequately explain the correlation between response time and response. Consequently, researchers have proposed various enhanced models to address these limitations, although some challenges persist.

The bifactor model explains common variance through a general or global factor, while a local or specific factor explains the common variance of additional partial items. In psychological and educational testing, it is possible to capture not only the test-takers’ response times on test items but also their responses. From the perspective of the bifactor model, response times and responses to test items measure different local factors. Specifically, a test's response time measures the test-taker's speed trait, while the response to the test measures their ability trait. Test-takers are also influenced by a combination of time and accuracy when responding to the test, known as general latent traits or global factors, or speed-accuracy trade-off ability. This test structure aligns well with the bifactor model and provides a new perspective on analyzing the relationship between test-taking response time and response dependence. Based on this, this study proposes a bifactor hierarchical model (Bi-HM) to explore the dependency between response time and response.

In the simulation study, it was found that the MPLUS program utilizing MLR (Maximum Likelihood Robust), could accurately estimate the parameters of the Bi-HM and was not influenced by the level of item parameter correlation. Conversely, when disregarding the relationship between response time and response in the HM, notable bias in the parameter estimates occured. In the empirical data analysis, the Bi-HM demonstrated significantly superior model fit indices compared to the HM. Moreover, the Bi-HM effectively captured the dependency between response and response time at both the participant and item levels. This dependency is closely associated with item difficulty and time intensity factors.

Based on the findings mentioned above, it is evident that the Bi-HM, which adopts a bifactor model perspective, excels in parameter estimation and data fitting, demonstrating excellent scalability.

response time, response, dependency relationship, hierarchical model, bifactor model

2023-06-27

* 江西省社会科学“十四五”基金项目(21JY49)、江西省教育厅科学技术研究项目(GJJ2201241)资助。

罗照盛, E-mail: luozs@126.com

B841