安时积分法和EKF 结合的锂电池SOC 估计

龙振弘

（三明教育学院信息技术处，福建 三明，365000）

1 引言

准确的电池荷电状态（State of Charge,SOC）[1]估计可以推测出电动汽车的续航里程，消除驾驶员的“里程焦虑”，同时为电动汽车的能量管理、寿命监测、电池均衡等提供准确的判断依据，因此成为电动汽车发展的热点问题。SOC 估计精度是当前电池管理系统的研究重点，且存在有待进一步改进和提高的方面[2]。目前SOC 估计常见方法有安时积分法、阻抗分析法、开路电压法等。近年来出现了基于卡尔曼滤波类方法、机器学习类方法、非线性观测器类方法等[3]，以及基于上述几类方法的改进或融合，用以提高SOC 估计精度[4-8]。当前国内外研究的SOC 估计方法均能够有效估计SOC 并达到一定精度，但是存在算法复杂度和精度之间的矛盾、时间或电流累计误差、依赖模型准确度以及实际应用下的工程实现等问题。为提高SOC 的估计精度，从工程实际出发，提出一种采用安时积分法和扩展卡尔曼滤波法相结合的方法，以较少的计算资源达到较高的估计精度。

2 电池建模及参数辨识

电池使用过程中的外特性与RC 网络特性具有相似性，RC 网络能够较好地模拟电池的极化效应。戴维南（Thevenin）等效模型使用若干RC 并联网络结合线性模型来近似电池特性，RC 网络阶数越高，对极化特性的反映越精确。戴维南等效模型可以根据系统要求和资源灵活选用阶数，能够适应不同精度和复杂度的要求。为能较好地兼顾精度和复杂度，此处采用一阶戴维南等效模型，其结构如图1 所示。

图1 一阶戴维南等效电路模型

通过复合脉冲电池放电试验（Hybrid Pulse Power Characterization,HPPC），以串联电池组的充放电电流为输入，端电压为电池系统的输出，对电池的周期性充放电响应特性进行分析，由此计算出电池模型中各元件的参数。

脉冲放电过程为：以1/3 C 放电10 s，然后静置30s，最小采样间隔为0.1s，采集此SOC 下电压变化曲线。HPPC 过程电池端电压随电流的变化曲线如图2 所示。单次脉冲放电曲线如图3 所示。

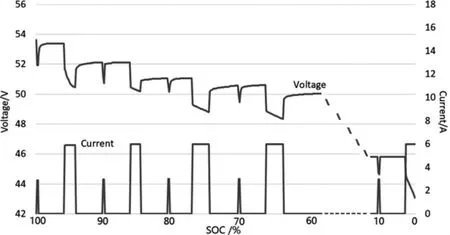
图2 HPPC 过程电压变化曲线

图3 单次脉冲放电曲线示意图

在t1时刻开始放电，工作电压会有明显的陡然下降。根据一阶戴维南等效电路模型可知电压陡降数值与电流比值为等效内阻R0，即：

在t2时刻，电池停止放电，电池等效内阻不再分压。之后到U4到U5阶段，是容阻回路的零输入响应阶段。由于RC 回路的存在，充满电的等效极化电容CP开始对等效极化内阻RP放电，在外特性中呈现为电池端电压缓慢上升；当等效极化电容两极板上电荷全部释放后时，电池的端电压不再发生变化，此时测得的电池端电压即为电池开路电压。

由基尔霍夫电流定律，可得：

式中，UP是电容电压；UR是电阻两端电压。对式(2)求解，可得：

式(3)为容阻回路零输入响应，表示U4到U5时刻电压的变化趋势。其中，τt 为时间常数；A 为电容初始电压；Δt 为采样时间，其中τt=RPCP。

t1到t2时刻为放电过程，由基尔霍夫电流定律，可得：

式(4)为一阶常系数线性非齐次微分方程，其通解为：

式中，可用最小二乘法求解出RP的值，然后根据τt=RPCP可求出CP的值。

图1 的RC 环路的零输入和零状态响应为：

根据基尔霍夫电压定律可得到电池端电压UL、等效电容电压UP的参数关系式：

模型参数辨识结果如表1 所示。

表1 模型参数辨识结果

通过HPPC 试验所辨识出的SOC-OCV 曲线以及不同SOC 时刻的内阻R0、极化电容CP和极化电阻RP的值，拟合后可得到SOC 和R0、RP、CP的函数关系。至此，利用安时积分法和EFK 的进行SOC 估算所需的参数已全部得出。

3 安时积分法与EFK 的SOC 估计

3.1 安时积分法

安时积分法是通过对放电电流或充电电流进行实时监测，并在时间上进行积分以获得电池充放电电量，最终结合初始电量及电池总电量计算出SOC。计算公式如下式：

其中，SOC(t0)表示估计方法开始时SOC 的初始值，SOC(t)表示t 时刻SOC 的估计值；QI为电池额定电量；I 为充放电电流。其增量表达式为：

式中，ki为经验修正系数，通过不同恒流值放电试验获取。

安时积分法需要获取电池的初始SOC、实时电流及采样时间间隔。在工程实际中，电池初始值一般由开路电压法、外部存储初值或满电状态进行初始化。安时积分法容易产生累计误差[9]，需要适时纠正。实时电流的准确性是安时积分法结果精确性的关键，采样时间间隔有两方面的要求，一方面时间间隔要尽量小，避免遗漏电池组电流的瞬时变化的获取；另一方面采样间隔要参与积分运算，因此其数值要非常精确。

3.2 扩展卡尔曼滤波

卡尔曼滤波方法是最优估计理论中最为广泛应用和研究的方法之一。传统的卡尔曼滤波方法是建立系统的状态方程及观测方程，通过对状态变量和先验均方误差进行预测，再根据测量值对预测值进行修正，最终估计出更加精确的系统状态变量值，不适用于非线性系统。电动汽车动力电池组的系统模型是一个非线性系统，电池SOC 值和实时电流、端电压、温度、电池健康程度等多个参数间呈现复杂的非线性关系。卡尔曼滤波算法的性能严重依赖于电池系统模型建立的准确性，当电池系统模型发生变化时，算法会发生不稳定甚至失效现象[10]。扩展卡尔曼滤波算法（Extended Kalman Filter,EKF）与传统卡尔曼滤波算法的区别在于前者的模型建立可以是非线性的，即其系统状态方程和观测方程为非线性表达式，通过对非线性系统数学模型进行泰勒级数展开，按照精度要求取前若干项构成一个近似于原系统的线性系统，再使用传统卡尔曼滤波算法进行最优估计。然而扩展卡尔曼滤波算法复杂度较高，计算量较大，对硬件资源要求较高。因此在工程实现过程中，需要兼顾建立精确的系统模型及降低运算时间，以保证估计算法的精确性和实时性。

扩展卡尔曼滤波的状态方程和观测方程如下：

和传统卡尔曼滤波算法相比，仅考虑At、Bt和Ct的区别。由此可得到扩展卡尔曼滤波算法流程图，如图4 所示。

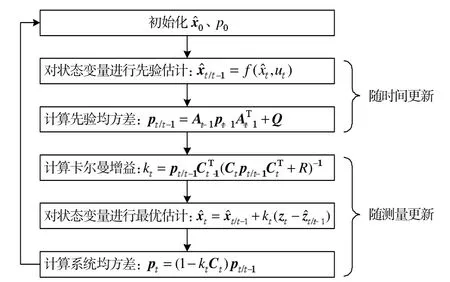
图4 扩展卡尔曼滤波算法流程图

以SOC 和UP为状态变量，以端电压UL为可观察输出变量，按照EKF 算法建立电池组等效模型的状态方程和观测方程：

则卡尔曼滤波计算所需矩阵Xt、At、Bt和Ct为：

根据SOC 和R0、RP、CP的拟合关系，每次迭代时求出At-1、Bt-1的值；根据OCV-SOC 曲线拟合关系得到每次迭代时Ct的值。通过图4 流程图即可实现基于一阶戴维南等效模型的EFK 的SOC 估计算法。

4 SOC 估计程序

4.1 C 语言矩阵运算

因EKF 算法每次迭代会产生大量的临时矩阵，但单片机系统存储空间有限，且缺少内存管理，故采用二级指针数组实现矩阵存储，可在一定程度避免内存错误。二级指针数组的存储原理如图5 所示。

图5 二级指针存储原理图

第一级指针为double** 类型，指向的地址为double*数组的首地址，此数组代表矩阵每行的首地址；每个double*类型的指针又指向一个double 类型数组的首地址，此数组存储矩阵中的一行数据，数组长度为矩阵列数。

4.2 计算资源利用

计算资源利用，需要对内存进行动态分配和回收及调节堆栈大小，为单次算法迭代提供充足内存空间。将EKF 每次迭代分为五个程序部分以实现平稳运行：①状态变量先验估计；②先验均方差计算；③卡尔曼增益计算；④状态变量后验估计；⑤均方误差计算。每部分进行完毕后，保留下一部分所需矩阵数据，并回收此部分中间计算产生的其他矩阵，以实现在BMS 系统内每0.5s 内运行一次算法迭代。

4.3 程序流程

EFK 算法需要占用较多的计算资源和内存空间，且其收敛到精确值需要若干次迭代计算。因此，在系统空闲时段，启动EFK 算法对SOC 值进行估计；在系统繁忙时段，例如电池均衡、通信功能或热处理功能启动时，停用EFK 算法，并以停用时的SOC 估计值作为初值启用安时积分法。在BMS 系统工作时，系统空闲时段和繁忙时段通常交替进行，安时积分法产生积累误差会在空闲时段进行EFK 估计时得以消除；同时，此切换设计也会给予卡尔曼滤波法充足的计算资源，使其正常运行。此外，当充电电流过小或单体电池平均开路电压达到4.2V 时判定电池充满。SOC 估计程序流程如图6 所示。

图6 SOC 估计程序流程

5 实验验证与分析

实验设备为：新威CT4008 电池分析仪；嵌入式电池管理系统（Battery Manage System,BMS）；四节18650 锂电池串联（单体电池容量2400mAh）。

使用电池分析仪对电池组2A 恒流放电，以电池分析仪显示SOC 为实测值。每3 分钟记录一次SOC 实测值，放电过程中通过电池管理平台对电池组进行SOC 估计。SOC 估计程序设置为安时积分法加以间隔进行的EKF 估计算法。如图7 所示是SOC放电时的SOC 实验结果。

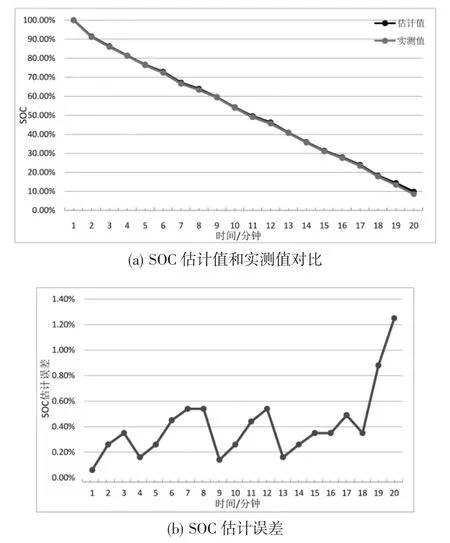
图7 SOC 放电时的SOC 实验结果

实验以放电过程中电池分析仪检测的SOC 实测值为真实值，以嵌入式电池管理系统运行所提的估计算法得到结果为估计值进行对比。如图7(a)所示，当锂电池的剩余电量接近10%时，由于锂电池开路电压变化剧烈，因此估计误差最大，约为1.25%。如图7(b)所示：安时积分法运行时的SOC 估计误差逐渐扩大，切换到EKF 估算后，SOC 估计误差收敛到真值附近。在整个放电过程中，SOC 估计的平均误差约0.4%，可以满足电动汽车SOC 估计的精度要求。

6 结束语

用安时积分法和EKF 相结合，进行SOC 估计，针对的是在使用安时积分法时由于运算周期误差和电流采样误差容易产生累计误差，导致SOC 估计误差有逐渐扩大的趋势。采取EKF 估计算法后，将累计误差修正，SOC 估计精度得到提高。研究结果表明所提出的SOC 估计算法，既有较高的估计精度，又可以减少计算资源，因此具有良好的工程应用价值。在未来的后续研究中，还有一些提高估计精度的思路有待实现：将温度加入模型参量，辨识出各个温度下的等效电池模型并拟合，在算法迭代计算时适时考虑模型参数的变化；建立高阶、更复杂的电路等效模型，以某参量为坐标在电池整个生命周期的不同坐标对电路模型进行建模等。上述方法均使用变化的模型而不是固定模型以提高精度，但是需要更强大的硬件计算能力。