多阶段屈服U形金属阻尼器抗震性能研究

王德斌,王英豪,赵汉涛

(1.大连交通大学 土木工程学院,辽宁 大连 116028; 2.中建一局集团建设发展有限公司,北京 100102)

现有消能减震结构往往通过附加耗能构件耗散地震输入的大部分能量,该方法能够有效降低主体结构的地震响应和损伤。金属阻尼器以其力学模型简单、滞回性能稳定、抗疲劳性能良好、制造安装方便等优势,在实际工程中得到广泛应用和推广[1]。

金属阻尼器能够为结构提供附加刚度和阻尼,有效降低结构在地震荷载作用下的位移响应。Zibasokhan等[2]提出了一种纯弯曲变形金属阻尼器,该阻尼器具有稳定的滞回、变形性能,耗能能力优异。Deng等[3]提出了设置加劲板的剪切型金属阻尼器,该阻尼器能够在低位移水平下实现剪切耗能,加劲板的设置提升了阻尼器的防屈曲能力,耗能能力得到显著提高。王德斌等[4]基于扭转变形机制提出了一种具有多截面屈服,应力、应变分布均匀的新型扭转钢管阻尼器,将其应用于支撑钢框架,展示了较好的减震控制效果。程扬等[5]将矩形剪切钢板与U形钢板进行并联组合,提出了一种具有多阶段屈服特点的金属阻尼器,该阻尼器能够在不同强度的地震作用下实现分阶段屈服的耗能目标。吴山等[6]采用不同尺寸的钢条作为耗能构件,提出了具有多阶段屈服和失效特性的金属套管阻尼器。

目前金属阻尼器在研究和应用中仍存在以下问题:①现有金属阻尼器往往针对中大震进行性能设计,难以在低位移水平下的弹性状态实现耗能[7-8];②部分剪切型金属阻尼器虽能在低位移水平下实现屈服耗能,高位移水平下则强度退化明显,难以达到结构更高的耗能需求;③单一破坏阶段的金属阻尼器,耗能组件发生破坏后,阻尼器迅速失效,无法满足后续地震作用下结构的耗能需求[9]。

基于上述分析,本文提出了一种具有多阶段屈服和失效特点的U形金属阻尼器。给出了该阻尼器的基本构造、工作机理和恢复力模型,采用Abaqus软件对其滞回性能、耗能能力和破坏过程进行了分析,通过对比有限元模拟结果和恢复力模型,验证了恢复力模型的准确性。

1 阻尼器基本构造和理论模型

1.1 基本构造和工作机理

本文设计的多阶段屈服U形金属阻尼器构造见图1。该阻尼器由具有不同尺寸参数的上下和前后对称布置的U形耗能钢板及内部加载轴杆、外部约束套筒所组成,U形钢板中部截取部分平直段长度,采用焊接的形式固结于约束套筒和加载轴杆之上。U形钢板在外荷载作用下发生滚动弯曲变形并进行屈服耗能,其屈服截面随位移的变化不断移动,形成多截面屈服的变形特点,能够有效提升耗能钢板的抗疲劳性能。

(a) 阻尼器整体构造

阻尼器尺寸参数见图2。通过调整阻尼器U形钢板A、B的尺寸,实现低位移水平下U形钢板A率先发生屈服,此时阻尼器的受力和耗能主要由U形钢板A承担。在高位移水平下U形钢板A发生破坏,承载能力和耗能能力下降,此时U形钢板B发生屈服,并充分发挥其变形能力强、抗疲劳性能好的优势,完成后续承载工作。

(a) 侧视图

本文共设计3种阻尼器工况,试件1仅对称布置U形钢板A,试件2仅对称布置U形钢板B,试件3则由试件1和2组合,前后和上下分别对称布置U形钢板A和B,进而实现多阶段屈服耗能,各工况下试件的具体尺寸参数见表1。

表1 阻尼器U形钢板尺寸参数 mm

1.2 恢复力模型

阻尼器的屈服荷载、初始刚度、屈服后刚度和极限荷载作为阻尼器的重要力学性能指标,对其理论恢复力模型的建立极其重要。本文单个双U形阻尼器的全截面屈服荷载Fy、初始刚度K1和屈服后刚度K2、等效屈服位移δy、极限荷载Fu表达式[10]为:

(1)

(2)

K2=αK1

(3)

(4)

Fu=βFy

(5)

式中:ω为U形钢板宽度;σy为U形钢板材料屈服强度;t为U形钢板厚度;d为U形钢板圆弧段内侧直径;μ为初始刚度修正系数;E为材料弹性模量;α为双U形钢板屈服后刚度与初始刚度之比;β为双U形钢板极限荷载与屈服荷载之比。

以阻尼器受拉时的荷载-位移曲线和刚度变化为例,其在不同加载阶段的力学模型见图3。阻尼器各加载阶段下两组U形钢板的变形相同,U形钢板A和U形钢板B属并联关系, 其力学模型是由两者力学性能指标的线性叠加所组成。阻尼器刚度的变化主要经历三个不同的受力阶段。

OA段,阻尼器开始加载至U形钢板A屈服前,此时0<δ≤δy1。U形钢板B并未发生屈服,其刚度和承载力计算表达式为:

δy1=δyA,K1=2(K1A+K1B),F=K1δ

(6)

Fy1=FyA+K1BδyA

(7)

AB段,阻尼器U形钢板A屈服后至U形钢板B屈服前,此时δy1<δ≤δy2。阻尼器刚度和承载力计算表达式为:

δy2=δyB,K2=2(K2A+K1B),F=K2δ

(8)

Fy2=Fy1+K2(δyB-δyA)

(9)

BC段,阻尼器U形钢板B屈服后直至加载至最大荷载Fmax之前,此时δy2<δ≤δmax。阻尼器刚度和承载力计算表达式为:

K3=2(K2A+K2B),F=K3δ

(10)

2 阻尼器有限元模型

本文基于Abaqus软件建立阻尼器有限元模型,约束套筒在不影响阻尼器力学性能的情况下采用一体式建模,阻尼器各部件均采用八节点线性六面体减缩积分实体单元(C3D8R),U形钢板A和B与加载轴杆、约束套筒均采用Tie绑定连接,加载轴杆受力端建立参考点RF并与其端部进行刚体耦合,位移荷载施加于参考点RF之上,初始加载幅值为5 mm,并以5 mm作为位移增量,直至加载至40 mm完成加载,各级幅值均往复循环加载两周。约束套筒、加载轴杆单元尺寸为20 mm,U形钢板单元尺寸细化取5 mm。阻尼器有限元模型见图4。

图4 阻尼器有限元模型

阻尼器有限元模型中,加载轴杆、外部约束套筒采用Q345钢,整个加载过程中始终处于线弹性状态。U形耗能钢板采用Q235级钢,屈服强度σy为235 MPa,弹性模量E为206 GPa,泊松比ν为0.3,采用随动强化本构模型,强化阶段弹性模量为0.01E。

3 模拟结果分析

3.1 滞回性能

各工况下阻尼器滞回曲线见图5,各试件滞回曲线饱满、稳定。从图5可以看出,试件1和2的屈服位移和极限位移均存在一定差异,试件1屈服位移较低,随着位移的增大其变形已由滚动弯曲屈服转换为拉伸变形, 承载力显著提高, 即将发生拉伸破坏,限于软件中材料难以反映阻尼器下降段特征,依据其变形发展趋势可判定试件1总体变形破坏过程。而试件2不论在高位移还是低位移下均展现出了稳定的变形性能,并未出现明显的承载力提升现象,仍处于滚动弯曲屈服状态,高位移水平下展现出稳定的变形能力和耗能能力。

(a) 试件1

试件3滞回曲线则结合试件1和2两者的力学性能差异,承载力值为试件1和2之和,其能够实现低位移水平下的屈服耗能,又能确保高位移水平下具有一定的变形和耗能能力,满足结构的大变形需求。同时从曲线可以看出,在加载后期阻尼器承载力显著提升,可见该阻尼器不仅能够满足高位移水平下的耗能需求,又能依靠基于弯曲变形向拉伸变形转换的U形耗能钢板满足大震下结构更高的承载力需求。

3.2 耗能性能

等效黏滞阻尼比是构件耗能能力的重要评价指标,图6给出了不同工况下试件的等效阻尼比随位移幅值的变化曲线。可以看出,各试件的等效黏滞阻尼比在加载初期迅速增大,加载后期则展现出不同的变化特征。试件1在加载后期等效黏滞阻尼比迅速下降,耗能能力明显降低,其原因主要是随着变形的增大U形钢板变形由弯曲向拉伸转换进而受拉破坏,耗能能力显著降低。而试件2具有较强的变形能力,在加载后期并未发生明显破坏,其等效黏滞阻尼比下降速度平稳,仍能有效吸收外部能量。试件3的等效黏滞阻尼比变化特征介于试件1和2之间,同时具备两者的变形、耗能优势,既能在低位移水平下完成高耗能,又能确保在大位移下仍具备良好的耗能能力。

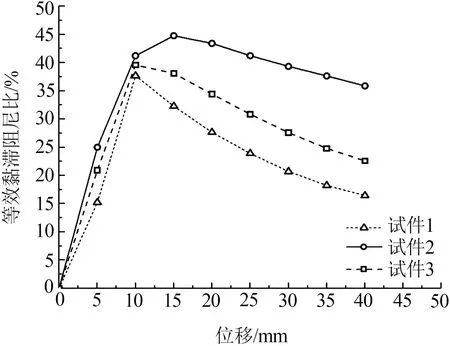
图6 不同工况下试件的等效阻尼比随位移幅值的变化曲线

3.3 破坏过程

图7给出了试件3在位移幅值下U形钢板的等效塑性应变云图。可以看出,塑性应变主要发生在U形钢板平直段和圆弧过渡段。在加载至δ=5 mm幅值时,U形钢板A已展现出显著的塑性变形,而U形钢板B屈服区域极其有限,等效塑性应变值较低。随着位移幅值的进一步增大,U形钢板A的屈服区域明显向弧形板一侧延伸,塑性变形区域明显增加,多个截面均处于高塑性变形区,此时U形钢板B塑性变形区域同样进一步扩展。在δ=20 mm时,U形钢板A已出现由弯曲屈服向受拉变形转换,形成整截面屈服的变化趋势,而U形钢板B仍具有显著变形能力,其U形板上下表面并未发生屈服,可见其能够满足结构的大变形需求,进而使阻尼器能够实现多阶段屈服耗能。

(a) δ=5 mm

4 恢复力模型验证

图8给出了试件3数值模拟和理论力学模型的荷载-位移滞回曲线和骨架曲线的对比结果。可以看出,理论力学模型给出的三折线模型与数值模拟得到的荷载-位移滞回曲线基本吻合,验证了理论力学模型的准确性。阻尼器设计过程中,可以针对不同结构的抗震设计需求,依据本文给出的不同加载阶段的直线表达式实现不同地震强度下阻尼器的承载力、刚度和变形设计要求。

图8 阻尼器模拟和理论模型结果对比

5 结论

本文基于U形钢板的力学性能特点提出了一种多阶段屈服金属阻尼器,给出了其三折线力学模型,通过数值模拟研究了阻尼器的主要力学性能,得到以下结论:

(1)该多阶段屈服金属阻尼器由2种不同尺寸参数的双U形钢板并联而成,能够在不同强度下进行分阶段屈服耗能,实现多级设防水准下的结构抗震理念;阻尼器滞回曲线饱满,具有良好的耗能能力。

(2)低位移水平下高承载力U形钢板率先发生屈服并进行耗能,其塑性变形区域扩展迅速,高位移水平下其变形机制由弯曲转变为拉伸并发生破坏,此时低承载力U形钢板作为主要耗能部件进行耗能。

(3)两类U形钢板在低位移水平下等效黏滞阻尼比均迅速增大,随着位移的增大低承载力U形钢板等效黏滞阻尼比迅速减小,耗能能力降低,而高承载力U形钢板的等效黏滞阻尼比平稳下降,具有更加稳定的耗能能力。

(4)基于Abaqus软件建立了阻尼器有限元模型,模拟得到滞回曲线与给出的分阶段三折线力学模型基本吻合,该力学模型能够很好地反映阻尼器的主要性能指标,可依据结构的不同强度设计要求完成阻尼器的尺寸参数设计。