基于复杂振动载荷的高速列车齿轮箱体强度分析

尹晓亮,范军,杨集友,曹磊,王明萌,赵晓丹,曾迎,张英波

(1.中车长春轨道客车股份有限公司,吉林 长春 130062;2.西南交通大学 材料先进技术教育部重点实验室,四川 成都 610031)

传动齿轮箱是轨道车辆走行部的重要零部件,其结构振动特性和疲劳性能受到广泛关注。随着铁路高速化和轻量化的发展,以及新一代CR450高速列车的投产与试运行,齿轮箱体承受的载荷条件变得更为复杂苛刻[1]。高速列车齿轮箱体不仅要承受电机扭矩载荷,还要承受轮轴传递的因线路激扰引起的振动载荷,由此导致的齿轮箱体失效将严重影响行车安全,故其安全性、可靠性、稳定性对高速列车的安全运营至关重要[2]。目前国内外对高速列车齿轮箱体的强度分析大多仅考虑电机的扭矩载荷[3-6],部分研究在分析箱体疲劳强度时虽然也考虑了振动载荷,但对工况组合进行了简化,存在遗漏最危险条件的可能[7-8]。因此,本文在考虑振动载荷的基础上[9-10],根据不同的工况组合对某车型高速列车齿轮箱体进行静强度和疲劳强度分析,并对分析结果进行评定。

1 动力转向架齿轮箱体结构

本文齿轮箱采用一级圆柱渐开线斜齿轮传动。齿轮箱体是由上箱体和下箱体组成的分体式结构,见图1。齿轮箱体输入端通过联轴器与牵引电机连接,输出端与车轴通过过盈方式连接。齿轮箱体的主要技术参数见表1。

表1 齿轮箱体主要技术参数

图1 齿轮箱体结构

2 齿轮箱体载荷工况及有限元模型

高速列车运行有牵引加速、惰力、制动减速和短路4种工况,在不同工况下齿轮箱体承受的载荷种类不同。

短路工况下齿轮箱体所受载荷为超常载荷,该载荷是一种在整个服役周期内很少出现却可能发生的极限载荷,齿轮箱体结构必须能够承受这种载荷的作用,且不发生永久变形。

在牵引加速、惰行和制动减速3种工况下齿轮箱体承受的载荷是正常运行条件下出现的运营载荷,要求齿轮箱体结构在其设计寿命周期内可承受这种载荷,且不发生疲劳失效。由于3种工况均为运营载荷,故可选择其中最恶劣的一种工况进行疲劳强度校核。

齿轮箱体在动力传递系统中,既要承受牵引和制动工况下的扭矩作用,又要承受来自轮轴传递的线路激扰作用,参照BS EN 13749: 2021中D.2.3对齿轮箱体技术参数的要求[11],可确定齿轮箱体的超常振动载荷和正常运营振动载荷,见表2。

表2 振动载荷参数

高速列车正常运行时,齿轮箱体承受的不同方向线路激扰(载荷)是随机组合出现的,为保证静强度及疲劳强度分析结果的可靠性,确定电机正转和反转短路扭矩时为最恶劣工况,在此工况下考虑纵向、横向以及垂向载荷的16种组合工况进行分析,疲劳强度计算工况采用最大启动扭矩和最大制动扭矩中较大值进行考核,见表3、表4。

表3 静强度计算载荷工况

表4 疲劳强度计算载荷工况

本文在Ansys平台上建立了齿轮箱体的有限元模型。上下齿轮箱体结构有限元模型见图2。整个齿轮箱体强度分析的有限元模型由306 645个节点、1 399 886个四节点四面体单元Solid92、12个Beam单元、2个质量单元和6 335个接触对单元组成。

图2 齿轮箱体结构有限元模型

为了准确模拟齿轮箱体在转向架运行过程中的受力状态,在齿轮箱体结构有限元模型中,齿轮箱体与端盖的结合面、滚动轴承与齿轮箱体和端盖的结合面、螺栓头部与齿轮箱体和端盖的结合面、齿轮轴与齿轮箱体的接触面均用接触对模拟,而简化模型的质量用质量单元进行模拟。

3 齿轮箱体静强度分析

3.1 静强度评定方法

齿轮箱体选用材料为球墨铸铁QT400-18L,其机械性能如下:抗拉强度σb为400 MPa;屈服强度σ0.2为230 MPa;弹性模量E为169 GPa;泊松比μ为0.275;密度为7.3 g/cm3。

根据UIC 615-1: 2003,齿轮箱体结构在最大超常载荷作用下,其静强度条件为结构的最大Von_Mises应力不大于材料的弹性屈服极限,即:σVon_Mises≤σ0.2

3.2 计算结果与分析

对表3中的16种工况分别进行计算。每种工况下齿轮箱体的最大Von_Mises应力和安全系数见表5。在所有工况下,齿轮箱体在工况4时所产生的应力最大,为196.68 MPa,应力最大值出现在上箱体齿面观察窗附近,其安全系数为1.17,应力分布见图3、图4。各工况下的应力值均小于材料的弹性屈服极限230 MPa,故箱体的静强度满足要求。

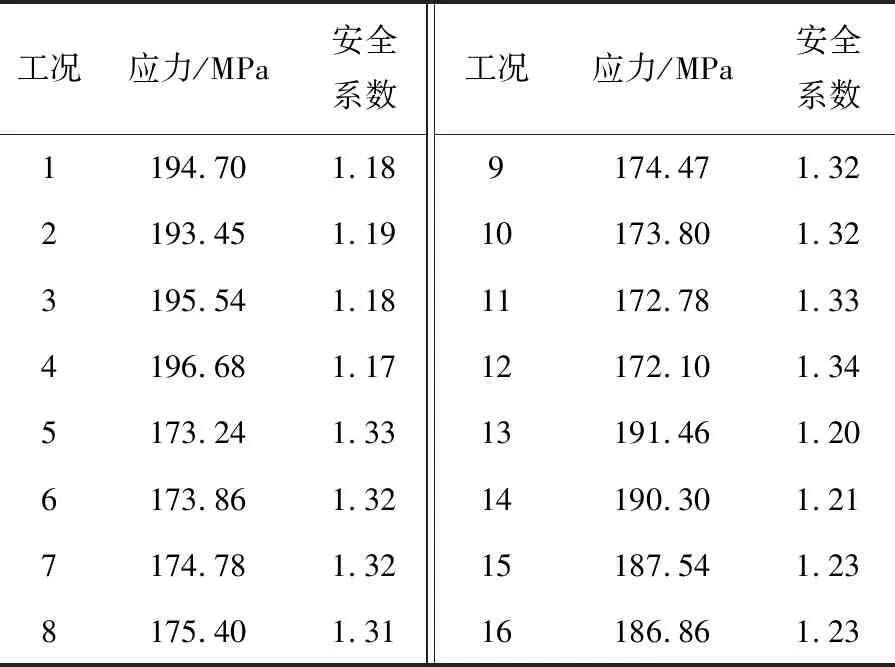
表5 不同工况齿轮箱体Von_Mises应力和安全系数

图3 载荷工况4齿轮箱上箱体的Von_Mises应力分布

图4 载荷工况4齿轮箱下箱体的Von_Mises应力分布

由表5中结果可知,齿轮箱体在不同载荷工况所产生的最大应力值不同,对应的位置也不同。在电机短路扭矩载荷不变的情况下,施加不同组合的载荷,对齿轮箱体的最大应力值有一定的影响。

4 齿轮箱体疲劳强度分析

4.1 疲劳强度评定方法

本文根据ERRI B12/RP17所提供的疲劳强度分析方法,对齿轮箱体结构进行疲劳强度计算。在有限元分析中,每个节点的平均应力和应力幅的计算式为:

σm=(σmax+σmin)/2

(1)

σa=(σmax-σmin)/2

(2)

式中:σmax为节点应力循环的最大等效主应力;σmin为节点应力循环的最小等效主应力。

用ERRI B12/RP17的投影法获得σm和σa的值,确定所有工况载荷下每个节点的应力幅值,用Haigh形式的Goodman疲劳曲线评定齿轮箱体的疲劳强度[12]。

QT400-18L的光滑试棒对称循环疲劳极限为σ-1s,由于实际结构的几何尺寸与形状、表面粗糙度和质量等级与光滑试棒存在差异,其结构的疲劳极限与试棒的疲劳极限满足:

(3)

式中:Kf为疲劳缺口系数;CL为载荷类型因子;ε为尺寸系数;β为表面状态系数;σ-1为光滑试棒的疲劳极限;σ-1k为缺口试棒的疲劳极限。

确定齿轮箱体材料的Goodman疲劳极限时,缺口试棒疲劳极限为122 MPa,CL=1.0,ε=0.9,β=0.8,则材料Haigh形式的Goodman疲劳曲线见图5。

图5 QT400-18L Haigh形式的Goodman曲线

4.2 计算结果与分析

在表4给出的载荷工况下,齿轮箱体节点应力幅与许用应力幅的比较见图6。表6给出了齿轮箱体应力幅最大的10个节点的相关参数。从图6和表6可以看出, 齿轮箱体应力幅值均小于其对应许用应力幅,最小安全系数为2.25,出现在259 940节点处。疲劳评估结果表明,齿轮箱体的疲劳强度满足许用要求,说明齿轮箱体在设计寿命周期内,可承受牵引和制动工况下的扭矩载荷及线路激扰产生的振动载荷,且不发生疲劳失效。

表6 应力幅最大的10个节点的相关参数

图6 齿轮箱体节点的应力幅与许用应力幅比较

5 结论

本文对轴悬式齿轮箱体的16种载荷工况进行了静强度和疲劳强度分析,分析结果如下:

(1) 在静强度载荷工况下,当短路扭矩为8 000 N·m时,对齿轮箱体的局部应力进行校核验证。齿轮箱体的最大应力(196.68 MPa)出现在齿轮箱上箱体齿面观察窗附近,其最小安全系数为1.17,静强度满足许用要求。

(2) 在复杂运行载荷工况下,应力幅值均小于其对应许用应力幅,齿轮箱体的疲劳强度满足许用要求。

(3) 疲劳强度评估结果表明,齿轮箱体在设计寿命周期内,可同时承受牵引/制动工况下的扭矩载荷及电机短路扭矩工况产生的振动载荷,且不发生疲劳失效。