重大节假日出行方式选择模型研究

何永明,张磊,魏堃,曹剑,王锦扬

(1.东北林业大学 交通学院,黑龙江 哈尔滨 150040;2.长安大学 道路结构与材料交通运输行业重点实验室,陕西 西安 710000)

2012年,国务院发布了《国务院关于批转交通运输部等部门重大节假日免收小型客车通行费实施方案的通知》,规定在重要节假日(春节、清明节、劳动节和国庆节)期间对小型车辆实行高速公路免费政策。该政策的出台推动了更多出行者在重要节假日期间选择高速公路出行。然而随着该政策的持续实施以及节假日交通量的不断增大,高速公路出现了严重的交通拥堵现象[1],由此引发的各类交通事故、资源浪费及环境恶化等问题也日益严重[2]。造成该现象的一个重要原因是缺乏对节假日期间出行特征的深入研究,没有具体地分析免费政策对出行选择的影响。

出行特征是交通领域的重要研究内容,主要包括出行距离、出行方式和出行频次等[3]。为合理引导交通需求空间分布,避免加剧节假日期间高速公路的交通拥堵,基于不同的出行特征建立联合选择模型,探讨节假日免费政策优化方向,是非常有必要的。在公路收费政策制定方面,学者们提出了分里程收费[4]、分时段收费[5]以及拥堵收费[6]等策略。从方法论而言,建立的模型包括多项Logit模型[7]、潜在类别模型[8]和贝叶斯网络模型[9]等。在多种出行联合选择模型中,巢氏Logit(Nested Logit,NL)模型克服了传统Logit模型的IIA特点,可充分考虑备选方案之间的相关性,被广泛用于出行预测分析。

基于以上分析,以NL模型为基础,结合2019年湖南省五一节假日期间出行调查问卷,构建出行方式与出行距离联合选择模型。通过该模型设计多种分里程免费政策,考察不同仿真场景下出行方式的变化,提高公共交通分担率,缓解节假日高速公路交通压力。

1 样本数据及特征

1.1 数据采集

以2019年湖南省五一节假日期间出行调查问卷数据为基础,研究出行者个人属性和收费政策对出行选择的影响。为详细分析不同因素对节假日出行选择的影响,调查问卷将影响因素分为个人属性及出行属性两类。个人属性包含性别、年龄、家庭人均年可支配收入及是否拥有汽车;出行属性包括节假日出行目的、节假日出行方式及出行距离[10]。共采集节假日出行调查问卷635份作为数据样本,问卷中出行者的基本统计信息见表1。

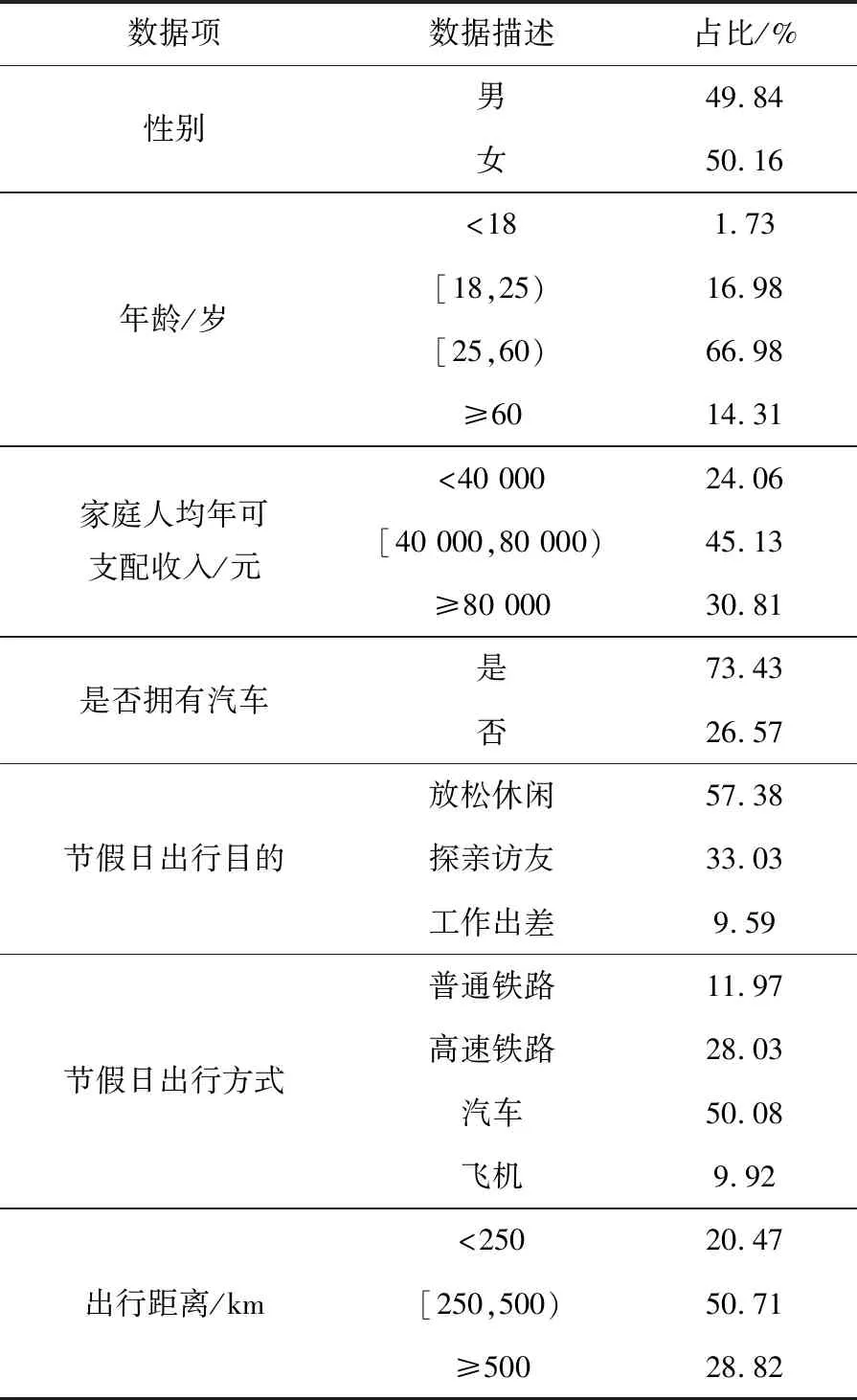
表1 样本基本统计信息

本次调查中拥有汽车的受访者高达73.43%,可见本样本成功捕捉到节假日期间受免费政策影响的主要出行群体。

1.2 数据特征

对表1中的样本数据特征进行分析,从出行方式分担率来看,汽车和铁路出行比例超过90%,为节假日出行的主要方式。出行距离的远近直接影响城际间相互作用的覆盖范围,是研究节假日城际交通特征的重要因素。五一节假日时间较短,出行邻近效应明显,出行距离可划分为三个等级[11]。由表1可知,选择中等距离([250,500) km)出行的人数较多,表明城际间相互作用明显。为研究五一节假日期间城际交通空间分布特征,对出行方式及出行距离进行联合统计,得到交通量空间分布,见图1。

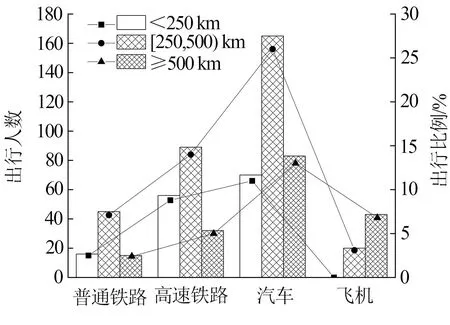
图1 交通量空间分布

图1反映了选择不同出行方式的出行距离比例分布。出行距离在250～500 km范围内的人数最多,符合五一节假日出行的邻近效应。选择汽车出行的人数最多,在500 km以内的距离上具有明显优势。选择飞机出行的人数最少,且多数出行者更希望完成一次长距离(≥500 km)的出行。铁路运输适用于不同等级的出行距离,但和选择汽车出行的人数相比数量较少。因此,有必要对节假日免费政策进行优化,促进不同等级出行距离下各出行方式分担率的均衡分布。

2 模型构建

NL模型又被称为嵌套Logit模型,该模型是在多项Logit模型的基础上扩展而来的,主要用来解决反应变量的各个类别之间存在的相关性问题。NL模型在一定程度上克服了多项Logit模型的IIA特性,即任意两类别的概率之比不会受到其他类别的影响[12]。因此,NL模型可用于出行预测等多个备选项间相互影响的离散选择行为。

构建出行方式与出行距离联合选择的NL模型,需要解决三个关键问题:①确定模型结构,即如何划分出行方式与出行距离的层次关系;②确立效用变量函数,即选择解释变量并确定函数形式;③推导选择概率,即确定备选方案的选择概率函数。

2.1 模型结构

NL模型中存在分层巢氏结构,具有相似特征的备选项被放入一个巢内。每个巢内的选择肢之间存在相关性,而不同巢的选择肢保持独立。由表1可知,节假日期间普通铁路、高速铁路和汽车承担了超过90%的出行量。既有研究表明,高速公路通行费用增加后, 出行方式会优先从汽车转为普通铁路和高速铁路[13]。因此,为避免备选方案数量过大,将对普通铁路、高速铁路和汽车3种主要出行方式进行建模。假设3种出行方式间具有独立性,同一出行方式的备选项具有相关性,可构建出行方式位于上层、出行距离位于下层的NL模型[14],结构见图2。

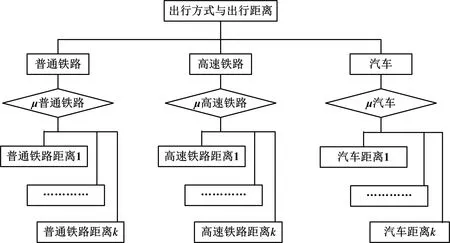
图2 NL模型结构

图2中,NL模型共包含3个巢,分别代表普通铁路、高速铁路和汽车这3种出行方式。每种出行方式对应的子集合包含k个选择肢,即k个出行距离。NL模型中选择肢集合为C={ci}(i=1,2,3,…,I),共包含I=3k个备选方案。μ(0<μ<1)为巢异质参数,μ值越接近0说明巢内选择肢之间相关性越大,反之表示相关性越小。

2.2 效用变量函数

随机效用理论认为备选方案的效用是随机函数,该函数由两部分组成,分别为确定效益和随机项:

Uni=Vni+ξni

(1)

式中:Uni为出行者n选择备选方案i时的效用;Vni和ξni分别为出行者n选择方案i时的确定效益和随机项。

根据随机效用最大化理论,若存在备选方案i(i∈C)的效用为Uni,则对任意不同于i的方案j,当且仅当Uni>Unj,出行者选择备选方案i。Vni是反映备选方案属性变量和出行者属性的函数。ξni用来描述出行属性调查过程中无法观测的因素对方案效用的影响。

(2)

确定效益Vni一般可以表示成多个解释变量Xnik的线性组合,其中Xnik表示出行者n在第i个备选方案中第k个变量,βik是Xnik的边际效应系数。ASCi是一个特定常数,用于捕捉系统中无法解释的可变性。通过考虑数据的可获得性并参考既有文献[15],可确定出行者变量、出行方式相关变量和行程特性变量三类解释变量(表2),并通过极大似然法估计解释变量的系数。

表2 解释变量及说明

2.3 选择概率

与多项Logit模型等广义极值分布模型一致,NL模型可获得具有固定形式的选择概率表达式。假设个体t的候选方案yt=1,2,3,…,m,在已知选择结果为集合At中的选择条件下,At中不同选择发生的概率服从标准多项式Logit模型,即对m∈At有:

(3)

式中:Wtm是具有k个选择肢的集合中相关变量的km个观测形成的行向量;βm是km维参数向量;θt可看作参数向量βm的尺度参数。经哑变量处理后,假定每个出行备选方案的效用误差均服从二项分布,则根据标准多项式Logit模型的选择概率表达式,推导出备选方案i的选择概率为[16]:

(4)

式中:P(k)为出行者选择出行方式k的概率;P(i|k)为出行者在出行方式为k的情况下选择备选方案i的概率,其值受各出行方式效用函数V和巢异质参数μ的影响;Ck为出行方式为k时的选择肢集合;j代表该集合内任一可选方案。

3 模型结果分析

3.1 模型结果

本文以单次出行为分析单元,基于表2描述的各解释变量构建NL模型。利用Python Biogeme平台对模型进行标定,模型生成映射文本及评估结果等文件。为避免出现严重多重共线性造成的模型失真,对经哑变量处理后的解释变量采取不完全输入方式,定义效用函数并输出估计参数值及t检验值,结果见表3。模型拟合优度ρ2反映解释变量对因变量变化的敏感度。实践中拟合优度ρ2的值达到0.4,即可认为模型精度较高[17]。参数估计结果中拟合优度ρ2为0.397,表明该模型可较好地模拟出行选择。

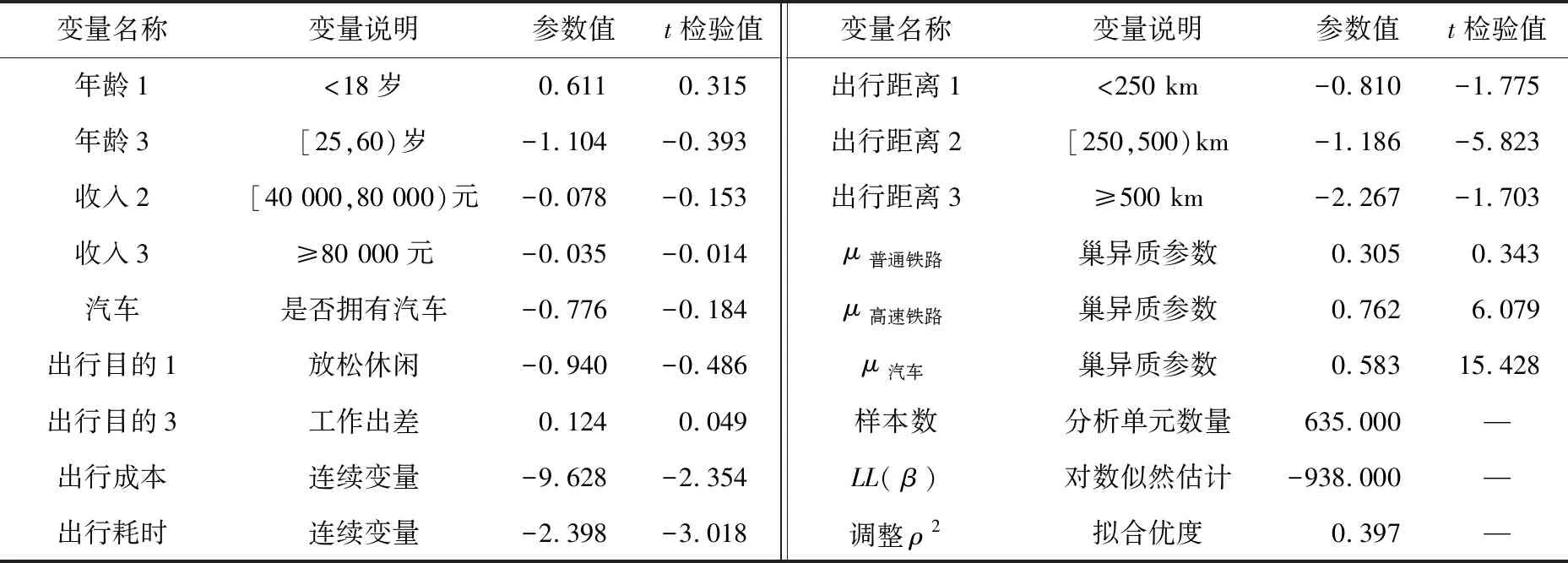
表3 模型参数估计结果

参数估计结果表明,出行成本和出行耗时参数值均为负,表明单一出行方式被选择的概率与出行成本和出行耗时呈负相关,即出行者更倾向选择出行成本低、出行耗时少的出行方式,符合研究预期。普通铁路、高速铁路和汽车的巢异质参数分别为0.305、0.762和0.583,均显著小于1。3种出行方式的巢异质参数表明同一种出行方式在不同出行距离下有较强的相关性。其中,高速铁路的巢异质参数最大,表明随着出行距离的增加,选择该出行方式出行的人数变化最大。

3.2 不同收费下分担率分析

弧弹性法可用于分析相同里程下不同收费标准和同一标准下不同收费里程对出行方式分布的影响。弧弹性指一个变量相对于另一个变量发生一定比例改变的属性,即出行者n选择备选方案i的概率P(i|n)对某一出行属性xin的敏感程度。弧弹性Ein揭示了属性变化过程中保持总收益最大的方法,其原理如式(5)所示:

(5)

分析节假日期间高速公路免费通行情况,选择小型车0.45 元/km为临界值,均匀设置9种对比场景。根据出行距离的不同,增加出行成本属性值,不同收费标准下汽车出行成本增幅不同。利用NL模型仿真出行者在不同汽车出行成本下各出行方式选择概率P(i|n)的变化。结合模型仿真结果计算出行方式分布对不同收费标准的弧弹性变化,分析结果见图3。其中纵坐标代表不同出行方式的弧弹性,横坐标中每个序号代表一种对比场景,例如序号1表示收费标准为0.05 元/km。

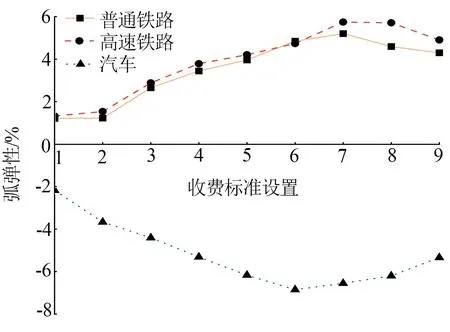
图3 收费标准弧弹性分析

此外,以所有里程收费标准都是0.45 元/km为参考对象,设置不同区间的出行里程收费为对比场景。参考表1中出行属性特征,以100 km为区间长度,共设置6种对比场景。通过NL模型仿真计算出行方式分布对不同收费里程的弧弹性变化,结果见图4。同理,图4中横坐标中每个序号代表一种对比场景。序号1表示收费里程为0～100 km,序号6表示收费里程为500 km以上(含500 km)。

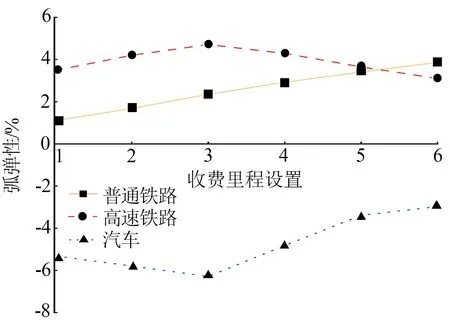
图4 收费里程弧弹性分析

由图3和图4可知,随着收费标准的提高,汽车出行成本升高,选择汽车出行的概率降低,弧弹性为负。原计划选择汽车出行的出行量转移至普通铁路和高速铁路,导致选择概率增加,弧弹性为正。收费标准对出行方式影响的显著性呈现先升后降的趋势,当收费标准为0.30～0.40 元/km时,影响最为显著。出行方式变化对收费里程的敏感度差异也较大。当高速公路在300 km以内进行收费时,不同出行方式间的交通量转移最为显著,此时出行者更倾向于选择高速铁路代替汽车出行。随着收费里程的增大,普通铁路乘客人数增加趋势明显,高速铁路乘客人数增加趋于平缓。综上所述,增加收费里程并提高收费标准,有利于提高公共交通的分担率,减少高速公路交通拥堵现象。

4 分里程收费仿真评价

4.1 场景设计

结合上述步骤对出行方式选择模型构建及弧弹性分析可知,节假日期间高速公路收费里程为300 km,且收费标准为0.30～0.40 元/km时出行方式改变更加显著。为进一步确定不同收费组合对出行方式选择的影响,通过场景仿真法构建多组收费里程和收费标准组合场景。收费里程分为3个等级(<150 km、[150,300) km、≥300 km);收费标准有3种形式(0.30 元/km、0.35 元/km、0.40 元/km)。选取不同距离的收费里程为横坐标,不同场景类别为纵坐标。以既有节假日免费政策为参考场景,对各等级距离下的出行,采取4种不同的收费标准设计64种节假日分里程收费场景,见图5。

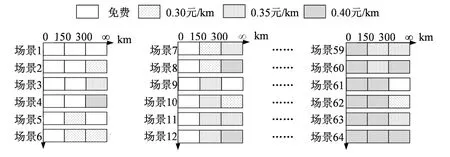
图5 分里程收费场景设计

4.2 仿真评价

将64种分里程收费场景导入已建成的NL模型,根据不同的收费标准组合调整汽车出行成本属性值,铁路出行成本属性值不变。读取汽车出行距离并计算不同场景下收取费用,则出行成本属性值为油费和收取费用之和。依次调整各场景出行成本属性值后进行仿真,导出不同出行方式选择人数和比例。以节假日免费政策下出行方式选择为参考系,统计相对于场景1的出行方式变化率,结果见图6。

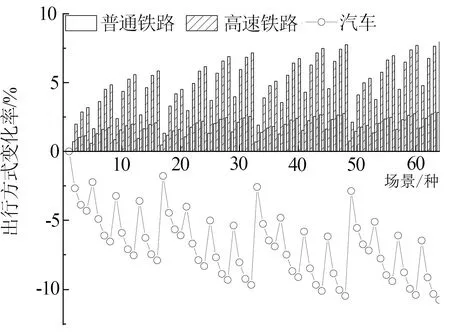
图6 出行方式变化率

由图6可和,与既有政策相比,短距离下对汽车出行进行收费会诱导出行者选择速度更快的高速铁路。随着出行距离的增加,出行者逐渐倾向于出行成本较小的普通铁路。相比于参考场景,提高收费标准使交通需求从汽车转为普通铁路和高速铁路,可以有效缓解节假日期间高速公路的交通拥堵。此外,出行方式对是否收费的敏感度较高,而对收费幅度变化的敏感度较低,且高速铁路对收费幅度变化的敏感度高于普通铁路。因此,为尽量减少出行成本,防止高速铁路压力过大,可对长距离出行收取小于0.45 元/km的费用。

5 结论

掌握出行方式和出行距离的联合选择特性是制定合理的节假日通行政策和方便出行的重要前提。通过构建以出行方式为上层,出行距离为下层的NL模型,结合五一节假日期间出行选择调研数据对出行方式分担率进行分析,并利用场景仿真法考察不同收费组合的影响,得到以下结论:

(1)NL模型参数估计结果表明,普通铁路、高速铁路和高速公路在不同出行距离下均具有较强的相关性,表明不同节假日出行政策下3种出行方式可替代性较高。此外,相较于出行者个人变量,出行方式相关变量(出行成本、出行耗时)对出行方式选择的影响较大。

(2)不同收费标准的分担率分析结果表明,提高收费标准和对不同出行距离进行分里程收费均能显著降低汽车出行的分担率,提高普通铁路和高速铁路的出行比例。随着收费标准和收费里程的变化,各出行方式的弧弹性会出现较大差异。

(3)不同收费组合的场景仿真结果表明,对长距离出行收费更容易诱导出行者选择普通铁路,从而缓解节假日高速公路拥堵,同时避免高速铁路购票难的情况。

本文出行选择模型基于邻近效应明显的五一节假日出行需求,未考虑节假日城际交通特征的变化,具有一定的局限性。后续研究将考虑出行时间和季节等因素对城际出行的影响,进一步完善节假日免费政策。