无杆式高压气动弹射器弹射性能参数灵敏度分析

王雪琴,朱阿元,马吴宁,刘 栋,王尚龙

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.航空工业成都飞机工业(集团)有限责任公司,四川 成都 610031;3.陆军研究院工程设计研究所,江苏 南京 210016)

随着导弹武器系统的发展,压缩空气冷弹射技术越来越成熟,在其他领域的应用也越来越广泛。与传统火药燃气冷弹射方式相比,压缩空气冷弹射方式以常温压缩空气作为动力源[1],将导弹武器弹离弹射装置一定距离后,再启动发动机进行工作[2],可降低发射阵地红外特征,对热防护要求低,内弹道可控性好,进而提高生存能力[3]。

目前,国外已有部分国家将压缩空气弹射运用在军事或商业上[4],还有部分国家的学者在进行相关理论研究及运用探索[5]。国内学者针对压缩空气冷弹射方式的研究主要集中在筒式发射与非筒式发射2大类上,其中筒式发射根据被弹射物的不同分为筒式导弹弹射[2,6]、筒式无人机弹射[7,8]、筒式角反射器弹射[9]等;非筒式发射根据弹射装置结构及被弹射物的不同分为提拉式导弹弹射[3]、提拉式鱼雷弹射[10]、轨道式导弹弹射[11,12]、轨道式无人机弹射[13]等。

李博平等[2]针对筒式压缩空气导弹弹射系统,导出内弹道数学模型,进行数值仿真并分析了3种系统参数对内弹道特性的影响规律;刘南宏等[8]针对筒式压缩空气无人机弹射系统,通过动力学分析软件建模仿真,再与弹射试验结果对照,针对弹射过程中筒内气体流动特性做出了详细分析;帅超等[9]针对压缩空气充气式角反射器抛射系统,理论推导了气瓶及角反射器运动的联合数学模型,得出的气瓶压力仿真结果与试验数据对比基本吻合,并对抛射过程内弹道的影响因素进行了详细分析;徐勤超等[10]针对压缩空气提拉式鱼雷弹射装置,采用联合仿真的方式建立动力学模型并求解,将仿真结果与试验数据进行对比验证,证明该发射方式可行;姚琳等[3]针对压缩空气两级提拉式单侧导弹冷弹射装置采用彭-罗宾逊(Peng-Robinson,P-R)真实气体方程,建立了弹射内弹道模型并实现联合仿真,详细分析了弹射过程中各提拉缸内压力、温度变化过程并给出导弹的运动学参数,最后以气源容积最小为目标函数应用遗传算法进行优化设计;王雪琴等[11]针对双缸对称轨道式导弹弹射系统,基于标准干空气真实气体热力学状态方程,建立精确内弹道模型并详细分析考虑泄露的弹射过程中热力学参数与负载运动参数的变化规律,并与试验数据、流体仿真结果对比;Zhang等[13]以轨道式无人机弹射系统为研究对象,在协同仿真的基础上建立了气动发射装置动态仿真模型并通过试验进行验证,给出了关键参数对发射过程动力学特性性能的影响,并对装置结构进行了优化。

纵观上述文献可知,弹射装置的弹射性能受到各种参数的直接影响,已有文献在研究内弹道性能影响因素时,未考虑多参数同时变化的影响。压缩空气弹射过程时间短,弹射性能在多参数共同作用下变化复杂,因此不仅参数本身变化,多参数同时变化的耦合作用也会对弹射性能产生一定的影响,需要对此进行进一步的分析。

本文针对固有结构存在一定泄漏的双缸对称无杆式高压气动弹射器,基于高压空气的真实热力性质参数,理论推导了弹射过程的数学模型,利用全局灵敏度分析方法,对内弹道稳定性及离轨速度的主要7个参数进行了影响规律分析,确定了内弹道稳定性及离轨速度的主要影响参数,并分析了参数的线性主效应、二阶效应。

1 高压气动弹射器结构及发射原理

双缸对称无杆式高压气动弹射器模型的结构见图1。

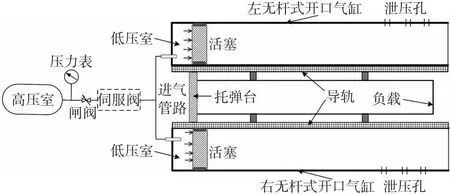
图1 双缸对称无杆式高压气动弹射器结构图

该弹射器主要由高压室、进气管路、低压室、活塞、托弹台等部件构成。其中进气管路为低压室初始容积,负载开始运动后,进气管路和低压室共同组成低压室。其工作原理为:控制箱发出弹射指令,阀控随即响应,控制阀门打开;高压气体进入初容室(进气管路),经进气管路分流后分别流入左右气缸,当气体累积推力大于负载自重及阻力时,推动活塞带动托弹台及负载一起运动,两侧活塞组件被相对应的缓冲油缸组件缓冲制动,此时负载与托弹台分离,一次完整发射完成。

2 发射过程数学模型

假设:(1)弹射过程时间短,忽略传热;(2)忽略气体动能和势能;(3)忽略气体粘性;(4)两侧气缸压力平衡;(5)活塞达到推弹行程时气体及时泄出,忽略剩余气体对缓冲的影响。

2.1 干空气的状态方程

标准干空气的状态方程采用无量纲亥姆霍兹能的形式来表达,是使用最小二乘法基于现有试验下的压力p、密度ρ、温度T、热容、声速和气液平衡数据拟合而来,该方程表示为

(1)

式中:a(ρ,T)表示亥姆霍兹能,α0(δ,τ)为理想气体对亥姆霍兹能量的贡献部分(简写为α0),上标0表示理想气体性质,αr(δ,τ)为对亥姆霍兹能量的剩余贡献部分(简写为αr),上标r表示剩余性质;δ=ρ/ρj表示约化密度,ρj表示最大冷凝密度,τ=Tj/T表示约化温度的倒数,Tj表示最大冷凝温度,α0(δ,τ)、αr(δ,τ)的表达式分别如式(2)、式(3)所示

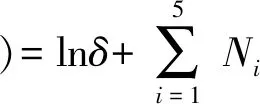
N7lnτ+N8ln[1-exp(-N11τ)]+

N9ln[1-exp(-N11τ)]+N10ln[2/3+

exp(N13τ)]

(2)

(3)

α0(δ,τ)中系数Ni及αr(δ,τ)中系数ik、jk、lk的具体数值详见文献[14]。

用于计算压力p、比热力学能u、比焓h的公式如下

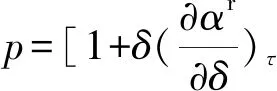
(4)

(5)

(6)

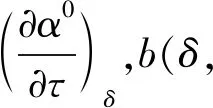
u=RT[a(τ)+b(δ,τ)]

(7)

h=RT[a(τ)+b(δ,τ)]+RTc(δ,τ)

(8)

上文中所用的标准干空气参考常数如表1所示。

表1 干空气的参考常数

2.2 伺服阀控制方程

弹射过程中喷口流量方程为[13]

(9)

式中:μx为流量修正系数;A为阀开口截面积;k为绝热系数;R为空气气体常数;下标“H”表示与高压室相关的参数,下标“L”表示与低压室相关的参数;p为气体压力,T为气体温度。

考虑到与弹射试验的对比,给出试验所用阀的简图,如图2所示。

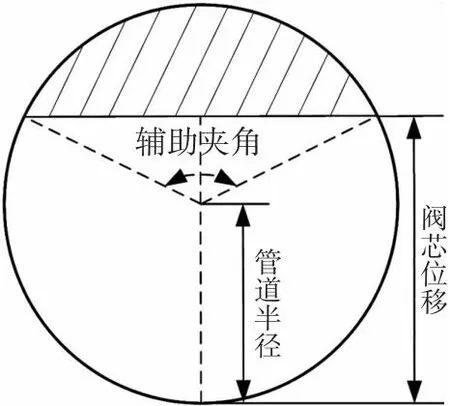
图2 气阀简图

根据平面几何原理,得出A、辅助夹角θ与阀芯位移d、阀门管道半径(下文简称阀径)r的关系式如式(10)、(11)所示

(10)

(11)

2.3 高、低压室控制方程

分别根据质量、能量守恒方程以及活塞的运动微分方程,建立数学模型

(12)

式中:下标“H”表示与高压室相关的参数,下标“L”表示与低压室相关的参数;ρ为气体密度,V为容积,u和h分别为比热力学能和比焓,mL为流入低压室的气体质量,n为开口气缸数目,η为根据试验数据拟合的泄漏率公式[11],l为弹射行程,S为活塞推力面积,v为弹射速度,pa为标准大气压力,me为弹射质量,g为重力加速度,α为发射角。

(13)

3 内弹道参数分析

3.1 理论仿真结果与试验数据及流体仿真结果对比

根据上文推导的精确内弹道数学模型,采用四阶龙格-库塔(Runge-Kutta)法,在MATLAB 2014a环境下求解。初始值及各种参数取值如下:ρH=153 kg/m3,TH=300 K,mL=0.235 4 kg,ρL=1.177 kg/m3,TL=300 K,VH=2.5 m3,V0=0.1 m3,S=0.1 m3,n=2,α=88,k=1.4,μx=0.96,r=125 mm,pa=10 132.5 Pa,me=16 000 kg,t=0.8 s。

参考文献[11]的5.2和5.3小节分别详细给出了理论仿真结果与试验数据的对比及理论仿真结果与流体仿真结果的对比,考虑到实际试验过程中的复杂因素无法一一复现,认为2种仿真计算结果均与试验结果总体基本一致,验证了弹射原理及弹射过程内弹道模型的正确性。

3.2 试验设计方法

随着试验设计方法的不断研究以及计算机技术的快速发展,拉丁方系列设计因为具有更好的空间填充性能所以被广泛应用,其中最优拉丁超立方设计具有较好的空间填充性和均衡性能,能使所有的试验点尽可能均匀地分布在设计空间之内[15],因此本文使用该设计方法进行设计变量采样。

3.3 试验设计过程

在相同条件下,导弹达到推弹行程le时离轨速度(以下简称ve)越大,标志着弹射品质越高。内弹道弹射过程是否稳定采用内弹道稳定性参数ks来进行评价,ks的具体计算式为[16]

(14)

式中:amax为弹射过程的最大加速度值,acp为达到该出筒速度所需的等加速度平均加速度,根据工程经验ks≥1,其值越大表示导弹发射越不稳定。

基于第2节所建立的精确内弹道数学模型,总结出对ve、ks有影响的因素共7个:高压室气体密度ρH、环境温度T1、泄露率倍数XL、高压室容积VH、低压室初始容积V0、阀径r、气动阀的开启时长To,经过试算,给出各影响因素的最佳取值范围,如表2所示。

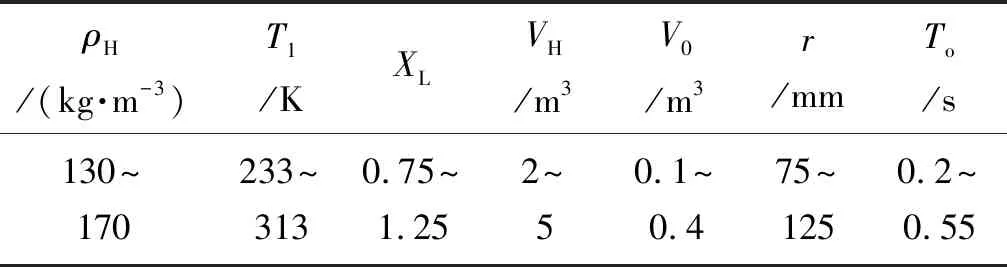
表2 影响因素的取值范围

综合考虑7个变量的影响,最终采用350组样本空间来进行灵敏度分析。

3.4 全局灵敏度分析方法

多元二次回归模型为

(15)

以2个输入变量y1、y2模型为例,其多项式构成如下

(16)

则其导数为

dz=b1dy1+b2dy2+2b3y1dy1+2b4y2dy2+b5d(y1y2)

(17)

y1、y2线性项的主效应为b1y1、b2y2,二阶项主效应为2b3y1dy1、2b4y2dy2,二阶项交互效应为b5d(y1y2),式(15)和式(16)的各种系数详见文献[15]。由式(17)可知,分析影响因素的敏感度不仅要分析影响因素的线性效应,还需分析影响因素的二阶效应,且各影响因素可能交互作用。

ve、ks的影响因素敏感度分析流程如图3所示。

图3 影响因素敏感度分析流程图

3.5 全局灵敏度结果

(1)影响因素线性主效应分析

图4和图5分别给出了7个影响因素对ks、ve的线性主效应分析图。

图4 影响因素对ks的线性主效应分析

图5 影响因素对ve的线性主效应分析

由图4可以看出:在影响因素的取值范围内,内弹道指标ks对影响因素的敏感性高低顺序依次为:VH、T1、r、V0、To、ρH、XL,其中前6项为负效应,第7项为正效应,VH对内弹道指标ks的影响存在明显的非线性关系。

对于VH,随着VH增大,ks值减小,且ks值减小的变化率越来越小,表明VH越大,导弹发射越稳定。从式(12)可知,高压室初始压力值一定时,VH越大,弹射时高压室内气体密度变化率越小,高压室剩余气体压力越大,气体量越充足,联系式(9)可知,流入低压室的气体质量流量越大,低压室初始建压压力也越大,弹射中后期过载曲线能较好地维持使得平均加速度更稳定,反映到内弹道上即ks值越小。从实际发射过程分析,每次弹射过程的耗气量是一定的,当VH足够大时,气体量十分充足,弹射中后期过载曲线能较好地维持,反映到内弹道上即ks值越小。

对于T1,随着T1增大,ks值减小,表明T1越高,导弹发射越稳定,从式(4)可知,环境温度直接影响压力大小,对于高压室而言,初始温度越高,高压室内初始压力越大,联系式(9)可知,随温度升高,流入低压室的气体质量流量越大,低压室内初始建压压力也越大,在低压室压力建立完成后,即开始推动活塞带动托弹台及弹体一起运动。流入低压室的气体质量流量越大,也使得弹射中后期过载曲线能较好地维持使得平均加速度更稳定,反映到内弹道上即ks值越小。

对于r,随着r增大,ks值减小,且ks值减小的变化率越来越小,表明r越大,导弹发射越稳定。从式(10)可知,在阀芯最大位移值为定值的情况下,r越小,A越小,联系式(9)可知,流入低压室气体的质量流量越小,阀门节流情况越严重,使得弹射中后期过载曲线不能维持,反之,在高压室内气量足够的情况下,r越大,A越大,流入低压室气体的质量流量越大,低压室气体初始建压压力也越大,弹射中后期过载曲线能较好地维持使得平均加速度更稳定,反映到内弹道上即ks值越小。由于整个气体流动管路的等效通流面积是一定的,当r增大到一定值后会失去节流效果,r继续增大但ks值趋于稳定。

对于V0,随着V0增大,ks值减小,表明V0越大,导弹发射越稳定。从式(13)可知,V0越大,低压室内气体密度的变化率越小,低压室气体初始建压压力值越小,同时之后衰减得越慢,使得过载曲线整体更平稳,反映到内弹道上即ks值越小。

对于To,随着To增大,ks值减小,表明To越大,导弹发射越稳定。从图2可知,随着阀门的开启,A逐渐变大,高压室气体通过阀门不断向低压室流动,导致高压室压力持续降低,低压室压力快速升高。To直接影响低压室压力建压过程的快慢,To越长,建压过程越平稳,低压室气体初始建压压力值越小,同时后续流入低压室的气体质量流量越平稳,低压室压力衰减得越慢,使得过载曲线整体更平稳,反映到内弹道上即ks值越小。

对于ρH,随着ρH增大,ks值减小,且ks值减小的变化率越来越小,表明ρH越大,导弹发射越稳定。从式(4)可知,ρH直接影响压力大小,其值越大高压室压力值越大,气体量越充足,联系式(9)可知,流入低压室气体的质量流量越大,低压室气体初始建压压力也越大,弹射中后期过载曲线能较好地维持使得平均加速度更稳定,反映到内弹道上即ks值越小。当ρH足够大时,气体量十分充足,弹射中后期过载曲线能较好地维持,反映到内弹道上即ks值越小。

对于XL,随着XL增大,ks值增大,表明XL越大,导弹发射越不稳定。从式(13)可知,泄露率越大,流入低压室气体质量的变化率越小,低压室初始建压压力也越小,根据文献[11]可知,低压室建压完成后泄露率公式中9.710×10-4l一项起主要作用,使得泄漏率增大。XL越大,整体泄露率数值越大,使得低压室的压力下降更快,弹射中后期过载曲线不能较好地维持,反映到内弹道上即ks值越大。

由图5可以看出:在影响因素的取值范围内,内弹道指标ve对影响因素的敏感性高低顺序依次为:T1、ρH、VH、V0、r、XL、To,其中第1、2、3、5项为正效应,第4、6、7项为负效应。

对于T1、ρH、VH及r,均表现为数值越大,离轨速度ve越大。从上文对于T1、ρH、VH及r对ks值影响规律的分析中可知,T1、ρH、VH及r越高,整体过载值越大,反映在内弹道上,即ve越大。

对于V0、XL及To均表现为数值越大,离轨速度ve越小。从上文对于V0、XL及To对ks值影响规律的分析中可知,V0、XL及To越高,整体过载值越小,反映在内弹道上,即ve越小。

(2)影响因素二阶效应分析

图6分别给出了对ks、ve而言,影响因素二阶效应分析结果的前10组敏感度较大的影响百分比。由图6(a)可看出对ks而言,影响因素二阶效应的敏感性高低顺序依次为:VH^2、VH-T1、r^2、VH-V0、VH-ρH、T1^2、r-VH、V0-ρH、ρH-T1、r-V0,其中第7、8项为负效应,其余8项为正效应;对ve而言,影响因素二阶效应的敏感性高低顺序依次为:VH^2、ρH-T1、T1^2、VH-V0、ρH^2、VH-T1、VH-ρH、r^2、r-VH、V0-T1,其中第1、3、5、8、10项为负效应,其余5项为正效应。

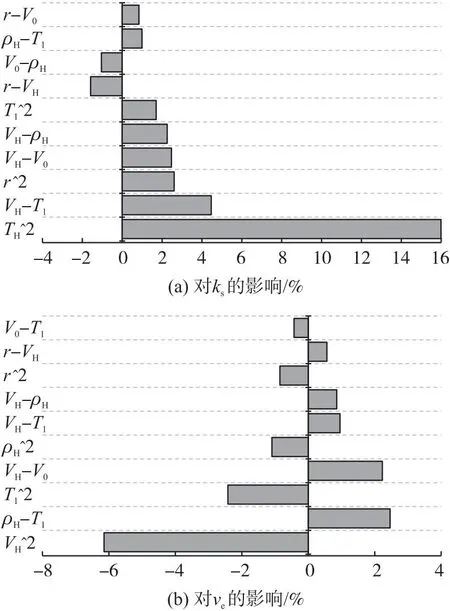
图6 前10组敏感度较大的二阶影响因素

图7和图8按敏感性高低顺序分别给出了对ks、ve而言影响因素二阶交互效应图。从图7和图8可知:对ks、ve而言存在二阶交互效应的影响因素均为以下5个:VH、T1、r、V0、ρH。

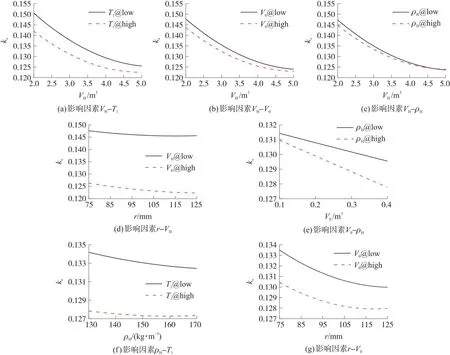
图7 影响因素对ks的二阶交互效应

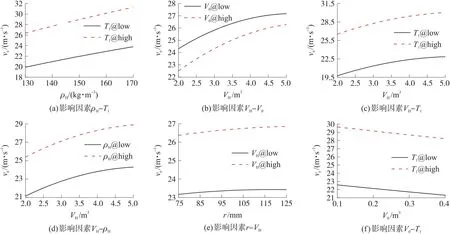
图8 影响因素对ve的二阶交互效应

由图7可知,以下6组:VH-T1、VH-V0、r-VH、V0-ρH、ρH-T1、r-V0的2个因子对ks值交互效应的2条线不是完全平行,对ks值有一定的交互效应,VH-ρH这2个因子对ks值交互作用中2条线交叉,表明存在强烈的交互作用;由图8可知,以下6组:ρH-T1、VH-V0、VH-T1、VH-ρH、r-VH、V0-T1的2个因子对ve交互效应的2条线不是完全平行,对ve值有一定的交互效应。

综上,7个影响因素中,均为VH、T1、r、V0、ρH这5个影响因素两两之间对ks、ve有一定的交互效应,剩余2个影响因素:XL及To自身的二阶主效应及与其余5个影响因素的二阶交互效应敏感度比较低,因此设计中可依据试验设计分析结果提前决定这2项的取值,实现设计变量的缩减。

从上文3.5节影响因素线性主效应分析结果中可知:XL越大,ks值越大,发射稳定性越差,同时ve值越小;反之XL越小,ve值越大,发射品质越高。考虑到减小泄露率倍数意味着装置重量的增加,此外,XL对ks、ve值的影响敏感性比较低,因此XL仍取原值1;To越长,ks值越小,发射稳定性越好,但使得ve值越小,发射品质越低,考虑到To对ve值的影响敏感性很低,因此最终对To取值0.55 s。

4 结论

(1)内弹道指标ve对影响因素的敏感性高低顺序依次为:T1、ρH、VH、V0、r、XL、To,其中第1、2、3、5项为正效应,第4、6、7项为负效应。

(2)内弹道指标ks对影响因素的敏感性高低顺序依次为:VH、T1、r、V0、To、ρH、XL,其中前6项为负效应,第7项为正效应,VH对内弹道指标ks的影响存在明显的非线性关系。

(3)影响ks最灵敏参数为VH,VH越大,导弹发射越稳定;影响ve的最灵敏参数为T1,T1越高,压力值越大,整体过载值越高,ve也越大。

(4)高压室容积自身的二阶主效应对ks及ve影响均最大;XL及To自身的二阶主效应及与其余5个影响因素的二阶交互效应敏感度较低,设计中可提前决定这2项因素的取值,实现设计变量缩减。

(5)下一步可根据本文的研究内容进行内弹道及弹射装置参数优化。