基于改进奇异谱分析的毫米波生物雷达干扰抑制方法

刘震宇，李成光，王梓斌

（广东工业大学 信息工程学院, 广东 广州 510006）

新冠肺炎的爆发严重危害人类的健康，其变体奥密克戎具有更高的传染性[1]。非接触生命体征检测可以减少医生与患者之间的交叉感染风险。它还可以应用于烧伤病人的监测、婴儿的呼吸暂停监测和老人的行为监测[2]。

作为新一代电子信息技术，基于调频连续波(Frequency Modulated Continuous Wave, FMCW) 的毫米波生物雷达在非接触生命体征检测领域受到了广泛关注。但是，随着雷达在越来越多的场景中应用，雷达之间的互扰将会成为一个严重的问题。干扰在时域表现为一个类脉冲信号，在频域拓展到整个频谱[3]。因此，雷达间的互扰使差拍信号的相位受到损坏，造成生命体征信号被淹没。

抑制雷达间互扰的方法分为主动干扰抑制和被动干扰抑制[4]。主动干扰抑制需要波形设计，随机跳频和伪噪声编码[5]调制是主动的干扰抑制方法。但是，主动干扰抑制方法会增加雷达系统的复杂度。被动干扰抑制方法通过信号处理实现，分为干扰信号重构与干扰信号分离的方法。关于干扰信号重构的方法，文献[6]提出将时域信号的受干扰部分置零的方法，但这样会造成相位的不连续；文献[7]提出了一种利用自回归模型恢复受干扰信号的方法，以消除由于干扰置零带来的相位不连续，但这种方法不能准确地找到干扰信号的起点和终点的位置。为了干扰信号更好地分离，形态分量分析的方法被提出来[8]。然而，这种方法不能检测到差拍信号受到干扰。为了解决这个问题，一种改进的形态分量分析方法被提出来[9]，但该方法很难找到最优的稀疏系数。

作为一种数据自适应和非参数方法，奇异谱分析(Singular Spectrum Analysis, SSA) 被用于信号分析[10]。它可以把原始时间序列分解成加性分量，例如振荡和噪声。为了消除噪声，传统的方法根据奇异值的能量对不同的分量进行分组，具有高能量的奇异值对应的分量是所需要的分量。

然而，在存在雷达互扰的情况下，受干扰差拍信号不仅包含目标和噪声分量，还包含干扰分量。干扰分量对应的奇异值的能量非常大，会混淆目标分量对应的奇异值。

综上所述，针对毫米波雷达间的互扰造成生物雷达获取的微弱生命体征信号被淹没的问题，本文考虑了基于改进奇异谱分析的毫米波生物雷达干扰抑制方法，主要贡献和创新点如下：

(1) 提出一种基于互相关的SSA方法抑制生物雷达干扰，修复受干扰的差拍信号，把目标分量从干扰和噪声中分离。

(2) 进一步提出基于信息熵的集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)方法抑制残留的相位噪声。

(3) 实测实验结果表明，本文所提方法能够有效抑制生物雷达的干扰，恢复生命体征信号。

1 生物雷达与干扰

1.1 生命体征检测原理

基于毫米波生物雷达的生命体征检测系统如图1所示。生物雷达射频前端产生线性调频连续波信号，即chirp信号。然后从发射天线发射chirp信号，照射到人体目标的胸腔。当人在交替吸气和呼气的时候，胸腔会产生类似于正弦运动的位移。此外，心跳也会引起胸腔的轻微运动。信号从目标的胸腔反射到达接收天线。反射信号的相位被胸腔运动调制[11]。

图1 基于毫米波生物雷达的生命体征检测系统Fig.1 Vital sign detection system based on millimeter wave bioradar

毫米波生物雷达获得的差拍信号可以表示为

式中：σ 为差拍信号的幅度；fb为差拍信号的频率；j为复数虚部号；φb=4πfc(R0+VS(ts))/c为差拍信号的相位，fc为 chirp信号的起始频率，R0为生物雷达与人体之间的初始距离，V S(ts)为人体胸腔的位移。

为了定位人体目标，对差拍信号YB(t)执行快速傅里叶变换(Fast Fourier Transform，FFT) ， 即距离维FFT。幅度谱的峰值对应于差拍信号的频率fb，可以得 到人 体目 标的 距 离Rtarget=cfb/(2θ) ，其 中θ 为chirp信号的斜率。

为了获得胸腔运动的信息，在每个差拍信号的距离维FFT中提取目标所在位置的相位。然后计算相位差 Δφb=4πΔVS(ts)/λ ，其中λ =c/fc为波长。最后，相位差被用于提取生命体征信息。

1.2 生物雷达干扰模型

雷达间的互扰如图2所示。图中的fc、Tc和WB分别为生物雷达的chirp信号的起始频率、持续时间和带宽。fI、TI和WI分别为干扰雷达的chirp信号的起始频率、持续时间和带宽。tI为干扰雷达发射chirp信号与生物雷达发射chirp信号的时间差。fLPF为生物雷达的低通滤波器带宽。

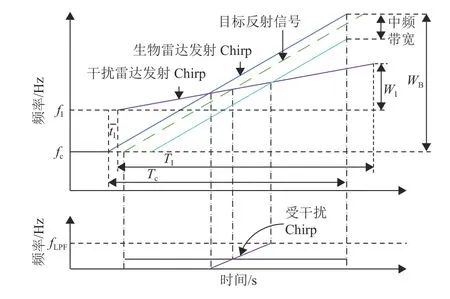
图2 雷达间的互扰Fig.2 Mutual interference between radars

干扰信号的产生与雷达发射信号的斜率有关，如图2的上半部分所示。当两个雷达的chirp信号相遇，如果混频后的频率差在低通滤波器的范围内，会产生干扰，如图2的下半部分所示。

受干扰的差拍信号可以表示为

式中：AT、θ 和φ0分别为生物雷达的chirp信号的幅度、斜率和初始相位。AI、θI和φ1分别为干扰雷达的chirp信号的幅度、斜率和初始相位。

因为干扰雷达信号直接到达生物雷达，而目标信号通过反射到达生物雷达。因此，当目标和生物雷达之间的距离与干扰雷达和生物雷达之间的距离相同时，干扰的信号能量远大于目标的信号能量，这在时域中表现为类脉冲干扰，如图3(a)所示。

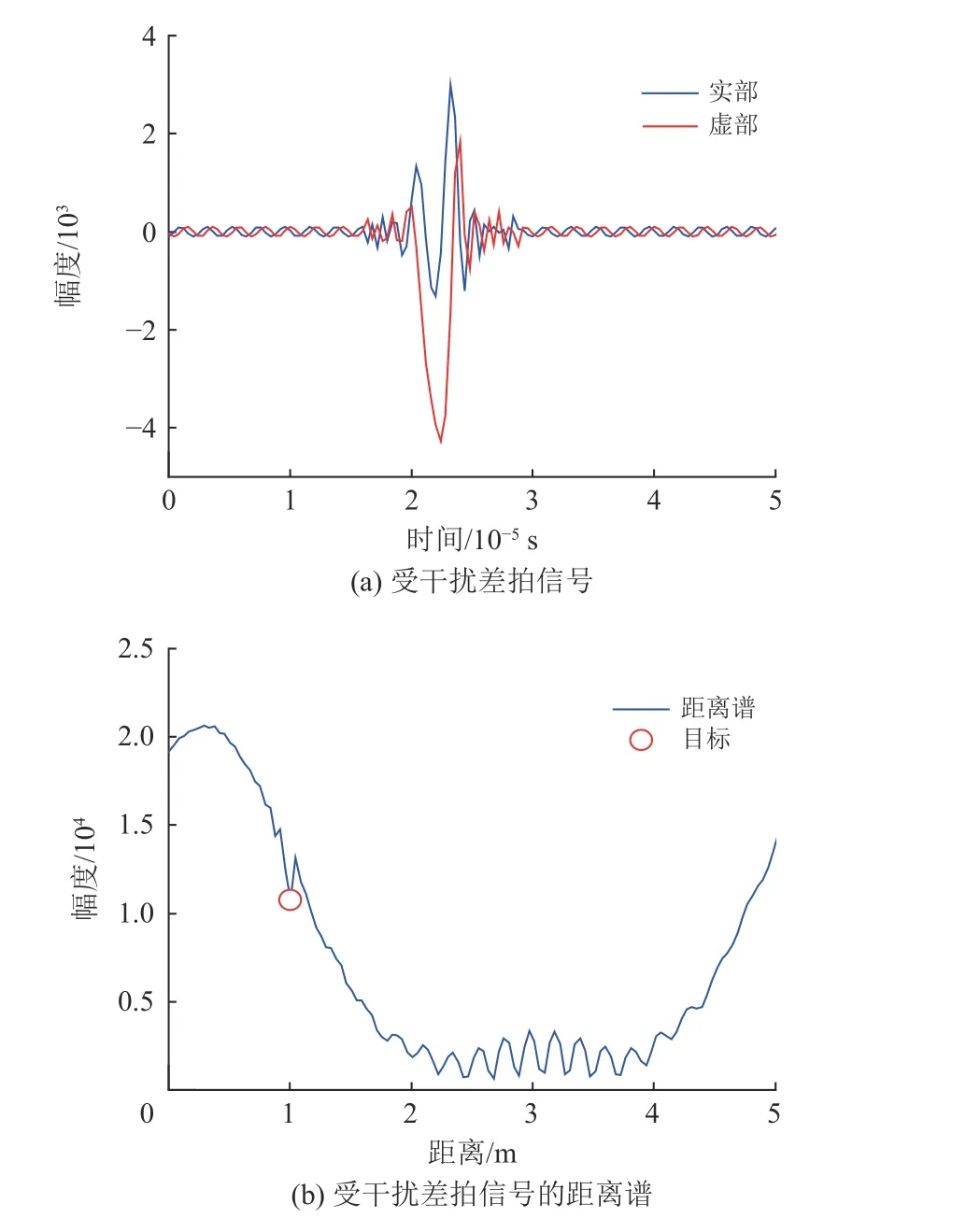
图3 雷达干扰对差拍信号的影响Fig.3 The influence of radar interference on the beat signal

如图3(b)所示，雷达之间的互扰会增加差拍信号的噪底，使目标被淹没或被错误检测，导致目标的生命体征信号被淹没。这降低了生命体征检测的准确性，因此需要对干扰进行抑制。

2 干扰抑制方法

奇异谱分析是研究非线性时间序列数据的重要方法[12]。使用奇异谱分析，可以将受干扰差拍信号分解为目标、干扰和噪声分量。如图4(a)所示，对于无干扰的差拍信号，目标的奇异值的能量占主导地位。然而，在互扰的情况下，干扰分量对应的奇异值的能量很大，这混淆了目标分量对应的奇异值，如图4(b)所示。利用奇异值的能量很难将目标分量和干扰分量区分开来。

图4 雷达互扰混淆奇异值能量Fig.4 Radar mutual interference confuses singular value energy

因为互相关具有描述或判断两个不同信号之间相关性的数学特性[13]。因此，本文提出基于互相关的SSA方法抑制干扰，采用互相关选择目标对应的奇异谱分量。因为抑制干扰后有残留相位噪声，因此还提出基于信息熵的EEMD方法进一步抑制残留相位噪声。所提出方法的信号处理流程如图5所示。

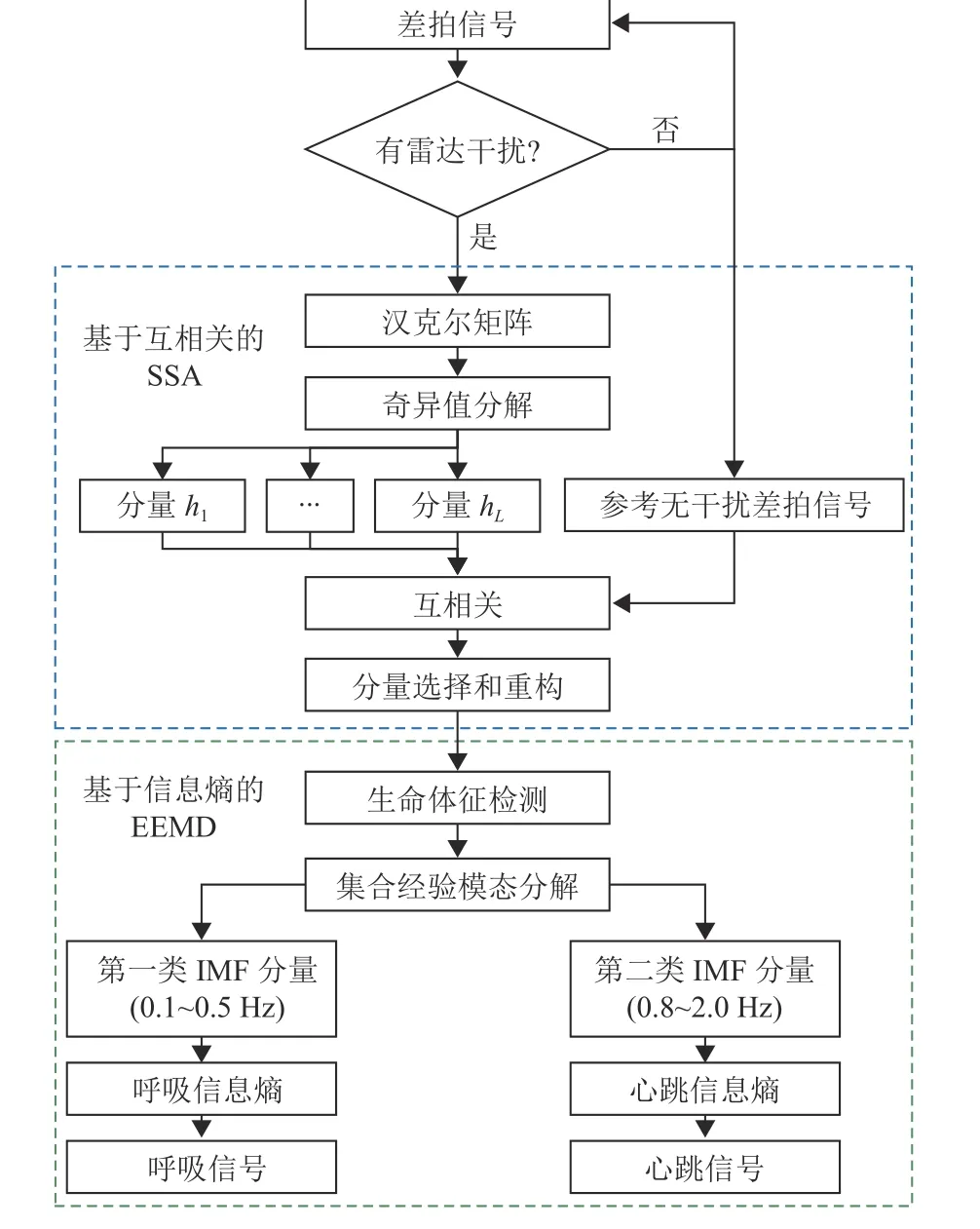
图5 所提出方法的流程图Fig.5 Flow chart of the proposed method

2.1 基于互相关的SSA干扰抑制方法

2.1.1 受干扰差拍信号检测

没有雷达干扰时，混频器的信号输出为式(1) 中的YB(t)， 其离散序列为Y1B:Q,1:Nc，其中Q为chirp信号的总数，Nc为单个chirp信号的采样点数。

雷达的干扰为类脉冲干扰，如图3(a)所示。根据差拍信号的标准差YSD与 均值Ymean的比值来判断差拍信号是否受到干扰。若(YSD/Ymean)≥th，则chirp受到干扰。t h为阈值，可根据实验设置。

2.1.2 受干扰差拍信号分解

式中：U为左奇异向量，V为右奇异向量，Σ 为由奇异值组成的对角矩阵，上标T为转置。在矩阵H中，受干扰信号被分离为目标、干扰和噪声分量。每个分量Hi通过对角平均转化成一维信号hi。

2.1.3 目标分量选择与重构

计算互相关需要无干扰差拍信号作为参考信号。由于雷达在生命体征检测中会发出Q个chirp信号，因此可以得到一些无干扰的差拍信号。

通过计算参考无干扰差拍信号与受干扰差拍信号分解的分量之间的互相关值，再根据互相关值来获取目标分量。互相关表示为

式中：符号* 为复共轭，hi(i=1,···,L)为受干扰差拍信号分解的分量，YB为 参考无干扰差拍信号，m为求互相关时的移位，m=[-(Nc-1),···,Nc-1]。

在得到每个分量的互相关值之后，选择互相关值最大的分量，从而得到目标分量。然后，对目标分量进行重构以恢复差拍信号。

2.2 基于信息熵的EEMD抑制残留噪声

干扰被抑制后，存在干扰残留相位噪声。由于生命体征信号是非线性非平稳信号，考虑到EEMD是一种自适应时频数据分析方法，适合对非线性非平稳信号进行分析，因此利用EEMD抑制相位差的残留噪声，提取呼吸和心跳信号。

EEMD是EMD方法的改进，是为了消除模态混叠问题而提出来[14]。经过EEMD分解后得到

式中： ωj为第j个固有模态函数(Intrinsic Mode Function, IMF) 分量，J为IMF分量的总数，rJ为残差。

EEMD对相位差进行分解后，需要区分生命体征信号与残留噪声。因此，本文提出了基于信息熵的EEMD方法抑制残留噪声。

信息熵通过描述随机变量的不确定性程度，对时间序列数据中的信息量进行度量[15]。信息熵定义为

式中：pδ为第δ 个 状态的概率，Nd为状态的总数。

为了抑制残留噪声，提取呼吸和心跳信号，将IMF分量按频率分为两类，第1类IMF分量的频率为0.1～0.5 Hz，第2类IMF分量的频率为0.8～2 Hz。计算第1类IMF分量的信息熵，找到呼吸分量，同时计算第2类IMF分量的信息熵，找到心跳分量。

对于第1类IMF分量，先对IMF分量做快速傅里叶变换，得到(f)(k=1,···,Nf) ，其中Nf为第1类IMF分量的总数。然后计算IMF分量的频谱中0.1～0.5 Hz之间的能量值的概率。

通过信息熵的大小分别对第1类IMF分量和第2类IMF分量进行排序，然后分别选择熵最小的IMF分量重构呼吸和心跳信号。

3 实验

3.1 实验设置

实测实验使用德州仪器公司(Texas Instruments,TI)的毫米波雷达AWR1843和AWR1642，这2个雷达分别设置为生物雷达和干扰雷达。雷达的具体参数如表1所示。实验数据通过与生物雷达相连的DCA1000数据采集卡传输到笔记本电脑。在实验中，志愿者位于生物雷达正前方，距离为0.7 m。干扰雷达斜对着生物雷达，距离为0.5 m。志愿者在腹部佩戴呼吸带(HKH-11C) 获取参考呼吸频率，并在手指上佩戴光体积描记器(Photoplethysmography, PPG)脉搏传感器获取参考心跳频率。

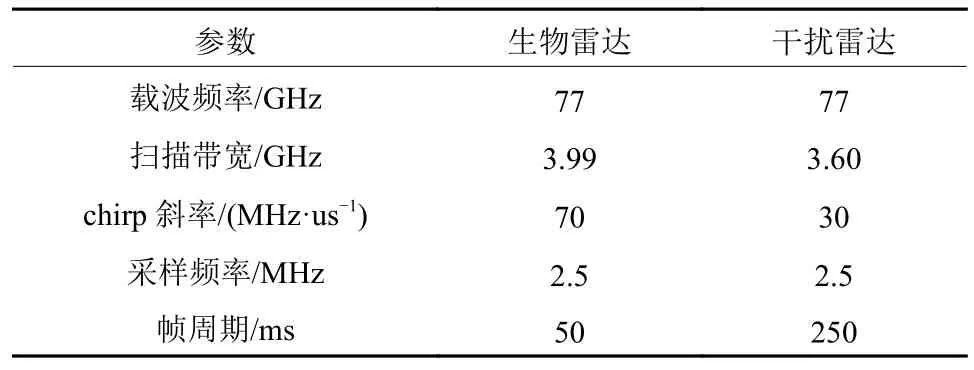
表1 生物雷达和干扰雷达的实测参数Table 1 Measured parameters of bioradar and interference radar

生命体征信号的信噪比和相对误差被用来评估所提出方法的性能。其中，信噪比定义为

3.2 实验结果

如图6(a)所示，无干扰时，差拍信号是幅度比较均匀的正弦波，在图6(b)的距离谱中可以观察到目标在0.711 m的位置，信噪比为3.076 8 dB。受到干扰后，如图6(c)所示，差拍信号的时域出现一小段能量很大的类脉冲干扰。在图6(d)的距离谱中，目标的底噪明显上升，信噪比为-15.371 6 dB，与无干扰的差拍信号相比，信噪比下降了18.448 4 dB。

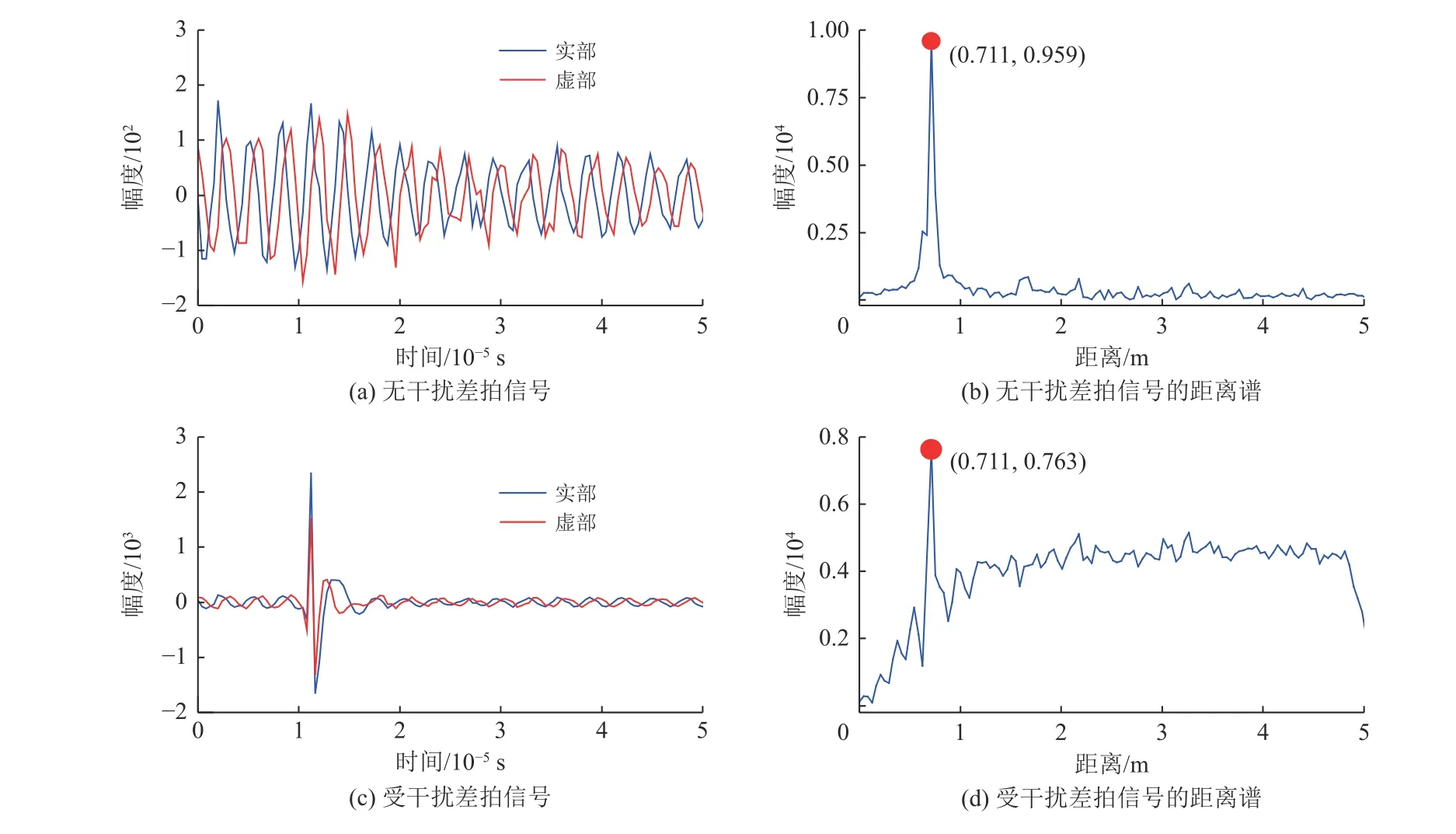
图6 干扰对差拍信号的影响Fig.6 Influence of interference on beat signal

为了抑制差拍信号的干扰，使用基于互相关的SSA方法对受干扰差拍信号进行分解和重构。如图7所示，互相关值最大的分量出现在第一个奇异谱分量中，因此选择这个分量重构差拍信号。重构的结果如图8(a)所示，差拍信号的类脉冲干扰被消除，其距离谱图8(b)中，底噪明显降低，信噪比为0.667 6 dB。与抑制干扰前相比，信噪比提高了16.039 2 dB。

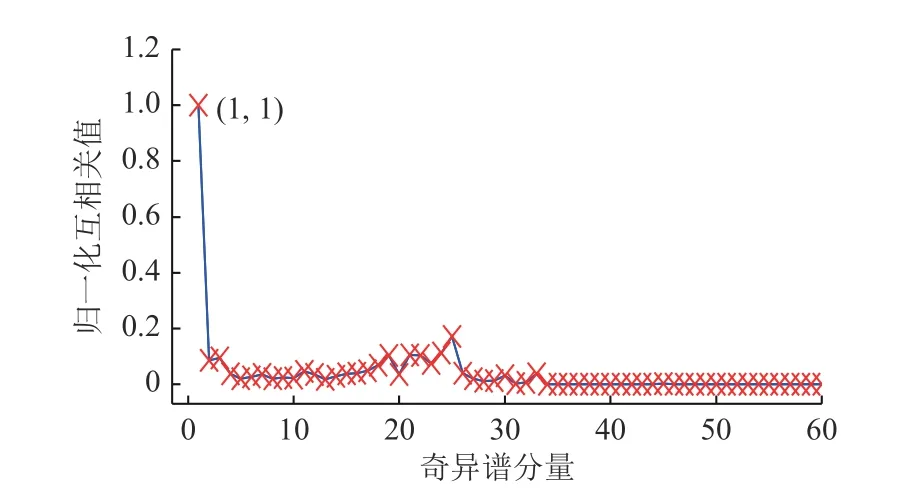
图7 受干扰差拍信号分解的分量与参考无干扰差拍信号的互相关Fig.7 Cross-correlation between the decomposed components of the interfered beat signal and the reference interferencefree beat signal

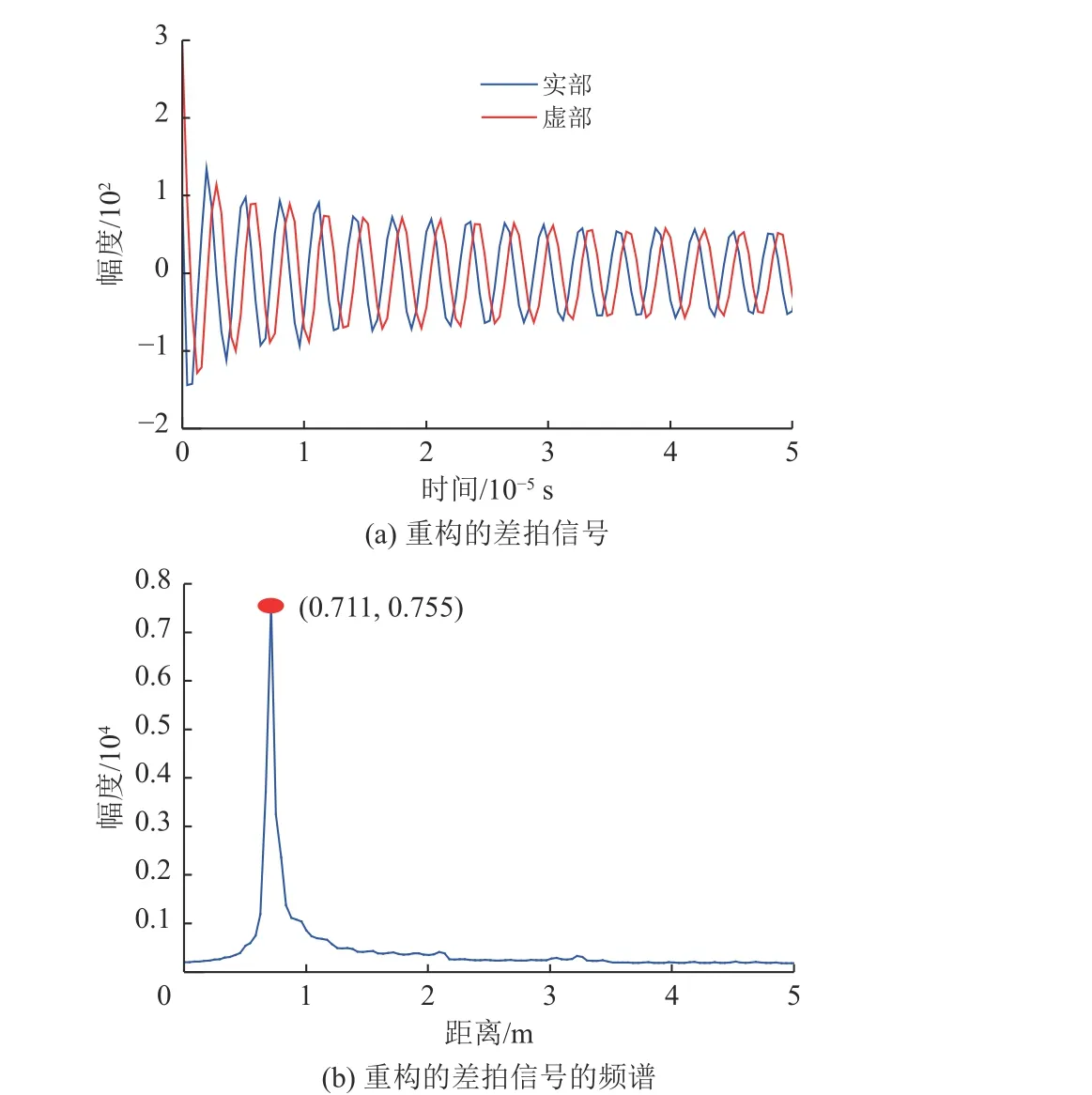
图8 抑制干扰后的效果Fig.8 Effect of interference suppression

抑制干扰前的生命体征信号频谱如图9(a)所示，呼吸频率0.313 Hz和心跳频率1.406 Hz处的频谱峰值被干扰带来的噪声淹没。呼吸的信噪比为-25.883 6 dB，心跳的信噪比为-24.247 8 dB。采用基于互相关的SSA抑制干扰后的结果如图9(b)所示，噪底明显下降。呼吸的信噪比为-13.891 1 dB，心跳的信噪比为-15.915 7 dB。与抑制干扰前相比，呼吸信噪比提高11.992 5 dB，心跳信噪比提高8.332 1 dB。

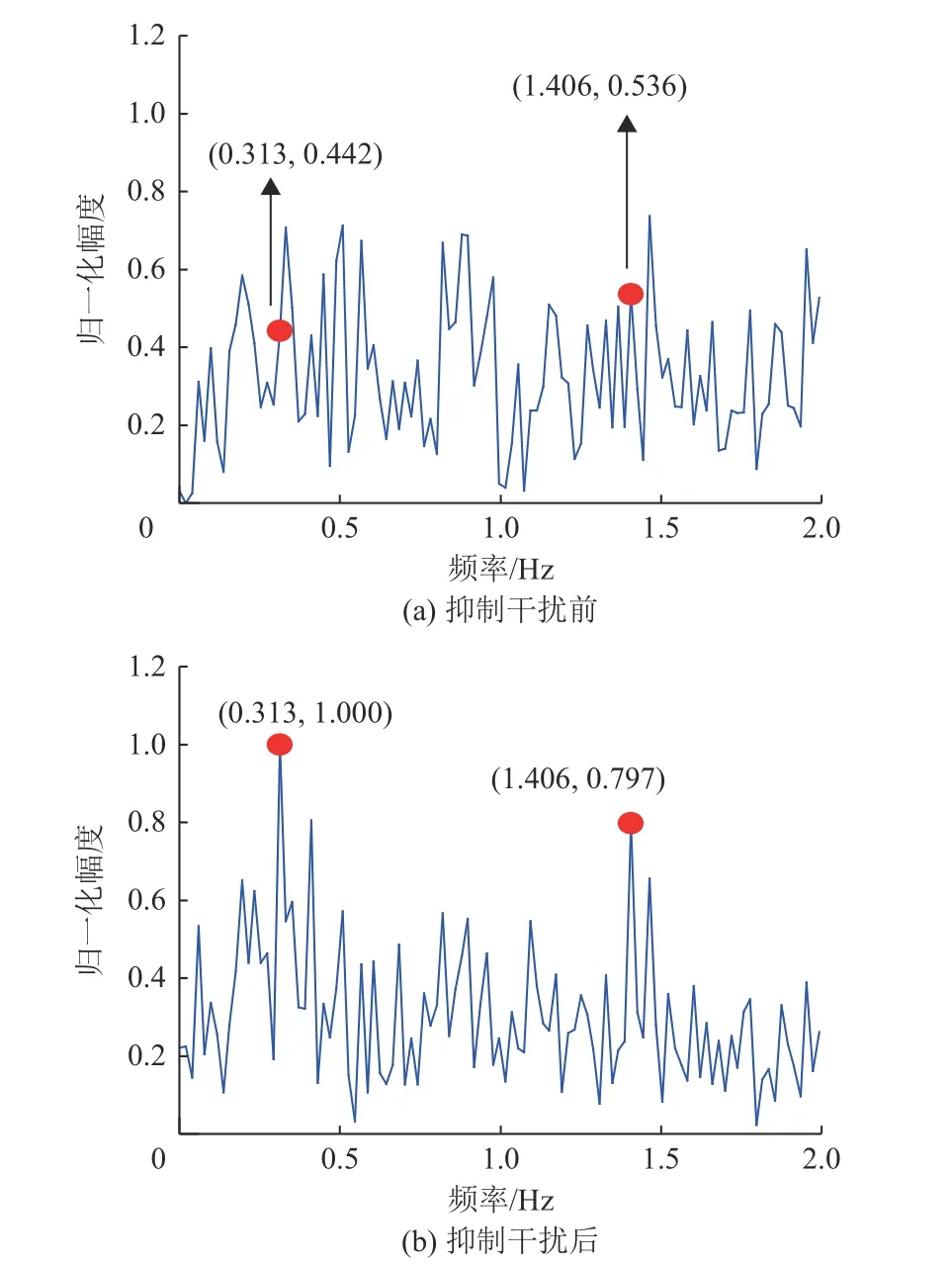
图9 生命体征信号的频谱Fig.9 Frequency spectrum of vital sign signal

因为抑制完干扰后，还有残留噪声，因此进一步对生命体征信号进行EEMD分解。如图10所示，相位差Δ φb(t)被分解为7个IMF分量和1个残差信号。

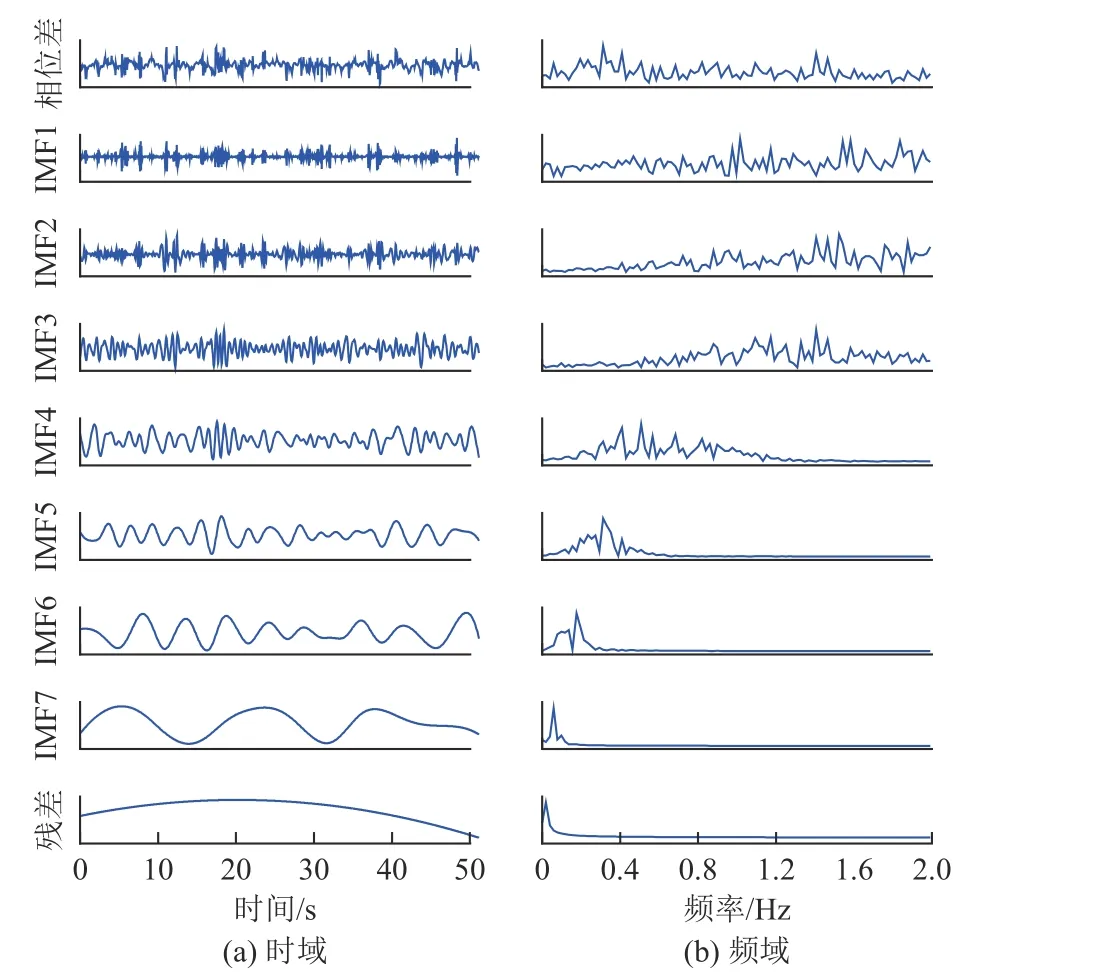
图10 对相位差进行EEMD分解的IMF分量及其频谱Fig.10 IMF components and frequency spectrum of EEMD decomposition of phase difference

其中IMF4～IMF6为第1类IMF分量，它们的信息熵分别为0.367 8、0.034 2和0.127 3。因为IMF5的信息熵最小，因此把IMF5选择为呼吸分量。IMF1～IMF3为第2类IMF分量，它们的信息熵分别为0.217 7、0.086 5和0.072 8。因为IMF3的信息熵最小，因此把IMF3选择为心跳分量。

重构后的呼吸和心跳信号的频谱如图11所示，生物雷达检测到的呼吸频率为0.313 Hz，呼吸信噪比为-5.100 2 dB。呼吸带检测到的呼吸频率为0.310 Hz，呼吸频率的相对误差为0.97%。生物雷达检测到的心跳频率为1.406 Hz，心跳信噪比为-10.138 2 dB。PPG脉搏传感器检测到的心跳频率为1.410 Hz，心跳频率的相对误差为0.28%。

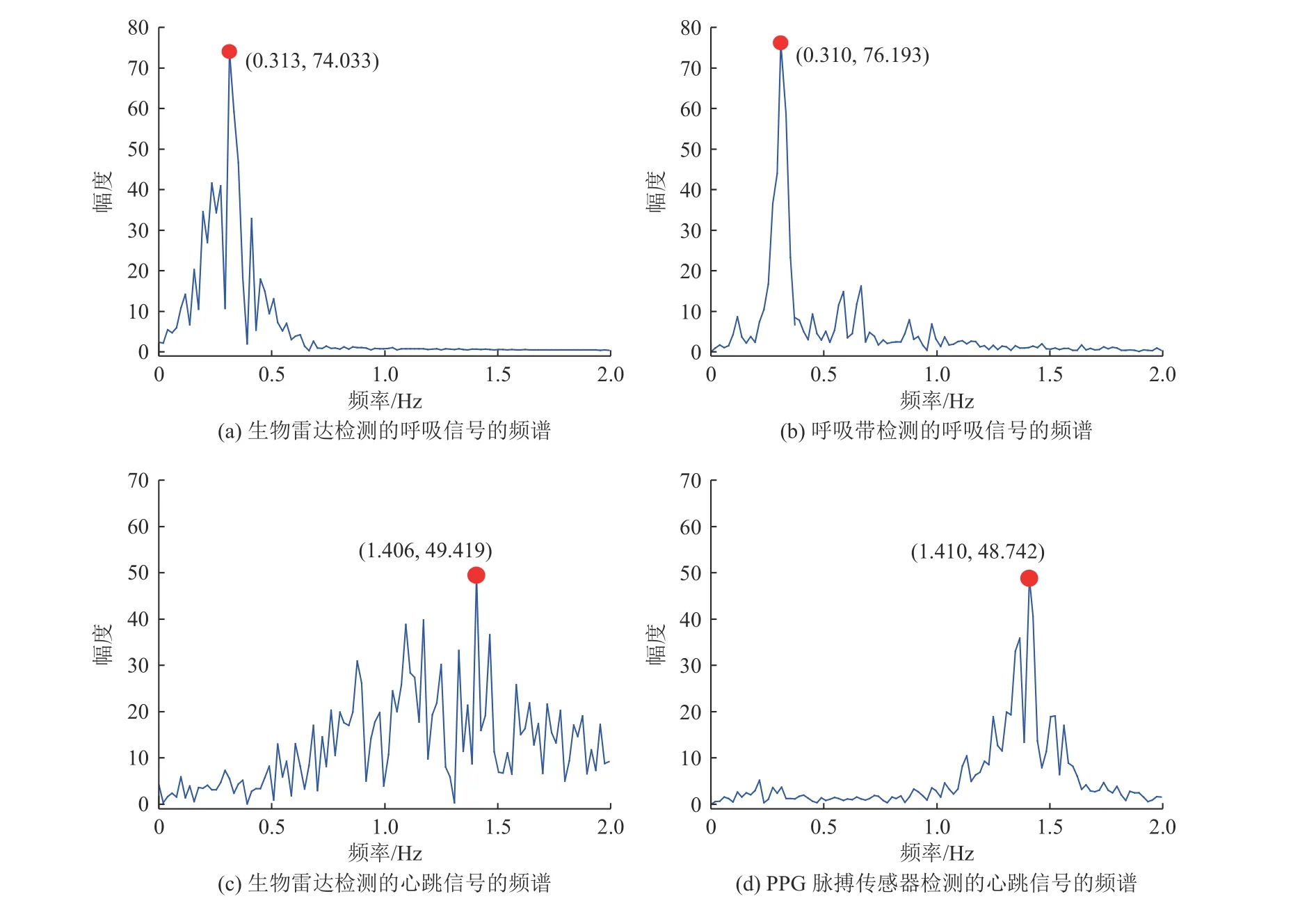
图11 生物雷达与呼吸带和PPG脉搏传感器的比较Fig.11 Comparison of bioradar with respiration belt and PPG pulse sensor

本文所提出方法与其他方法的对比如表2所示。当生物雷达受到干扰时，如果没经过干扰抑制处理，呼吸的信噪比为-25.883 6 dB，心跳的信噪比为-24.247 8 dB。文献[16]的IPELT-EEMD方法处理后的呼吸信噪比为-6.686 8 dB，心跳信噪比为-18.055 9 dB。而本文所提出方法处理后的呼吸信噪比为-5.100 2 dB，心跳信噪比为-10.138 2 dB。与没经过干扰处理相比，呼吸信噪比提高20.783 4 dB，心跳信噪比提高14.109 6 dB。与IPELT-EEMD方法相比，呼吸信噪比提高1.586 6 dB，心跳信噪比提高7.917 7 dB。实测实验的结果验证了本文所提出方法抑制干扰的有效性。

表2 与其他方法的性能对比Table 2 Performance comparison with other methods

4 结论

为了抑制毫米波雷达间的互扰对生物雷达的影响，本文提出了改进的SSA方法。通过相关性计算从受扰信号中选取人体反射信号分量重构差拍信号，抑制干扰影响，并进一步提出基于信息熵的EEMD方法抑制生命体征信号的残留噪声。实测实验结果表明，本文所提出方法能有效抑制干扰，提高呼吸和心跳信号的信噪比。下一步的工作主要是研究多目标的生命体征检测，以及抑制身体随机运动对生命体征检测的干扰。

（责任编辑：张玮欣 英文审核：熊荣斌）