刚毛翼拍合过程中复合运动对升力的影响

赵 磊,张树海,袁俊杰,张忠海,周 林,何广平

(1.北方工业大学, 北京 100144; 2.北京航天测控技术有限公司, 北京 100041)

0 引言

微型扑翼飞行器具有隐蔽性好、机动性强等突出优点,在军事侦察、搜救等领域拥有广泛的应用前景,受到了各国国防部门的高度重视[1]。飞行昆虫以其尺寸小、可悬飞等诸多优点成为了微型扑翼飞行器设计的重要仿照对象[2]。为了设计出高效、可靠的仿昆虫扑翼飞行器,学者们对中、大型昆虫的空气动力学进行了大量研究,对于中、大型昆虫的气动力机制有了较为深入的理解。然而,目前对于体长<2 mm、翼展1 mm左右的微小型昆虫的研究尚处于起步阶段,对其气动力机制的认识还相对有限[3]。微小型昆虫的振翅频率通常>200 Hz,其基于弦长的雷诺数(reynolds number based on chord length,Rec)约为4～60[4-5],并且许多微小型昆虫的翅膀上长有大量细长刚毛。刚毛翼的出现为飞行器的进一步微型化提供了全新的思路。

拍合运动(合拢-打开,clap-fling)是小昆虫常用的升力产生机制[6]。Clap是上行程末期昆虫的双翅在其背后相互靠近并绕前缘旋转合拢的过程,fling是合拢的双翅在下行程初期相互远离并绕后缘旋转打开的过程。Miller推测刚毛翼可通过clap-fling在Rec～10时获得较高的飞行效率[7]。Jones通过二维计算流体动力学(computational fluid dynamics,CFD)模拟发现,刚毛间隙的流体泄漏可减小左右刚毛翼在fling阶段所受阻力[8]。申研究了刚毛交叉对刚毛翼clap-fling过程中气动特性的影响[9]。吴分析了fling阶段刚毛附近的流场结构,并探讨了刚毛间的相互作用[10]。

由以上研究可知,clap-fling是刚毛翼在悬飞模式下的重要运动方式。目前已证实提高clap-fling中拍动与俯仰重叠时间占clap-fling总时间的比重(拍动-俯仰重叠率)能够有效提高实心扑翼的平均升力系数[7]。然而,拍动-俯仰重叠率对刚毛翼升力性能的影响目前尚不清楚。本研究中的主要工作是建立包含clap-fling运动的刚毛翼全扑动周期CFD模型,分析刚毛翼悬飞过程中的黏性效应,进而探讨不同拍动-俯仰重叠率对刚毛翼升力系数的影响。

1 刚毛翼几何及运动学模型

1.1 几何模型

刚毛翼昆虫翼尖附近的刚毛数量和刚毛长度通常明显高于其他区域[11],因此翼尖区域对升力贡献较大,通过截取翼尖附近的弦向截面(图1(a))能够近似反映刚毛翼的气动特性[12]。为此,本研究中根据吴提供的几何参数建立了刚毛翼的二维CFD简化模型[10]。其中,刚毛翼的二维简化几何模型如图1(b)所示。左右刚毛翼均由21根等间距的刚毛组成,其中每个圆代表一根刚毛的横截面;d为刚毛直径;g为相邻刚毛中心之间的距离;c为弦长,表示前缘刚毛中心至后缘刚毛中心之间的距离;左右刚毛翼的弦线在运动开始前相互平行,初始翼间距为W。以上几何参数的取值为:c=0.225 8 mm,d=0.005c,g=0.05c,W=0.2c。

图1 刚毛翼二维简化几何模型的建立Fig.1 Establishment of the two-dimensional geometric model of a pair of bristled wings

1.2 运动学模型

如图2所示,clap-fling中包含拍动和俯仰2种运动模式,常以俯仰运动的持续时间作为clap-fling的总时间。本文中采用以下考虑拍动-俯仰重叠率ξ的运动学模型[13]:

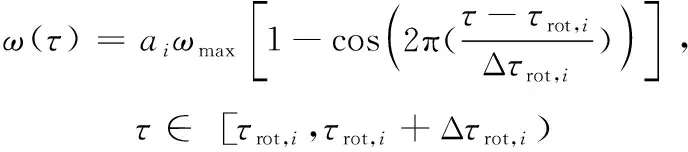
(1)

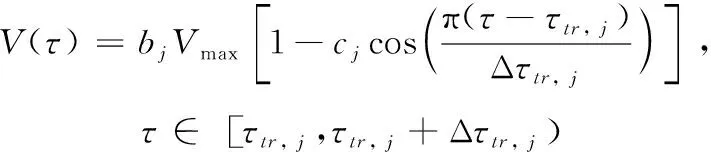
(2)

τtr,2=τrot,1+(1-ξ)Δτrot,1

(3)

τtr,6=τrot,4+(1-ξ)Δτrot,4

(4)

式(1)—式(4)中:ω为俯仰角速度;V为拍动线速度;τ为无量纲时间(τ=t/T,其中t为时间,T为扑动周期);i为俯仰角速度曲线的分段编号,i=1～6;j为拍动线速度曲线的分段编号,j=1～9;ωmax为俯仰角速度的最大值;Vmax为拍动线速度的最大值;ai为描述第i段俯仰角速度曲线的常数;bj和cj为描述第j段拍动线速度曲线的常数;τrot,i和Δτrot,i分别为第i段俯仰角速度曲线的起始时刻和所经历时间;τtr, j和Δτtr, j分别为第j段拍动线速度曲线的起始时刻和所经历时间;ωmax、Vmax、ai、bj、cj、τrot,i、Δτrot,i、τtr, j和Δτtr, j等参数的取值或表达式详见文献[13]。

图2 Clap-fling过程的二维示意图Fig.2 Two-dimensional diagrams of clap-fling

运动从下行程开始,首先进行fling;初始时刻双翼互相平行且翼间距最小。图3为ξ=50%时的无量纲速度曲线。

图3 ξ=50%时的全扑动周期无量纲速度曲线Fig.3 Dimensionless velocity profile in a complete flapping period at ξ=50%

2 刚毛翼CFD模型

2.1 控制方程与边界条件

刚毛翼的雷诺数和马赫数很小,属于典型的不可压缩层流问题,采用非定常不可压Navier-Stokes方程进行描述。

在悬飞模式下,刚毛翼流场的内边界为刚毛表面所构成的运动壁面,其运动规律由式(1)—式(4)确定,壁面处满足无滑移条件;外边界为距离刚毛翼足够远处的远场边界。

2.2 重要无量纲参数定义

升力系数CL定义为:

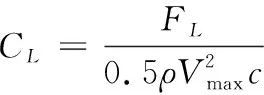
(5)

式(5)中:FL为升力,以竖直向上为正方向;ρ为流体密度;c为弦长。

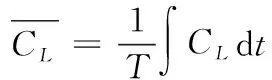
(6)

基于弦长的雷诺数Rec定义为:

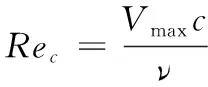
(7)

式(7)中:ν为流体的运动学黏度。

2.3 重叠网格方案

重叠网格的基本思想是:对于各个部件附近的流场区域分别划分部件网格,对整个流场区域划分背景网格,通过允许部件网格与背景网格之间以及不同部件网格之间相互重叠来简化网格划分过程,以便在部件周围生成高质量的结构网格和实现网格的参数化。重叠网格的基本流程如图4所示:① 通过挖洞处理找出不参与计算的洞单元;② 通过将更多单元转化为洞单元,将不同网格间的重叠区域最小化;③ 根据流场信息在重叠区域查找各套网格的插值接受单元与插值贡献单元;④ 根据插值接受单元与贡献单元之间的位置关系,插值计算出接受单元的流场信息,作为各套网格独立求解时的重叠边界条件;⑤ 根据重叠边界条件和物理边界条件对各套网格进行独立求解。

图4 重叠网格基本流程

本研究中,采用商业软件Fluent 2020R1进行刚毛翼的重叠网格划分和流场计算,其中重叠网格方案如图5所示。背景网格为半径为30c的圆形区域,内部划分结构网格,用于捕捉较远处的流场信息;部件网格为半径为2c的圆形区域,随刚毛翼刚性运动,内部划分高质量的结构网格,并在刚毛表面附近进行局部网格加密,用于捕捉刚毛附近的流场信息。针对以上网格系统,通过建立部件网格和背景网格的重叠边界,并对刚毛表面和刚毛翼部件网格施加运动速度,完成重叠网格的划分。

图5 重叠网格方案Fig.5 Overset grid scheme

2.4 数值求解算法及验证

速度项采用二阶迎风格式进行离散,时间格式采用一阶全隐式时间积分,求解算法采用压力-速度耦合求解算法。

为确保网格无关性,对网格总数为70万、90万和110万时的瞬时升力系数模拟结果进行了比较,比较结果如图6所示。由图6可知,3种网格数量下的升力系数非常相近,但考虑到总网格数量为110万时涡量等值线的光滑性较好,本研究中采用网格总数为110万的网格划分方案。

图6 网格无关性验证Fig.6 Grid independence verification

为验证所建立的刚毛翼二维CFD简化模型的有效性,针对Rec=10时的fling阶段,将本文中模拟得到的升力系数与吴模拟得到的升力系数[10]进行了比较,比较结果如图7所示。

图7 CFD模型验证Fig.7 Verification of CFD model

3 计算结果及分析

3.1 刚毛翼的黏性效应

在刚毛翼可能面对的低雷诺数范围内(Rec=10～80),分析了其黏性效应。图8为ξ=50%时不同雷诺数下刚毛翼升力系数随无量纲时间的变化。从图8可以看出,当Rec=10～80时,升力系数随着Rec的增大而明显减小。

为揭示雷诺数也即黏性效应对刚毛翼升力的影响机制,分析对比了Rec=10和80时的刚毛受力分布和刚毛翼流场。由于clap阶段、fling阶段和纯拍动阶段的情况相似,以下仅展示纯拍动阶段τ=0.24时刻的比较结果。图9-图12分别为Rec=10和80时的各刚毛升力系数及其压力与剪切力分量对比、速度场对比、涡量场对比和压力场对比。

图8 ξ=50%时不同雷诺数下升力系数 随无量纲时间的变化Fig.8 Variation of lift coefficient with dimensionless time at ξ=50% for various Rec

图9 Rec =10和80时纯拍动阶段τ=0.24时刻的 各刚毛升力系数及其压力与剪切力分量对比Fig.9 Comparison of the lift coefficient and its pressure and shear components of each bristle for Rec=10 and 80 at τ=0.24 during translation

由图9可知,Rec=10和80时刚毛表面的剪切力和压力均对升力有重要贡献,且各刚毛受力情况与其所在位置密切相关;同时,Rec=10时刚毛表面的剪切力和压差明显大于Rec=80时。

图10 Rec=10和80时纯拍动阶段τ=0.24时刻的 速度场对比Fig.10 Comparison of the velocity contour for Rec=10 and 80 at τ=0.24 during translation

图11 Rec =10和80时纯拍动阶段τ=0.24时刻的 涡量场对比Fig.11 Comparison of the vorticity contour for Rec=10 and 80 at τ=0.24 during translation

由图10和图11可知,Rec=10和80时刚毛间隙处均存在一定的正、反间隙涡。Rec=10时,刚毛间隙处整体流速较高,间隙涡相对较弱,说明刚毛间隙处的流体泄漏量较小;Rec=80时,高流速区域紧贴刚毛表面,在刚毛间隙处存在明显的低流速区域,流体与刚毛之间的相对运动速度较大,间隙涡明显增强,说明刚毛间隙处的流体泄漏量较大。由图12可知,Rec=10时刚毛左下方与右上方之间的压力差明显大于Rec=80时。综合以上分析可知,在刚毛翼最常见的悬飞雷诺数下(Rec=10),黏性效应较强,刚毛间隙泄漏明显减弱,使得刚毛翼内外侧连通性较差、压差较大,导致压力对升力系数的贡献明显大于Rec=80时。

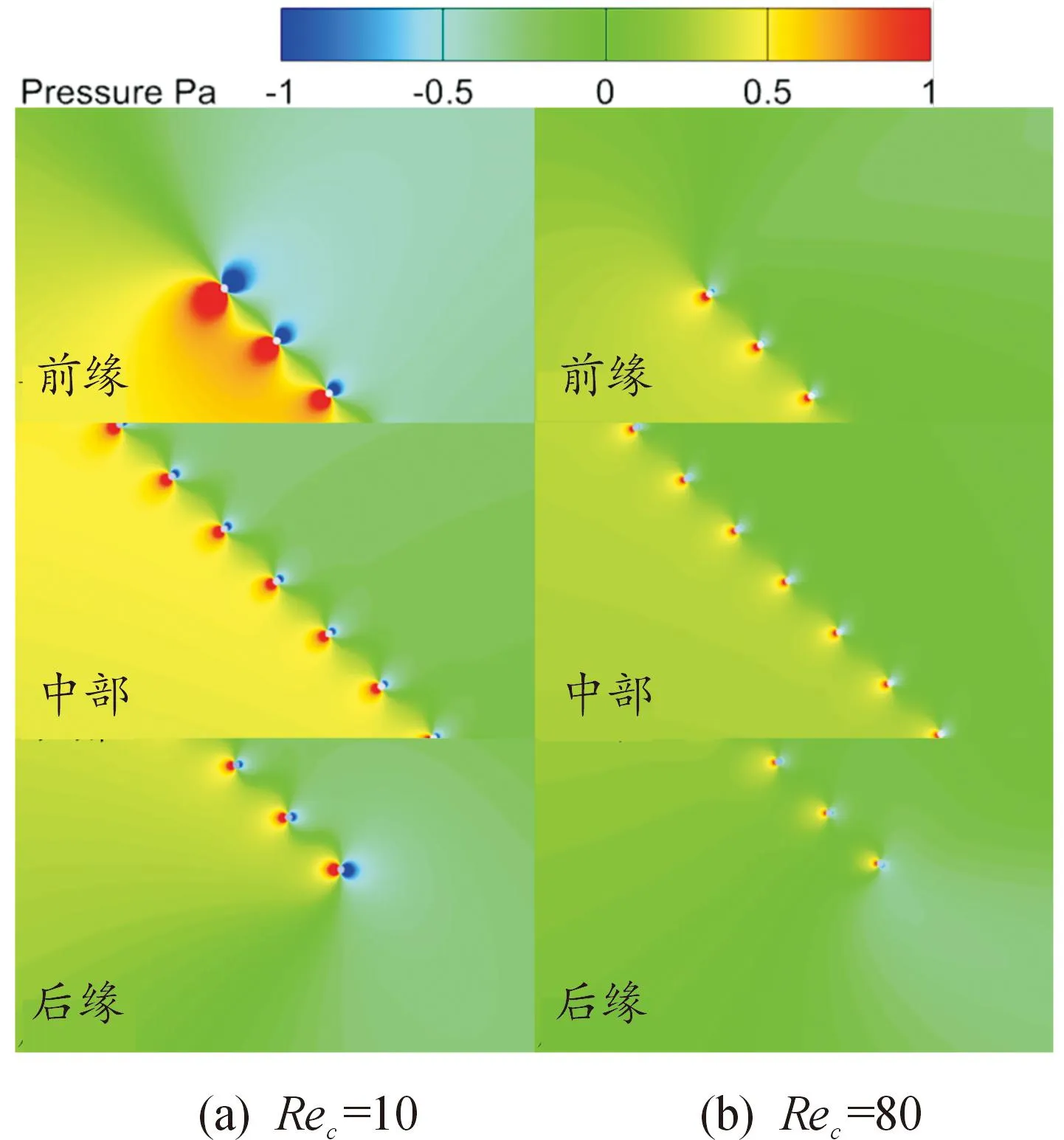
图12 Rec =10和80时纯拍动阶段τ=0.24时刻的 压力场对比Fig.12 Comparison of the pressure contour for Rec=10 and 80 at τ=0.24 during translation

为阐明Rec=10时剪切力对升力系数的贡献明显大于Rec=80时的原因,进行了以下量纲分析:

(8)

式(8)中:Cshear为刚毛表面的无量纲剪切力;μ为流体的动力学黏度;Vleak为流体通过刚毛间隙泄漏时相对于刚毛的平均流速;V∞为刚毛的绝对运动速度;Cleak表示刚毛间隙处的流体泄漏率,为雷诺数的函数,定义为Cleak=Vleak/V∞;Red为基于刚毛直径的雷诺数,定义为Red=ρV∞d/μ。

由式(8)可以看出,刚毛表面的无量纲剪切力Cshear总体上正比于Cleak/Red。在刚毛翼常见的刚毛间隙(g～10d)和可能面对的雷诺数(Rec=10～80,Red=0.043～0.35)下,根据两平行圆柱绕流理论[14],尽管间隙泄漏率Cleak随着Red的增大而增大,但其增加速率逐渐减小,因此Cleak/Red和Cshear随着Rec的增大而不断减小,Rec=10时刚毛表面的无量纲剪切力和剪切力对升力系数的贡献明显大于Rec=80时。

3.2 拍动-俯仰重叠率对升力系数的影响

为研究刚毛翼常见雷诺数下(Rec=10)拍动-俯仰重叠率ξ对升力系数的影响,在Rec=10下,分别模拟了ξ=0、25%、50%、75%、100%时的刚毛翼悬飞过程。其中,平均升力系数随拍动-俯仰重叠率的变化和不同拍动-俯仰重叠率下瞬时升力系数随无量纲时间的变化分别如图13和图14所示。

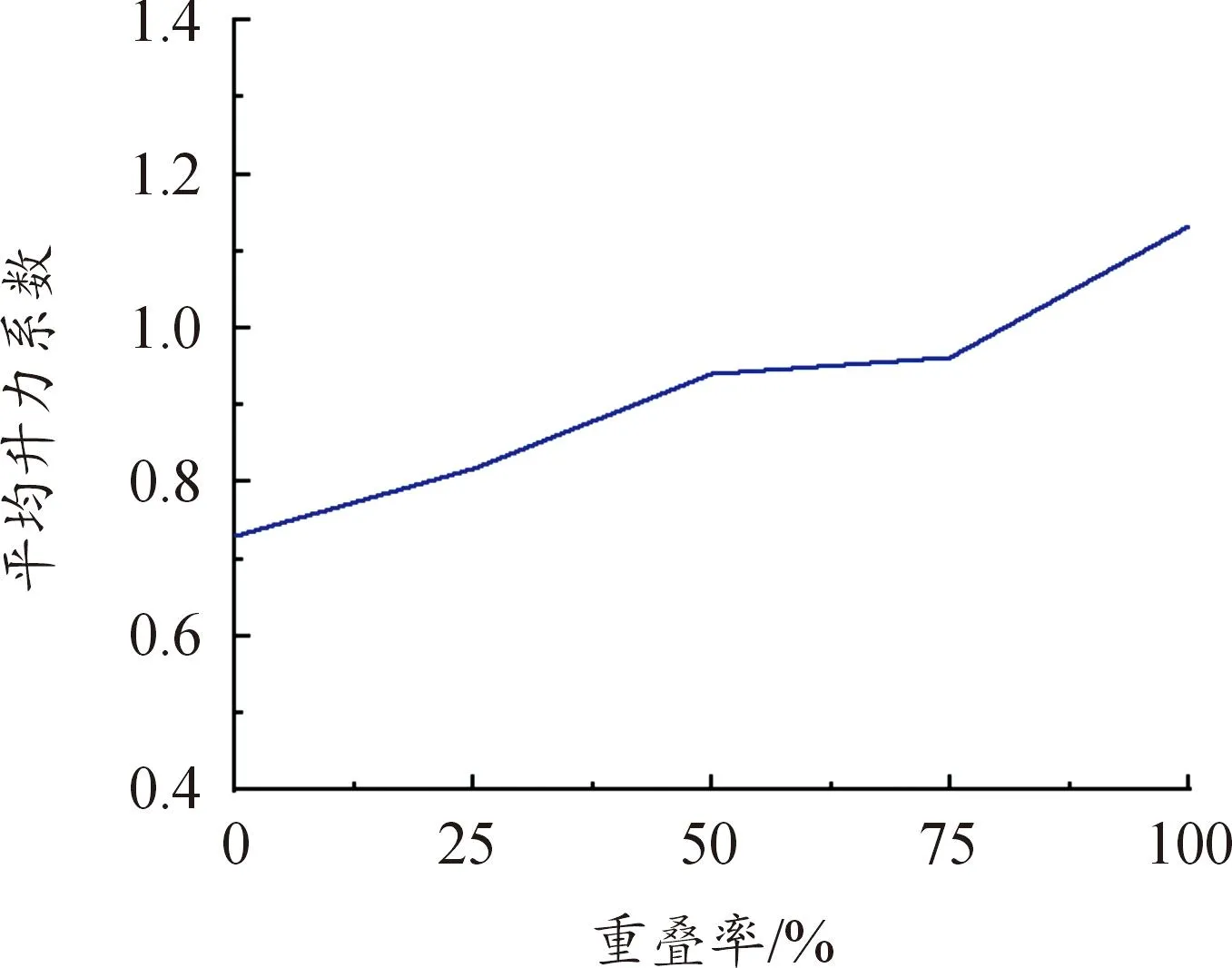
图13 平均升力系数随拍动-俯仰重叠率的变化

图14 不同拍动-俯仰重叠率下升力系数 随无量纲时间的变化Fig.14 Variation of lift coefficient with dimensionless time at various ξ

由图13可以看出,平均升力系数随着拍动-俯仰重叠率的增大而增大。结合图14可知,造成这一现象的主要原因在于:当clap和fling阶段的拍动-俯仰重叠率较低时(ξ=0和25%),会在clap和fling中期形成负升力峰值;随着拍动-俯仰重叠率的不断增大,以上负升力峰值逐渐消失(ξ= 50%),并最终转变为正升力峰值(ξ= 75%和100%)。

为进一步阐明上述负升力峰值的转变机制,选取fling阶段和clap阶段在ξ=0时的负升力峰值时刻τ=0.08和τ=0.9,分析对比了ξ=0和100%时的流场。由于流场左右对称,以下仅选取左翼进行分析。图15—图19分别为ξ=0和100%时在fling阶段τ=0.08时刻的升力系数及其压力与剪切力分量对比、速度场对比、涡量场对比、压力场对比以及剪切力竖直分量的分布情况对比。图20—图24分别为ξ=0和100%时在clap阶段τ=0.9时刻的升力系数及其压力与剪切力分量对比、速度场对比、涡量场对比、压力场对比以及剪切力竖直分量的分布情况对比。

图15 ξ=0和100%时在fling阶段τ=0.08时刻的 升力系数及其压力与剪切力分量对比Fig.15 Comparison of the lift coefficient and its pressure and shear components of each bristle for ξ=0 and 100% at τ=0.08 during fling

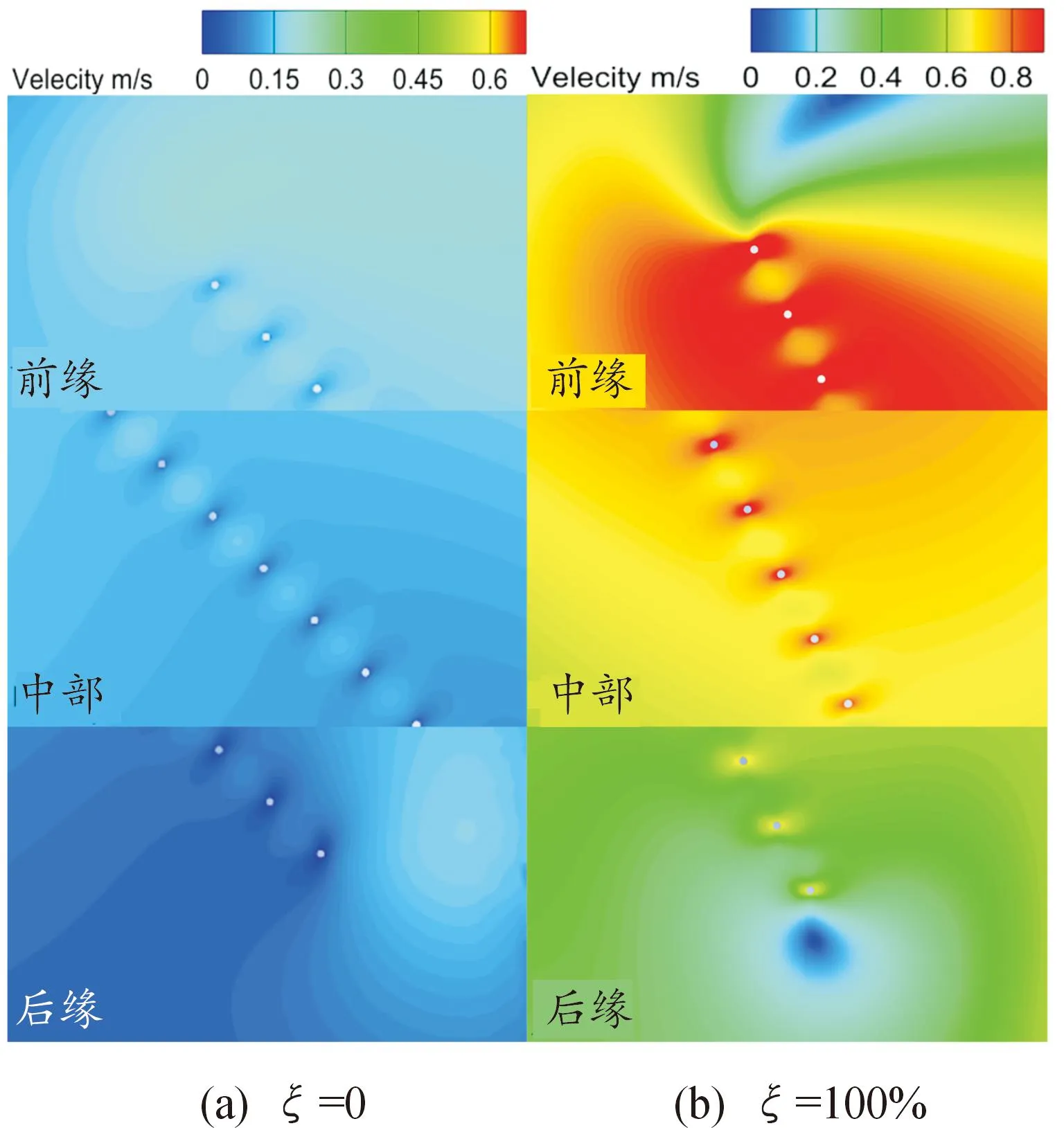
图16 ξ=0和100%时在fling阶段τ=0.08时刻的 速度场对比Fig.16 Comparison of the velocity contour for ξ=0 and 100% at τ=0.08 during fling

图17 ξ=0和100%时在fling阶段τ=0.08时刻的 涡量场对比Fig.17 Comparison of the vorticity contour for ξ=0 and 100% at τ=0.08 during fling

由图15—图18可知,当ξ=0时,流体通过刚毛间隙向左侧泄漏时分别在刚毛左下方和右上方形成了局部低压区和局部高压区,因此压差产生的合力指向左下方,对升力的贡献为负;而当ξ=100%时,流体通过刚毛间隙向右侧泄漏时在刚毛左下方形成了局部高压区,而在右上方形成了局部低压区,压差产生的合力指向右上方,对升力的贡献为正。此外,结合图15和图19可知,对于fling中期,当ξ=0时,刚毛左上方和右下方的剪切力竖直分量均为负,导致剪切力对升力的贡献为负;而当ξ=100%时,前缘附近刚毛剪切力对升力的贡献为正,而其他位置刚毛剪切力对升力的贡献为负。

图18 ξ=0和100%时在fling阶段τ=0.08时刻的 压力场对比Fig.18 Comparison of the pressure contour for ξ=0 and 100% at τ=0.08 during fling

图19 ξ=0和100%时在fling阶段τ=0.08时刻的 剪切力竖直分量分布情况对比Fig.19 Comparison of the vertical wall shear distribution for ξ=0 and 100% at τ=0.08 during fling

对于clap阶段中期(Rec=10),由图20可知,当ξ=0时,压力和剪切力对升力的贡献相当,且均为负值;随着ξ的不断增加,当ξ=100%时,压力仍对升力存在一定的负向贡献,但剪切力对升力的正向贡献更为显著,导致刚毛产生了明显的正升力。

图20 ξ=0和100%时在clap阶段τ=0.9时刻的 各刚毛升力系数及其压力与剪切力分量对比Fig.20 Comparison of the lift coefficient and its pressure and shear components of each bristle for ξ=0 and 100% at τ=0.9 during clap

由图21和图22可知,对于clap阶段中期,当ξ=0时,流场中的涡以刚毛间隙涡为主,流体通过刚毛间隙向右泄漏;当ξ=100%时,在拍动和俯仰运动的耦合作用下,左右翼加速闭合,在两翼之间产生的增压作用较为显著,使得流场中同时存在明显的逆时针前缘涡、顺时针后缘涡和明显强于ξ=0时的刚毛间隙涡,流体通过刚毛间隙向左泄漏。

图21 ξ=0和100%时在clap阶段τ=0.9时刻的 速度场对比Fig.21 Comparison of the velocity contour for ξ=0 and 100% at τ=0.9 during clap

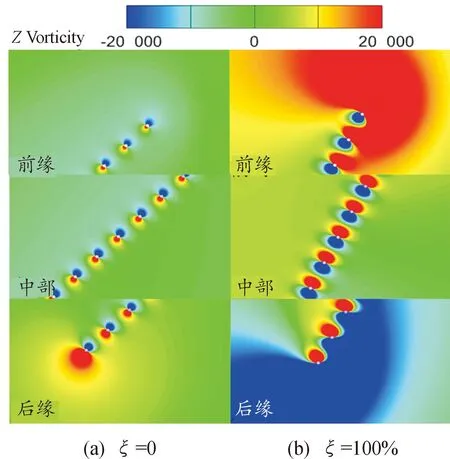
图22 ξ=0和100%时在clap阶段τ=0.9时刻的 涡量场对比Fig.22 Comparison of the vorticity contour for ξ=0 and 100% at τ=0.9 during clap

由图23可知,ξ=0时,刚毛左上方的高压区导致了负升力的产生;ξ=100%时,流体通过刚毛间隙泄漏时在刚毛右侧形成了局部高压区,且高压区随着刚毛位置远离前缘而向上移动,导致压力对大部分刚毛的升力贡献为负值。与此同时,由图24可知,对于clap中期,ξ=0时刚毛表面大部分区域的剪切力竖直分量为负值,导致剪切力对升力的贡献为负;而ξ=100%时刚毛表面大部分区域的剪切力竖直分量为正值,导致剪切力对升力的贡献为正。

图23 ξ=0和100%时在clap阶段τ=0.9时刻的 压力场对比Fig.23 Comparison of the pressure contour for ξ=0 and 100% at τ=0.9 during clap

图24 ξ=0和100%时在clap阶段τ=0.9时刻的 剪切力竖直分量分布情况对比Fig.24 Comparison of the vertical wall shear distribution for ξ=0 and 100% at τ=0.9 during clap

4 结论

1)Rec=10～80时,随着雷诺数的降低,黏性效应明显增强,刚毛间隙泄漏和刚毛翼内外侧连通性明显减弱,导致刚毛翼内外侧压差增大,压力对升力系数的贡献明显增强;与此同时,刚毛表面的无量纲剪切力同刚毛间隙泄漏率与雷诺数之比成正比,与雷诺数呈负相关,导致无量纲剪切力和剪切力对升力系数的贡献随着雷诺数的降低而明显增大。

2) 当拍动和俯仰运动无重叠时,clap和fling阶段中期的涡以成对出现且方向相反的刚毛间隙涡为主,流体泄漏方向与刚毛翼运动方向相同,泄漏过程中产生的剪切力和压力对升力的贡献为负,从而形成了明显的负升力峰值。

3) 当拍动-俯仰重叠率为100%时,clap和fling阶段中期的流体泄漏方向与刚毛翼运动方向相反,流场中同时存在明显的前缘涡、后缘涡和刚毛间隙涡;其中,clap阶段在流体泄漏过程中产生了明显的竖直向上剪切力合力,而fling阶段则在流体泄漏过程中产生了明显的竖直向上压差,导致clap和fling阶段的负升力峰值转变为正升力峰值,平均升力系数明显增大。