一种星载数模混合阵列结构及波束形成算法*
胡迪轩,朱立东,张勇,谢文轩,金世超,杨钰茜,费春娇
(1.电子科技大学通信抗干扰全国重点实验室,四川 成都 611731;2.中国空间技术研究院天地一体化信息技术国家重点实验室,北京 100094)
0 引言
随着信息与通信技术的发展,6G 网络将为用户提供更多维的体验。6G 网络将通过解决连接、覆盖、容量、数据速率和终端移动性方面的问题,实现全域覆盖的新一代网络体系架构,以提供更高的数据传输速率、更低的延迟、更大的连接密度、更低的能耗和更可靠的通信[1]。此外,6G 通过融合地面移动蜂窝网络与非地面网络,实现异构网络的全域服务连续性,从而达到真正的无缝覆盖。
星地融合技术是6G 网络中的重要部分,通过高中低轨卫星网络和地面移动通信网络共同组成了立体全覆盖的通信网,意图从协议、网络、体系等各方面实现天基网络和地面网络的互联互通与深度融合,从而实现用户的按需接入[2]。然而,随着卫星数量的逐步增多以及无线环境的日益复杂,星地通信面临着巨大的挑战[3]。在卫星通信系统中,相控阵技术被广泛应用于信号的收发处理。通过利用信号的空间分集增益以及高精度窄波束指向,相控阵技术实现了对信号的增强接收和集中发送[4]。这种演变不但需要对星地融合技术的进一步研究,也催生了对星载相控阵技术的更深入了解。
当前针对星载相控阵的研究已有很多,包括天线设计、阵列结构和波束形成算法等。针对阵列结构的研究主要以稀疏阵列和多级阵列为主,可以有效降低大规模阵列复杂度,通过适当减少阵元数量或是划分阵列结构实现多级阵列,达到与标准阵列相似的性能[5]。由于子阵划分方式多变,根据不同的指标和环境所设计的子阵均有别[6-7]。复杂且随机的子阵划分虽然能带来良好的性能,但是对于子阵后的硬件结构设计有较高要求,甚至有可能无法实现,因此当前仍多采用均匀划分子阵的方式[8],该方式直观且易于部署。
波束形成算法也可以分为自适应波束形成算法[9]、随机优化波束形成算法[10]以及常规波束形成算法,经典的最小方差无失真响应(MVDR,Minimum Variance Distortionless Response)是一种比较常见的自适应波束形成算法。在此基础上,将单一约束的MVDR 扩展到多约束条件,即线性约束最小方差(LCMV,Linearly Constrained Minimum Variance)算法。这一算法通常需要较多的训练数据和较大的求逆运算。随机优化波束形成算法则以启发性算法为主,包括遗传算法[11]、粒子群算法[12]等,但是这些算法收敛速度较慢,通常在分钟级,无法满足低时延的要求。常规波束形成算法则基于解析方法,研究波束的数学关系,最终获得闭式的解析解,如基于FFT 的波束形成算法等[13]。
1 阵列结构设计
为降低运算复杂度和硬件成本,本文考虑一个两级数模混合阵列结构,该结构示意图如图1 所示,其中第一级为模拟子阵列,第二级为数字子阵级阵列(也称为超阵)。模拟子阵列使用模拟权值,量化精度有限,且移相调整速度较慢,对于产生实时自适应抗干扰的波束方向图有困难。数字子阵级阵列采用数字权值,调整灵活且实时性强,是当前相控阵多采用的结构[14]。

图1 数模混合架构阵列示意图
图1 中,w表示接在子阵后的模拟权值,可以表示成有限位数模拟移相器和有限位数模拟衰减器的组合,即。将每一个子阵列的接收数据合并到一路数字信号后,最终在数字域进行波束处理,W表示数字权值,数字移相器位数通常较高,可以认为在量化效应在16 bit后对于阵列波束的损失忽略不计[15]。
以上结构既保证了基本的阵列功能又降低了算法复杂度和硬件成本,在数字域拥有灵活的波束形成空间,是目前广泛运用的形式[16]。本文采用阵列规模为30×30的均匀矩形阵列(URA,Uniform Planar Array),阵列均匀划分成5×5 个子阵,其中子阵大小为6×6 的URA。
星载相控阵的工作频段通常较高,阵元间距较短,会出现明显的天线耦合效应影响波束性能。为减弱子阵相邻天线之间的电磁耦合效应[17],降低系统复杂性、硬件成本并提高系统灵活度,学习稀疏阵列的划分方式,但不再是保持互耦环境不变,而是降低馈电数量,本文子阵列的设计采用50%稀疏馈电的方式[18]。如图2 所示,其中每一个方格表示一个天线单元,每一个红点表示一个馈电单元。这种结构表明,在子阵中,根据馈电关系,每两个阵元共用一个模拟权值。该结构设计可以进一步降低硬件成本,但是对于波束形成的算法提出了要求。稀疏馈电的算法设计将在下一节提及。
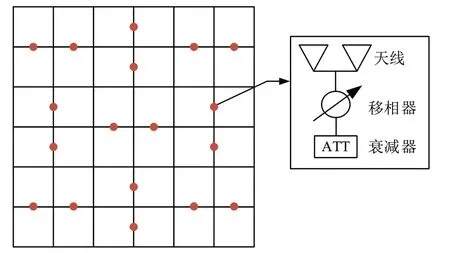
图2 子阵馈电结构示意图
根据阵元的等效相位中心推算[19],超阵的每一个阵元都是某一子阵的几何中心。如图3 所示,超阵结构实际上是一个等效的大间距稀疏URA,其等效的阵元间距达到了6 倍子阵阵元间距。

图3 超阵等效示意图
2 波束形成算法设计
2.1 子阵波束形成算法
对于50% 稀疏馈电子阵结构,每两个阵元共用一个模拟权值,因此存在一个变换矩阵,其中M表示阵元个数,NS表示馈电的个数。T 由0、1 组成,若按列顺序从上到下对阵元进行编号,则T 的每一列表示一个稀疏馈电与阵元的关系,若馈电作用于某阵元,则对应行位置的矩阵元素置1。因此T 的每一列有且仅有两个1,其余元素均为0。即输入馈电权值与输入给阵元的权值之间存在一个关系:
为了使稀疏馈电的权值在某种意义下逼近100% 馈电的权值,本文考虑采用最小二乘(LS,Least Square)方法,即有如下问题:
针对此最小二乘问题,使用拉格朗日乘子法,可以得出闭式解:
根据式(3) 获得的稀疏馈电权值满足最小二乘意义下对100% 馈电权值的逼近。
2.2 超阵波束形成算法
本节使用的阵列结构及其参数空间如图4 所示,其中θ表示方位角,表示俯仰角。
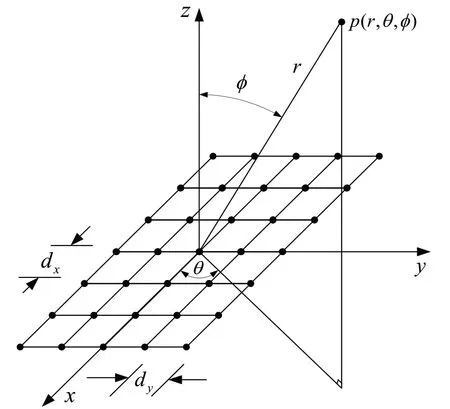
图4 阵列结构及参数空间示意图
考虑在波束到达角已知的情况下设计波束形成,使用LCMV 算法和LS 算法。同时,考虑存在空域干扰信号的情况。由于模拟子阵部分进行干扰零陷生成会受到稀疏馈电与量化效应的影响,使得零陷深度变浅或位置偏移,因此在超阵进行数字空域干扰抑制成为合理的选择。
对于LCMV 算法,设计优化问题如下:
当约束矩阵为一个矢量时,即单个无畸变约束,LCMV 算法退化为MVDR 算法。
LS 算法根据逼近目标设置不同,略有差别,本文中对波束方向图进行逼近,对于由全向天线组成的阵列,其波束方向图为,所以有如下问题:
其中Wd表示期望波束方向图的加权值,该优化问题希望在逼近期望权值的同时实现对干扰来向信号的零陷生成。
使用拉格朗日乘子法获得式(7) 的解为:
2.3 全阵波束合成
本节对两级阵列结构输出的波束方向图进行合成,获得最终30×30 URA 的波束方向图。根据多级子阵合成理论[20],完整阵列的波束方向图表示为:
其中下标Full 表示完整阵列,m表示第m个子阵,p表示第p个超阵;M表示子阵的阵元个数,P表示子阵的个数,也即超阵的等效阵元个数;wmp表示第p个子阵的第m个阵元的模拟权值,WP表示第p个子阵后所接的数字权值。
如果每个子阵内所加的模拟权值相同,则式(9) 可以化简为:
其中Gsub表示子阵的波束方向图,Gsup表示超阵的波束方向图,在分贝尺度下表示为和的形式。
接下来对波束方向图合成的理论模式进行分析。由于URA 实际上是由多个均匀线阵(ULA,Uniform Linear Array)所构成的,因此在方位角或俯仰角切面上波束方向图表示为ULA 的特性,出于方便考虑,下文的理论推导从ULA 切入。
对于一个以坐标原点对称的N 阵元ULA,其波束方向图可以表示为:
对于本文设计的子阵,其阵元间距为λ/2,则超阵的等效阵元间距达到了3λ,根据式(13),计算其栅瓣位置如下:
其中D表示超阵的阵元间距,m表示任意的非零整数取值,以说明栅瓣的周期性,因此在可视区域内将出现至多6 个栅瓣。
计算子阵波束方向图的零点位置如下:
观察式(13) 和式(14) 可知,在本文划分的两级阵列架构下,超阵的栅瓣位置与子阵的零点位置一一对应,在最终波束合成时,由于超阵阵元间距过大带来的栅瓣现象将被子阵零点抑制。
3 性能分析
为了验证本文所提的数模混合阵列结构,模拟了工作在Ku 波段的有限视场角(LFOV,Limited Field of View)星载阵列。对不同层级的阵列进行分析,讨论了阵列的波束方向图性能和抗干扰性能。
3.1 子阵波束方向图
本节对2.1 节提出的子阵波束形成算法进行验证,仿真参数设置如表1:

表1 子阵仿真参数
使用子阵的LS 算法获得50%稀疏馈电下的权值,根据式(2),的产生方式由传统相移波束成型器(CBF,Conventional Beamformer)产生,即只对阵列有指向的要求。取指向角度的俯仰角切面,获得的波束方向图如图5 所示,可以观察到由于50%的稀疏馈电和6 bit 量化效应的影响,LS 方向图与CBF 的理想方向图出现略微偏差,包括零点的偏移和旁瓣的抬升,但是指向位置、主瓣形状基本保持正确。

图5 子阵俯仰角切面波束方向图
3.2 超阵波束方向图
本节对2.2 节提出的超阵波束形成算法进行验证,大部分仿真参数不变,调整参数如表2 所示。其中,由于期望信号与干扰信号来向不同,拥有不同的信道环境,因此分别设置信噪比和干噪比,并设置一个较大的干信比表示点频干扰压制的情况。

表2 超阵仿真参数
使用LS 和LCMV 算法分别生成波束方向图,其中信号快拍用于LCMV 的信号自相关矩阵估计。分别产生指向方向和干扰方向的两个俯仰角切面图如图6 所示,可以观察到在指向方向的俯仰角切面中,LS 和LCMV 算法均保持了基本正确的指向,但是出现了一定偏移;在干扰方向的俯仰角切面中,LS 和LCMV 算法在干扰位置正确地生成了零陷,并且方向图波形基本保持一致。
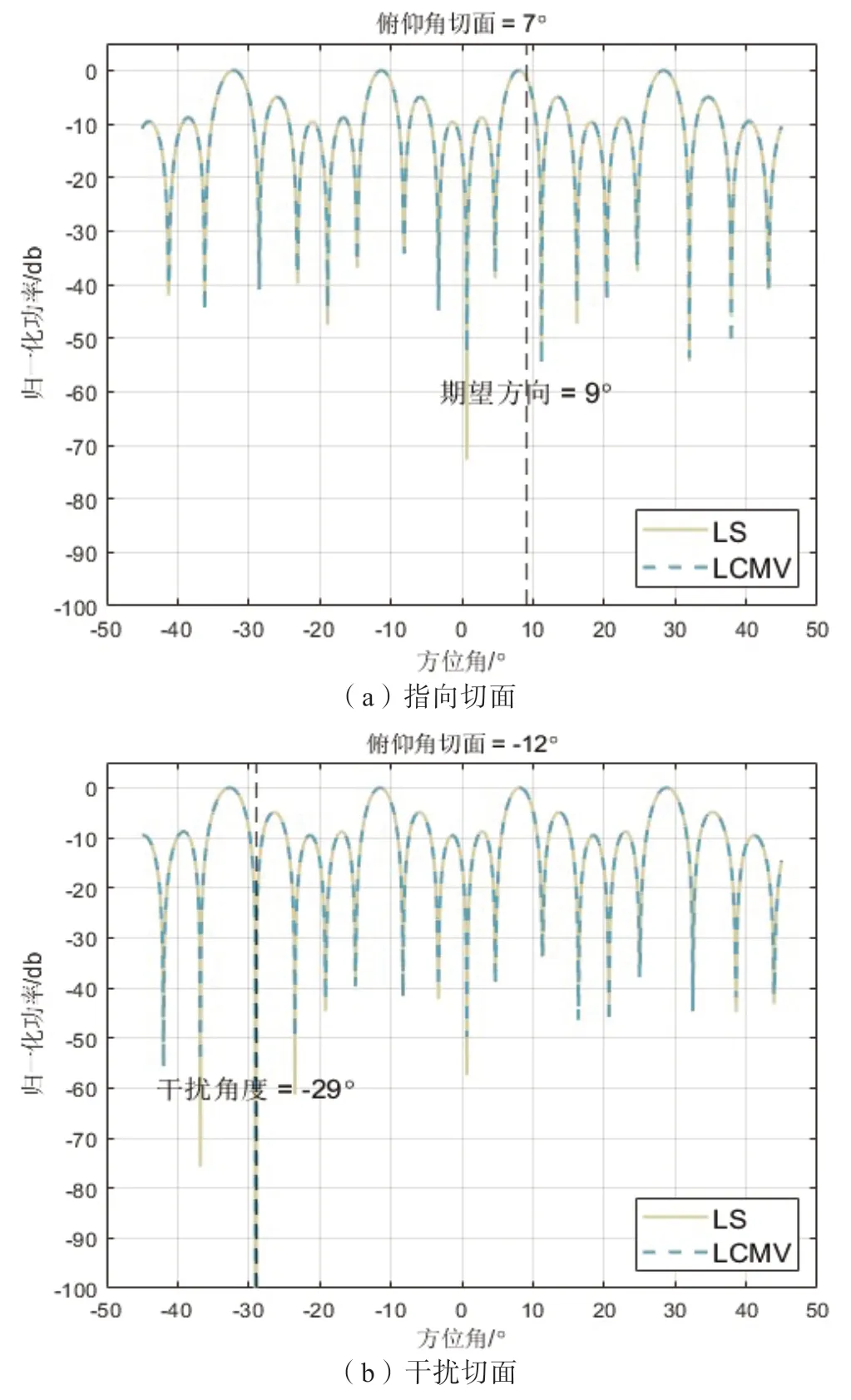
图6 超阵指向和干扰俯仰角切面方向图
进一步验证超阵波束方向图与理论推算的差异,在式(13) 中推算每个栅瓣距离阵列指向的角度约为19.5°,仿真结果约为20.3°。在干扰切面上,LS 和LCMV 算法分别形成的零陷深度为-321.8 dB 和-301.2 dB,这是只有高位数高精度数字域零陷生成才能达到的深度,其中LS 拥有比LCMV 更深的零陷深度,能够抑制更高功率的干扰。考虑到硬件实现误差、信号角度估计不精确等问题,可以放松约束,设置零陷约束参数为接近0 的定值而不是0,从而获得更宽的零陷并降低算法敏感度。
3.3 全阵波束方向图
首先验证2.3 节推算的超阵栅瓣与子阵零点位置结果,仿真如图7 所示,其中子阵波束形成算法采用2.1 节的设计,超阵采用LCMV 算法。可以观察到子阵零点位置确实地与超阵栅瓣位置重合。
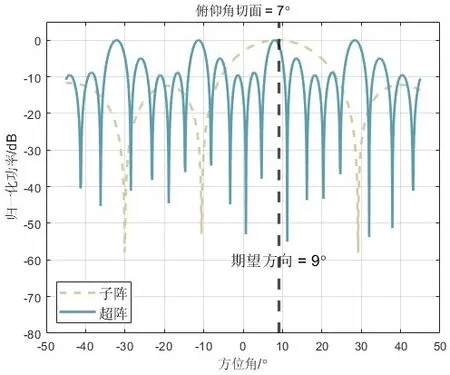
图7 子阵和超阵的零点和栅瓣位置
利用图7 给出一种波束合成的解释:符合标准半波长间距的子阵列所形成的波束拥有较宽的主瓣宽度,而超阵拥有较窄的主瓣宽度,因此两级波束形成实际上是先形成一个指向较宽的波束,随后利用更细的波束在上一级主波束内选取更精确的角度。
最终产生的完整阵列波束方向图如图8 所示,该图给出的是指向方向和干扰方向的俯仰角切面图。切面指向正确,且根据栅瓣零点对消原理,阵列的栅瓣得到了部分抑制,但是旁瓣高度仍旧较高。在干扰切面上,零陷生成的位置正确,且零陷深度足够。图9 给出了全阵的三维波束方向图,左图直角坐标系干扰和指向切面的交点分别表示零陷和指向位置,右图给出了阵列波束方向图在极坐标空间中的形式。
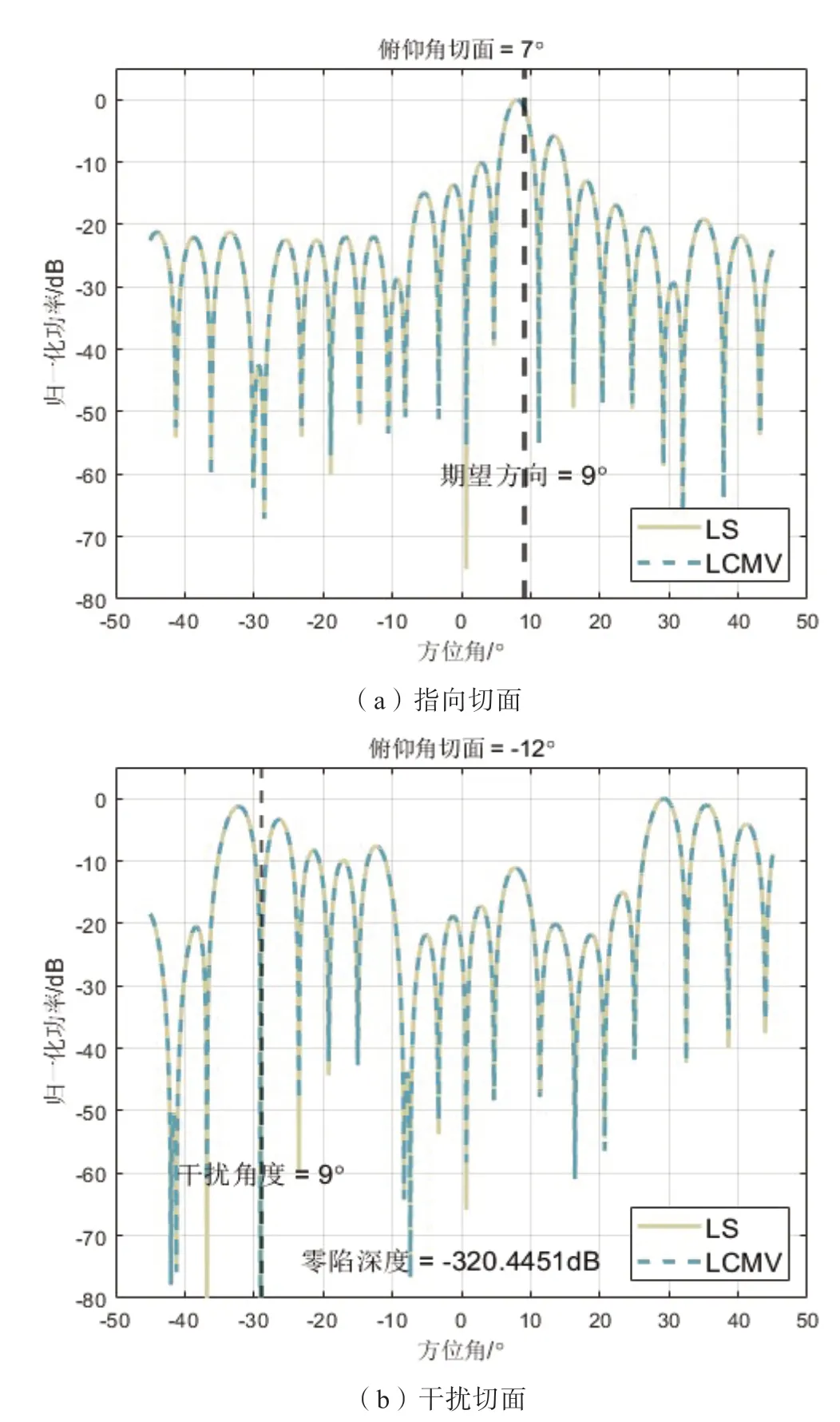
图8 全阵指向和干扰俯仰角切面方向图。
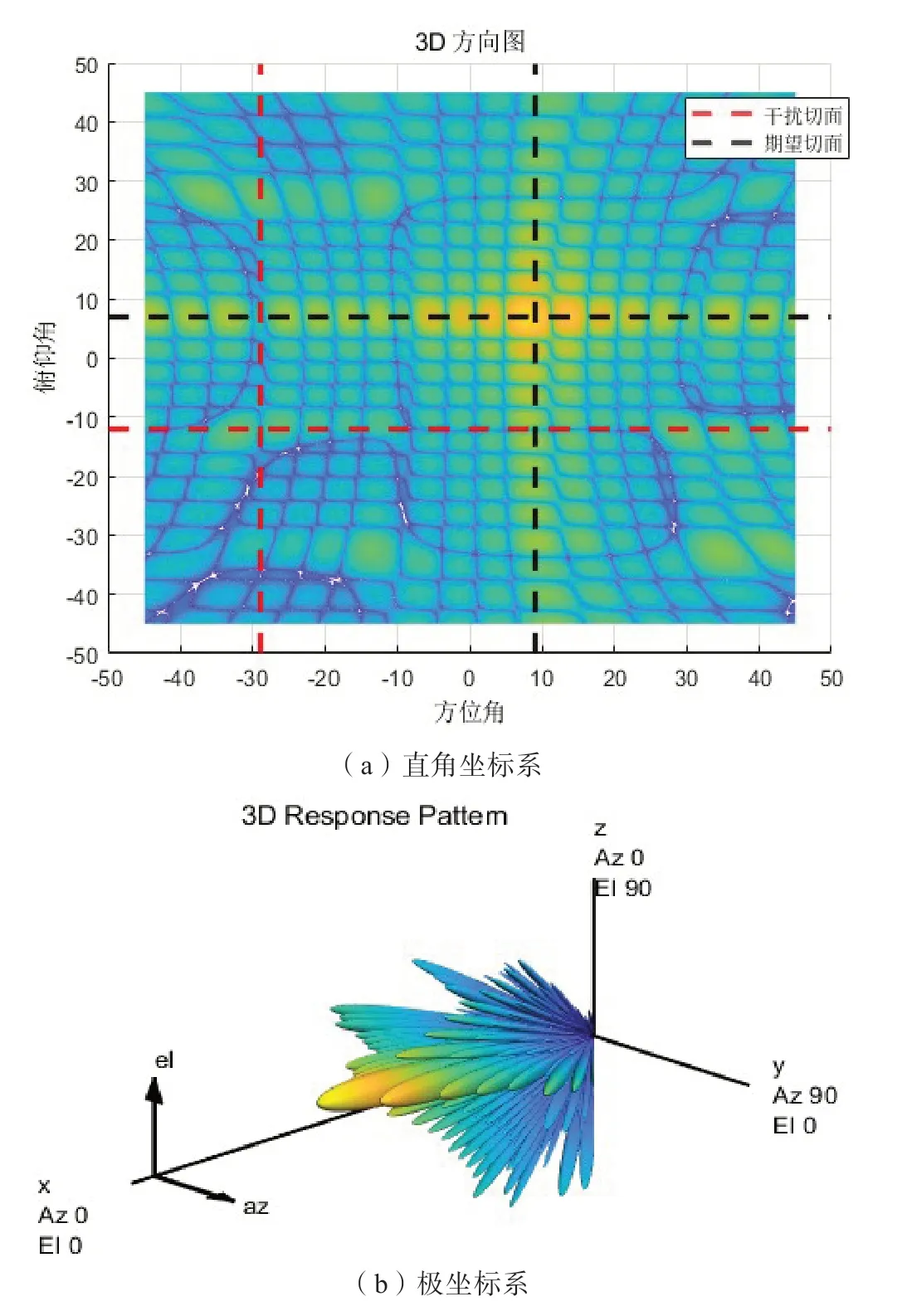
图9 全阵3D波束方向图
3.4 抗干扰性能
最后对LS 和LCMV 算法的抗干扰性能进行验证,仿真参数设置同表2,只需要将阵列扩展到完整30×30 URA的大小,采用BPSK 信号进行误码率(BER)性能测试,信号点数为5×105,并设置SNR 范围为-50:25 dB,步进为1 dB。最终获得的BER 曲线如图10 所示,观察到LS与LCMV 算法的BER 性能几乎一致,而没有进行零陷生成的CBF 算法无法抑制干扰,这导致其性能最差。根据阵列增益理论推算,本文设计的阵列结构所具有的最大阵列增益为:
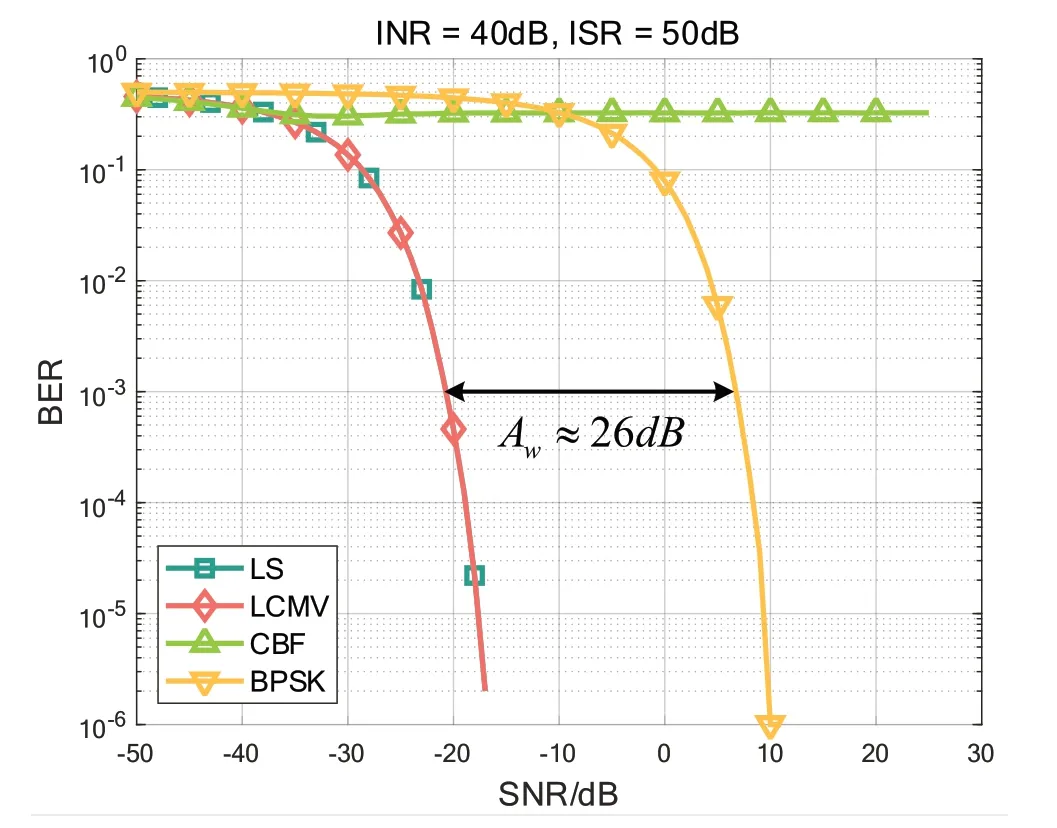
图10 抗干扰BER性能曲线
因为在LS 和LCMV 算法中均进行了空域干扰抑制,因此获得了约26 dB 的阵列增益,与理论最大增益较近,符合预期。
相较于LCMV 算法,LS 算法减少了求逆运算,算法复杂度有一定降低且不依赖于快拍信号而是利用已知的到达角进行处理。但是LCMV 算法能提供更灵活的约束,在信号估计足够的情况下,波束方向图的性能通常更优。考虑到两算法的BER 性能接近,需要结合更多资源分析使用哪一种算法。
4 结束语
针对现在星地融合网络对于高宽带信号、大规模星载阵列的要求以及卫星易受到干扰的情况。本文提出了一种数模混合的大规模星载相控阵结构,并给出了设计方案,涵盖了稀疏馈电子阵设计和大间距超阵设计、子阵和超阵波束形成算法设计,随后从理论上推导了子阵零点与超阵栅瓣的位置关系,验证了两级阵列架构的可行性。通过仿真验证了阵列结构以及波束方向图,LS 算法和LCMV 算法均能获得优异的抗干扰性能,从而提高了星载阵列的稳健性和对干扰的抵抗能力。

