基于直流电流瞬时微分的特高压直流分层接入系统非故障层换相失败预防控制策略

王渝红，李元琦，廖建权，陈立维，赏成波

（四川大学 电气工程学院，四川 成都 610065）

0 引言

随着我国高压直流工程的建设，直流落点在华东、华南地区聚集，已形成多馈入直流系统，直流系统发生换相失败的风险进一步增加［1⁃3］。为提高受端交流系统电压支撑能力，引导潮流合理分布，文献［4］提出了特高压直流分层接入系统拓扑结构，即受端分别接入500 kV和1 000 kV交流系统。分层接入系统已在锡林浩特—泰州、扎鲁特—青州、上海庙—山东、呼伦贝尔—皖南等工程中应用［5］。

与单层多馈入直流系统相比，分层接入系统可显著提高受端系统的短路比，提高交直流混联系统的稳定性［6］。在控制方式和稳定运行方面，文献［7］针对实际工程的直流控制系统，分析了分层接入下特高压直流控制系统与普通特高压直流系统的差异，提出了分层接入系统逆变侧的层次架构。文献［8］研究了吉泉直流分层接入华东电网后的稳定特性，并提出了一种满足热稳定和功角稳定约束的安全控制策略。文献［9］提出了分层接入系统短路比的定义，该指标可直接判断分层接入下交直流系统的强弱，并在实际系统中进行验证。

目前针对传统直流输电系统换相失败的研究有增加无功补偿设备、改变换流器拓扑、改进直流控制系统等。文献［10］和文献［11］分别对静止无功补偿器和同步调相机的优化配置模型进行求解，以降低换相失败的发生概率，但增加了投资成本；文献［12⁃13］从改进换流器拓扑结构出发，提出可显著降低换相失败发生概率的新型换流器拓扑；文献［14］和文献［15］分别设计改进低压限流控制器（voltage dependent current order limiter，VDCOL）和定关断角控制器，使换流器提前触发，此类方法无须增添额外设备且易于实现，是当前研究如何抵御换相失败的重点。

由于受端接入不同电压等级的交流系统，分层接入系统非故障层换流器可能因为层间耦合作用而发生换相失败，针对该系统换相失败的抑制还需进一步研究。文献［16］指出非故障层换相失败预防控制（commutation failure prevention，CFPREV）的启动指令滞后于故障层，进而导致非故障层换流器发生换相失败。在此基础上，文献［17］提出了高低端换流器的协调控制策略，并基于滑窗傅里叶变换谐波电压检测提出CFPREV 算法，但未考虑高次谐波分量的影响。文献［18］将换相电流时间积分面积指标与原有CFPREV 结合，提高了非故障层对故障的灵敏度；文献［19］在此基础上提出了定关断面积控制策略，进一步提高预防效果。但以上研究均未充分考虑直流侧电流的瞬时变换特征，导致故障较严重时无法有效抑制非故障层的换相失败。因此特高压直流分层接入系统高低端换流器同时发生换相失败的问题仍需进一步研究。

针对上述问题，本文提出了一种考虑直流电流瞬时微分的特高压直流分层接入系统非故障层CFPREV 策略。该策略根据换相失败过程中直流电流的变化特征，实时计算直流电流的预测值，将电流预测值与换相电流时间积分面积指标相结合，代替原有CFPREV 模块，减小了各层换流器的触发角；同时依据电流预测值和等效直流输入电阻动态调整VDCOL 的输入指令，提高了各层VDCOL 的响应速度，增大了其输出的直流电流指令值。最后基于仿真平台PSCAD／EMTDC 搭建了特高压直流分层接入系统模型，验证所提控制策略的有效性。

1 特高压直流分层接入系统介绍

1.1 分层接入系统结构

特高压直流输电系统包括单层接入和分层接入结构，单层接入系统中4 台12 脉动换流器并联接入同一条交流母线，因此当交流系统发生故障后，可认为换流器距故障点的电气距离相同，如附录A 图A1（a）所示；分层接入系统中4台12脉动换流器并联接入不同电压等级的交流系统，离接地点较近的低端换流器接入1 000 kV 交流系统，离接地点较远的高端换流器接入500 kV 交流系统，如附录A 图A1（b）所示。双层系统通过阻抗相连，因此分层接入系统可能出现本地换相失败和并发换相失败。

1.2 分层接入系统换相失败特性

换相失败是指换流器的2 个阀在换相过程中，因换相过程未进行完毕或原定关断的阀在承受反压期间重新导通的情况。一般情况下，当系统关断角γ＜10° 时认定逆变器发生换相失败。高、低端逆变器关断角分别为：

式中：γ为逆变器关断角；Xc为换流阀等效换相电抗；Id为流经换流阀的直流电流；U为换流母线电压有效值；k为换流变压器变比；β为换流阀超前触发角；下标H、L分别表示高、低端换流阀，后同。

特高压直流分层接入系统的受端交流系统等值结构如图1所示。图中：Z2、Z3分别为逆变侧500 kV、1 000 kV 系统等值阻抗；Z23为逆变侧分层接入系统间的等值联系阻抗。由于受端系统通过阻抗相连，其中一层发生故障可能引发非故障层换流器的电气量随之变化，进而导致高、低端换流器同时发生换相失败。

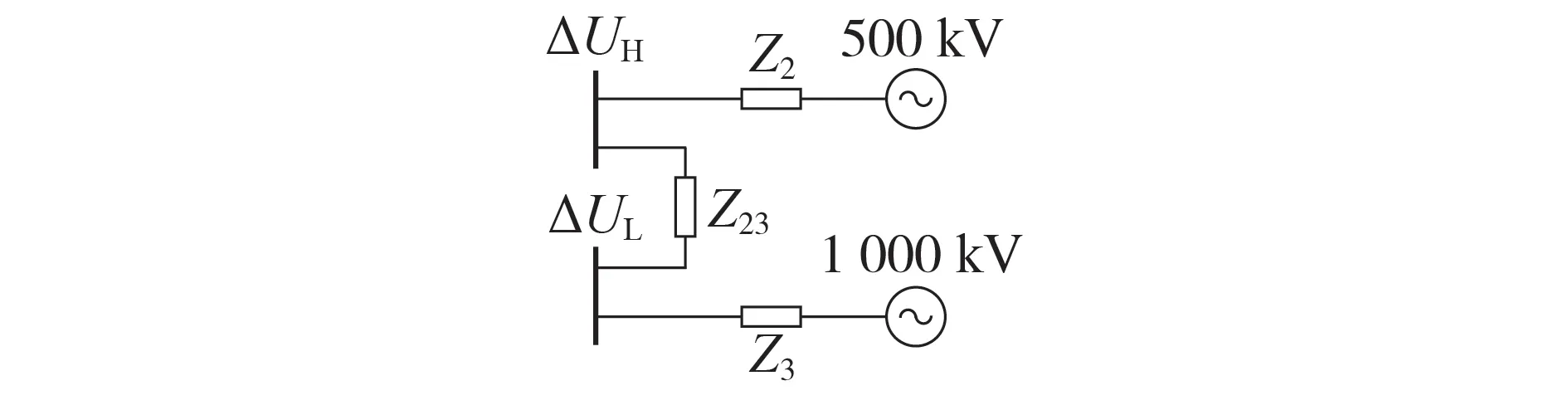
图1 特高压直流分层接入系统的受端交流系统等值结构Fig.1 Equivalent structure of receiving-end AC system of UHVDC hierarchical connection system

假设500 kV 交流系统发生故障后，对应交流母线线电压跌落值为ΔUH，1 000 kV交流母线线电压跌落值为ΔUL，二者存在如下关系：

在其中一层所连交流系统发生故障后，由于该层换流阀距故障点电气距离较近，故障层换流母线电压快速跌落、直流电流增大，发生换相失败。由于非故障层换流阀距故障点电气距离较远，换流母线电压跌落程度较低，但高、低端换流阀在直流侧串联，直流电流激增。由于信号传输需要时间，在非故障层换流母线电压跌落导致CFPREV 触发之前，直流电流的大幅上升就已经引发非故障层的换相失败，因此非故障层发生换相失败的主要原因是迅速增加的直流电流。

2 分层接入系统故障期间直流电流近似解析计算

2.1 稳态期间直流电流计算方法

分层接入系统每极由N组6 脉动换流器串联组成，逆变侧每组又分为高端换流器和低端换流器。稳态运行时，换流阀理想空载直流电压为：

式中：Udo为理想空载直流电压；下标r、i 分别表示整流侧、逆变侧，后同。

整流器和逆变器直流出口端对地电压分别为：

式中：αr为整流侧触发角；R为换流器等效换相电阻。

分层接入系统中，逆变侧高、低端换流阀各参数遵循式（6）所示的关系。

因此稳态运行时流经换流阀的直流电流Id为：

式中：Rd为直流线路等效电阻。由上述分析可得稳态时直流等效电路，如附录A图A2所示。

2.2 故障期间直流电流近似解析计算

假设逆变侧500 kV 交流系统发生故障后，考虑直流线路上电感、电容以及平波电抗器对电流变化的影响，可得出故障后暂态直流电路，如附录A 图A3（a）所示。为简化计算，将故障后逆变侧直流电流Idi(t)近似分解为整流侧直流电流Idr(t)和电容电流IC(t)［20］。附录A 图A3（b）、（c）为分解后各电流分量的计算电路。

由于故障后到换相失败发生前的时间很短，故近似认为整流侧交流母线电压和触发角不变；由于整流侧直流电流近似计算电路为一阶电路，故应用一阶电路三要素法，即可得到故障时刻为t0时整流侧的直流电流，如式（8）—（11）所示。

式中：Idr∞为故障后整流侧直流电流稳态值；Idr0为故障前整流侧直流电流；τ为时间常数；Req为等效换相电阻与直流线路电阻之和；Leq为平波电抗器电感与直流线路电感之和；KΔUH为非故障层故障换流母线电压跌落值，0＜K＜1。

将图A3（c）所示的电容电流计算电路进行拉普拉斯变换，可得到附录A 图A4 所示的s域电路［21］。电容完全放电进入稳态后其两端电压Ui'为：

由于故障前的电容电流IC0-为0，故图A4 中的电容电流IC(s)为：

式中：C为直流线路等效电容；UC0-为故障前等效直流电容两端电压。将式（13）进行拉普拉斯反变换后，可得故障后的电容电流IC(t)为：

则故障期间逆变侧直流电流Idi(t)为：

3 基于直流电流瞬时微分的CFPREV策略

3.1 直流电流预测方法

考虑故障期间逆变侧直流电流计算过于复杂，在故障时刻t0处利用泰勒公式并忽略二阶以上的微分项和余项，得直流电流近似展开式为［22⁃23］：

式中：Δt=t-t0为电流预测时间。在Δt内的直流电流变化量ΔIdi为：

由于一阶微分项和二阶微分项的预测作用和噪声影响不同，综合考虑二者在预测效果的作用和特点，将一阶微分项预测时间Δt1和二阶微分项预测时间Δt2取不同值［14］。修正后的直流电流预测量为：

由于考虑直流电流预测值后直流电压值降低，引入等效直流输入电阻R*，将R*与直流电流预测量ΔId'i相乘后可近似表征电流预测时间Δt内直流电压变化量ΔUd'i，如式（19）所示。

等效直流输入电阻R*的取值由稳态时逆变侧直流出口端电压Udi与直流电流Idi的比值决定，如式（20）所示。

则在电流预测时间后等效直流输入电阻Reqf为：

3.2 预测型换相电流面积控制

换相电流面积是指在换相时间内直流电流曲线与横轴围成的面积。以换流器阀5向阀1换相为例，换相过程如图2所示。图中：Sμ为换相电流面积；μ为换流器换相角；eb、ec分别为阀5和阀1的相电压；I5和I1分别为流入阀5 和阀1 的直流电流；α为换流器触发角；γmin为换流器最小关断角；ω为旋转角速度。

图2 换流器换相过程Fig.2 Commutation process of converters

由于换相时间极短，对应的换相角μ很小，故可近似认为换相电流在换相时间内呈线性变化，则换相电流面积的表达式可表示为直角三角形面积［24］，如式（22）所示。

联立式（4）—（6）、（22），并考虑电流预测后关断角减小，关断角取临界关断角γ0，得到预测型换相电流面积控制的表达式为：

由式（21）和式（23）可知，预测型换相电流积分面积指标仅与逆变侧直流出口端对地电压Udi、直流电流Idi(t)和电流预测值ΔId'i有关。当系统运行时，Udi和Idi(t)均可实时监测，ΔId'i可通过式（18）计算得到，其余量均为常数，由式（23）可计算出电流预测时间Δt后的换相电流面积。

当交流系统发生故障后，直流电流Idi增大，换相电感上积聚的能量也会增大，导致换相过程中用于能量交换时间延长，最终导致换相角μ的增大。当换相角增大到保证换相过程顺利完成的最大换相角μmax时，此时的换相电流面积即为临界换相电流面积Sμmax。因此可将S'μ与Sμmax的商Ks作为换相电流面积的启动判据。将Ks分别输入最大值保持函数fH和启动判定模块，最大值保持函数fH输出的信号与增益Ggain相乘，以适应换流器的触发角，Ggain取0.075。启动判据模块判定该控制环节是否启动：若Ks大于启动阈值Kt，则换相电流面积控制输出触发角提前量Δαr；若Ks小于等于启动阈值Kt，则重新计算换相电流面积。启动阈值Kt的选取要以输出合适的触发角提前量Δαr为原则：当Kt选取过小时，导致换相电流面积控制的灵敏度过高，影响换流器的正常运行；当Kt选取过大时，换相电流面积控制的灵敏度不足，无法有效抑制换相失败。对于本文所建立的仿真模型，经大量仿真验证后得到效果较好的Kt为0.7。

3.3 基于电流预测的VDCOL

考虑直流电流预测后，输入VDCOL 的直流电压值可由原始电压值减去预测时间Δt内的电压变化值所取代，如式（26）所示。

图3 考虑电流预测后的VDCOL参数变化Fig.3 Variation of VDCOL parameters considering current prediction

在交流系统发生故障后，直流电压降低，直流电流激增，直流电流变化量ΔId'i＞ 0，引入电流预测后可进一步增大直流电压变化值，提前触发VDCOL 指令，且直流电压变化量与故障严重程度有关，可根据故障严重程度动态调整输出的直流电流指令值，从而有效抑制高、低端换流器同时发生换相失败。

3.4 电流预测环节的启动判据

电流预测环节主要依据故障发生后直流电流的变化过程，在直流电流的恢复阶段，可能出现预测后直流电流值小于实际值，提前退出控制环节。故在CFPREV 启动判据的基础上增加直流电流微分的CFPREV策略判据［14］，如式（27）所示。

式中：αiN为逆变器的额定触发角；IdN为直流线路额定电流。

由于系统稳定运行时的各电气量与额定值偏差不大，利用式（22）可提前计算出高、低端换流器的换相失败临界电流变化量，提高预测的速动性，由于稳态时电气量波动不大，因此该预测判据不影响系统的稳态运行。综上所述，基于电流预测的CFPREV结构如附录A图A5所示。

4 仿真验证

4.1 预测时间的选取分析

在一次换相失败的过程中，换相重叠角对应的时间约为2 ms，同一组桥臂导通的时间约为20 ms［14］，因此对于预测时间的选取应在毫秒级至十毫秒级。Δt1为电流预测环节的主导参数，直接关系预测结果，其值越大，直流电流变化量ΔId'的计算结果越大，同一工况下可以提供更大的关断角裕度和触发角提前量以抑制换相失败，且Δt1作用于一阶微分项，因微分带来的噪声较小，故Δt1应取十毫秒级。Δt2为电流预测环节的次要参数，主要根据一阶微分项的变化量对预测结果进行修正，提高预测准确度。但微分环节可以放大噪声，尤其是Δt2作用在二阶微分项，带来的噪声影响大于一阶微分项，因此为了降低噪声对控制效果的影响，Δt2应取毫秒级。

分别在受端500、1 000 kV 侧交流母线设置一系列不同的接地故障，验证预测时间对非故障层换相失败抑制效果的影响。对非故障层换相失败抑制效果见附录A 图A6、A7。由图可知，加入一、二阶预测项后，只要预测时间设置合适，即可有效抑制非故障层的换相失败。在本文搭建的仿真模型中，当Δt1=7.5 ms且Δt2=2 ms时有相对较好的抑制效果。

4.2 系统运行特性对比

为了进一步验证本文所提基于电流预测的CFPREV 策略的有效性，在PSCAD／EMTDC 中搭建图1 所示的特高压直流分层接入系统的仿真模型，模型具体参数如附录A表A1所示。设置3种控制策略如下：①策略1，采用分层接入系统原有控制策略；②策略2，采用文献［18］所提控制策略；③策略3，采用本文所提控制策略。分别在以下2 种工况中进行对比分析。

工况1：在逆变侧500 kV 换流母线处设置三相接地故障，接地电感为0.2 H，故障发生时刻为1 s，持续时间为0.1 s，对以上3 种控制策略进行仿真分析。主要电气量的变化情况如图4 所示。图中：γf、γnf分别为故障层和非故障层关断角；Unf为非故障层换流母线电压；Unf、Id、Pd均为标幺值，后同。

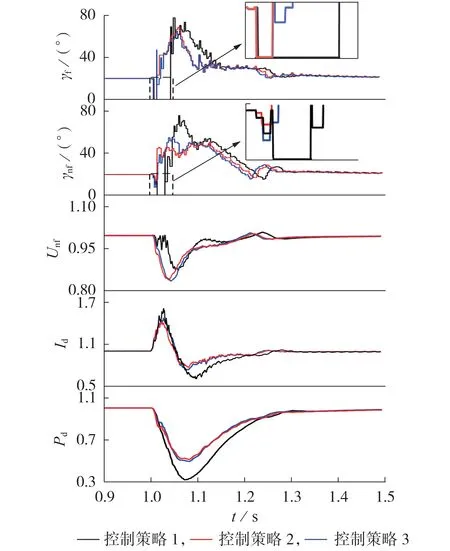
图4 500 kV换流母线三相接地故障下运行特性Fig.4 Operation characteristics of 500 kV converter bus under three-phase grounding fault

由图4 可知，当交流系统发生对称故障后，采用控制策略1 — 3 时，故障层换流器均会发生换相失败，但采用控制策略2、3 时故障层换流器发生换相失败的持续时间更短。当采用控制策略1 时：非故障层换流器发生了换相失败且关断角的恢复时间最长；直流电流的峰值和波动范围在三者中最大，峰值约为1.610 p.u.，峰谷差约为0.992 p.u.；直流功率的跌落程度最大，最小值约为0.336 p.u.；但非故障层换流母线电压的跌落程度相对较小。采用控制策略2 时：非故障层换流器也发生了换相失败，但持续时间较短，关断角最小值约为7.05°；直流电流的峰值约为1.423 p.u.；直流功率跌落的最小值在三者中居中，约为0.511 p.u.；由于该策略基于提前触发思想，故交流母线处的无功需求增大，非故障层交流母线电压的跌落值最大。当采用控制策略3 时：有效抑制了非故障层的换相失败，关断角最小值约为12.30°，具有足够裕度；直流电流的峰值最小，直流功率的跌落值最大，非故障层换流母线的跌落程度相较于策略2也有提升。因此，采用控制策略3可有效提高非故障层抵御换相失败的能力。

工况2：在逆变侧1 000 kV 换流母线处设置单相接地故障，接地电感为0.25 H，故障发生时刻为1 s，持续时间为0.1 s，对以上3 种控制策略进行仿真分析，主要电气量的变化情况如图5所示。

图5 1 000 kV换流母线单相接地故障下运行特性Fig.5 Operation characteristics of 1 000 kV converter bus under single-phase grounding fault

由图5 可知，当逆变侧交流系统发生不对称故障时，采用3 种控制策略均会在故障层发生换相失败。采用控制策略1时，非故障层换流器发生了2次换相失败，直流电流的峰值和直流功率的跌落程度最大。采用控制策略2时，非故障层换流器发生1次换相失败，持续时间略有减少。采用控制策略3 时，非故障层换流器未发生换相失败，关断角最小值约为13.702°；各电气量的变化幅度更小，提高了故障后系统的运行特性。

4.3 换相失败免疫能力指标对比

为更加全面地验证本文所提控制策略的有效性，采用换相失败免疫指标（commutation failure im⁃munity index，CFII）量化3种控制策略下特高压直流分层接入系统对故障的免疫能力，CFII 值越大说明换流器对换相失败的免疫能力越强，计算公式为［17］：

式中：λCFII为CFII 值；UN为逆变侧换流母线额定线电压；Lm为临界故障电感；PdN为直流系统的额定功率。

分别在逆变侧500、1 000 kV 换流母线处设置单相接地和三相接地故障，故障时刻分别为1、1.005 s，持续时间为0.1 s，计算3 种控制策略在非故障层换流器的CFII 值，结果分别见附录A 表A2、A3。由表可知，无论故障时刻是1 s 还是1.005 s，控制策略2和控制策略3 的非故障层换流器CFII值相较于控制策略1均有显著提升，且采用控制策略3时的CFII值大于控制策略2。由此可知，本文提出的基于电流预测分层接入系统换相失败抑制策略能有效提高非故障层换流器对换相失败的抵御能力。

4.4 通信延迟对抑制策略效果影响

对于引入电流预测后的CFPREV 策略而言，微分项的计算和信号传输需要一定时间，为了全方位验证所提控制策略的有效性，在所提控制策略中增加通信延迟环节，采用CFII 值量化通信延迟对所提控制策略的影响。

分别在逆变侧500 kV换流母线处设置单相接地和三相接地故障，以0.5 ms为步长，分别设置0～3 ms的通信延迟，非故障层换流器CFII 值见附录A 图A8。由图可知：随着通信延迟的增大，非故障层换流器的CFII 值减小，说明本文所提控制策略在一定程度上受通信延迟的影响，且影响程度随延迟时间的增加逐步加深。但即便通信延迟为3 ms，当逆变侧500 kV 换流母线发生单相和三相接地故障时，非故障层换流器的CFII 值分别为1.681 和0.900，均大于相同故障下控制策略2 的CFII 值，说明在考虑电流预测计算环节和信号传输环节所需时间的情况下，本文所提控制策略对非故障层换流器换相失败的抑制效果亦有优越性。

5 结论

本文在分析特高压直流分层接入系统换相失败特征的基础上，提出一种基于电流预测的分层接入系统CFPREV策略，在理论分析和仿真验证后可得：

1）所提基于电流预测的分层接入系统CFPREV策略可提前触发VDCOL 指令，增加非故障层的触发角提前量，降低非故障层换相失败的发生概率；

2）合适的预测时间可有效降低非故障层发生换相失败的风险，但预测时间设置过大会带来噪声影响，恶化系统的运行环境；

3）无论高、低端换流母线发生单相或三相接地故障，所提控制策略均能有效提升CFII 值，降低高、低端逆变器同时发生换相失败的概率；

4）针对微分环节带来的噪声影响，在实际工程中可增加鲁棒回归平滑降噪、小波联合降噪等技术来降低误差，且后续研究可通过粒子群优化等启发式算法对本文的预测时间常数进行更精确的求解。

附录见本刊网络版（http：//www.epae.cn）。