基于自适应时序表征和多级注意力的超短期风电功率预测

张 越，臧海祥，程礼临，刘璟璇，卫志农，孙国强

（河海大学 能源与电气学院，江苏 南京 211100）

0 引言

风力发电被认为是推进能源转型和可持续发展的重要方式之一［1］，然而受气象因素影响，风电功率具有较强的波动性和随机性，这给电力系统的功率平衡、规划调度带来了较大的挑战。对超短期风电功率进行准确的点预测和区间预测，能够确保电力系统的经济调度和安全运行。

传统的风电功率预测方法包括物理方法和统计方法［2］。近年来，以机器学习和深度学习为主体的人工智能方法已被广泛应用于风电功率预测［3］。支持向量回归［4］、随机森林［5］等机器学习方法应用于小样本数据集能取得良好的预测精度，然而随着风电相关数据的大规模增加，机器学习方法难以挖掘其中的复杂非线性关系，在很多预测场景中性能明显下降。相较而言，深度学习方法能从海量数据中学习到关键特征［6］，提高预测表现。以卷积神经网络（convolutional neural network，CNN）、长短期记忆（long short-term memory，LSTM）网络为基础的深度学习模型在风电功率预测中表现出优异的性能。文献［7］利用CNN 提升了模型对风电功率数据的特征提取能力；文献［8］利用改进的LSTM 网络进行风电功率预测；文献［9］基于双向长短期记忆（bi-direc⁃tional long short-term memory，Bi-LSTM）网络，提出了一种深度级联残差模型，获得了可靠的点预测、区间预测结果。

随着研究的不断深入，在深度学习模型中引入注意力机制，往往能够进一步提升模型的预测表现。文献［10］在LSTM 网络的基础上引入特征空间和时序双重注意力机制；文献［11］构建了基于注意力机制的时序卷积网络（temporal convolutional network，TCN）用于风电功率的超短期点预测和区间预测；文献［12］引入自注意力机制改进了TCN 结构；文献［13］结合一维卷积神经网络（one-dimensional CNN，1D-CNN）、堆叠Bi-LSTM 网络和注意力机制，实现了高精度的风电功率预测。

高效的数据处理方法也常与深度学习模型相结合用于风电功率预测，如变分模态分解方法［14］、奇异谱分解方法［15］、改进的自适应噪声完备集合经验模态分解方法［16］。这些方法通过分解风电功率序列，获取时间的相关特征，从而提升预测精度。然而，上述处理方法需要人为提取风电功率序列中的时间信息，其过程往往与模型实际的预测环节相分离，这会增加模型性能对数据处理的依赖性。为了进一步提升模型的预测表现，现有方法通常将历史气象特征也作为模型的输入，然而不同时刻的气象特征对风电功率的实际影响是不同的，直接将历史气象特征作为模型的输入，容易忽略其与风电功率之间的动态耦合关系，导致模型的预测性能下降。针对上述研究的不足，本文提出了一种基于自适应时序表征和多级注意力的超短期风电功率预测方法，主要创新点如下：

1）采用时序嵌入层Time2Vec 对风电功率序列进行表征，将时间序列预处理过程集成到深度学习模型中，有效提取了风电功率的多尺度时间信息，提升了时间序列处理的自适应性；

2）引入多级注意力提升模型的预测表现，包括利用自注意力充分捕捉风电功率序列的自相关性，利用交叉注意力深度挖掘风电功率与气象因素之间的耦合关系，利用全局注意力有效过滤LSTM 网络隐藏层单元状态中的噪声；

3）构建了兼顾多维特征序列内在时空依赖关系的时序特征提取模块，即时空卷积神经网络-长短期记忆（spatiotemporal convolutional neural networklong short-term memory，STCNN-LSTM）网络，在充分考虑多维特征序列时间相关性和空间相关性的基础上，提取了更高层次的时序特征。

1 本文方法的基本原理

本文结合自适应时序表征方法Time2Vec、自注意力、交叉注意力、1D-CNN、LSTM 网络和全局注意力建立了超短期风电功率预测模型，该模型以历史风电功率序列和影响风功率变化的多元气象序列作为输入，进行超短期风电功率的点预测和区间预测。所建模型的基本结构如图1 所示。图中：Q、K、V分别为查询矩阵、键矩阵、值矩阵。

针对风电功率波动性、突变性显著的特点，首先利用Time2Vec 得到原始风电功率序列的时序表征向量，将其与原始序列拼接后，输入全连接层中，得到能够反映其多尺度时间特性的高维风电功率序列。

其次，考虑不同时间步风电功率值之间的影响，利用位置编码和多头自注意力重构所得高维风电功率序列，充分捕捉其自相关性。

然后，考虑风电功率与气象因素之间的耦合关系，利用交叉注意力重构风电功率序列与多元气象序列，得到包含两者耦合关系的多维特征序列。为了避免原始风电功率数据信息的丢失，本文在利用多头自注意力、交叉注意力对风电功率的相关数据进行重构时均引入了残差连接，以保留风电功率的原始特征信息。

在此基础上，利用1D-CNN 沿时间和特征方向分别获取多维特征序列的时间相关性和空间相关性，进而利用LSTM 网络充分提取两者的时序特征，将所得时序特征经全局注意力去噪和门控机制融合后，输入全连接层，分别进行点预测和区间预测。

2 风电功率相关数据重构

2.1 基于Time2Vec的风电功率序列表征

作为一种新型时间序列表征方法，Time2Vec 能够嵌入不同的深度学习模型中［17］。对于给定的时间标量τ，经Time2Vec 处理后可得到其高阶特征表示tt2v(τ)，具体可表示为：

式中：tt2v(τ)[i]为tt2v(τ)的第i个分量，i=0 时为线性分量，1≤i≤k时为周期性分量，k为周期性分量的数量；ωi、φi分别为第i个周期性分量对应正弦函数的角频率、相位，均为可更新的参数，sin(ωiτ+φi)用于捕捉时间的周期性模式；ω0、φ0分别为线性分量的角频率、相位，用于捕获时间的非周期性模式。

本文利用Time2Vec 对原始风电功率序列进行表征，示意图见附录A图A1，具体过程可表示为：

式中：Y∈RT为给定时间窗口长度T内的风电功率序列；Yconcat∈RT×(k+2)为Time2Vec分量Time2vec(Y)与原始风电功率序列拼接所得结果；Cconca（t·，·）为拼接函数。

2.2 基于多头自注意力的风电功率序列重构

自注意力机制［18］通过构建序列不同位置元素之间的联系和影响，得到原始序列新的表现形式。给定一个输入序列Z∈Rl×d，其中l为序列长度，d为变量维数。在自注意力机制中，该输入序列首先被转变为查询矩阵Q、键矩阵K、值矩阵V，如式（3）所示。

式中：WQ∈Rd×dk、WK∈Rd×dk、WV∈Rd×dv为参数矩阵，dk、dv为变换维度；Q∈Rl×dk、K∈Rl×dk、V∈Rl×dv分别为基于原始输入序列得到的查询矩阵、键矩阵、值矩阵。基于上述变量可计算得到自注意力机制的输出A为：

式中：Softmax（·）为归一化指数激活函数。

多头自注意力机制是在自注意力机制的基础上发展形成的，其计算方式与自注意力机制相同，区别在于多头自注意力基于输入序列进行多个自注意力的并行计算。多头自注意力机制的计算过程可表示为：

式中：A(1)、A(2)、…、A(m)为各头自注意力的计算结果；O为多头自注意力机制的输出；m为多头自注意力机制的“头数”；WO为参数矩阵。

多头注意力机制的结构示意图见附录A 图A2，本文利用其充分捕捉功率数据的自相关性，进而对风电功率序列进行重构，具体步骤如下。

首先，在2.1 节的基础上，将Yconcat映射至d维空间，得到Yenc∈RT×d；由于多头自注意力在计算时并没有考虑数据的位置信息，因此采用位置编码将位置信息添加到序列中，保留风电功率序列的时序特性用于后续的建模。位置编码的计算方式为：

式中：ppos为序列索引；i为维度索引；Eppos，2i、Eppos，2i+1为位置编码的计算结果。将上述映射到d维空间的序列与位置编码结果相加，即可得到带有位置信息的高维风电功率序列Ynew∈RT×d。

然后，按照式（3）—（5）对高维风电功率序列进行重构，具体过程如下：

式中：WQy、WKy、WVy、WOy为参数矩阵；Qy、Ky、Vy分别为基于高维风电功率序列Ynew所得查询矩阵、键矩阵、值矩阵；Ay为自注意力机制的输出；A、A、…、A为各头自注意力的计算结果；Oy∈RT×dy为经多头自注意力重构后的新型风电功率序列，dy为新型风电功率序列的维度。

2.3 基于交叉注意力的风电功率与气象因素重构

风速、温度、湿度等气象参数是影响风电功率的重要因素，因此需要考虑风电功率与多元气象变量之间的联系。本文利用交叉注意力重构风电功率序列和多元气象序列，以更好地捕捉气象因素对风电功率的动态影响。利用交叉注意力对两者进行重构时，基于2.2节所得新型风电功率序列变换得到查询矩阵，基于原始多元气象序列变换得到键矩阵和查询矩阵，具体过程如下：

式中：X∈RT×n为影响风电功率变化的多元气象序列，n为气象变量的数量；WQxy、WKxy、WVxy、WOxy为参数矩阵；Qxy、Kxy、Vxy分别为相应的查询矩阵、键矩阵、值矩阵；Axy为交叉注意力机制的输出；、A、…、为各头交叉注意力的计算结果；Oxy∈RT×dxy为最终得到的多维特征序列（dxy为该序列的维度），该序列充分考虑了风电功率与气象因素之间的耦合关系，是对风电功率和气象因素进行有效重构后的高级特征表示。

3 超短期风电功率预测模型

3.1 基于STCNN-LSTM网络的时序特征提取

当1D-CNN 和LSTM 网络应用于时间序列预测时，能够有效捕获时间序列的高级特征和重要信息［19］。本文充分利用1D-CNN和LSTM网络在时序建模中的优势，构建了STCNN-LSTM 网络，以提取2.3节中Oxy∈RT×dxy的时序特征，具体过程如图2所示。

图2 STCNN-LSTM网络时序特征提取过程Fig.2 Temporal feature extraction process of STCNN-LSTM network

首先，利用1D-CNN 构建时间卷积模块和空间卷积模块，对Oxy进行初步特征提取。时间卷积模块使用卷积核数量为dxy的1D-CNN 沿时间维度对Oxy进行卷积运算，所采取的填充方式为“causal”，具体计算方式为：

式中：Wtem、btem分别为卷积运算的权重、偏置；Relu（·）为激活函数；ltem∈RT×dxy为输出结果；“*”为卷积运算。时间卷积模块可以有效地学习多维特征序列在时间维度上的依赖关系，然而其在捕获多元序列空间依赖关系方面的能力有所欠缺，空间卷积模块则是针对这一不足而设计的。空间卷积模块使用卷积核数量为T的1D-CNN 沿特征维度对Oxy进行卷积运算，所采取的填充方式为“same”，具体计算方式为：

式中：Wspa、bspa分别为卷积运算的权重、偏置；lspa为空间卷积模块的输出，其充分学习了多维特征序列之间的空间依赖关系。

基于上述时间卷积模块和空间卷积模块所得结果，利用LSTM 网络进一步提取其时序特征，具体可表示为：

式中：LSTM( ⋅ )表示LSTM 网络；Htem∈RT×U为基于ltem的网络输出，U为LSTM网络的隐藏层单元数量；Hspa∈RT×U为基于lspa的网络输出；h∈RU、h∈RU（t=1，2，…，T）为在时间步t对应隐藏层单元的状态。

为了提升模型的预测表现，本文引入注意力机制进一步变换所得时序特征。现有研究针对LSTM网络输出建立的注意力机制往往为不同时间步对应的隐藏层状态向量分配一个注意力权重系数［10，13］，这种方式不能过滤掉每个时间步隐藏层状态中的噪声［20］。因此，本文设计了一种全局注意力，兼顾了时间步和隐藏层单元状态2个角度，为LSTM 网络的输出分配一个注意力权重矩阵，具体的变换过程如下：

式中：E∈RT×U；co∈RU为最终的输出；V͂、W͂为参数矩阵；tanh( ⋅ ) 为 激 活 函 数；et，u（t=1，2，…，T；u=1，2，…，U）为变换所得矩阵E的元素；βt，u为全局注意力权重矩阵的元素；“⊙”为哈达玛积；ht为在时间步t隐藏层单元的状态。

利用全局注意力对所得Htem、Hspa进行变换，可得co，tem∈RU、co，spa∈RU，进而引入门控机制，融合所得时序特征，可得时序特征融合结果o为：

式中：μ为门控系数，其取值范围为［0，1］。

3.2 基于多级注意力和STCNN-LSTM网络的超短期风电功率点预测

基于多级注意力和STCNN-LSTM（multi-level attention STCNN-LSTM，MASTCNN-LSTM）网络的超短期风电功率点预测的流程图如附录A 图A3所示。其中：数据预处理阶段对异常值和缺失值进行清洗，并在此基础上划分训练集和测试集；风电功率相关数据重构阶段充分挖掘了风电功率的多尺度特性、气象因素对风电功率的动态影响，并形成了包含两者耦合关系的多维特征序列；STCNN-LSTM 网络实现了对上述多维特征序列深层时序特征的有效提取，进而将其输入全连接层中，得到最终的风电功率点预测值。模型训练时采用均方误差（mean squared error，MSE）作为损失函数，其表达式为：

式中：γMSE为MSE 值；yi为第i个样本的实测值；ŷi为第i个样本的预测值；Ns为训练集样本总数。在训练过程中不断更新模型参数，使得MSE 尽可能小；当训练达到设定次数后，可基于测试集验证模型的实际预测效果。该模型的点预测过程可描述为：

式中：f（p·）为MASTCNN-LSTM 网络的非线性映射函数+λ为预测步长为λ时的风电功率预测值。

本文选取均方根误差（root mean squared error，RMSE）、平均绝对误差（mean absolute error，MAE）、相关系数（correlation coefficient，CORR）、决定系数（coefficient of determination，CoD）作为点预测的评价指标，其计算公式分别为：

式中：eRMSE、eMAE、cCORR、cCoD分别为RMSE、MAE、CORR、CoD 值；ya、ŷa分别为测试集样本的实际均值、预测均值；N为测试集样本总数。评价模型时，所得RMSE、MAE 值越小，CORR、CoD 值越大，则模型的点预测精度越高，预测效果越好。

3.3 基于分位数回归和MASTCNN-LSTM 网络的超短期风电功率区间预测

风电功率区间预测通过预测实际功率值的上下界，得到给定置信度下的预测区间［21］。本节在3.2节中点预测模型的基础上引入分位数回归（quantile regression，QR），构建基于QR 和MASTCNN-LSTM（QR-MASTCNN-LSTM）网络的深度神经网络进行超短期风电功率区间预测。QR 被用于研究自变量与因变量条件分位数之间的关系，并得到因变量的条件概率分布。在QR 神经网络中，QR 用于揭示历史输入对风电功率条件分布的影响规律，从而得到不同分位数水平下的风电功率预测值。

基于QR-MASTCNN-LSTM 网络的超短期风电功率区间预测流程图如附录A 图A4所示，其同样包括数据预处理、风电数据重构、STCNN-LSTM 网络时序特征提取等过程。点预测模型在训练时使用MSE作为目标损失函数，不能得到不同条件分位数对应的风电功率值，因此所提区间预测模型在模型训练阶段选取分位数损失（quantile loss，QL）作为目标损失函数，其数学表达式为：

式中：γQL为QL 值；qj为第j个分位数；为在分位数水平qj下进行预测的第i个样本预测值；Q为分位数的数量。训练阶段同样是在设定的训练周期内不断更新模型参数，以获得尽可能小的QL。

在进行区间预测时，对于显著性水平为α的情形，实际风电功率值落在预测区间内的理论概率被称为预测区间名义置信度（prediction interval nomi⁃nal confidence，PINC），其表达式为：

式中：cPINC为PINC。

此时，对于第i个样本的实测值，其所形成的预测区间为：

式中：fi( ⋅ )为QR-MASTCNN-LSTM 的非线性映射函数；U、L分别为显著性水平α下预测步长为λ时预测区间的上、下界。

在模型评价阶段，选用平均覆盖误差（average coverage error，ACE）、预测区间归一化平均宽度（prediction interval normalized average width，PINAW）、温克勒得分（Winkler score，WS）作为区间预测的评价指标，其计算公式分别为：

式中：eACE、wPINAW、sWS分别为ACE、PINAW、WS；Ui、Li分别为第i个样本预测区间的上、下界；hi为判断第i个样本的实测值是否落在预测区间内的状态变量，若落在预测区间内，则hi=1，否则hi=0；θi=Ui-Li；max {y}、min {y}分别为实测值的最大值、最小值。当评价模型时，ACE 值在0 附近表示预测区间的覆盖可靠性较高，PINAW 用于衡量测量预测区间的宽度，WS 则用于衡量预测区间的锐度，当满足一定的可靠性要求时，PINAW 值越小，WS越接近0，模型的区间预测性能越好。

4 算例分析

4.1 算例概况

本文首先进行点预测和区间预测，分别验证所提方法进行超短期风电功率预测的准确性和可靠性；在此基础上，设置消融实验以分析所提模型中的重要组成部分对模型预测效果的提升作用；为了探究气象因素对模型预测性能的实际影响以及所提方法在极端天气情况下的有效性，还对比分析了考虑与不考虑气象因素时所提模型的预测表现；最后，对所提模型的运行时间进行了讨论，以验证其在超短期风电功率预测中的可行性。

本文所用数据源自江苏某容量为49.5 MW 的风电场，具体为2017年1月1日至2017年12月31日的风电功率、气象数据，气象因素包括风速、风向、温度、气压、湿度；数据采样间隔为15 min，共计采样35 040 个样本，并划分前30 000 个样本作为训练集，后5 040 个样本作为测试集。所用滑动窗口长度为48，即将目标预测时刻之前12 h的风电功率、气象数据作为模型输入；实验中的预测步长为1，即进行提前15 min（超短期范畴）的风电功率预测。

本文所有深度学习模型均基于Tensorflow 这一深度学习框架进行构建，当各模型进行训练时，选取Adam 作为优化器，验证集比例为0.1，批量大小为512，总训练迭代次数为80 次。为了确保实验结果的准确性和客观性，实际算例测试时各模型均运行5次，用所得结果的均值来评估模型的预测表现。

4.2 点预测结果分析

为了充分验证本文所提模型在进行点预测时的有效性，选取6 个模型进行对比分析，分别为TCN、LSTM 网络、Bi-LSTM 网络、双重注意力LSTM（dualstage attention LSTM，DALSTM）网络［10］、自注意力时序卷积网络-LSTM（self-attention temporal convo⁃lutional network-LSTM，SATCN-LSTM）网络［12］以及基于Time2Vec、注意力的卷积Bi-LSTM（Time2Vec attention based convolutional Bi-LSTM，TACBi-LSTM）网络［13］。不同模型的点预测结果如表1所示。

表1 不同模型的点预测结果Table 1 Point forecasting results of different models

由表1知，MASTCNN-LSTM网络的点预测精度最高，其RMSE、MAE 分别为2.233、1.197 MW，CORR、CoD分别为0.972 0、0.944 3。相比于基础的深度学习模型，本文所提模型的预测精度显著提升，RMSE 下降了10.04 %～11.74 %，MAE下降了22.88 %～22.44 %；相比于文献［10，12⁃13］中高效的风电功率预测模型，本文所提模型仍能获得更小的预测误差，其RMSE 下降了3.56 %～7.16 %，MAE 下降了12.02 %～21.68 %，体现了所提模型在进行超短期风电功率点预测方面的优越性。

不同模型的预测误差分布曲线如图3 所示。由图可以看出，本文所提模型在测试集上的预测误差在0 值附近分布最为集中，其分布曲线相比于其他模型的分布曲线也更窄，这表明本文所提模型在测试集上的总体误差更小，预测效果更好。

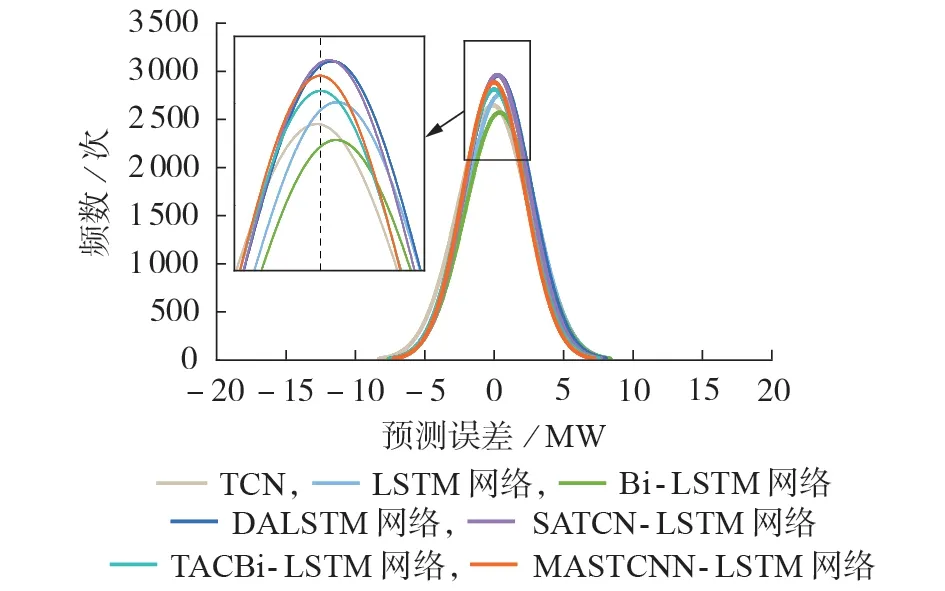
图3 不同模型的预测误差分布曲线Fig.3 Forecasting error distribution curves of different models

不同时段各模型的点预测曲线和实际风电功率曲线的拟合情况见附录B 图B1。由图可以看出，受风速等因素的影响，风电功率具有较强的波动性。对比可知，MASTCNN-LSTM 网络的综合拟合效果最优，具体表现在：对于风电功率波动较大的情形，如图B1（a）和图B1（c）出现的“爬坡”现象，相比于其他模型，本文所提模型的预测值曲线都与实际值曲线更为贴合；对于风电波动较小的情形，如图B1（b）中起始、中间时段以及图B1（c）中最后时段出现的“小幅振荡”现象，本文所提模型的预测值曲线仍与实际值曲线最为接近。

4.3 区间预测结果分析

相比于点预测，区间预测通常能提供更多有助于电力系统风险分析的信息［22］。本文所测试的区间预测模型均基于4.2 节中的点预测模型，利用QL 函数进行训练，构建相应的QR 神经网络。算例测试验证了PINC 为90 %、85 %、80 % 时各模型的区间预测表现，具体结果如附录B 表B1 所示。由表可知：当PINC 为90 %、85 % 时，QR-MASTCNN-LSTM 网络的ACE 绝对值、PINAW、WS 绝对值均最小，这表明本文所提模型生成的预测区间更窄，具有更高的可靠性；当PINC 为80 % 时，QR-MASTCNN-LSTM 网络的ACE 为2.532 1，表明其区间覆盖率高于给定的置信水平，但其PINAW 值最小，且WS值均优于其他模型，这表明该模型提供了可靠的预测区间，且宽度相对较窄。综上可知，本文所提模型在3 种置信水平下生成的预测区间具有较高的可靠性，且基于不同评估指标体现了最高的区间预测精度。

为了更为直观地比较不同模型的区间预测效果，选取QR-SATCN-LSTM 网络、QR-TACBi-LSTM 网络、QR-MASTCNN-LSTM 网络模型在不同时段3 种置信度下产生的预测区间进行可视化分析，可视化结果如附录B 图B2 所示。由图可知，3 种模型所产生的预测区间均能较好地覆盖实际的风电功率值，以表征风电功率预测的不确定性。相比于其他2 种区间预测模型，QR-MASTCNN-LSTM 网络生成的预测区间更为紧凑，其区间包络线也能较好地描述风电功率的波动特征，区间预测效果最好。

4.4 消融实验结果分析

为了验证本文所提方法中重要组件对其预测性能的实际影响，本节针对点预测和区间预测分别进行消融实验，所用实验数据和相应的参数设置均与前文保持一致，所得结果见表2 和附录B 表B2。表中：情形A — D 分别删除了Time2Vec、多头自注意力、交叉注意力、全局注意力组件；情形E 为本文所提点预测方法，集成了上述4个组件。

表2 消融实验的点预测结果Table 2 Point forecasting results of ablation experiment

由表2 可知：相较于情形A，情形E 利用Time-2Vec组件对风电功率序列进行表征学习，其MAE降低了2.38 %；相较于情形B，情形E 的MAE 降低了13.96 %；相较于情形C，情形E 引入交叉注意力组件进一步提高了点预测精度；相较于情形D，情形E 引入全局注意力组件同样提升了模型的点预测表现。

由表B2 可知，情形A 和情形B 在不同的置信度约束下得到的预测区间宽度比情形E更宽，就WS指标而言，情形E 进行区间预测时的综合性能也优于情形A 和情形B，可见Time2Vec、自注意力组件能够充分挖掘风电功率序列自身的多尺度特性，使得预测区间能更好地描述风电功率的波动特征；情形C在90 %、80 % 置信度约束下取得最优的预测区间宽度，相较而言，情形E 在3 种置信度约束下的WS 绝对值都更小，这表明交叉注意力组件能够有效提升区间预测的锐度；情形D在90 %、85 % 置信度约束下取得较好的区间预测效果，但在80 % 置信度约束下的预测效果有所下降，尤其是区间覆盖率下降显著。综上可知，情形E的稳定性更好。

综上所述，本文所提方法中的4 个重要组件在进行实际的超短期风电功率预测时，能够充分发挥自身的效能，不同程度地提升模型进行点预测和区间预测的综合性能。

4.5 气象因素对风电功率预测的影响分析

为了探究进行超短期风电功率预测时考虑气象因素的必要性，本节对比分析了考虑、不考虑气象因素时所提模型的预测效果，对应的点预测和区间预测结果如附录B 表B3 所示。由表可知，考虑气象因素时，模型的点预测和区间预测效果均更好。特别的是，当进行区间预测时，若不考虑气象因素，则模型的区间覆盖率远低于给定的置信水平，这是因为气象因素对风电功率的变化有重要的影响，将其作为输入更有利于模型描述风电功率的不确定性。

极端天气情况下考虑、不考虑气象因素时本文所提模型的风电功率预测表现如图4 所示。受极端天气影响，风电功率呈现剧烈的波动，幅值变化范围较大。对比可知，考虑气象因素时所得点预测曲线的拟合效果更好，所得预测区间同样能够较好地覆盖实际的风电功率值，上述结果再次验证了进行超短期风电功率预测时考虑气象因素的必要性，也说明了所提方法应用于极端天气情况下风电功率预测的可行性。

图4 极端天气情况下本文所提模型的风电功率预测表现Fig.4 Wind power forecasting performance of proposed model under extreme weather condition

风电功率相关数据重构的具体表现如附录B 图B3 所示，该重构过程首先基于输入样本，利用Time2Vec 以向量嵌入的形式提供时间表示。由图B3 可知：自注意力使得模型在实际预测时更关注邻近时刻（第47、48 个时间步）的风电功率；而对于不同时刻的气象特征，其对预测的影响各异，交叉注意力使得模型着重关注特定时刻的气象特征，以动态捕捉不同时刻对应气象因素对风电功率的影响，并形成包含两者耦合关系的多维特征序列。

4.6 不同模型的运行时间对比分析

本文进一步分析了不同模型的运行时间，不同点预测模型的训练用时和测试用时如表3 所示。由表可知，MASTCNN-LSTM 网络、TACBi-LSTM 网络的训练用时和测试用时均更长，这是因为两者的模型结构更深。在增加一定计算成本的基础上，本文所提模型的预测精度提升明显，且其在测试集上的计算时间仅为12.0 s，远小于目标预测步长（15 min），因而本文所提模型在进行实际的超短期风电功率预测时能够快速高效地得到相应的预测结果。

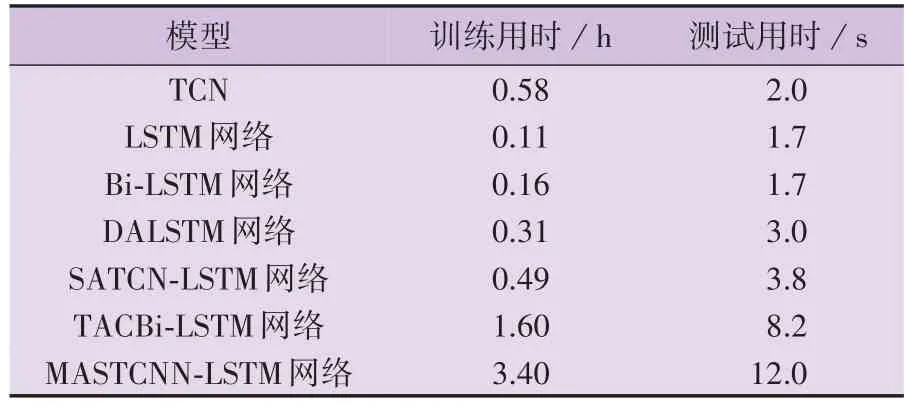
表3 不同点预测模型的运行时间Table 3 Running time of different point forecasting models

5 结论

本文提出了一种基于自适应时序表征和多级注意力的风电功率预测方法，对超短期风电功率进行点预测和区间预测。该方法对风电功率的相关数据进行重构，并利用STCNN-LSTM 网络有效提取了兼顾多元时间序列内在时空相关性的高阶时序特征，同时引入多级注意力机制，提升了模型的预测表现。基于算例测试结果，可得到如下结论：

1）所提模型能够获得准确的点预测结果，进行提前15 min 的风电功率预测时，其测试RMSE、MAE分别为2.233、1.197 MW，CORR和CoD分别为0.972 0、0.944 3，相比于其他深度学习模型，本文所提模型的RMSE、MAE 分别下降了3.56 %～11.74 %、12.02 %～28.44 %，预测精度显著提升；

2）所提模型能够获得可靠的区间预测结果，在置信度为90 %、85 %、80 % 的情形下，其产生的预测区间均具有较高的可靠性，且PINAW、WS 指标均优于其他区间预测模型，能够准确描述预测的不确定性；

3）本文所用的自适应时序表征方法Time2Vec以及基于自注意力、交叉注意力、全局注意力所构建的多级注意力机制，均能够发挥自身的效能，有效提升模型进行点预测和区间预测的性能。

未来，如何构建多源多维数据驱动的深度学习方法来提升风电功率预测的准确性和可靠性，是值得思考和探索的；此外，不同天气状况、不同时间尺度的风电功率预测研究也具有重要的现实意义。

附录见本刊网络版（http：//www.epae.cn）。