Optimal operation of Internet Data Center with PV and energy storage type of UPS clusters

Man Chen,Yuxin Zhao,Yuxuan Li,Peng Peng,Xisheng Tang,3

1.CSG PGC Energy Storage Research Institute,Guangzhou 510000,P.R.China

2.Institute of Electrical Engineering,Chinese Academy of Sciences,Beijing 100190,P.R.China

3.University of Chinese Academy of Sciences,Beijing 100049,P.R.China

Abstract: With the development of green data centers,a large number of Uninterruptible Power Supply (UPS) resources in Internet Data Center (IDC) are becoming idle assets owing to their low utilization rate.The revitalization of these idle UPS resources is an urgent problem that must be addressed.Based on the energy storage type of the UPS (EUPS) and using renewable sources,a solution for IDCs is proposed in this study.Subsequently,an EUPS cluster classification method based on the concept of shared mechanism niche (CSMN) was proposed to effectively solve the EUPS control problem.Accordingly,the classified EUPS aggregation unit was used to determine the optimal operation of the IDC.An IDC cost minimization optimization model was established,and the Quantum Particle Swarm Optimization (QPSO) algorithm was adopted.Finally,the economy and effectiveness of the three-tier optimization framework and model were verified through three case studies.

Keywords: Three-tier optimization framework;Energy storage type of the UPS;EUPS cluster classification method;Quantum Particle Swarm Optimization

0 Introduction

In recent years,the rapid development of big data and artificial intelligence [1] has promoted the large-scale development of Internet Data Center (IDC) [2,3].As the scale of IDCs continues to increase,problems such as high energy consumption,high operating costs,and high carbon emissions have become prominent [4,5].Renewable energy sources have been commonly used to power the IDC loads[6].To promote the consumption of renewable energy,the cost minimization problem of big data analytics on geodistributed data centers connected to renewable energy sources was investigated in [6].The construction of the Zhangbei Cloud Computing Base included a wind-solarstorage integration demonstration project to achieve a low-carbon power supply [7,8].In addition,policies and incentives exist to promote the consumption of renewable energy in IDC [9].This study was conducted in the context of an IDC that includes photovoltaic (PV) clusters.

To ensure safe and reliable power supply,IDCs may have a large number of UPS.Due to the high reliability of power supply,a traditional UPS often has a low utilization rate and gradually becomes an “idle asset”.To improve the utilization rate of the UPS,energy storage type of the UPS(EUPS) with unidirectional and bidirectional regulation was proposed in [10].The difference between the EUPS and traditional UPS is that the EUPS upgrades the grid-side converter and adjusts it to function as an energy-storage battery.The EUPS has the function of “backup power +energy storage”.

To improve the utilization rate of new energy storage,some scholars have studied the operation scheduling of UPSs in IDCs [11].

A UPS charge and discharge control strategy for multiple scenarios was proposed in [11] to reduce dependence of the IDC on the local power grid.Aiming at multi-objective optimization problems,such as low IDC cost and high energy efficiency,a multi-objective optimization algorithm was proposed in [12],and its effectiveness was verified.Considering the costs involved and adopting a UPS to reduce energy consumption and peak energy consumption,a two-stage algorithm was proposed[13] to optimize the electricity costs in the IDC.The energy management system of a data center was studied as a microgrid [14,15].To optimize the operating cost of a data center microgrid,an integrated energy management scheme was proposed in [14].Considering the uncertainties of renewables,wholesale electricity price,and power load,a stochastic resource-planning scheme that minimizes the total cost of the microgrid was proposed in [15].

Certain studies have considered the characteristics of load shifting and UPS operation scheduling in IDCs from the perspective of demand-side response.Different types of load and demand response characteristics have been utilized in [16,17].A two-stage optimized energy management model considering the demand response was investigated in [16].In [17] a bi-level optimal planning framework for Internet data centers and a distribution network considering the demand response was presented.

In [18],considering the complementarities of hydrosolar-wind hybrid renewable energy sources (RESs)and the load demand response,a comprehensive energy consumption model for data center buildings was proposed and solved using a two-stage method to obtain the optimal portfolio.A model in data centers based on P2P transactions and noncooperative game methods was proposed,and the potential of the data center’s demand response was further explored in [19].Considering the workload distribution and considering the number of active servers in the IDCs,an efficient multi-objective approach to demand response was developed in [20].

In summary,energy optimization problems in IDCs are currently being studied largely from two perspectives.First,using the existing UPS system of the IDC for energy storage,which includes the available new energy resources,and by considering the energy composition of the IDC as a microgrid.On the contrary,energy optimization research is conducted from the perspective of demand response and load distribution.

However,it is not sufficient to conduct research on the energy composition of the IDC as a microgrid because to ensure the safety and reliability of the power grid,it is not possible to reverse the power of the IDC to the power grid;therefore,the energy optimization problem of the IDC cannot be simply regarded as an energy optimization problem of the microgrid.Moreover,although existing UPS resources in the data center were used in the current study,the backup-power function of the UPS was not considered when using the UPS resources to participate in the optimal scheduling of the IDC.If a failure occurs during this process,the UPS cannot guarantee power supply to the load.This causes significant economic losses to the IDC.

Therefore,this study summarizes the limitations of existing research and mainly includes the following aspects∶ (1) Not considering the reasonable aggregation of UPS clusters could cause unreasonable scheduling of the UPS when participating in optimal operation of the IDC,resulting in wastage of UPS resources;(2) When a UPS participates in optimal operation of the IDC,few studies considered the backup function and optimal operation of the UPS simultaneously.Although the backup power function of the UPS is top priority,it must be guaranteed;(3) Not considering the backup power function of the UPS power supply and the aggregation management of the UPS cluster in IDC economic dispatching could further lead to unreasonable IDC economic dispatching.

The main contributions of this paper are as follows∶

1) First,considering the IDC—including PV and EUPS clusters—as the research object,a three-tier optimization control framework is proposed.Further,considering the power purchase cost of the IDC,charging and discharging costs,and aging cost of the EUPS cluster,a minimum-cost economic scheduling model is established,and the Quantum Particle Swarm Optimization (QPSO) algorithm is used to implement the model.

2) An EUPS cluster classification method based on the concept of a shared mechanism niche (CSMN) is proposed to form EUPS aggregation units and realize the aggregation and management of EUPS resources.The optimal scheduling model of the EUPS aggregation unit and the dispatchable charge and discharge power model of the EUPS aggregation unit under the backup power function are proposed,which not only ensures the backup power function of the EUPS,but also provides strong support for participating in the economic scheduling of the IDC.

1 Three-tier optimization framework for IDC

The proposed IDC architecture,including the PV and EUPS clusters,is shown in Fig.1 and mainly includes multiple PV power generation systems,EUPS clusters,server clusters,and an energy management system.

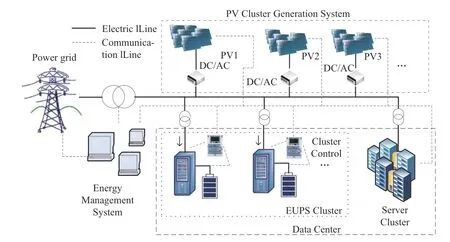
Fig.1 Schematic diagram of IDC

This study adopts the concept of a unidirectional EUPS.It mainly comprises a grid-side converter,load-side converter,and an energy storage unit.In contrast to the traditional UPS,the unidirectionally regulated UPS has an energy-storage function owing to which it can participate in the optimal operation of the IDC and play a key role in inventorying idle resources.Detailed information on the unidirectional regulation of the EUPS can be found in [10].

For a large number of EUPS in the IDC,adopting corresponding methods to realize EUPS cluster aggregation management is an effective way to solve the EUPS control problem.Considering the backup power function of EUPS,using an EUPS to participate in the economic dispatch of the IDC is essential for revitalizing “idle resources” and enabling the IDC to achieve optimal economic dispatch.

This study proposes a three-tier optimization framework for IDCs,that includes EUPS device layer,EUPS aggregation layer,and economic scheduling layers,as shown in Fig.2.First,a classification method for the EUPS cluster based on CSMN is proposed for the EUPS device layer.The characteristic similarities and individual differences of individual EUPSs are considered at this level,and a rational aggregation of the EUPSs is realized.Subsequently,an optimal scheduling model for the EUPS aggregation unit is proposed.A dispatchable charge and discharge power model of the EUPS aggregation unit was established based on the backup power function of the EUPS aggregation layer.Finally,in the economic scheduling layer,the charge,discharge,and aging costs of the EUPS aggregation unit are considered.A minimum-cost economic scheduling model is established,and the QPSO algorithm is used to implement the model,which verifies the economy and effectiveness of the framework and model proposed in this study through multi-scenario cases.

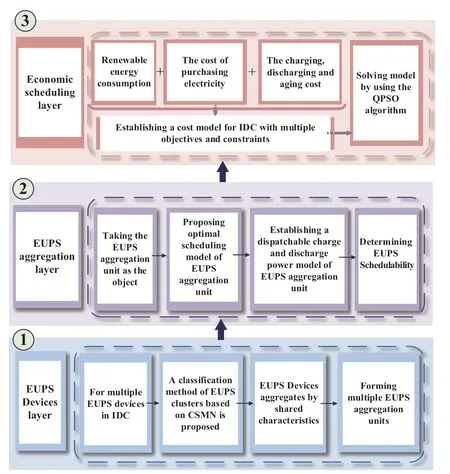
Fig.2 Three-tier optimization framework for IDC

2 EUPS cluster classification method of IDC

The EUPS cluster classification method based on the CSMN proposed in this study was applied to the EUPS device layer.It realizes the aggregation and classification of multiple EUPS,which reduces the unnecessary loss of life of the EUPS.It also solves the EUPS control problem and improves its scheduling capability in an IDC.The implementation of the UPS clustering classification method based on CSMN primarily uses the similarities between individual UPS devices.The fitness of the EUPS device was considered as a shared resource,and the original fitness was adjusted by calculating the degree of sharing between individual EUPS.The EUPS device-sharing fitness method is as follows∶

wherefsh(i) is the shared fitness of the EUPS devices,fit(i)is the original fitness value of the EUPS devicesi,andd(i,j)represents the distance between EUPS devicesiandj,where the average distance are used in this method,shis the shared function between devices that characterizes the similarity of the two EUPS devices.From the above equation,it can be observed that the greater the degree of sharing of an individual device,the smaller its sharing adaptability.

The sharing function in the proposed method indicates the degree of closeness between EUPS devices in the system.In this study,the state of charge (SOC) of the EUPS aggregation unit and the load condition were the key factors affecting the EUPS aggregation unit’s participation in the optimal operation of the IDC.The load condition can also be indirectly reflected in the SOC of the EUPS aggregation unit.Because the SOC of the EUPS is sufficient to represent the dispatchable power of the EUPS at a certain instant,the SOC of the EUPS device is used to represent the degree of closeness of the relationship between individual EUPSs.The shared function can be expressed as

whereδis usually 1;δshis a parameter that controls the size of the niche range,which can be called the niche radius.In this study,the distance between the two devices is denoted as SOCi,jand is the average distance considered in this study.

whereδshis divided into the EUPS overcharge limit,overcharge warning,normal working,overdischarge warning,and overdischarge restriction areas according to the value of SOCi,j.The details are presented in Table 1.

Table 1 Niche radius classification

Here,SOC1is the upper limit of the overcharge warning area;SOC2is the lower limit of the overcharge warning area;SOC3is the lower limit of the normal working area;and SOC4is the lower limit of the overdischarge warning area.

The steps of the EUPS cluster classification method based on the CSMN are summarized as follows∶

1) Obtaining the fitness value of the EUPS of IDC devices,i.e.,the device’s SOC.

2) Determining the number of initial niches,that is,random integerskbetween random initial generations [1,N].

3) The firstkEUPS devices in the EUPS cluster are placed in different niches and become niche centers.The SOC values of the k devices in all the niches were obtained,and the radius interval of the niche where thekniche centers are located is determined.If the niche center belongs to the same niche range,the niche is synthesized;otherwise,a new niche is generated.

4) The average value of the generated device is selected as the center of the new niche.For the remaining EUPS devices in the EUPS cluster,the SOC of the individual EUPS is obtained,and the relationship between the remaining EUPS devices and the newly formed niche center is calculated.Determine whether it belongs to the same niche radius interval,or if it is a synthetic niche.Otherwise,a new niche is generated,which becomes the center of the niche.

5) Classifying EUPS clusters using iterative updates until all the EUPS devices in the cluster are allocated.

3 Optimal scheduling model and dispatchable charge and discharge power model of the EUPS aggregation layer

The EUPS cluster classification method is used to divide the EUPS cluster into multiple EUPS aggregation units.In the later steps the classified EUPS unit is equivalent to one EUPS,and the optimal dispatching model of the classified EUPS unit can be expressed as

whereQE,unitis the capacity of a given EUPS unit after classification,and SOCE,unitis the state of charge of this EUPS unit after classification.μis an integer variable taking values of 0 or 1,whenμ=0,it indicates that the received dispatch instruction is a charging instruction,and whenμ=1 indicates that the received dispatching instruction is a discharge instruction.Each aggregation layer can receive only one instruction at a time and cannot receive charge and discharge instructions simultaneously.

After establishing the optimal scheduling model of the EUPS aggregation unit,it is necessary to ensure the backup power function of the EUPS aggregation unit and then consider the dispatchable charge and discharge model of each EUPS aggregation unit at timet.The relationship between the EUPS backup-power time and the SOC is as follows∶

whereTE,uintis the power backup time of EUPS aggregation unit,QE,uintis the capacity of the aggregation unit,γE,unitis the energy storage attenuation coefficient of the EUPS aggregation unit,andPl,maxis the maximum load power.

From the above equation,it can be determined that

For the convenience of description,s=(SOCE,unit(t+1)-SOCE,unit(t)),h=TE,unit*Pl,max/QE,unit*γE,unit.Whens＞h,the EUPS aggregation unit is discharged;whens＜h,the EUPS aggregation unit is charged.The dispatchable charging and discharging power models of the EUPS aggregation unit can be expressed as

wherePE,unitrepresents the chargeable and dischargeable power of the EUPS aggregation unit at timet;SOCE,unit(t+1) and SOCE,unit(t) represent the state of charge of the EUPS aggregation unit at timet+1;andt,respectively,andQE,unitrepresents the capacity of the EUPS aggregation unit.

4 Minimum cost economic scheduling model for an IDC with PV and EUPS clusters

Here the EUPS aggregation unit is adopted to participate in the optimal scheduling operation of the IDC.It not only ensures the backup power function,but also makes full use of the “idle assets” of EUPS.

4.1 Equivalent model of PV cluster output

PV power generation is mainly affected by temperature and solar irradiance intensity,which are of great uncertainty[21].The PV output model is shown in equation (8).

wherePstis the maximum test power under standard conditions,Gstis the light intensity under standard test conditions,generallyGst=1000 W/m2,Gbis the solar irradiance to which the battery is exposed,kis the power temperature coefficient,Trtis the reference temperature,Tctis the temperature of the photovoltaic cell.

It is defined that the IDC has {1,2,...,B} PVs,and from equation (8),the 24-hour output power of each PV can be obtained.That isPpv1={PV1(1),PV1(2),...,PV1(24)},Ppv2={PV2(1),PV2(2),...,PV2(24)},…,PpvB={PVB(1),PVB(2),...,PVB(24)}.The equivalent model of output power of the PV cluster at timetcan be expressed as

wherePpv,c(t) is the output power of the PV cluster at timetandbis theb-th PV in set B PV.PV(b)(t) is theb-th PV output power at timet.andare the minimum and maximum values of theb-thPV output,respectively.

4.2 Multi-objective function of IDC

The optimal objectives of this study mainly consider the cost of power purchased from the power grid,charge,discharge,and aging costs of the EUPS aggregation units.The minimum-cost economic scheduling model of the IDC can be expressed as

where,[f1(X,υ),f2(X,υ),f3(X,υ)] is the objective function,andg(X,υ) andh(X,υ) are the equality and inequality constraints,respectively.Xdenotes the decision variable.

f1is the cost of purchasing electricity from the power grid and is defined as follows∶

wherePprice(t) is the price of electricity at timet,and the time-of-use (TOU) electricity price can be used here,andPm(t) is the electricity purchased from the power grid at timet.

f2is the charge and discharge cost of the EUPS aggregation unit,and the charge and discharge cost model of the EUPS aggregation unit can be obtained as∶

whereCc,lossandCdc,lossare the charging and discharging power losses of the EUPS aggregation unit,respectively.

wherePc,EUPS,unitis the charging power of the EUPS aggregation unit,andηcis the charging efficiency of the EUPS aggregation unit.

where,Pdc,EUPS,unitis the discharging power of the EUPS aggregation unit,andηdcis its discharging efficiency.

f3is the aging cost model of the EUPS aggregation unit and can be expressed as follows∶

wheredEUPSis the discharge depth at the beginning of the m cycle,Pc,dcis the charging and discharging power of the EUPS aggregation unit,Δtis the control cycle,which can be 1 h;QE,unitrepresents the capacity of EUPS aggregation unit,KEUPSis the characteristic constant of the EUPS aggregation unit,and can be referred to as the characteristic constant of energy storage.It is set to value in the range of 1.1–2.1.N100indicates the number of charge and discharge cycles at 100% depth of discharge of the EUPS aggregation unit,which is equivalent to the number of charge and discharge cycles at 100% depth of discharge of the internal energy storage system.CEUPSis the acquisition cost of the EUPS aggregation unit.

4.3 Constraints

The constraints of the minimum-cost economic scheduling model include the power balance and the upper and lower limits of power.The details are as follows.

1) Power balance constraints

wherePl(t) is the power load at timetin the IDC.

2) Upper and lower power constraints

3) EUPS aggregation unit SOC constraints

In addition,the constraints also determine the limits of energy storage and PV,as shown in the equation (7) and (9).

4.4 Optimization algorithm

From the above analysis,it can be observed that the minimum cost economic scheduling model of the IDC with PV and EUPS clusters is a multi-objective optimal scheduling model with multiple objectives,and multiple equality and inequality constraints.Therefore,the quantum particle swarm optimization (QPSO) algorithm is used to solve the optimization problem.The detailed principles of QPSO can be found in [22-24].

Every particle in the QPSO,which is in a quantum state,can be formulated using the wave function of the Schrödinger equation.Owing to the action of the local attractors,the particles converge to a certain region,which is defined as follows [23,24]∶

whereaandbare the number of particles and dimensions of the solution space,respectively.Here,dddenotes the number of iterations.Sa,b(dd) is the local attractor,andsa,b(dd) is the personal best position of the particle,gb(dd) is the global best position of the swarm.ψa,b(dd) is a random number with uniform probability density function (PDF)over the interval (0,1).

In QPSO,all particle update methods are performed according to equation (22) [24].

In equation (22),Ya,b(dd+1) is the position ofain the(dd+1)thiteration,andδis the contraction-expansion factor that can control the convergence rate of the QPSO algorithm;Bb(dd) is the center of the optimal population position;μa,b(dd) is a random number with uniform PDF over the interval (0,1).ddmaxmaximum number of iterations;Ris the total number of particles representing the potential solution.A flowchart for solving the optimization problem based on QPSO is shown in Fig.3.

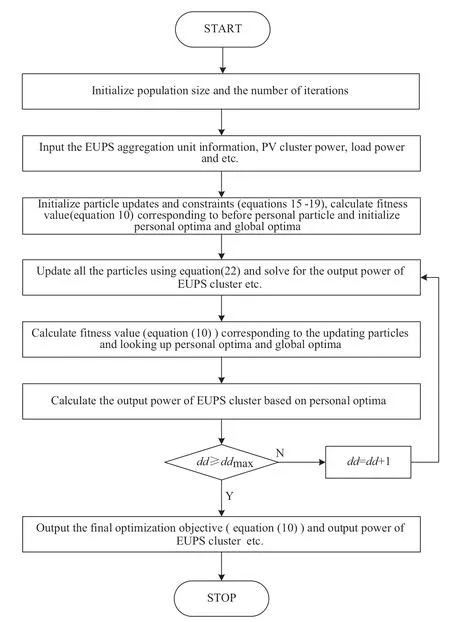
Fig.3 The flowchart of solving based on QPSO algorithm

5 Case study

This study considers an IDC that includes PV and EUPS clusters as an example,and the IDC includes 100 EUPS devices.The random-number generation method was used to generate the SOC information of 100 EUPS devices at a certain moment.The SOC information for the 100 EUPS devices is shown in Fig.4.The output power of the PV cluster and TOU electricity price are shown in Fig.5.Among these,the TOU electricity price adopts the peak and valley commercial electricity consumption in Guangdong Bay Area,China.

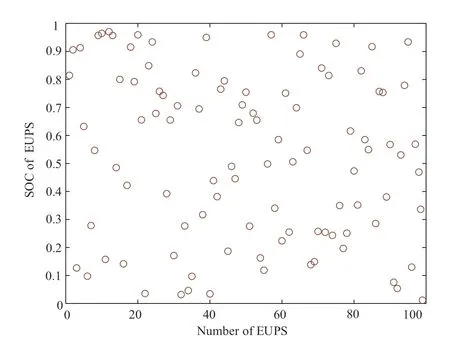
Fig.4 SOC of 100 EUPS in the IDC with PV and EUPS clusters

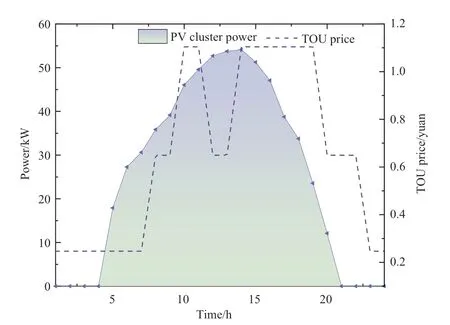
Fig.5 Output power of PV cluster and TOU price

Based on this,we set up a simulation analysis of the following three scenarios∶ Case 1 verified the effectiveness of the EUPS classification method proposed in this study.Case 2 studied the power purchase cost when the EUPS aggregation unit did not participate in the optimization of IDC scheduling.Case 3 studied the impact of EUPS aggregation units participating in the optimization of IDC scheduling on the economic costs.

5.1 Case 1: Validation of EUPS aggregation classification method

In this case,the IDC was used as the background,and the SOC of the EUPS device was used as the shared feature.This classification method is used at the EUPS device layer,and the proposed method is implemented using MATLAB;the simulation results are shown in Fig.6.

Fig.6 EUPS cluster classification

Fig.6 shows the EUPS clustering classification method proposed in this study.It can aggregate multiple EUPS devices based on similarities in characteristics and generate different habitats,depending on the set niche radius.Further,EUPS aggregation units with different characteristics are formed,and finally the aggregation management of the EUPS is realized.In the future,the power,SOH,etc.of the EUPS could be considered as the shared features.

5.2 Case 2: EUPS aggregation unit does not participate in the IDC’s optimal dispatching process

In Case 2,the EUPS aggregation unit did not participate in the optimal scheduling of the IDC.The TOU electricity price also adopts the peak-valley price standard for commercial electricity in the Guangdong Bay Area of Guangdong Province (as shown in Fig.5),and the cluster output power of the PV,load power,and power purchased from the power grid are shown in Fig.7.

Fig.7 Unit output of IDC with PV and EUPS clusters

When the output power of a PV cluster cannot satisfy the load demand,electricity must be purchased from the grid.The cost of purchasing electricity is 1697.0485 yuan per day.

5.3 Case 3: EUPS aggregation unit participates in IDC’s optimal dispatching

In this scenario,the EUPS aggregation unit,formed by the aggregation management of the EUPS device layer,participates in the optimal scheduling of the IDC.MATLAB programming was used to integrate the aggregation model,the dispatchable charge,and the discharge model under the backup function of the EUPS aggregation unit into the IDC optimal scheduling model.Simultaneously,the QPSO algorithm is used to solve the optimal scheduling model.

In this case,the electricity price is based on the TOU electricity price in Guangdong Bay.At present,the EUPS aggregation unit can participate in a dispatching capacity of 300 kWh,the maximum purchasing power with the grid is 150 kW,the SOC corresponding to the EUPS aggregation unit that meets the backup-time requirements is not less than 0.3,the population size is 200,and the number of iterations is 1000.The results are shown in Fig.8,Fig.9,and Fig.10.

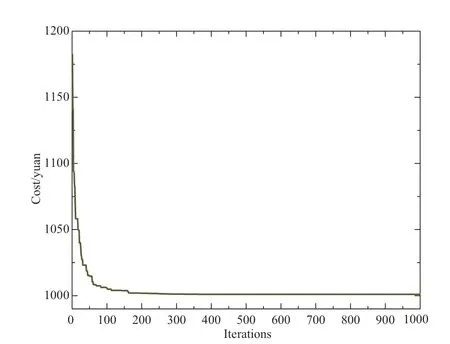
Fig.8 The relationship between the number of iterations and optimum cost

Fig.9 Unit output of IDC with PV cluster and EUPS cluster

Fig.10 SOC value of EUPS aggregation unit

Figure 8 shows the relationship between the number of iterations and the optimization process.As shown,when the number of iterations is greater than 400,the curve is nearly stable,and the optimal objective cost of the final IDC is 1001.0495 yuan.Clearly,the economy of the EUPS aggregation unit participating in the optimal operation of the IDC is better than that of an EUPS aggregation unit that does not participate in the optimal operation of the IDC.The cost of the EUPS participating in the IDC operation saves approximately 696 yuan compared to the cost of the EUPS not participating in the IDC optimization operation.Using EUPS aggregation units to participate in the optimal operation of data centers not only revitalizes idle EUPS resources but also realizes the economic operation of the IDC.

Figure 9 shows the unit output curve when the EUPS aggregation unit participates in the IDC optimal scheduling.As shown in Fig.9,the PV cluster power generation cannot satisfy the load power supply initially,and the EUPS aggregation unit cannot discharge as soon as it satisfies the backup power demand.It is necessary to buy electricity from the power grids.The EUPS aggregation unit can be charged owing to the low electricity selling price of the current grid.When the power generated by the PV cluster cannot satisfy the load demand,it can supply power to the load through the EUPS aggregation unit to ensure the normal power supply to the load.The advantage of this scenario is the increased use of clean energy and the reduced dependence of the IDC on the local grid.

Figure 10 shows the SOC change curve of the EUPS aggregation unit,and it can be seen that the SOC of the EUPS aggregation unit does not fall below 0.3 during the 24-hour operation.At the same time,because of the EUPS cluster classification method based on the CSMN proposed in this study,the EUPS aggregation unit participating in the economic scheduling of the IDC runs within a safe range during the entire operation cycle.This not only ensures the realization of the EUPS backup power function but also proves the effectiveness of the proposed model.

6 Conclusions

This study proposes a new solution for IDCs with PV and EUPS clusters to optimize the use of EUPS resources.Through three case studies,the economy and effectiveness of the proposed method and model under the three-tier optimization framework were verified,and the following main conclusions were drawn∶

1) The EUPS cluster classification method based on the CSMN proposed in the EUPS device layer effectively classifies individual EUPSs based on similarities in their characteristics and forms different aggregation units.The aggregation management of the EUPS in the IDC can solve the EUPS control problem.

2) After forming the EUPS aggregation layer,the proposed optimal scheduling model for the EUPS aggregation unit and the dispatchable charge and discharge model of the EUPS aggregation layer for the backup function ensure that the EUPS can be charged and discharged while realizing the backup power function and promote the EUPS for flexible use of available resources.

3) Based on the proposed optimal scheduling model of the EUPS aggregation layer and the charging and discharging power model of the EUPS aggregation layer for the backup power function,the EUPS aggregation layer formed by applying the application realizes the optimal economic scheduling of the IDC.

In the future,we can comprehensively consider the characteristics and operating characteristics of EUPS to achieve aggregation.In this paper,we establish an aggregation method for EUPS based on the CSMN and only consider the SOC.In the future,we can further consider more critical factors.

Acknowledgments

This work was supported by the Key Technology Projects of the China Southern Power Grid Corporation(STKJXM20200059) and the Key Support Project of the Joint Fund of the National Natural Science Foundation of China (U22B20123).

Declaration of Competing Interest

We declare that we have no conf lict of interest.