Stochastic programming based coordinated expansion planning of generation,transmission,demand side resources,and energy storage considering the DC transmission system

Liang Lu,Mingkui Wei,Yuxuan Tao,Qing Wang,Yuxiao Yang,Chuan He,Haonan Zhang

1.Southwest Branch of State Grid Corporation of China,Chengdu 610065,P.R.China

2.College of Electrical Engineering,Sichuan University,Chengdu 610065,P.R.China

Abstract: With the increasing penetration of wind and solar energies,the accompanying uncertainty that propagates in the system places higher requirements on the expansion planning of power systems.A source-grid-load-storage coordinated expansion planning model based on stochastic programming was proposed to suppress the impact of wind and solar energy fluctuations.Multiple types of system components,including demand response service entities,converter stations,DC transmission systems,cascade hydropower stations,and other traditional components,have been extensively modeled.Moreover,energy storage systems are considered to improve the accommodation level of renewable energy and alleviate the influence of intermittence.Demand-response service entities from the load side are used to reduce and move the demand during peak load periods.The uncertainties in wind,solar energy,and loads were simulated using stochastic programming.Finally,the effectiveness of the proposed model is verified through numerical simulations.

Keywords: Hydro-wind-solar complementary;Expansion planning;Demand response;Energy storage system;Sourcenetwork-demand-storage coordination

0 Introduction

With the depletion of fossil fuels and the continuous expansion of energy demand worldwide,a more severe energy crisis is approaching [1,2].China has been actively promoting energy structure transformation and developing renewable energy technologies for years [3].The 14th Five-Year Plan for Renewable Energy Development was proposed,focusing on carbon peaking and neutrality goals.The Plan targeted that,by 2025,the total accommodation of renewable energy would be equivalent to one billion tons of standard coal,and the increase in renewable energy accommodation would account for more than 50% of the increase in primary energy consumption.As the most important forms of renewable energy affected by the environment,meteorology,and many other factors,wind and solar energy present significant volatility and uncertainty,which pose challenges to power balancing and operational stability of the power system after large-scale integration [5].Energy storage technologies can chronologically transfer renewable energy outputs by strategically storing and releasing energy [6,7].Energy storage systems are essential flexible resources that participate in peak load shaving and frequency regulation,mitigate the intermittence of wind and solar energy,and help reduce the impact of renewable energy on the safe and stable operation of the system.

Capacity allocation of energy storage systems has been widely studied to explore their potential for assisting the operation of emerging power systems.Exploring the characteristics of distributed energy storage systems and considering operational feasibility and planning comprehensiveness,[8] designed a novel bi-objective mixedoptimal planning model for distributed energy storage systems in active distribution networks.Reference [9]studied the relationship between the increasing renewable energy penetration level and the demand for energy storage capacity and found that the latter is strongly positively related to the former;however,a turning point that breaks this positive correlation exists.Considering the uncertainty of wind energy and the maintenance and operation costs of energy storage systems,[10] proposed a method to configure the energy storage capacity to improve system reliability reasonably.Reference [11] proposed a method to mitigate wind energy fluctuations by optimally allocating the capacities of energy storage systems based on an improved moving average and integrated empirical mode decomposition (EEMD).Reference [12] studied a plan for partially replacing conventional thermal units with energy storage systems using a time-series simulation method.The configuration scheme of energy storage systems that can deal with load fluctuations and maximize revenue is considered optimal.However,most existing works focus on allocating the capacities of energy storage systems to realize peak load shaving and frequency regulation and moderate the accommodation challenge with the rapid increase in renewable energy.In summary,the available research on planning models focuses on separate parts of energy storage,neglecting the coordinated expansion planning of generation,transmission,load demand,and energy storage.

Generation and grid expansion planning is conventionally conducted sequentially.Generation planning was conducted first,followed by grid-expansion planning [13].This traditional approach increases the security risks of transmission lines in the context of high renewable energy penetration,affects the scheme,and compromises economic optimality [14,15].Therefore,source-and grid-coordinated expansion planning has been extensively studied [16].Reference[17] reviewed the basic concepts,system operation modes,and critical technologies in source-network-load-storage coordinated optimal operations and proposed a multistage planning model for distribution systems.Reference [18]proposed a novel source-network-load coordinated planning model that combines generation expansion and transmission expansion,particularly considering the regulation ability of the system.Reference [19] proposed a mixed-integer linear programming (MILP)-based robust multi-objective model that considered the retirement of generation units and fuel transportation routes.This model can improve the tolerance of system operation to forecasting errors.

Demand response,which is an essential aspect of demandside management,motivates flexible loads to participate in system regulation by guiding power consumption behaviors[20,21].Moreover,demand response can help in peak shaving and valley filling and promote renewable energy accommodation [22].Reference [23] introduced tiered pricing-based multiple timescale joint demand response and energy storage system planning.By adopting the generationoriented concept of capacity credit,[24] proposed a novel framework to assess the contributions of energy storage and demand response to system power adequacy.Reference [25]proposed a demand response potential evaluation model for industrial users that could evaluate their demand response potential more accurately,thereby facilitating demand response deployment.Based on the coordination of the source network,the long-term expansion planning of the source network-load-storage,considering the characteristics of the demand response,has great potential for dealing with uncertainty.Further research is required in this area.

Through the analysis of literature related to power system expansion planning,it is found that there are the following deficiencies in the long-term planning of power systems with renewable energy∶

(i) Some existing studies have applied source-network coordination planning methods to achieve economically favorable planning results.However,there is limited research on source-network-load-storage coordination planning methods considering demand response.Furthermore,the demand response model applicable to longterm expansion planning requires in-depth investigation.

(ii) In existing studies on power system expansion planning,transmission line models commonly employ a simple DC power flow method,neglecting node voltage security and the impact of power losses on economic considerations.

This study proposed a stochastic programming-based source-grid-load-storage coordinated expansion planning model to promote renewable energy accommodation.The contributions of this study are twofold∶

(i) A stochastic programming-based source-gridload-storage coordinated expansion planning model was proposed considering the uncertainties of renewable energy and loads.

(ii) Multiple types of system components,including demand response service entities,converter stations,DC transmission systems,cascade hydropower stations,and other traditional components,have been extensively modeled.

This study addresses the complexity of power system expansion planning by employing a stochastic planning approach to simulate the randomness of wind and solar power outputs and loads.First,the source-grid-load-storage coordinated expansion planning model considering demand response service is established to minimize expansion planning costs.By incorporating wind and solar curtailment penalty constraints,the model ensures the effective accommodation of renewable energy under conditions of output uncertainty.Finally,the effectiveness of the proposed model is validated through multiple sets of cases.

1 Source-grid-load-storage coordinated expansion planning model

1.1 Objective function

The objective of the source-grid-load-storage coordinated expansion planning model is to minimize the total cost,which consists of the investment cost (IC),the operation cost (OC),and the penalty cost (LC).ICis composed of the cost of building new generator units,new transmission lines,and new energy storage systems.It also accounts for the cost of load demand response service entities.The model only considers traditional generating units on the “source”side for coordinated planning.Investment and planning are not conducted for the converter stations and cascaded hydropower plants.OCconsiders the operation cost of thermal units and energy storage systems.LCincludes the penalties of load shedding and wind and solar energy curtailment.

In (2)–(6),aandtare indexes of hours on a typical day and year,respectively.i,l,e,anddare used to index the thermal units,transmission lines,energy storage systems,and demand response service entities.CG,CL,CEandCDrespectively collect the candidate thermal units,the candidate transmission lines,the candidate energy storage systems,and the candidate demand response service entities,respectively represents the cost coefficients of the four types of facilities.For candidate facilities,yit,ylt,yet,andydtare binary variables representing whether the corresponding candidate facility is planned.Piatrepresents the power output of the thermal unitiat houraof a typical day-of-yeart.Ceis the investment cost coefficient of energy storage systeme.andrepresent the planned charging and discharging capacities of energy storage systeme.whereDTatrepresents the load duration.Fi()⋅ is the cost function of a thermal uniti.Cl,Ce,andCwrepresent the load losses,wind energy curtailment,and solar energy curtailment penalty coefficients,respectively.Dtrepresents the loss of load amount for the yeart.WtandStare the wind and solar energy curtailment amounts for yeart,respectively.κtandddrare the market-value coefficient and discount rate,respectively.

1.2 Constraints

Investment constraints∶ The expansion planning model considers investing in four types of new facilities–thermal units,transmission lines,energy storage systems,and demand response service entities–and considers the retirement of existing thermal units.For a candidate thermal uniti,yitis equal to 1 if it is planned to be constructed,whereas for an existing thermal unit,itsyitis originally 1,but will be set to 0 once it retires in a certain yeart.This logic ofyitis realized as in (7) and (8),whereEGcollects all existing thermal units andrepresents the operation state of the existing thermal unitsi.Therepresents the retirement year of an existing thermal uniti.Similarly,other facilities are constrained by (9)–(11).Retirement is not considered.

System operation constraints∶ The operation constraints of the system level,thermal units,and transmission lines are cast,as shown in (12)–(13),(25)–(30),and (31)–(32),respectively.With an AC power flow model,constraints(12)–(13) enforce nodal-level active and reactive power balances.

In Equations (12) and (13),N b() represents the set of components connected to the busb.PiatandQiatare the active and reactive power outputs of thermal unititypical dayaof yeart;PhatandQhatare the active and reactive power outputs of cascade hydropower plants;PwatandPsatare the active power outputs of wind and solar energy stations;PlatandQlatare the active and reactive power flows on transmission linelat typical dayaof yeart;Peatrepresents the active power output of energy storage systemeat typical dayaof yeart;Pdatrepresents the load demand of demand response service entitiesdat typical dayaof yeart;andrepresent the active and reactive power injection to the AC side of the converter stationc.s(l) andr(l) represent the indexes of the sending and receiving ends of the transmission linel,respectively.

Equations (14)–(15) calculate the active and reactive power flow on existing transmission lines,and Equations(16)–(17) calculate that on candidate transmission lines.Mis an auxiliary big number.

In (14)–(17),ELcollects all existing transmission lines;glandblare the conductance and admittance of the transmission linel,respectively;Vs(l)atandVr(l)atrepresents the voltages of the sending and receiving ends of the linel.Assuming a smallθlat,(18) holds,and considering a secondorder Taylor series expansion.Assuming thatVs(l)atandVr(l)atare close to 1,(19)–(22) can be derived from (14)–(15)∶The active and reactive power loss termsandcan be rewritten as in (21) and (22),allowingVlat=Vs(l)at−Vr(l)at.

a ndare nonlinear.To this end,with a first-order Taylor series expansion,they are linearized as (23)–(24),whereare the points given to linearize(23)– (24).In this study,were set to 1 andwas set to 0.

Constraints (25)–(28) enforce the active and reactive power bounds of existing and candidate thermal units,whereandrespectively represent the active and reactive power upper bounds of the thermal uniti.(29) is the ramp constraint of thermal units.Δirepresents the ramp rate.Constraint (30) calculates the power output of the energy storage system.andrepresent the charging power and discharging power of the energy storage systemeat the houraof the typical day of the yeart.(27)–(28)enforce the line flow limits of existing and candidate lines,whererepresents the flow limit of the linelat the houraof the typical day of the yeart.

Cascade hydropower station model∶ The outstanding regulation ability of cascade hydropower stations can be utilized to suppress the power fluctuations introduced by renewable energy integration.The hydroelectric conversion is modeled as in (33),treating the density of water to 1.In(33),gis the hydropower conversion coefficient,ηhis the generation efficiency,QhatandHhatdenotes the water flow and head.Constraints (34) and (35) are the power output and ramp rate constraints,respectively,whereandare the power upper and lower bounds;and Δhis the ramp rate of hydropower stationh.

Constraint (36) sets the initial stored water volume tovh,0,t.Constraint (37) represents the reservoir water-volume evolution considering the water time delay.

Constraints (38)–(39) represent the constraints on the water discharge and the water volume capacity of hydropower stationh.Constraint (40) converts water volume into a water head.

In(36)–(40),τhrepresents the flow delay coefficient.Qh−1,a−τh,trepresents the generation flow of the generation flow of the previous hydropower station at a timea−τh.andare the upper and lower bounds of generation flow,respectively.andare the upper and lower bounds of the storage capacity,respectively.h0,handαhare constants determined by hydropower stations.Vhatrepresents the storage capacity of a hydropower station andRhatrepresents natural water inflow.

Wind-solar power plants model∶ The outputs of wind and solar plants should be scheduled within the forecasts,as in (41)–(42),whereanddenote the forecasted values of wind and solar power plantswandsat the houraof the typical day of the yeart.

DC transmission model∶ The DC transmission system is modeled as shown in (43)–(47).Constraint (43) sets the upper and lower bounds of the power transmitted through the DC transmission system,and constraint (44) limits the peak-shaving range.Constraint (45) limits the power change over two consecutiveh.Constraint (46) prevents the DC-transmitted power from being adjusted inversely for two consecutive hours per day.Constraint (47) limits the number of power adjustments to within one day.In (43)–(47),andare the upper and lower bounds of the transmitted power,respectively;δarepresents the maximum intraday peak-valley rate;andare the upward and downward power change rates of the transmitted power,respectively;and the binary variablesandrepresent the upward and downward adjusting states of the transmitted power.

Simultaneously,the daily transmission power should satisfy the contract,as shown in (48).

Converter station model∶ Converter stations are modeled using (49) and (50),considering the power balance between the AC and DC sides.As shown in Fig.1,constraint (49)represents the balance between the active and reactive powers that flow in and out of the converter station.Constraint (50) limits power flow from the AC side.

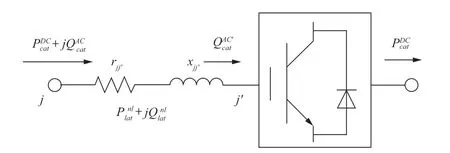
Fig.1 Equivalent circuit of converter

Energy storage system model∶ Energy storage systems can help smooth fluctuations in renewable energy and reduce the intermittent impact of wind and solar energy on power systems.This study focuses on electrochemical energy storage systems and models them,as shown in(51)–(56).Constraint (51) is the stored energy evolution constraint,whereEeatdenotes the stored energy ofeat houraof the typical day-of-yeart;andare the charging and discharging powers ofeat houraof the typical day-of-yeart;andηchargeandηdischargeare the charging and discharging coefficients,respectively.Constraint (52)sets the upper and lower bounds of the storage capacity,whereandare the upper and lower bounds of the energy storage systeme.

Constraints (53) and (54) indicate the upper and lower bounds of charging and discharging power,respectively,whereandare the upper and lower bounds of charging power,respectively;andare the upper and lower bounds of discharging power,respectively;and the binary variablesxchargeandxdischargeindicate the charging and discharging states,respectively.Constraint (55) prevents the simultaneous charging and discharging.Constraint (56) requires that the stored energy at the terminal time interval be equal to the initial energy,whereE0andEHare the stored energies at the initial and terminal hours,respectively.

Demand response service model∶ Demand response,by changing consumption behaviors of loads in the short term,could help promote the accommodation of renewable energy and help ensure the stability of system operation.The demand response service entity is modeled as (57)–(60).Constraint (57) represents the expression of the relationship between planned load,predicted load,and demand response load.whereandPdrrepresent the predicted load and demand response load.Constraint (58) activates a demand response service entity after it is built.Constraint (59)limits the reducible load amount.Constraint (60) limits the total reduced load within a day.In (58)–(60),is the maximum predicted load;βdris the load factor ranging from 0 to 1,andEdr,maxrepresents the limit of the reduced load in a day.

1.3 The expansion planning model in the compact form

For convenience,the deterministic expansion planning model above is written in a compact form,as in (61)–(64).(63) represents all investment constraints,and (64)represents all operation constraints.xrefers to the vector of all binary variables andyrefers to the vector of all continuous variables.A,a,f,m,andnare the corresponding coefficient matrices and vectors,respectively.

2 A source-grid-load-storage coordinated planning model considering uncertainty

2.1 Uncertainty modeling

The accurate values of wind energy,solar energy,and loads can be considered as the corresponding predictions superimposed by the prediction errors.

The uncertainty model of wind energy can be expressed as∶

wherePwat,prepresents the predicted output of a wind farm and ΔPwat,prepresents the prediction error,which generally follows a normal distribution with a zero mean and standard deviation ofσwat,as in (66),whereχ% is the proportion coefficient ofσwatto the predicted wind power.

Similarly,the uncertainty model of solar energy can be expressed as∶

wherePsat,prepresents the predicted output of a solar station and ΔPsat,prepresents the prediction error,which is considered to follow a normal distribution with zero mean and standard deviation ofσsat,as in (69),whereδ% is the proportion coefficient of the standard deviationσsatto the predicted solar output.

In this study,the load fluctuation was considered to follow a normal distribution with the mean ofPdat,pand standard deviation ofσdat,as shown in (71).

whereε% represents the proportion coefficient of standard deviationσdatto the predicted load.

2.2 Scenario generation and reduction

Many scenarios were generated using Monte Carlo simulations with the predicted output and error distributions of wind energy,solar energy,and loads.

More scenarios could help achieve a higher scheduling accuracy but at the same time cause a heavy computational burden;therefore,a fast-forwarding scenario reduction method that reduces scenarios with the smallest distance from all other scenarios until a certain number of scenarios are selected is adopted to make the tradeoff between accuracy and computational burden.A flowchart of the scenario generation and reduction processes is shown in Fig.2.

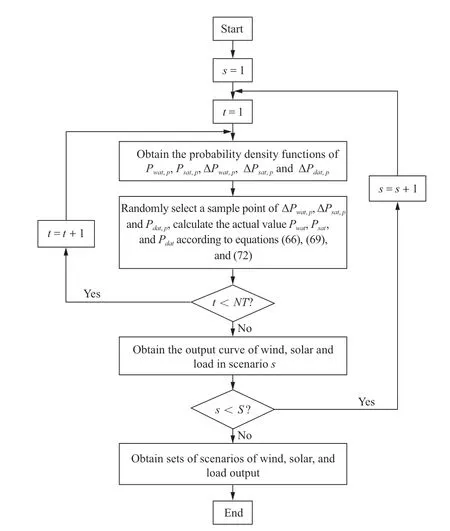
Fig.2 Monte Carlo-based scenario generation method

2.3 Stochastic programming-based expansion planning model

In the proposed stochastic-programming-based expansion planning model,constraints (61)–(64) are revised to (73)–(76) to incorporate scenarios that consider the uncertainty of renewable energy and loads.

In (75)–(76),ysas the counterpart ofybecome scenario dependent andρsis the possibility of scenarios.In each scenario,the generation units must satisfy operational constraints.

The solution framework of the proposed model is illustrated in Fig.3.It can be transformed into a mixedinteger linear planning model and solved using GUROBI to yield optimal planning results.The overall system diagram is shown in Fig.3.

Fig.3 Expansion planning system diagram

3 Case studies

3.1 The test system

To verify the effectiveness of the proposed sourcegrid-load-storage coordination expansion planning model,a modified IEEE 24-node system is used.The existing facilities in the modified IEEE 24-node system include 26 thermal units,38 transmission lines,three wind farms (buses 5,13,and 14),two solar energy stations (buses 4 and 13),three cascade hydropower stations (buses 2,13,and 14),four energy storage systems (buses 7,13,15,and 16),and 17 power loads.The penalty costs for wind and solar power curtailment were set as 1000 yuan/(MWh),the loss of load penalty was set as 105yuan/(MWh),and the participation rate in the load demand response was set as 2%.A total of 19 candidate thermal units,17 candidate transmission lines,and 18 candidate demand response service entities were considered.The duration of the expansion plan was five years.The initial load,wind,and solar energy capacity were set to 3000 MW,720 MW,and 500 MW,respectively.The annual load increase rate was 4%,and the wind and solar energy capacity increase rates were 8%.The upper and lower bounds of the DC transmission system delivered power of 300 MW and 50 MW,respectively.The daily contract volume was 5000 MWh.A typical daily load profile,wind energy output curve,solar energy output curve,and hydropower output are shown in Fig.4.

Fig.4 Power load on a typical day and the output curve of wind and solar energy

3.2 Analysis of simulation results

Four cases were designed to fully validate the complementary regulation effect of cascade hydropower on wind and solar output,the influence of demand response service on load peaking,the promotion effect of energy storage systems on new energy consumption,and the impact of uncertainty considered by stochastic programming on the planning results.

Case 1∶ Deterministic power system source-grid-load planning model without considering energy storage systems and demand response service entities.

Case 2∶ Deterministic power system source-grid-loadstorage planning model.

Case 3∶ A stochastic programming-based source-gridload planning model that does not consider energy storage systems and demand response service entities.

Case 4∶ Stochastic programming based source-grid-loadstorage planning model.

Table 1 summarizes the expansion planning results for cases 1-4.In the table,G,L,and D represent thermal units,transmission lines,and demand–response service entities,respectively.The subscripts indicate the number and number of years of construction.For example,G1,2indicates that a candidate 1 thermal unit is planned for construction in the second year.

Table 1 Expansion planning results of cases 1-4

The loads and thermal unit outputs during the peak load period in case 1 are shown in Table 2.The DC transmission system transmitted power and wind and solar energy curtailment are listed in Table 3.

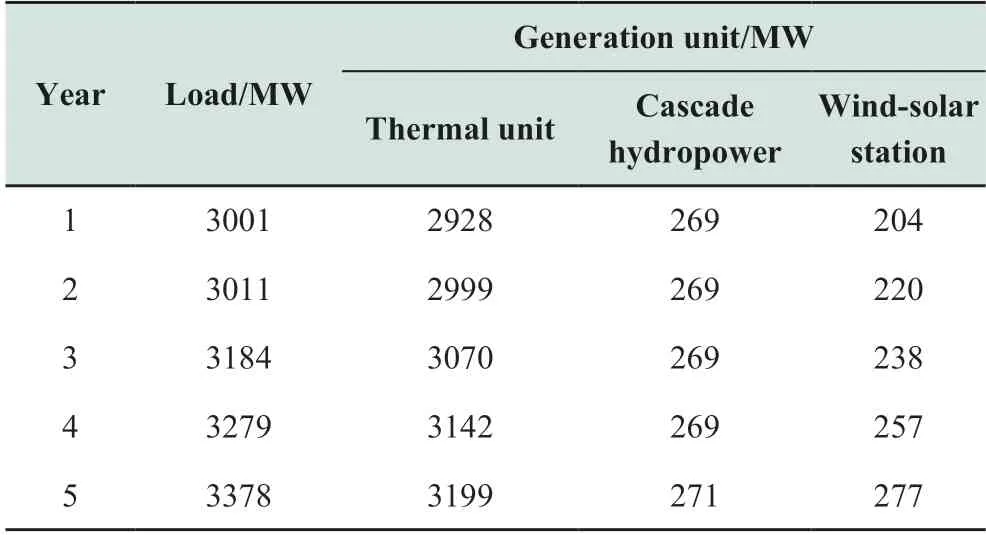
Table 2 Load and generation output during the peak load period

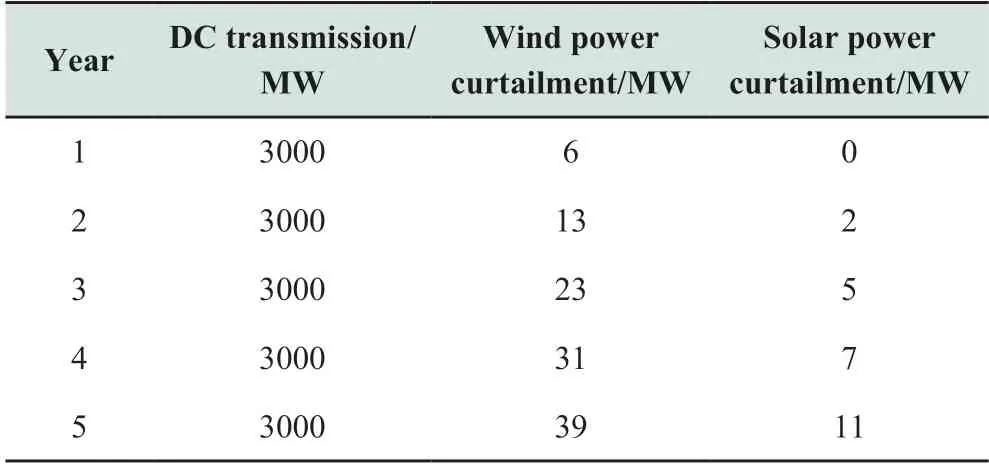
Table 3 DC transmission power and wind-solar power curtailment in Case 1

In Case 1,seven thermal units with a total capacity of 815 MW are retired sequentially within the planning horizon.To meet the load demand,six candidate thermal units with a total capacity of 775 MW were operated starting in the third year.Starting in the third year,to prevent transmission line congestion,the transmission grid was expanded by building four transmission lines with a total capacity of 700 MW.The load demand and generation mix for the fifth year are shown in Fig.5.

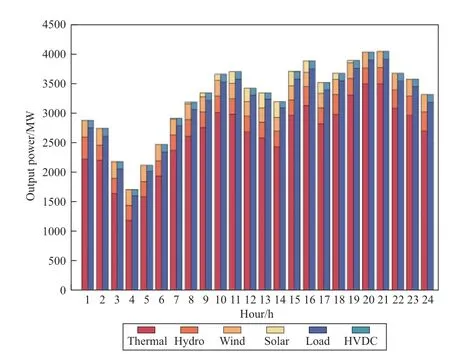
Fig.5 Load and generator output in case 1

Because Case 1 considers source-grid-load planning without energy storage systems and demand response service entities,renewable energy cannot be fully accommodated when the load demand and contracted power transfer quantity through the DC transmission system are met,resulting in significant wind and solar power curtailment and the corresponding penalty cost.

In Case 2,the demand response cost is 600 yuan/(MWh),the daily demand response limit is 1000 MW,and the demand response participation rate is 5%.

The energy storage system stores the remaining renewable energy generated during the valley load period and releases it during the peak load period.Utilizing the flexibility of an energy storage system to shift the output curve can promote the accommodation of renewable energy.The participation of energy storage systems and demand response service entities enables the system to operate safely and stably.Under the premise of delivering the daily contracted volume,wind,and solar power curtailments are reduced to the maximum extent with the coordination of energy storage systems and DC transmission systems.The penalty costs for wind and solar energy curtailment are correspondingly reduced.The demand response service entity can share the pressure on the thermal units by providing a load response during the peak-load period.The results of the source-grid-load-storage planning model considering the demand response service entities during the peak load period are listed in Table 4.

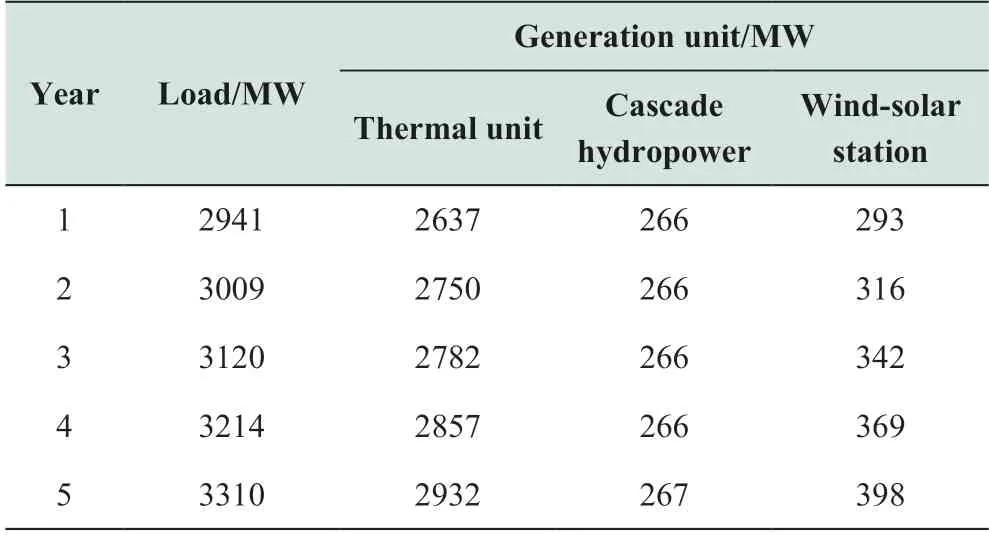
Table 4 Load and generator output during peak period

In Case 2,the renewable energy output is higher than in Case 1.Using the energy storage system to store the remaining energy after meeting the load demand during the valley period,the wind and solar energy curtailment is close to zero,and thus,the total penalty is considerably reduced.The load profiles for Cases 1 and 2 are presented in Fig.6.

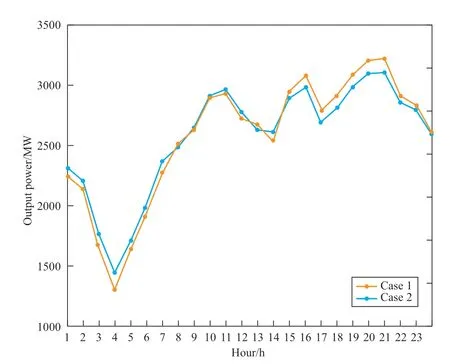
Fig.6 Load curves between Case 1 and Case 2

When the peak load demand exceeds 2500 MW,the demand response service entity actively participates in the regulation,moving the load demand above 2500 MW to the valley load period.

In Case 2,five candidate thermal units with a total capacity of 725 MW are planned.Two candidate demand response service entities are planned to provide more flexibility from the demand side to satisfy the increased load demand.Compared with Case 1,the construction of energy storage systems helps maximize renewable energy accommodation.The load demand and generation mix for the fifth year are presented in Fig.7.

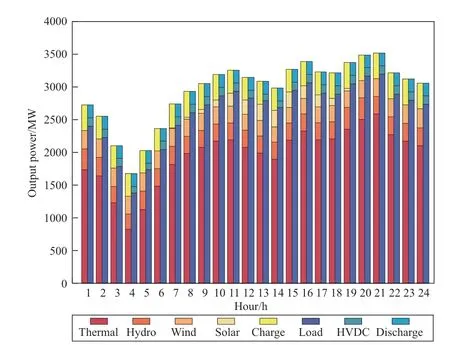
Fig.7 Load and generator output in case 2

The reduced load during the peak load period is transferred to the valley load period through the demand response service,thereby maintaining a balance between the load demand and power generation.As the load increases annually,the action of demand response service entities increases annually,reaching 150 MW in the fifth year.Investment in demand response service entities can help delay the expensive expansion of generation units and transmission lines.

In Cases 3 and 4,stochastic programming was used to simulate the uncertainty of wind,solar energy,and load demands.In Cases 3 and 4,the proportion coefficients of the standard deviation were set to 5%.In total,1000 scenarios were generated and reduced to five typical scenarios using the fast-forward method.

Owing to the uncertainty of wind and solar energy,in Case 3,six candidate thermal units were constructed starting from the second year to meet the uncertain load demand and ensure the safe and stable operation of the system.Six candidate thermal units were constructed starting from the second year.These thermal units will be built one year earlier than in Case 1,and the total capacity will increase to 850 MW.Four candidate transmission lines will be put into operation in the third year with a total capacity of 750 MW.The candidate generation units invested in earlier years provided the system with more flexibility during the peak load period.This investment strategy can smooth the power fluctuations caused by the uncertainty of renewable energy penetration,ensuring system operational safety.An increase in the total capacity of the planned generation units can avoid the high penalty cost caused by load loss.However,owing to the lack of energy storage systems,the accommodation level of wind and solar energy is still low,and high curtailment still occurs.The total costs in Case 3 increased by 5.3% compared to Case 1.

The comparison of the scenarios shows that the larger the proportion coefficient,the greater the error between the actual and predicted values.Accordingly,the capacity required to cope with uncertainty will be larger,leading to further investment in facilities and a higher cost.

Case 4 improved the renewable energy accommodation level by investing in energy storage systems.During the valley load period,the remaining renewable energy is partially accommodated by the ESSs after satisfying the load demand and is released during the peak load period.The maximum values of wind and solar outputs in the fifth year in Case 4 are 319 MW and 240 MW,respectively.To reduce the penalty cost caused by renewable-energy curtailment,the total capacity of the energy storage system increased to 400 MW.The load profile for the fifth year and the output of the generation units in Case 4 are shown in Fig.8.

Fig.8 Load and generator output in case 4

The maximum load demand in the fifth year reached 3481 MW,an increase of 103 MW compared to Case 1.A conservative investment strategy was adopted in Case 4 because of the high penalty cost of load loss.The candidate capacity of the thermal units was increased to 800 MW,and the output limit of the demand response service was increased to 1200 MW.However,the investment cost increases slightly,whereas the total cost is significantly reduced compared with Case 3,which shows considerable progress in economic optimality.

To investigate the impact of forecast errors on the power system planning results and total costs,cases 4.1-4.3 are set based on case 4∶ The proportion coefficients are listed in Table 5.

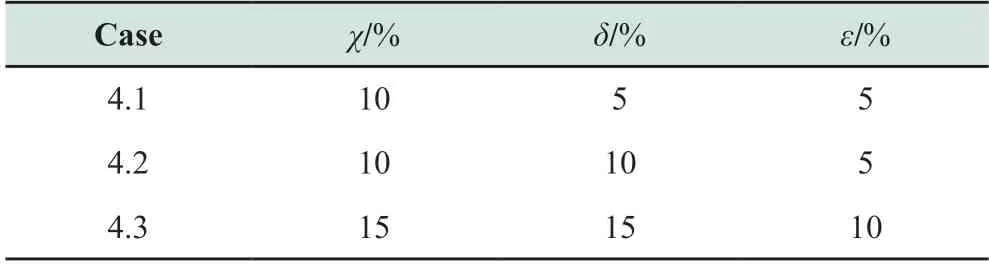
Table 5 Proportional coefficients in Case 4.1-4.3

The curves of wind and solar energy output and load demand in cases 4.1-4.3 are shown in Fig.9.Table 6 lists the relationship between the total costs under different prediction errors.It can be observed that with an increase in the prediction error,the total cost also increases,mainly driven by the penalty cost.

Table 6 Planning results of Case 4.1-4.3

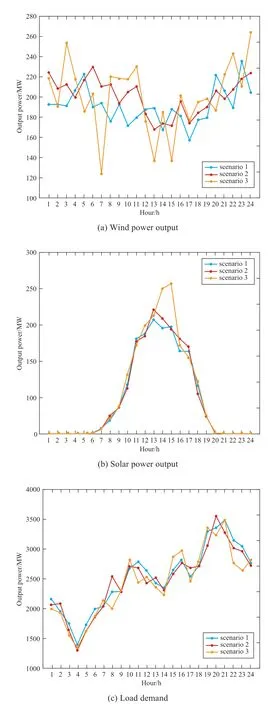
Fig.9 Wind and solar energy output and load demand for each scenario in Case 3

4 Conclusions

To promote the accommodation level of renewable energy,a source-grid-load-storage coordinated expansion planning model was proposed in this study.The uncertainties in wind,solar energy,and loads were simulated using stochastic programming.Through the case study,the following conclusions can be drawn∶ 1) with the demand response service entities,the loss of load can be reduced,and thereby,middle-and long-term costs can be reduced;2) energy storage systems can significantly improve the capacity of renewable energy accommodation,and the demand response service entities can effectively delay the construction of generation units,and 3) the stochastic programming approach considers the uncertainty of wind and solar output as well as load demand.Planning costs must increase relative to deterministic cases to ensure operational flexibility to cope with uncertainty.The expansion planning model effectively considers wind and solar energy curtailment and load shedding,providing an optimal expansion plan that meets the safety requirements for the system.4) As prediction errors continue to grow,the impact of the uncertainty of wind and solar output and load demand on system operation becomes more pronounced.Therefore,in the later stages of planning,there is a need to invest more in thermal units,transmission lines,and demand response service facilities to enhance renewable energy accommodation while ensuring system reliability.

Acknowledgements

This study was supported by Science and Technology Project of SGCC (SGSW0000FZGHBJS2200070).

Declaration of Competing Interest

The authors have no conflicts of interest to declare.