依托单元微专题 促进学生深思考——以解“爪形”三角形微专题为例

张 科 (邮编:730100)

甘肃省兰州市榆中县恩玲中学

骆妃景 (邮编:523000)

广东省东莞市麻涌中学

“爪形”三角形是指在给定的一个三角形中,连接一个顶点和对边上的任意点构成的图形.“爪形”三角形问题是近年来高考数学的热点问题和高频考点,在高考中属于中等难度试题,备受高考命题者的青睐.文章尝试构建“爪形”三角形微专题.从一道经典“爪形”三角形问题开展,通过一题多解拓展学生的数学思维,通过一题多变,促进学生深度学习,让学生从一道题看到一类题,举一反三,触类旁通,深化解决“爪形”三角形策略的思想方法,助力高三复习减负增效.最后给出“三新”背景下高考备考中解三角形教学的几点反思,以便达到精准备考、高效备考,与各位同仁交流探讨.

1 回顾高考 把握趋势

纵观近三年高考数学解三角形问题,大多以“爪形”三角形为载体,主要以方程思想为核心,考查正弦定理、余弦定理以及三角形面积公式,间接考查三角恒等变换、三角函数、不等式等相关知识.尤其是2023年高考四套全国卷中解三角形问题共有6道(新高考Ⅰ卷第16、17题,新高考Ⅱ卷第17题、甲卷理科第12、16题、乙卷理科第18题). 可见,“爪形”备受高考命题者的青睐.

表1

2 课前热身 唤醒认知

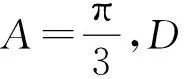
解所以在△ABD中,设AD=x,解得x=2.因为D为AD的中点,所以b=2x=4.

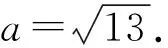
评注本题比较简单,利用正、余弦定理解决由已知元素定量计算其他元素,一般情况下优先解决已知三个元素的三角形,在学生最近发展区设置容易题以便唤醒学生解三角形知识.

3 深度思考 探究策略

图1

方法一(基于边):

设DC=x,BD=2x,AC=y,

在△ABD中,设∠ADB=α,

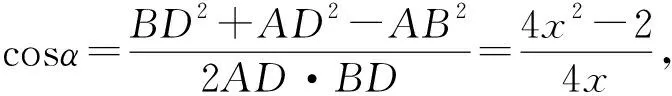
在△ADC中,设∠ADC=β,即

由α+β=π,所以cosα=-cosβ,即

①

在△ABC中,根据余弦定理得:BC2=AB2+AC2-2AB·ACcos∠BAC,

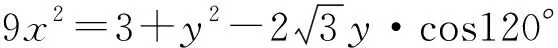
②

评注抓住了三角形的∠ADB与∠ADC互补这一典型特征,通过cos∠ADB=-cos∠ADC分别在两个不同三角形中运用余弦定理列方程组求解.特别地,若D为BC的中点,即为中线定理AB2+AC2=2(AD2+DC2).

变式训练1(2021年新高考Ⅰ卷第17题改编).如图1,记△ABC的内角A、B、C的对边分别为a、b、c,已知b2=ac,点D在边AC上,BD=b,AD=2DC,求cos∠ABC.

在△ABD中,由余弦定理得

在△CBD中,由余弦定理得

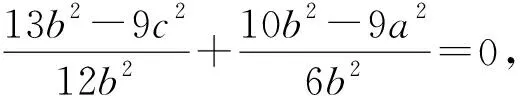
所以b2=ac,所以3c2-11ac+6a2=0,

在△ABC中,由余弦定理得

在△ABC中,由余弦定理有BC=3.

评注《普通高中数学课程标准(2017年版2020年修订)》明确要求“借助向量的运算,探索三角形边长与角度的关系,掌握余弦定理、正弦定理.能用余弦定理、正弦定理解决简单的实际问题.”因此引导学生应用向量解决几何问题,让学生掌握平面几何的向量方法.把所要求解的量转化为基底表示,一般选择已知夹角或模长的不共线向量作为有效基底.

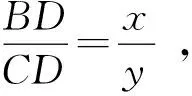
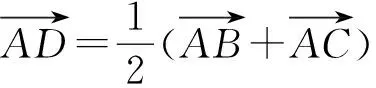
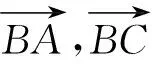
在△ABC中,由余弦定理得AC=3.

方法三(基于角):观察图形中已知三角形和未知三角形中的元素关系,求边长BC可先求BD,因此目标三角形,△ABD中已知两边,需再求一个角方能解决.

设∠BAD=θ,∠DAC=120°-θ,

①

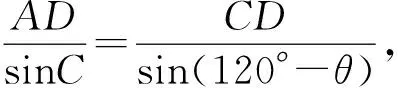
②

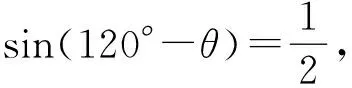
在△ABD中,BD2=AB2+AD2,解得BD=2,故BC=3.

评注波利亚说:“为了得到一个方程,我们必须把同一个量以两种不同的方法表示出来,即将一个量算两次,从而建立相等关系.”这就是“算两次”原理,又称富比尼原理.本解法利用两个三角形中的公共角或者公共边,根据两次正弦定理列方程或两次余弦定理列方程组,揭示了“算两次”原理在解三角形试题中的应用.

变式训练3如图2,平面凹四边形ABCD,其中AB=3,BC=5,∠ABC=120°,ADsinA=CDsinC．证明:BD为∠ABC的角平分线．

图2

①

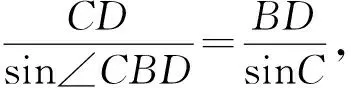
②

联立①②结合ADsinA=CDsinC,得sin∠ABD=sin∠CBD,即BD为∠ABC的角平分线．

方法四(面积法):

由BD=2DC,即S△ABC=3S△ADC, 设∠DAC=θ,则

所以∠BAD=120°-30°=90°.

在Rt△ABD中,BD2=AB2+AD2=4,

所以BD=2,即BC=3.

方法五(面积法比或面积和):

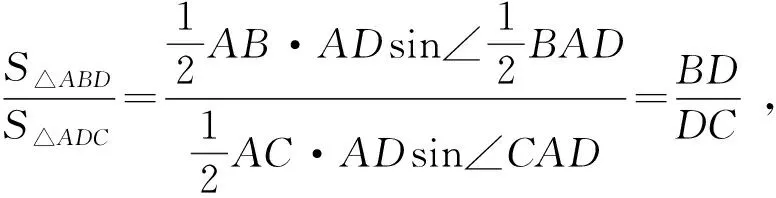
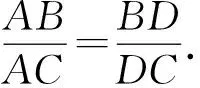
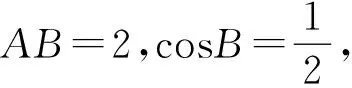
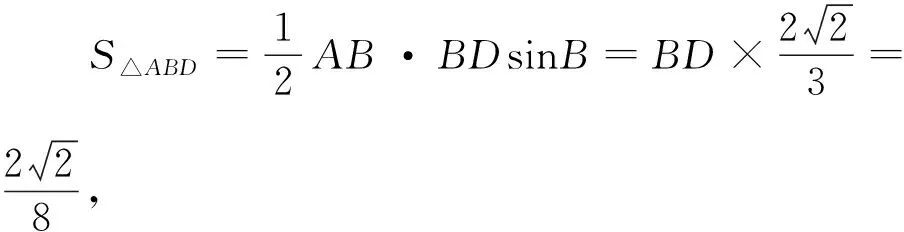
所以BD=4,即BC=6,

在△ABC中,由余弦定理得,

AC2=AB2+BC2-2AB·BCcosB=32,

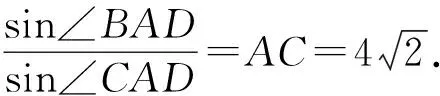
变式训练5(2020山东卷改编):如图1,在△ABC中,内角A,B,C的对边分别是a,b,c,∠ABC=120°,BD是∠ABC的角平分线,交AC于点D,且BD=1,求4a+c的最小值.

解因为∠ABC=120°,BD是∠ABC的角平分线,所以∠ABD=∠CBD=60°.

由三角形的面积公式可得

化简得ac=a+c,

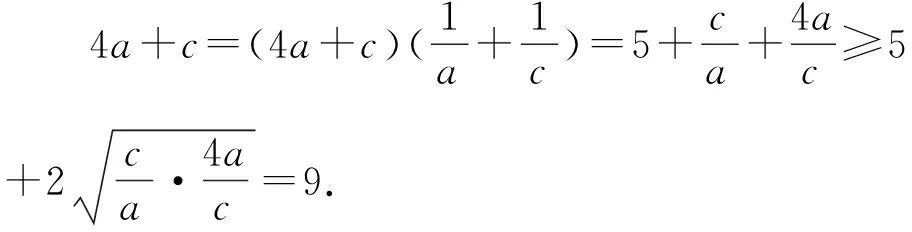
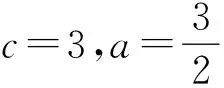
方法六(建系法):

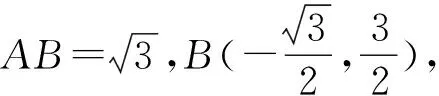
图3

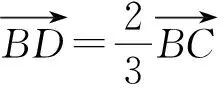
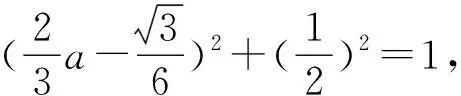
评注充分利用几何图形中的垂直关系建立平面直角坐标系,使得尽可能多的点落在坐标轴上,这是建系的原则.建系后,点坐标化,未知点则需要假设,然后将条件和结论都翻译成坐标形式,根据解析几何知识进行处理即可.

图4

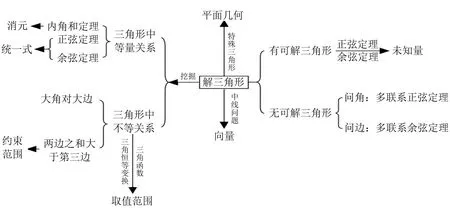
图5

(1)求∠BAM的正弦值;

(2)求∠MPN的余弦值．

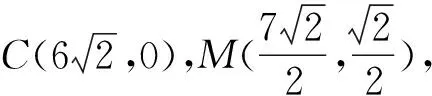
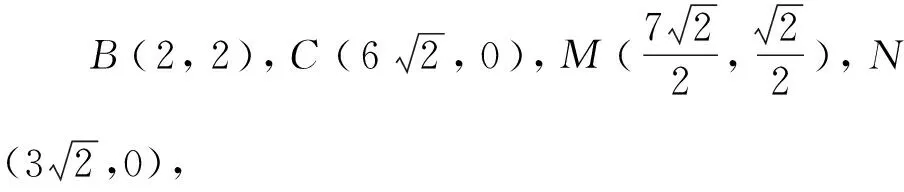
4 高考链接 拓展思维

(2)若b2+c2=8, 求b,c.

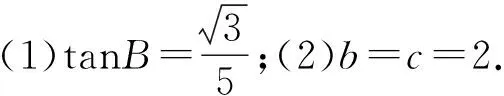
答案2．

(3) (2023年高考乙卷理科第18题)在△ABC中,已知 ∠BAC=120°,AB=2,AC=1.

(1)求sin∠ABC;

(2)若D为上一点,且∠BAD=90°, 求△ADC的面积.

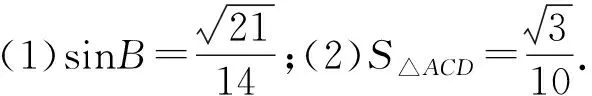
(4) (2023年新高考全国Ⅰ第17题)已知在△ABC中,A+B=3C,2sin(A-C)=sinB,

(1)求sinA;

(2)设AB=5, 求AB边上的高.

5 反思提升 深度教学

在素养导向下的数学教学中, 教师应该坚持“三线”——核心价值为金线,能力素养为银线,情境载体为串联线,引导学生从“解题”到“解决问题”, 从“做题”到“素养”的提升, 笔者认为应做到以下三点:

5.1 精选素材 一题多解——立足深度的教

好的教学素材是一堂课成功的关键.本文典例是“爪形”三角形中开展“一题多解”将零散的知识、方法串点成线、织成网、铺成面,帮助学生构建知识体系最好的素材,试题的难度中档偏下,有利于提高学生的课堂参与度,能取得更好的教学效果.然后在学生深刻理解问题的基础上,从基于边、基于角、向量、面积、建系的角度,帮助学生构建新知地图和方法链接,彰显数学思维发展的流畅美与结构美.

5.2 立足典例 巧创变式——立足深度的学

本节课立足典例、解法,在进行题型训练和拓展变式的主体要求下始终不脱离基础知识的落实和巩,重视学生在课堂中的再体验及巩固,“一题多解”不是教师的表演秀,天花乱坠的地向学生展示多种解法,也不纯粹是学霸们的展现平台.“一题多解”教学中教师不但要引导学生“怎样想到的、为什么这么想、遇到哪儿些问题可以这样想”等,还要让学生经历再体验一次解题活动,本课通过精编变式1～6,以转化思想为主线,串联孤立问题,纵横整合形成变式问题链,引导学生及时跟进巩固练习,内化课堂解题方法,提高一题多解,深度教学的效益,学生内化在教师的指导下再创造解题体验,学生更容易记住和迁移解题经验,形成一定的解决此类问题的能力,发展核心素养.

5.3 聚焦通法 整合联系——立足深度的悟

本节课从经典问题出发,形成模型,确定主问题,变为新问题,注重数学的整体框架,让学生在一轮复习中系统掌握学科基础知识、基本技能、基本方法,在思考过程中给学生一个基本的逻辑思考框架,从类比、联系、特殊化、一般化角度开展数学研究.解三角形问题的知识方法框架如图: