人教A 版高中数学教材文本编写特点研究
——以“弧度制”为例
王运思
《普通高中数学课程标准(2017 年版2020 年修订)》(以下简称“新课标”)在课程性质中指出:“高中数学课程具有基础性、选择性和发展性”,并提出了“学生发展为本,立德树人,提升素养”的基本理念[1]。依此课标理念编写的人教社2019 年版的《普通高中教科书数学A 版》(以下简称“人教A 版教材”),和以前使用的版本相比有了很大不同。比如,不再采用模块化的形式编排知识点,有些章节顺序有所调整,内容也有所增删,等等。除了这些宏观层面的变化外,还有一些微观上的改变,尤其是具体到某一个概念、公式、定理的引入和获得方式的文本编写上,教材有了明显的不同。
一、教师对教材的期望
教材是教师教与学生学的蓝本。对学生而言,希望通过教材的文本描述来理解数学知识,以培养自主学习的能力,为后续发展和终身学习创设条件与机会。对教师来说,由于在教学设计时既要源于教材又要根据学情进行二次开发,有时还需要创造性地重构,因此,教师期望编写者在编写教材时能合理处理好以下几个关系。
(一)学术形态与教育形态的合情转化
众所周知,数学知识从诞生、发展直至成熟,经历过很长时间,期间又要经过“火热的思考”,可这些历程不可能出现在教材中,因此数学知识在教材中只能是以“压缩形态”存在,“准确的定义、逻辑地演绎、严密的推理”进行形式化表述,故教材呈现的数学知识是“冰冷的美丽”,这就是数学知识的“学术形态”。然而在教学过程中,教师还需要对教材中的数学知识进行“解压缩”,将它们还原成学生能接受和理解的知识,因此教师经过备课后在课堂上呈现的数学知识是“教育形态”。为了能让教师高效地使用教材,在编写时可以考虑将数学知识的“学术形态”在文本表述上能合情地转化为“教育形态”。
(二)逻辑序与历史序的恰当选择
数学教材的知识点是按照数学知识结构的逻辑顺序来编排的,因为要将一个新的数学知识讲授给学生,必须完整地从定义、性质、应用等流程展开。然而知识的“历史形态”并非如此一帆风顺,中间可能有许多变化和挫折。比如函数概念[2],历经300 多年才完善,数学家在不同时期对函数的不同认识是没办法在教材上呈现的,只能直接以现在最完善的函数定义呈现。因此编写者在考虑数学知识的逻辑顺序时还要恰当兼顾历史顺序。
(三)科学性与人文性的和谐共处
数学是一门严谨的学科,知识的科学性是编写者首先要保证的。与此同时,数学知识在其发展过程中还有许多人文的一面,比如数学精神、语言、方法、观点等数学文化层面的人文活动。因此,在教材的文本编写中融入数学文化,将数学的人文性也呈现出来,与科学性和谐共处,使两者水乳交融,把数学从知识学习提升到文化熏陶,继而提升到育人的境界。
二、教材文本编写的新特点
笔者对高一、高二的《必修》《选择性必修》共5 本教材的文本内容作了详细研究,发现了许多新的特色,比如课后的习题增多且层次分明,增添了“文献阅读与写作”栏目等,这与一线教师所期望的编写要求相吻合,尤其是每章节的具体文本编写。下面以“人教A 版教材”《必修第一册》5.1节“弧度制”概念为例,通过窥一斑知全豹,冀盼得出教材的文本编写新特点。
(一)文本详实,逻辑连贯
教材的文本编写非常详细,包括情境引入、概念说明、定理解释等,同时在新知的引入、概念的获得、公式的推导等逻辑安排上也更顺畅连贯,符合初学者的思维习惯。
1.弧度制概念引入的文本
让学生接受一个新知识,首先要说明为何要学这个新知,即学习的必要性,然而再讲清楚其合理性,做到“有理有利有节”。比如,弧度制概念的引入。“度量长度可以用米、英尺、码等不同的单位制,度量质量可以用千克、磅等不同的单位制。不同的单位制能给解决问题带来方便。角的度量是否也能用不同的单位制呢?能否像度量长度那样,用十进制的实数来度量角的大小呢?”[3]这段文本有三个层次。第一句以学生熟悉的生活中的例子来切入,情境处在学生的最近发展区,并告诉学生度量可以存在不同的单位,这是第一层次;第二句话承上启下,告诉学生学习不同单位的好处,同时也暗示教师备课时可以适当举例说明,这是第二层次;最后两个疑问句,既告诉学生也告诉教师,可以采用类比的思想进行新知学习,同时还指明了思考方向,可类比长度单位,也启示教师备课时还可进一步深入挖掘,这是第三层次。
虽然对于弧度制必要性的说明还没有到位,但文本中的疑问句却给了教师重构的启发。比如,教师可以给学生设计一个数学问题,让学生发现用原来所学的角度制已无法解决,从而产生认知冲突,让学生意识到只有学习新知识才可以解决。
2.弧度制概念获得的文本
教材在弧度制概念的获得上也着墨较多。教材先给出角度制概念,接下来另起一段:“下面介绍在数学和其他科学研究中经常采用的另一种度量角的单位制——弧度制。”[3]然后用两个同心圆中的扇形相似开始推导和探究,此处文本的表述很具体详细,并且还在旁边配图说明,因而很清晰,也易于学生自学理解。最后得出:“这个比值随α的确定而唯一确定。这就启发我们,可以利用圆的弧长与半径的关系度量圆心角。”[3]至此,才另换一段给出弧度制的定义。
显然,教材的文本编写是从学生已有的认知出发,即从初中所学的弧长公式入手,通过变形得出角一旦确定后的不变性。这样的文本表述,逻辑是连贯的,思维是流畅的,结构是合理的,做到了事出有因、理出有据,为弧度制定义的合理性作了很好的说明,既有利于学生自学,也有利于教师深入挖掘,表明了数学不仅是讲逻辑的,更是讲道理的,也很好地做到了学术形态与教育形态的合情转化。
(二)问题引领,思维自然
美国数学家哈尔莫斯说:“问题是数学的心脏。有了问题,思维才有方向;有了问题,思维才有动力;有了问题,思维才有创新。”数学教学的本质是数学思维活动的教学,因此使学生有疑问能思考才是成功的教学。教材有一个显著的文本编写特点,是“问题引导学习”[4],不仅在教材的章节引言、正文等设置了许多类型丰富的问题,而且在“观察”“思考”“归纳”和作为旁注的“小贴士”中都设置了问题,包括正文后面的“探究与发现”“阅读与思考”也设置了问题。这样的文本编写为教师采用问题链教学提供了很好的问题源泉。
数学问题链是教师在课堂上呈现给学生一系列有序的主干数学问题和辅助问题(子问题),而教材每节内容中的问题安排就是按学生接受新知的逻辑顺序展开的,非常有利于教师的问题链教学设计。笔者从认知水平的角度将教材中的问题进行分类,并对具体呈现方式作了统计,再结合相应的数学问题链,就能一目了然地实施教学,具体见表1。

表1 教材中的问题形式
在“弧度制”一节中设置的“思考”“探究”类问题可作为问题链中的主干问题,即作为解决问题构建新知的关键核心问题,其余则可作为从属的子问题。当然,这些问题并不是孤立的,一个问题链中有若干子问题,它们环环相扣、链链相套,将知识间的内在联系和发展脉络串联起来,引领学生思考探究领悟,所以教材文本中设置的问题提供给了学生学习时深入思考的时间与空间,也促进了学生的思维自然流淌。
(三)结构合理,有利创新
无论是章节安排还是正文中的知识点呈现,都遵循数学知识的内在逻辑顺序,因而结构合理,很适合学生自学,同时也有利于教师创造性地进行教学设计。
比如教材中的“探究”,其实就在暗示教师可通过类比的思想方法来引导学生。由于弧度制是用弧长与半径之比来定义的,故学生心中会有疑惑:明明是度量角的单位,却为何要用别人的长度之比来衡量呢?这是本节课的教学难点之一,而教材安排的这个“探究”,就是让弧度制的定义达到呼之欲出的地步。此时,教师可回顾化学中元素原子量的定义,这样通过类比就能比较顺畅地得出弧度制概念。显然,教师采用跨学科整合知识的教学设计是一种创新,可以很好地突破教学难点。
(四)蕴含哲理,励志育人
在教材的章节引言、小贴士或“阅读与思考”“探究与发现”栏目中,会介绍一些概念、定理、公式等数学知识的历史发展过程,包括数学家们的研究历程,这些具有人文性与哲理性的数学文化,值得教师继续深挖掘,将其背后蕴含的育人元素开发出来融入数学课堂,以落实“立德树人”的育人理念,实施学科德育。
比如,教材在得出弧度制概念后在旁边插入小贴士,内容是介绍弧度制的大致发展过程。此处教师如果能查阅文献去深入挖掘一下就可溯源弧度制,并在教学设计时融入这些数学史料。例如告诉学生,当年数学家几十年如一日就做一件事情,这能让学生强烈感受到数学家们“坚持不懈”的毅力和精神。而这些励志事迹可以感染学生,使其养成认真学习的习惯,也可引导学生树立正确的“三观”。由此可见,教材很好地做到了科学性与人文性的水乳交融,而教师在数学课堂教学中融入数学文化的同时也渗透了学科德育。
三、创造性地挖掘新教材文本的方法
针对教材的这些文本编写新特点,教师在教学中又该如何处理呢?在“弧度制”教学实践时,应结合教材文本内容作深入挖掘,并通过融入数学史料和其他学科知识对弧度制概念进行重构设计,旨在让学生尽可能地了解为何要学弧度制和弧度制定义的合理性。
(一)弧度制学习必要性的设计
先给出两个问题:(1)一张长1 米,宽2 尺的桌子面积是多少?(2)成语“半斤八两”是何意?让学生明白长度、重量都有不同单位,从而也为角有不同单位作铺垫,接着介绍“测算地球大小”的史料。
古希腊数学家埃拉托色尼一辈子做了一件很重要的事:测算出了地球半径。他在每年夏至这天正午的同一时间,利用阳光照射两口相距800 公里的枯井,测量出了圆心角的大小(如图1),从而算出了地球半径。为了得到精准的数据,埃拉托色尼需要年复一年地测量,而一年只有夏至这一天,如果遇上阴天或雨天,只能再等一年。正是由于他的坚持不懈,测算出的地球半径非常精确[5]。
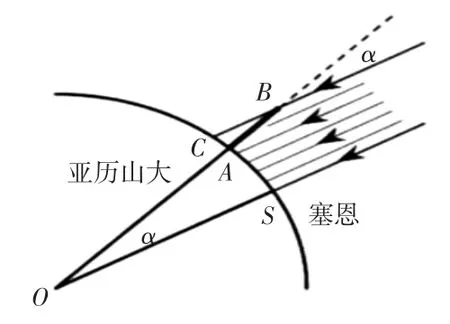
图1
接下来让学生讨论埃拉托色尼的计算原理,明白了通过地球上两地距离还需算出所对应的圆心角与弦的长度,从而理解了度量角大小的目的是为了计算圆心角所对的弧长。然后教师再例举物理学中的圆周运动,讨论线速度与角速度的关系,以进一步理解角度制的不便。
最后重回数学本身,让学生回答3 个问题:(1)sin 30°是多少?(2)若,则x是多少?(3)方程有没有解?
在回答讨论过程中令学生认识到问题(3)已不能用所学的旧知来解决了,即角度制已无能为力,因而需要一个新的度量角的单位,且最好是实数。这样的设计类比了数系扩充的方法:遇到旧知不能解决新问题,于是只能扩充新知。创设问题(3)就是让学生产生认知冲突,以了解学习角新单位制的必要性。
(二)弧度制定义合理性的设计
接着师生开始一起探究教材上的内容,让学生知道圆心角α 所对的弧长I与半径r之比只和α 的大小相关,即一旦α 确定则比值也就唯一确定,因而该比值具有客观性。同时,教师再回顾化学中元素原子量的定义方法:用质量之比来衡量,故它是个实数。于是很自然地通过类比取得共识,可以用其他的长度之比来衡量角的大小,并把这种度量角的单位制称为弧度制。
按此设计授课效果良好,学生对学习弧度制的原因能很自然地接受,而且能比较好地理解弧度制用比值来定义的道理。如果教师用简化公式(如弧长公式、扇形面积公式等具体例子)来说明学习弧度制的好处,则学生只能体会到其中一部分道理,还需要在后续学习中去进一步感受。
四、结语
新教材的文本有利于教师创造性设计。正是由于新教材的文本编写逻辑连贯、思维流畅,同时文本中又融入了数学文化,因此非常适合教师在教学设计时进行自由发挥,创造性地使用教材文本,将文本背后隐藏着的富有教育价值的内涵体现出来,从而把数学知识的“教育形态”转化为“教学形态”,互相交融,相得益彰。
新教材的文本需要教师深入挖掘与思考。新教材的文本编写详实,也设置了一些“思考”与“旁注”,但教师是否能挖掘出文本蕴涵着的意义?如果教师对所授知识点的来龙去脉不甚了解,教师自己也没有一定的数学文化储备,或者没有将“新课标”的理念执行到底,那么很可能直接忽视文本背后的涵义,从而辜负了编者的良苦用心。因此,教师首先要加强自身的专业素养,认真研讨“新课标”,坚决贯彻课标理念;其次,对教材中“问题”“思考”“旁注”等内容一定要多琢磨、多查阅文献,将其意蕴挖掘出来;最后,教师还要分析学情,再结合文本内容进行教学设计,尽量把文本所要体现的涵义设计在教学中,从数学到文化,从文化到育人,将“新课标”理念落地课堂。

