双金属AunCu0/- (n=1~9) 团簇结构、稳定性、电子及光学性能研究
韩思蕊,张慧源,郭雅雯,丁雅妮,李成刚,2,崔颍琦
(1.郑州师范学院 物理与电子工程学院,郑州 450044; 2.郑州大学 化工学院,郑州 450001)
团簇因其独特的物理化学特性,在光伏、催化及磁性材料等领域具有潜在的应用前景[1-3]。众所周知,金属团簇的性能可通过掺杂元素产生金属间化合物或者合金化加以拓展[4]。特别是金纳米团簇,金属原子掺杂可以引起原金团簇结构的重构,并产生新奇的物理和化学特性,是现代团簇科学研究的前沿热点。基于实验的光电子能谱,Koyasu等[5]测定了AunPd-(n=1~4)团簇的亲和能和垂直离解能,发现Au-Pd之间的σ键主要通过Au6s轨道和Pd5s轨道构成。利用激光沉积技术,Neukermans等[6]制备生成了过渡金属原子(Sc、Ti、V、Cr、Mn、Fe、Co和Ni)掺杂金团簇,并发现了不同掺杂团簇的幻数对应不同尺寸。理论方面,基于密度泛函理论的第一性原理计算,Zhao等[7]研究了La2Aun(n=1~9)团簇的几何结构、稳定性和电子特性,发现了掺杂提升了金团簇的稳定性,La2Au6团簇拥有相对大的稳定性,电荷从La原子转移到Au原子上,La-La键强度最大,Au-Au键强度最小等。Panjan等[8]研究了AgAunλ(λ=0, ±1;n=1~12)团簇的结构、稳定性和电子特性,发现了AgAu5、AgAu2+和AgAu2-团簇在各自体系中拥有相对强的稳定性。同时,计算得到了同实验值相符的HOMO-LUMO能隙。此外,Yarzhemsky等[9]、Li等[10]和Zhang等[11]团队分别分析了Au12M (M=Hf、Ta、W、Re、Os)、AunM2(M=Na、Mg、Al;n=1~8)和BiAun-1,0(n=2~20)团簇的结构和电子特性。发现了一些高对称性的特殊结构,和一系列新颖的电子及光学特性。总之,金属原子掺杂金团簇不仅产生了特殊的高对称结构,而且使其特性发了改变,如提高了稳定性,提升了特性(如能级结构、电离势、几何结构、电子布居等)、增强了反应活性等。
铜和金原子拥有相同的核外电子排布,铜掺杂金团簇后会产生什么新奇结构,表现出什么特殊特性呢?对铜金团簇的研究也随之展开[12-16]。基于密度泛函理论,在B3LYP泛函和Lanl2dz基组下,Wang等[12]研究了Aun和Aun-1Cu(n≤9)团簇的结构和电子特性,结果发现,n≤4时,掺杂体系的结构类似于纯金团簇;当n≥5时,掺杂体系中的Cu原子位居结构边缘处。Zhao等[13]研究了AunCum+(n+m≤6)团簇的几何结构、电荷转移特性和CO的吸附效应。当n+m≥5时,体系呈现平面和三维结构,并发现了CO易于Cu原子形成化学键的原因。随后,在B3LYP/Lanl2dz水平下,Wang等[14]研究了不同电荷(0,+1,-1)和尺寸(2≤n≤9)下纯金和铜金团簇的几何结构、相对稳定性和电子特性,发现了大多数掺杂体系在构型上同纯金结构很类似。而且,Aun-1Cu+团簇基态结构经历了二维到三维的结构突变。稳定性分析发现,Au5Cu、Au6、Au3±和Au2Cu+团簇拥有相对强的稳定性。最近,基于B3LYP/Lanl2dz水平,Guo等[15]研究了AunCu(n=1~7)结构和稳定性,发现研究体系基态拥有平面几何结构,Au5Cu团簇具有相对强的稳定性。基于DMOL3软件,Kuang等[16]对AunCu(n=1~12)团簇的结构、电子和磁学特性进行了系统分析,结果发现,掺杂体系基态相对纯金团簇有轻微的畸变,但是整体上保持平面构型。此外,随着团簇尺寸增大,热力学和化学反应特性逐渐增强。需指出的是,上述文献对于基态结构的获取均采用在已知结构基础上,通过添加、删除和替换原子后优化得到。
众所周知,合理基态结构是研究材料物理和化学特性的前提和基础,如何获取合理的基态结构是研究工作的重点。2012年,马琰铭等[17-18]研发了基于粒子群优化算法(Crystal structure Analysis by Particle Swarm Optimization,CALYSPO)的卡利普索结构预测程序。该程序通过随机变量产生的结构进行能量优化,预测出了大量团簇和晶体的合理结构[19-24]。本文基于卡里普索结构预测程序和密度泛函理论,首先,系统搜索了不同电荷下AunCu0/-(n=1~9)团簇的基态和亚稳态结构;然后,基于基态结构,研究了掺杂体系的稳定性,磁矩、极化率和化学键;最后,通过Multiwfn程序[25],拟合出了体系的光电子能谱、拉曼谱、红外谱和紫外可见光谱,并对主要特征峰进行了归属分析。
1 计算方法
基于卡利普索结构预测程序,对基态和亚稳态结构进行了系统搜索,优化过程中采用了杂化能量密度B3LYP泛函[26],对于Au和Cu原子,考虑到计算的时间和精度,选择了双ζ价电子基组合相应的Los Alamos 相对论有效核势(RECP),即Lanl2DZ基组[27]。标准的Lanl2DZ基组屏蔽了原子内层电子,可以有效降低过渡金属原子引起的双电子积分的计算难度,通常用来研究过渡金属团簇。结构优化过程中,考虑了不同的自旋多重度,并计算了团簇的振动频率,确保优化得到结构是势能面上的局域最小点,所有的计算均在Gaussian 09程序下运行[28]。值得注意的是,Wang等在文献[14]中对不同泛函(BP86,BPW91和B3LYP)下铜金团簇的不同物理量进行了对比测试,确认了B3LYP泛函对铜金双金属团簇研究的合理性。而且,该泛函的合理性也被其他研究者证实[12-13, 15]。此外,为了进一步确保基态结构的合理性,基于ORCA(Ongoing Research of Cytisinicline for Addiction)下的CCSD(T)/def2-tzvp方法[29],计算了B3LYP/Lanl2dz方法下优化的前3个亚稳态的单点能。
2 结果讨论
2.1 几何结构
基于卡利普索结构预测程序,在B3LYP/ Lanl2dz水平下优化得到了AunCu0/-(n=1~9)团簇的基态和亚稳态结构,具体结构构型见图1。其中,黄色和紫色分别表示Au和Cu原子,n(n=1~9)表示团簇的尺寸,a、b和c分别表示B3LYP/Lanl2dz水平下能量从高到低的结构。
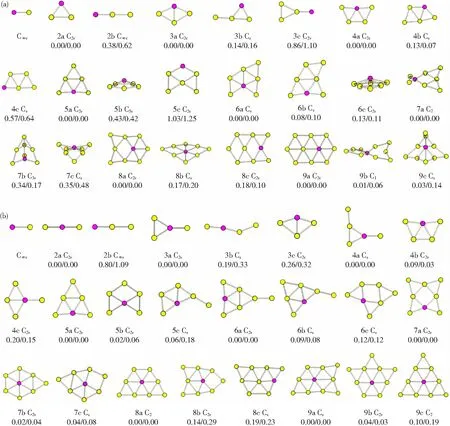
图1 (a)AunCu和(b)AunCu- (n=1~9)团簇的基态和亚稳态结构、点群对称,相对能量(B3LYP/Lanl2dz和CCSD(T)/def2-tzvp//B3LYP/Lanl2dz水平下)Fig.1 The lowest and low-lying structures of (a) AunCu and (b) AunCu-(n=1-9) clusters along with the point group symmetry and relative energy (B3LYP/Lanl2dz and CCSD(T)/def2-tzvp//B3LYP/Lanl2dz levels) (in eV), respectively
首先,对比B3LYP/Lanl2dz和CCSD(T)/def2-tzvp//B3LYP/Lanl2dz水平下的能量发现(图1),虽然两种方法下相对能量的排序有变化,但基态结构都保持着最大能量值,说明本文采用B3LYP/Lanl2dz方法优化得到的基态结构是合理的。对比结构发现,除了Au7Cu和Au8Cu-团簇的基态表现出三维结构外,其余团簇的基态均呈现二维平面结构,而且相同尺寸下不同带电体的基态结构构型也不同(n=1除外)。对比发现,AunCu0/-的基态结构可以理解为在Aun-1Cu0/-基态结构基础上添加一个Au原子得到。其次,对比前人研究结果发现,本文中Au2Cu、Au4Cu、Au5Cu和Au8Cu 的基态结构同文献[14]的结构完全相同;对于Au3Cu、Au6Cu和Au7Cu,基于本文的理论方法得到了构型和能量相同,但对称性更高的结构(文献[14]:Cs,C1,C1;本文:C2v,Cs,C2)。对比文献[15]发现,前6个团簇拥有相同的基态结构。对于Au7Cu,采用相同的理论方法,优化得到了新的结构构型,但能量上较本文的基态结构能量低0.49 eV。文献[16]中,同样发现了不同于本文的Au7Cu结构,利用本文的泛函和基组对文献[16]中Au7Cu结构进行优化,即可得到本文确定的基态结构。对于阴性团簇,Au2Cu-,Au3Cu-和Au5Cu-的基态结构同文献[14]的结构完全相同。当n=4,6时,文献[14]中的基态结构分别位居本文对应尺寸下的第二和第三亚稳态,相对基态结构的能量差分别为0.09和0.12 eV。对于Au7Cu-和Au8Cu-,采用本文理论方法优化后发现,优化后的基态结构同文献[14]中的结构和能量完全相同,但是,本文获得的结构的对称性更高(文献[14]:Cs,Cs;本文:C2v,C2)。
2.2 稳定性
为了分析团簇的稳定性,计算了平均结合能Eb、离解能Δ1E(n)和二阶差分能Δ2E(n),具体计算公式如下:
Eb(AunCu0/-)=[nE(Au)+E(Cu0/-)-
E(AunCu0/-)]/(n+1)
(1)
Δ1E(n)=E(Aun-1Cu0/-)+E(Au)-E(AunCu0/-)
(2)
Δ2E(n)=2E(AunCu0/-)-E(Aun-1Cu0/-)-
E(Aun+1Cu0/-)
(3)
式中E为不同团簇对应的能量。对于平均结合能,通常,Eb值越大,团簇越稳定。从图2(a)可以看出,随着研究团簇尺寸增大,中性和阴性团簇的稳定性逐渐增强,阴性团簇的稳定性强于中性团簇的稳定性。其次,曲线呈现奇偶变化规律,位于峰值的闭壳层结构Au3Cu、Au5Cu、Au7Cu、Au9Cu和Au2Cu-、Au4Cu-、Au6Cu-、Au8Cu-团簇拥有较强的稳定性。对比图2(a)~图2(d)发现,随着团簇尺寸增大,各曲线均呈现奇偶变化规律,而且,拥有闭壳层结构团簇稳定性较强。综上,Au5Cu和Au2Cu-团簇在各自体系中拥有相对强的稳定性。

图2 AunCu和AunCu-团簇基态结构平均结合能(a)、二阶差分能(b)、离解能(c)和HOMO-LUMO能隙(d)随尺寸变化Fig.2 Size dependence of (a) Eb(n), (b) Δ2E(n), (c) Δ1E(n) and (d) HOMO-LUMO gap energy for the lowest energy structures of AunCu and AunCu-(n=1-9) clusters
2.3 磁性分析
众所周知,根据Mulliken布居分析可以确定轨道的电子占据数,然后由自旋向上态(α)和自旋向下态(β)电子占据数之差进而确定磁矩。对于拥有闭壳层电子层结构体系,团簇的分子轨道能级中α和β的电子数目相同,一个轨道上填充2个电子,成对的α和β使用同一个轨道,即所有电子两两配对,总自旋磁矩为零,即发生了“磁矩猝灭”现象,因此,闭壳层结构团簇不具有磁性。对于开壳层电子结构体系(Au2Cu、Au4Cu、Au6Cu、Au8Cu和AuCu-、Au3Cu-、Au5Cu-、Au7Cu-、Au9Cu-),从其轨道布居发现,电子占据不同的α和β轨道。对于中性体系,α和β轨道电子占据数分别为:(29, 28)、(48, 47)、(67, 66)和(86, 85);对于阴性体系,α和β轨道电子占据数分别为:(20, 19)、(39, 38)、(58, 57)、(77, 76)和(96, 95)。对比发现,电子在α轨道上的占据数比β轨道上的占据数多一个,由于每个轨道对应一个玻尔磁子,因此,上述体系分别具有1 μB的总磁矩。此外,图3提供了开壳层体系Au和Cu原子的局域磁矩,对比发现,除了AuCu-中Au原子局域磁矩小于Cu原子局域磁矩外,其它尺寸下的Au原子局域磁矩均大于Cu原子局域磁矩。
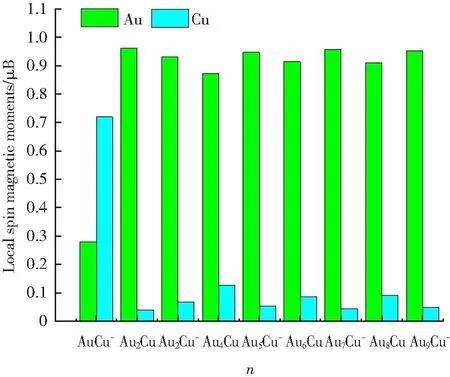
图3 开壳层体系基态中Au和Cu原子的局域磁矩Fig.3 The local spin magnetic moments of Au and Cu atoms for the lowest energy structures of opened shell systems
2.4 极化性质
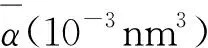
(4)
(5)
式中:αxx、αyy和αzz分别为张量对角元;N为团簇的总原子数(也称作团簇尺寸)。具体计算结果如表1所示,首先,AunCu-的平均极化率大于AunCu,说明AunCu-团簇的非线性光学效应强,容易被外加场极化。各自体系中,Au9Cu和AuCu-团簇的非线性光学效应较强,AuCu和Au4Cu-团簇的非线性光学效应较弱。其次,对于各向异性极化率,AunCu的各向异性极化率小于对应AunCu-,说明AunCu团簇对外场的各向异性响应较弱,AunCu-团簇对外场的各向异性响应较强。本文中,Au9Cu和Au9Cu-团簇对外场的各向异性响应最强,AuCu和Au3Cu-团簇对外场的各向异性响应最弱。

表1 AunCu0/- (n=1~9)团簇基态的极化率参数Table 1 The polarizability of lowest energy structures of AunCu0/- (n=1-9) clusters
2.5 适应性自然密度划分(AdNDP)
团簇的电子结构和成键模式决定了其稳定性,本节中对相同价电子结构进行了详细的 AdNDP成键分析(见图4)。其中,nc-2e代表n中心双电子键,红色和蓝色代表不同的相,ON为占据数。

图4 基于AdNDP的成键特性分析Fig.4 Bonding patterns by AdNDP analyses
对于4价电子体系,四边形结构Au3Cu中的掺杂Cu原子分别和3个Au原子形成2个对称的3c-2e σ键,占据数为1.996。线性Au2Cu-中,中心的Cu原子和两侧Au原子形成2个对称的2c-2e σ键。6价电子体系中,三角形Au5Cu中,位居底边中心的Cu原子和两侧的Au形成2个对称的3c-2e σ键,占据数均为1.996。而同一平面上所有原子形成了1个6c-2e σ键,占据数为2.000。Au4Cu-中,掺杂的Cu和4Au原子之间行成1个2c-2e σ键(ON=1.971),而另一端的1Au和2Au原子之间行成1个2c-2e σ键(ON=1.962),最后顶端的1Au、3Au和Cu原子间行成1个3c-2e σ键(ON=1.970)。对于拥有8个价电子体系的Au7Cu和Au6Cu-,Au7Cu中掺杂Cu原子和周围Au原子形成了两个2c-2e σ键(ON=1.963),此外还有2个5c-2e的σ键,对应的占据数为1.988。Au6Cu-中,三角形顶端Au和三角形外Au之间构成1个2c-2e的σ键(ON=1.974),其次,底边中心的Cu分别和周围的Au原子形成两个对称的3c-2e σ键(ON=1.964)。最后,所有原子共建了1个7c-2e σ键(ON=2.000)。对于10个价电子体系(Au9Cu和Au8Cu-),Au9Cu中的3Au、4Au、5Au、6Au及Cu原子和周围的Au原子,分别形成了3个3c-2e σ键,对应的占据数分别为1.920和1.998。最后,还包含一个占据数为2.000的10c-2e σ键。Au8Cu-中,以掺杂Cu原子为中心,同四个角分别构成了4个3c-2e σ键,相应的占据数为1.911和1.940,最后还包含一个占据数为2.000的9c-2e σ键。综上所述,铜金团簇中,众多σ键连通了整个分子骨架,促进了整个团簇的稳定。
2.6 光电子能谱(PES)
光电子能谱(Photoelectron Spectroscopy,PES)是实验上表征阴离子团簇的一种方法,能看作阴离子纳米团簇的电子指纹[30]。本节中,基于Multiwfn软件,对阴性AunCu-(n=1~9)体系的光电子能谱进行了理论模拟(图5),图中所有的峰均采用0.2 eV高斯半宽进行模拟,希望拟合出的光电子能谱能为以后的实验表征提供一定的理论依据。
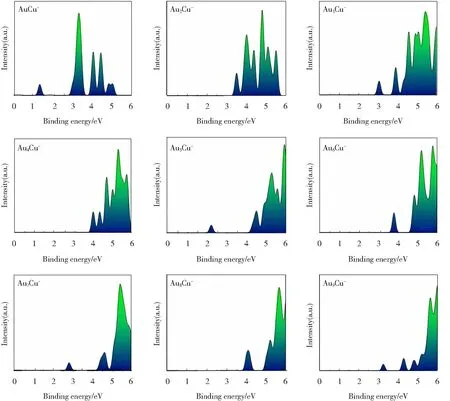
图5 拟合AunCu-(n=1~9)团簇基态光电子能谱Fig.5 Simulated PES of the lowest energy structure of AunCu-(n=1-9) clusters
2.7 红外(IR)和拉曼(Raman)光谱
本节中,基于体系的基态结构,拟合出了AunCu0/-(n=1~9)团簇基态结构的IR谱(绿色)和Raman谱(玫红色)(图6)。其中,IR谱和Raman谱的纵坐标代表相对强度。对于所有研究对象,主要特征峰集中在0~300 cm-1之间,阴性团簇对应的IR和Raman谱的振动峰较多,而且,IR和Raman最强振动峰对应的频率随着团簇尺寸的增大逐渐向低频方向转移,即随着团簇尺寸的增大,最强振动峰对应的频率发生了蓝移。

图6 AunCu0/-(n=1~9) 基态的拟合红外(绿色)和拉曼(玫红色)光谱Fig.6 Simulated IR (green) and Raman (rose) spectra of the lowest energy structures of AunCu0/-(n=1-9) clusters
中性体系中,AuCu拥有的振动模式为1(SG),IR和Raman谱具有相同最强振动峰频率(229.44 cm-1),两者均有一个振动峰,表现为Cu和Au之间沿Z轴的往复振动;类似AuCu,Au2Cu团簇拥有的振动模式为3(1A1+2B2),IR和Raman谱最强振动峰均增大到两个,对应相同的频率209.49 cm-1,表现为YOZ平面内所有原子的呼吸振动模式;当n=3,对应的振动模式为6(3A1+B1+2B2),IR谱最强振动峰频率为174.31 cm-1,表现为YOZ平面内3Au和4Cu原子的摇摆振动,Raman谱最强振动峰的频率为201.53 cm-1,表现为YOZ平面内所有原子的呼吸振动;Au4Cu拥有的振动模式为9(4A1+ A2+B1+3B2),频率为223.22 cm-1处的IR谱最强振动峰对应YOZ平面内1Au、2Cu和5Au原子沿底边的左右往复运动,低频为89.84 cm-1处的Raman谱最强振动峰对应YOZ平面内所有Cu和Au原子的呼吸振动;Au5Cu团簇的振动模式为12(5A1+ A2+2B1+4B2),IR谱最强振动峰的频率(226.01 cm-1)表现为YOZ平面内三角形底边的2Au、4Cu和6Au原子的左右摇摆振动,Raman谱最强振动峰的频率为109.67 cm-1,表现为YOZ平面内所有原子的呼吸振动;当n=6,对应的振动模式为15(11A’+4A”),IR谱最强振动峰的频率(222.78 cm-1)为XOY平面内7Cu原子在1Au、2Au、4Au、5Au、6Au五边形中往复振动,而剩余的3Au原子几乎静止不动,Raman谱最强振动峰(104.51 cm-1)表现为所有原子的呼吸振动;Au7Cu拥有的振动模式为18(9A+9B),IR谱最强振动峰位于频率170.13 cm-1处,对应于4Au和5Au,1Au和6Au沿着键的伸缩振动,频率为105.55 cm-1处的Raman谱最强振动峰对应于所有原子的呼吸振动;当n=8,拥有的振动模式为21(8A1+2A2+4B1+7B2),IR谱最强振动峰对应的频率为158.32 cm-1,表现为YOZ平面内6Au和9Cu原子沿Z轴和两侧3Au、4Au、2Au和1Au、5Au、8Au原子共同的往复振动,Raman谱最强振动峰的频率为103.6 cm-1,不同于IR谱的振动模式,6Au和9Cu原子几乎静止不动,而7Au和3Au、4Au、2Au和1Au、5Au、8Au原子共同伸缩振动;Au9Cu的振动模式为24(9A1+2A2+5B1+8B2),所有原子位居YOZ平面内,IR谱最强振动峰的频率为164.93 cm-1,表现为六边形3Au、5Au、6Au、7Au、8Au、10Cu和中心的4Au在平面内沿着垂直于Y轴方向往复振动,Raman谱最强振动峰的频率为102.94 cm-1,对应于9Au和10Cu沿Z轴往复振动。
对于阴性体系,当n=1时,振动模式为1(SG),频率166.73 cm-1处对应于红外和拉曼谱相同的最强振动峰,二者具有相同峰数,表现为Au和Cu原子之间的伸缩振动;Au2Cu-的振动模式为4(2PIU+1SGG+1SGU),IR谱最强振动峰频率为247.57 cm-1,表现为一个Cu在两个Au之间沿Z轴的往复振动,而两个Au原子几乎静止不动,Raman谱最强振动峰的频率为94.19 cm-1,同IR谱最强振动峰振动模式不同,中间的Cu几乎不动,两侧的Au原子表现为呼吸振动;Au3Cu-的振动模式为6(3A1+1B1+2B2),IR和Raman最强振动峰拥有相同的振动频率(239.12 cm-1),对应于YOZ平面内Cu和Z轴上的Au原子之间的伸缩振动;Au4Cu-团簇拥有的振动模式为9(7A’+2A”),IR最强振动峰对应的频率为241.68 cm-1,其振动模式为XOY平面内5Cu和4Au原子之间的伸缩振动,1Au和3Au之间在5Cu的影响下轻微振动,而2Au原子静止不动,最强Raman振动峰的频率为110.14 cm-1,其振动模式为XOY平面内所有原子之间的呼吸振动;当n=5时,对应的振动模式为12(5A1+1A2+2B1+4B2),频率为141.08 cm-1处的IR最强振动峰对应的振动模式为YOZ平面内三角形两个腰上Au原子的伸缩振动,Raman最强振动峰的频率为18.43 cm-1,表现为位于YOZ平面内三角形顶端的5Au原子的摇摆振动;Au6Cu-拥有的振动模式为15(6A1+1A2+3B1+5B2),IR最强振动峰对应的频率为127.64 cm-1,其振动模式为所有Au在YOZ平面内的伸缩振动,而掺杂的Cu几乎保持静止,Raman最强振动峰的频率较IR最强振动峰的频率低(92.76 cm-1),振动模式为沿Z轴的2Au和5Au原子小幅伸缩振动;Au7Cu-团簇的振动模式为18(7A1+2A2+3B1+6B2),IR和Raman最强振动峰对应的频率分别为153.16和61.37 cm-1,类似于Au6Cu-中最强峰的振动模式,分别对应于YOZ平面内的1Au,4Au,6Au和7Au原子的伸缩振动和所有原子的摇摆振动;当n=8时,对应的振动模式为21(11A+10B),IR和Raman最强振动峰分别位于162.32和100.81 cm-1处,IR最强振动峰表现为YOZ平面内梯形两个腰上的1Au、2Au、3Au和5Au、7Au、8Au原子沿相反方向的往复振动,Raman最强振动峰对应YOZ平面内梯形两个腰上的1Au、2Au、3Au和5Au、7Au、8Au原子振动方向相同的往复振动;Au9Cu-团簇拥有的振动模式为24(11A’+13A”),IR最强振动峰对应的频率为105.26 cm-1,其振动模式为XOY平面内所有原子的摇摆振动,Raman最强振动峰的频率为94.84 cm-1,表现为所有原子的呼吸振动模式。
总之,阴性团簇对应的IR和Raman谱的振动峰较多。随着团簇尺寸增大,IR和Raman最强振动峰对应的频率发生了蓝移。此外,红外和拉曼谱最强振动峰多表现为呼吸振动模式。
2.8 紫外可见光谱(UV-Vis)
采用含时的密度泛函理论(TD-DFT)和Multiwfn软件,拟合出了AunCu0/-(n=1~9)体系(前36个激发态的激发能E、波长λ和振子强度f)的紫外-可见(UV-Vis)光谱(图7)。表2给出了部分激发态的参数。首先,表2发现AuCu、Au2Cu、Au5Cu和Au2Cu-、Au6Cu-团簇振子强度最大激发态波长位于紫外光波段,其余尺寸团簇振子强度最大激发态波长位于可见光波段,预示这些体系可能具有很好的可见光活性以及潜在的可见光催化性能(图7提供了最强峰对应的频率)。
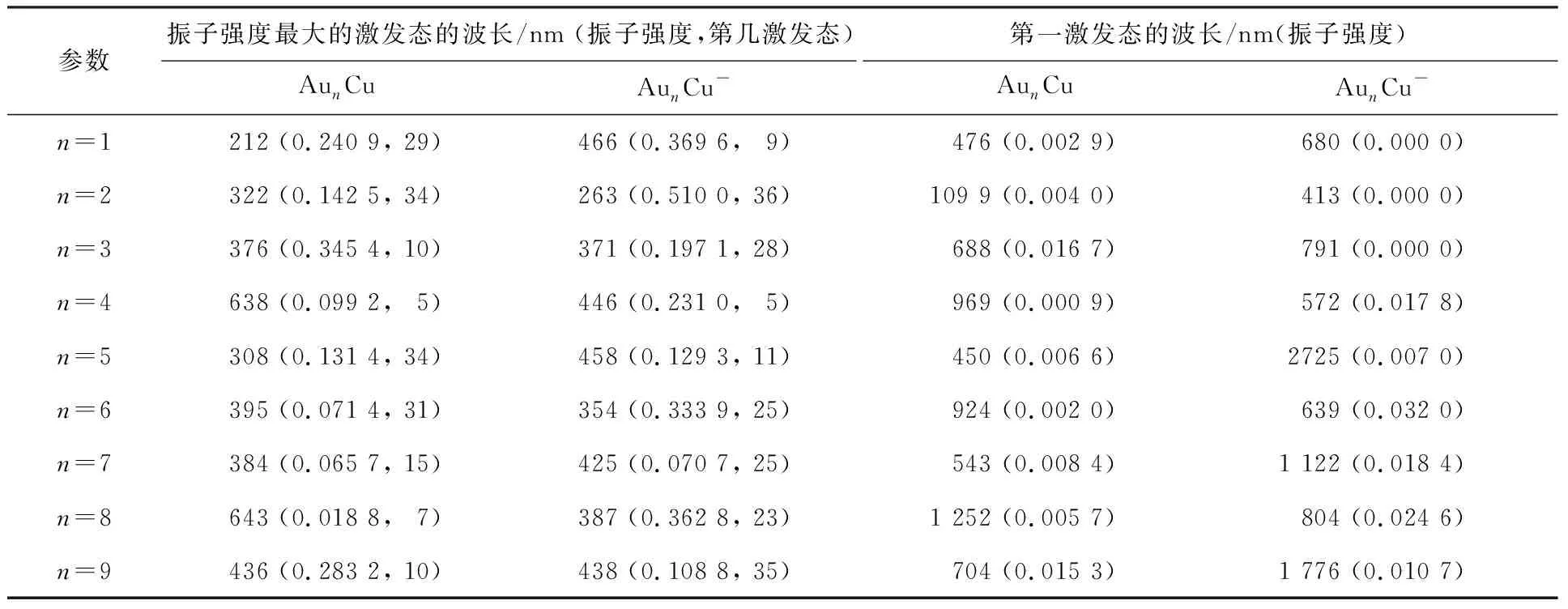
表2 AunCu0/- (n=1~9)团簇基态结构的激发特性Table 2 The excitation properties of the lowest energy structures of AunCu0/- (n=1-9) clusters
需要注意的是,因为最强吸收峰并不仅仅来源于振子强度最大的激发态,因此,图7中最强吸收峰只是大致位于振子强度最大的激发态的波长位置。其次,所有开壳层体系第一激发态均位于可见光波段,其中AuCu-、Au2Cu-、Au3Cu-团簇的第一激发态为禁阻(振子强度为0)的激发态。此外,AunCu比AunCu-体系吸收峰的强度弱,Au4Cu和Au8Cu-团簇拥有最弱吸收峰,AuCu和Au2Cu-团簇在212和263 nm处分别拥有各自体系最强吸收峰。最后,AunCu0/-(n=1~9)团簇最高峰的摩尔吸收系数随Au原子数增大呈现奇偶变化规律。
3 结 论
本文采用密度泛函理论结合卡里普索结构搜索程序研究了AunCu0/-(n=1~9)团簇的结构、稳定性、电子和光学特性,结论如下。
1) 在B3LYP/Lanl2dz水平下优化得到了不同尺寸的基态结构。结果发现,除Au7Cu和Au8Cu-呈现三维结构外,其它尺寸下的基态均呈现二维平面结构。而且,AunCu0/-的基态可通过在Aun-1Cu0/-基态基础上添加一个Au原子得到。
2) 通过计算平均结合能、离解能、二阶差分能和HOMO-LUMO能隙,确定了Au5Cu和Au2Cu-团簇在各自体系中拥有相对强的稳定性。
3) 闭壳层电子结构体系(AuCu、Au3Cu、Au5Cu、Au7Cu、Au9Cu和Au2Cu-、Au4Cu-、Au6Cu-、Au8Cu-)的总自旋磁矩为零。开壳层电子结构体系(Au2Cu、Au4Cu、Au6Cu、Au8Cu和AuCu-、Au3Cu-、Au5Cu-、Au7Cu-、Au9Cu-)分别具有1 μB的总磁矩。
4) 极化率分析发现,AunCu-团簇的非线性光学效应强,容易被外加场极化。Au9Cu和Au9Cu-团簇对外场的各向异性响应最强,AuCu和Au3Cu-团簇对外场的各向异性响应最弱。
5) AdNDP分析发现,众多σ键连通了整个分子骨架,促进了整个团簇的稳定。
6)拟合出了体系的光电子能谱,红外、拉曼和紫外可见光谱。阴性团簇中IR和Raman谱的振动峰较多,随着团簇尺寸增大,IR和Raman最强振动峰对应的频率发生了蓝移。此外,红外和拉曼谱最强振动峰多对应于呼吸振动模式。AunCu(n=3, 6, 7, 8, 9)和AunCu-(n=1, 3, 4, 5, 7, 9)团簇具有很好的可见光活性以及潜在的可见光催化性能。希望不同光谱的特征峰可为以后的实验和理论研究提供参考。

