气动载荷对高速列车车体强度的影响研究

冯 振,李明理,张璟鑫

(中车青岛四方机车车辆股份有限公司 技术中心,山东 青岛 266111)

列车在高速运行时,会带动列车周围的空气随之运动,形成一种特定的非定常流场,通常称之为“列车风”[1]。列车风致使列车附近环境空气压力波动,并引起强烈的空气流动。两列高速运行的列车会车时,在交会的瞬间,空气扰动会猛烈加剧,形成一种瞬态压力冲击波,尤其是在列车的头部或尾部交会时,会引起该列车交会侧侧墙表面的压力突变[2],即在约几十秒内出现正负压力波动,该压力波动可能会导致车厢产生较大变形、列车瞬态横摆过大等,严重影响行车安全和乘客乘坐舒适性[3-4]。我国对这一空气动力学问题相当重视,将列车会车过程中压力波动的考核定为列车运行安全评估的重要项点之一,并在高速列车的研发过程中将压力波动幅值作为车体外形设计的主要考量指标。随着列车运行速度的提高,高速列车气动载荷对车体结构强度的影响越来越显著,但其是否达到我们所关心的比率,是必须研究的问题。目前国内研究仅限于研究会车过程中车体压力分布和气动作用力变化,并未深入将气动载荷施加到车体上对车体进行强度评估,也未对气动载荷的加载方式有所讨论。本文以高速列车明线会车压力波动为载荷输入源,将车体特定测点瞬态压力波时间积分转化为车体侧墙表面的多工况载荷,依次加载各工况模拟整个交会过程的气动载荷,并讨论了其对车体结构强度的影响。

1 车体有限元模型建立

该车体由底架、侧墙、车顶和端墙组成,车体采用车辆全长的大型中空挤压铝合金型材焊接而成。相较于车体纵向和横向尺寸,型材板厚尺寸很小,符合薄板理论的要求,可以忽略沿厚度方向的应力变化。

本文采用有限元分析软件中的壳单元对车体进行有限元分析。参照车体的实际结构选择合适的单元尺寸,对车体局部位置进行人工网格控制,使整个模型具有较好的网格精度。遵循有限元分析精度和求解经济性相协调的原则,通过有限元网格的收敛性检查,最终确定了车体有限元模型,如图1所示,车体有限元模型共包含155 226个单元、116 021个节点。

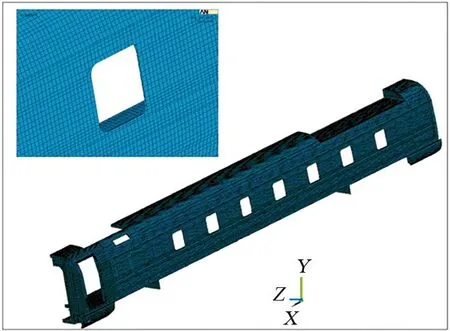
图1 车体有限元模型

2 气动载荷工况确定

2.1 车体瞬态气动载荷

高速列车交会分为明线会车和隧道会车2种情况。相较于明线会车,隧道交会的压力波动更为剧烈,隧道交会压力波动受列车运行速度、隧道长度、隧道横断面尺寸、列车交会位置距隧道出入口距离等因素影响,波形复杂多变。相比之下,明线会车压力波波形更加典型,故本文以明线会车为例,提出了一种气动载荷的加载方式,实际工程需考虑隧道会车压力波动并为之展开深入研究。

本文以高速列车明线等速会车压力波动为载荷输入源,交会侧的典型压力波[5]如图2所示。

图2 明线会车交会侧典型压力波波形图

对于非交会侧,由于高速列车在空旷地带交会,非交会侧的气动载荷波动变化很小,对车体结构强度贡献较小[6],本文不予考虑,重点考虑交会侧的压力波动。同时,根据实车试验数据和模拟仿真数据[7]可知,车体侧墙同一纵向位置处的测点压力波动幅值随测点高度的降低而增大,原因在于测点越接近地面,交会时该区域空气受扰动越剧烈;但幅值变化不大,故本文取车体同一纵向位置处压力幅值最大值代表该纵向位置的压力幅值,即模拟最恶劣的状况。此时,交会过程即可看成一条垂向压力波线纵向扫掠过车体侧墙表面。

2.2 气动载荷时间积分转化

模拟仿真数据和实车试验得到的是车体特定测点的瞬态压强,研究气动载荷对车体强度影响首先需将该瞬态压强转化为整个侧墙表面上的载荷,在此对该瞬态压强采用时间积分的方法。压力波动数据参考数值模拟分析的300 km/h等速交会数据[8],为能完整地表达列车交会过程中气动载荷对车体结构的影响,同时考虑计算机的计算能力和计算时间,取气动载荷波动较为剧烈的头波部分作为载荷输入,如图3所示。计算区域时间步长划分越精细越接近瞬态载荷作用,但同时也意味着计算量的增加。列车交会时正负压力波动约为0.18 s,综合考虑结果精确性及计算经济性,将该区域分为10个时间步长,每个时间步长间隔为0.018 s,如图4所示。

图3 应力波动计算区域

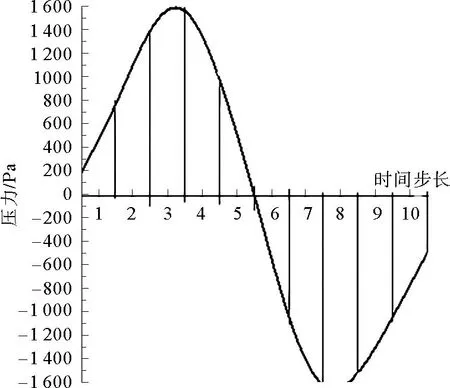
图4 计算区域时间步长图

列车以300 km/h等速交会,在每个时间步长内,该压力波扫掠过的距离为:

(1)

确定每个时间步长压力波扫掠过的距离为分区长度,该车体长24.168 m,故将车体部分划分8个分区,分区1至分区7的纵向长度为3 m,分区8的纵向长度为3.168 m,如图5所示。

图5 气动载荷车体分区图

每个时间步长压力波扫掠过的距离s对应车体上1个分区,瞬态压强与该分区平均压强关系如下式:

(2)

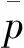
将s=vt代入式(2)得:

(3)

式中:v为列车运行速度,t为时间步长。

求得分区平均压强为 :

(4)

由式(4)可以发现,分区平均压强数值等于瞬态压力波时间积分与时间步长的比值,对10个时间步长进行时间积分,求得10个时间步长平均压强,如表1所示。

表1 压力波各时间步长平均压强 Pa

2.3 确定气动载荷工况

第一时间步长压力波到达车体分区1时记为第一工况,此时压力波刚到达车体侧表面;第十时间步长压力波到达车体分区8记为最后1个工况,此时压力波已经扫掠过整个车体侧墙。共有17个工况,每个工况下8个分区压强如表2所示,其中压强值为正表示压力垂直侧墙表面指向车体内部,压强值为负表示压力垂直侧墙表面指向车体外部。

表2 气动载荷工况列表 Pa

上述17个工况按顺序加载即代表压力波扫掠过车体侧墙的整个过程。加载时,对于车门和车窗处载荷,考虑到实际情况,根据其面积和不同工况下该分区的压强,分别计算出车门和每个车窗上承受的压力,将该压力对应加载到车体有限元模型车门边框和车窗边框上的节点上,即门窗上的力均匀分散到门框和窗框上。

3 气动载荷计算结果分析

3.1 车体“关注点”当量应力

为了研究气动载荷对车体强度的影响,增加1个垂向静载工况(不加载气动载荷,仅有垂向载荷),并在车体上选取12个“关注点”,对比气动载荷加载前后这些“关注点”当量应力的变化,“关注点”具体位置为:点1、点2分别为1位端和2位端的空气弹簧位置处;点3、点4为底架集中设备悬挂处;点5为车门上边角位置处;点6至点12分布在车窗窗角位置处。

未加载气动载荷,即在垂向静载工况下,上述“关注点”当量应力如图6所示。以气动载荷工况8为例,该工况下“关注点”当量应力如图7所示。

图6 垂向静载工况“关注点”当量应力

图7 工况8“关注点”当量应力

为了更直观地对比研究气动载荷对车体结构强度的影响,将各“关注点”在不同工况下(工况18垂向静载工况)的当量应力做成柱状图,以“关注点”5和“关注点”8为例,其各工况下当量应力柱状图如图8和图9所示。对比这2个“关注点”数据图发现,受气动载荷影响,这2个“关注点”当量应力幅值分别为10 MPa和15 MPa左右,可见气动载荷对车体强度的影响是相当显著的。

图8 “关注点”5各工况应力柱状图

图9 “关注点”8各工况应力柱状图

3.2 气动载荷强度贡献率

评估车体强度时相关文献将气动载荷与其他载荷叠加组合[9-10],未量化气动载荷对车体强度的影响。为定量研究气动载荷对车体强度的影响,在此我们定义气动载荷对车体强度贡献率δ,计算公式如下:

(5)

式中:σ为未加载气动载荷,即垂向静载工况作用下“关注点”当量应力;σmax为加载气动载荷各工况下该“关注点”最大当量应力。

通过δ值反映气动载荷对车体强度的影响,其结果数据如表3所示。由表3可知,相比于车体底架,气动载荷对侧墙影响更大,主要体现为对车体门角及窗角处强度贡献率较大,其中对于车体门角和第三车窗窗角处影响最大,强度贡献率分别达到了24.10%和37.30%。原因在于车门和车窗上的气动载荷作用到车门和车窗边框上时,受气动载荷影响大。

表3 气动载荷对车体底架“关注点”强度贡献率

4 结论

本文以某动车组车体为研究对象,参照其模拟仿真的300 km/h明线等速交会车体测点压力波数据,首次对气动载荷加载方式进行了讨论,并在车体上选择“关注点”,通过对比气动载荷加载前后“关注点”当量应力分析了计算气动载荷对车体强度的影响,主要得出以下结论:

(1) 提出了一种列车气动载荷加载方法,即将车体测点的瞬态压强通过时间积分转化为车体整个侧墙上的气动载荷,从而使瞬态过程转化为多工况来模拟会车过程中的气动载荷作用。

(2) 相比于车体底架,气动载荷对车体侧墙影响更大,主要体现为侧墙车门、车窗角及车顶设备安置处,最大强度贡献率达到了37.30%,出现在第三车窗窗角处;气动载荷对车体强度影响十分显著,在车体强度评估过程中考虑气动载荷是相当有必要的。