三峡大坝巴东地震动力响应分析与强震监测比对研究
童广勤,梁 辉,耿 峻,涂 劲,张 弛,秦维秉
(1.中国长江三峡集团有限公司流域枢纽运行管理中心,湖北 宜昌 443133;2.中国水利水电科学研究院,北京 100048)
1 研究背景
鉴于三峡水利枢纽工程建筑物安全的重要性和地震的不确定性,三峡大坝强震监测工作一直很受重视,其原因是大坝及周缘地区一旦发生破坏性地震,能够及时收集及分析地震在震动过程中是否对大坝构成破坏,为震害分析和工程抗震加固提供科学依据[1-2]。另一方面,我国的大坝抗震设计和科研近年虽然取得了一定进展,但许多问题还在探索之中,在抗震理论和动力分析方法上具有一定难度,其理论上的方法需采用实测数据来进行验证,而强震监测资料正是对抗震设计理论做出实际检验的一种较好手段,因此,利用记录的地震监测资料,进行大坝强震反应数值分析成果的分析比对研究,是非常有意义的工作。
将有限元计算的结构地震动响应结果与实测的结构地震动响应进行对比,可以对已有的理论与计算方法进行验证。Chopra[3]对比了多个重力坝、拱坝的地震监测记录与有限元计算结果。Wang等[4]将考虑了坝体-水-基岩相互作用的计算结果与瑞士Mauvoisin大坝在遭受一次小地震时的实测结构响应进行了对比。Alves等[5]对比了Pacoima大坝遭受地震的有限元计算结果与实测结构响应。上述对比研究都各自验证并改进了理论与计算方法。然而现有大坝遭受实际地震震害的记录仍然较少,此类对比研究成果也相对较少,而随着抗震理论与计算分析方法的不断发展,亟需通过实测数据的对比来验证已有方法并进行改进、完善,为大坝抗震安全分析理论和方法的合理性和可靠性提供科学依据。
本研究采用地震波动反应分析方法,将三峡大坝在2013年巴东5.1级地震的实测自由场强震记录作为输入,进行泄2#坝段的地震反应分析,将分析结果与泄2#坝段坝体不同高程的实际强震监测记录进行比对和分析,对比了采用不同阻尼比时的成果,一方面证明了考虑辐射阻尼作用的波动分析方法能够合理反映大坝的地震响应,另一方面结果也表明对于远小于设计地震水平的较小地震动输入,混凝土坝结构体系的阻尼比应取为5%以下的较小数值。
2 计算方法
在计算分析中采用非线性地震波动反应分析方法,将坝体、地基和库水的强震反应本质上作为满足体系中接触面边界约束条件的波传播问题,在时域内以显式有限元方法求解。以黏弹性人工边界反映远域地基的辐射阻尼作用,在静力荷载作用后,考虑地震波输入进行有限元时程分析[6-10]。
2.1 波动方程时域显示积分格式有限元离散后的动力学方程:
(1)
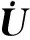
本研究采用中心差分与单边差分相结合,对速度和加速度进行如下差分:
(2)
(3)
将式(2),式(3)代入式(1)得:
MUn+1=M(2Un-Un-1)-KUndt2-C(Un-Un-1)dt+Fndt2
(4)
当质量矩阵为对角矩阵,方程具有解耦特性。由于速度采用了单边差分格式,式(4)具有一阶精度,但是由于其简单方便,且对阻尼矩阵没有限制,能够适用于有阻尼和无阻尼体系的计算,目前仍是一种经常使用的积分格式。
2.2 黏弹性人工边界有限元方法模拟无限域的波动问题中,应尽量减小底边界和侧边界的地震波反射。Lysmer and Kuhlemeyer提出黏性边界的方法来吸收反射到边界上的地震波。对于黏性边界可能引起相对较大的误差和低频失稳问题,研究人员提出了黏弹性人工边界[11-12]。在有限元方法中,底边界和侧边界设为黏弹性人工边界,底边界和侧边界的节点上施加弹簧和阻尼器,如图1所示。在数学上实现这些弹簧和减震器,可在边界相关单元矩阵的对角项上增加弹簧和阻尼项,因此将在边界节点x,y和z三方向上施加与位移和速度相关的力,相应的弹簧和阻尼系数为:
3 监测点地震动记录分析
3.1 地震情况据中国地震台网测定,2013年12月16日13时04分,在湖北省巴东县发生5.1级地震,震源深度5 km,震中位置距离三峡大坝直线距离约63 km(见图2)。
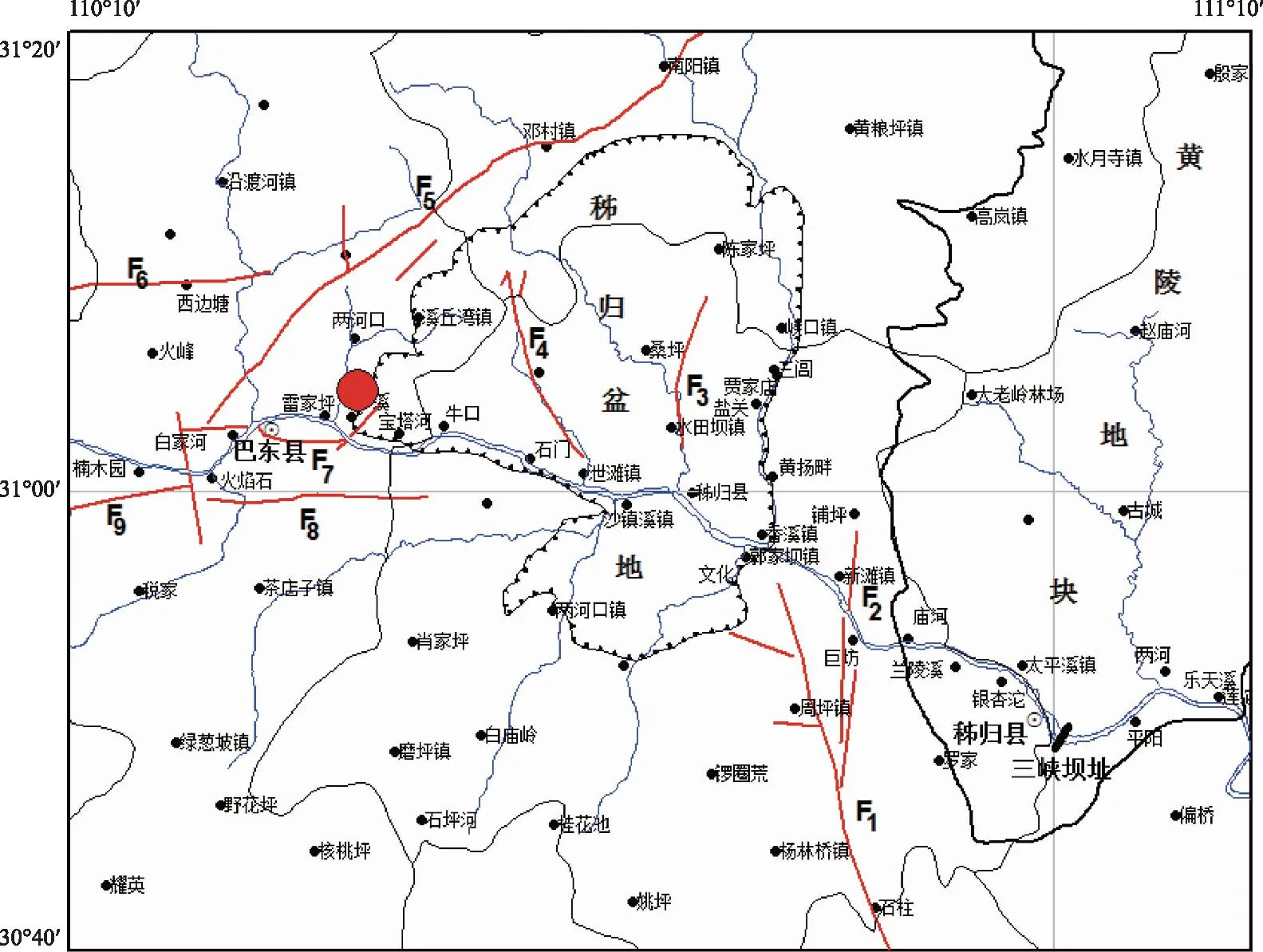
图2 湖北省恩施州巴东县5.1级地震震中位置(红色圆点表示震中位置,红色线条表示断层)Fig.2 Location of the epicenter of the 5.1 magnitude earthquake in Badong County,Enshi Prefecture,Hubei Province
3.2 强震仪测点布置为了较全面地记录在地震作用下大坝的反应特征,根据大坝结构特点,三峡大坝及副坝内安装了14套强震设备,其中泄洪2#坝段安装了5套EDAS-24IP型强震记录仪,其具体位置分别位于▽175.0 m、▽140.5 m、▽116.5 m、▽80.5m、▽15.10 m廊道中(图3所示)EDAS-24IP配置的是BBAS-2型三分向力平衡式加速度计,在左岸船闸六闸首变电站旁边处自由场测点安装了1套EDAS-24IP型强震记录仪(见图4所示)。这些拾震器的架设方位分别为铅直向及沿坝轴和垂直坝轴的水平向,仪器的技术性能能够全面反应大坝在强震作用下的反应特性,可达到了解整个坝体的反应特征。
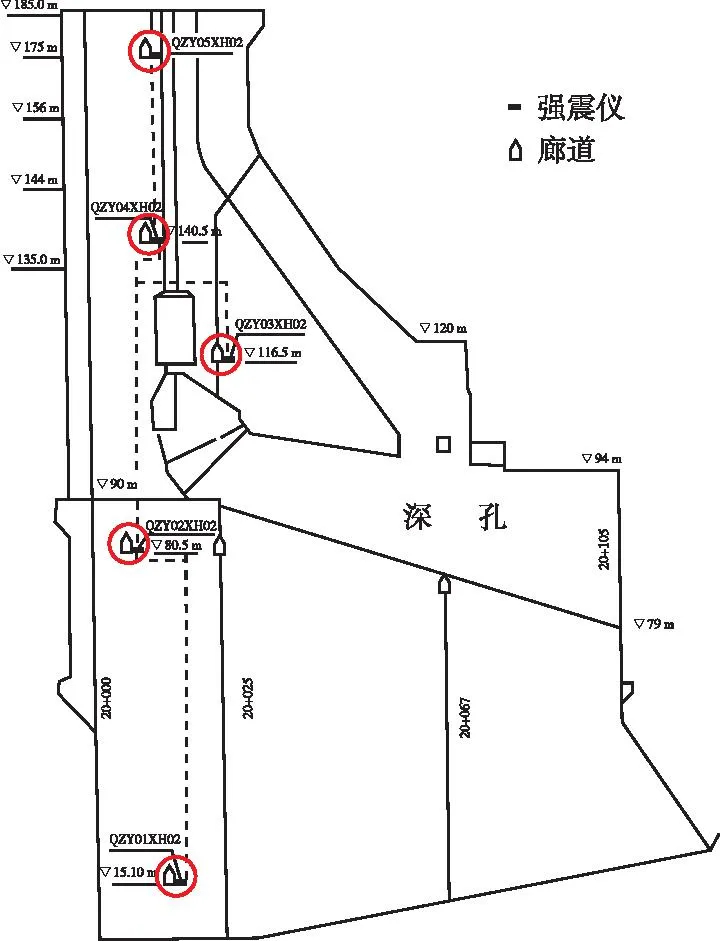
图3 大坝泄洪2#坝段5测点5套强震仪分布图Fig.3 Distribution of 5 sets of strong-motion seismograph at 5 measurement points of dam discharge section 2#
图4 船闸变电站自由场测点位置图Fig.4 Location of free-field monitoring point at the ship lock substation
3.3 监测点地震动记录分析在巴东5.1级地震中,三峡大坝14个测点中13个测点强震观测系统均获得记录,地震波形完整,震相清晰。图5给出了自由场测点滤波、校正后各方向加速度时程曲线。图6—图10给出了三峡大坝泄2#坝段各强震监测点处不同方向加速度时程曲线,表1给出了各强震监测点各方向峰值加速度统计表。由图表可知自由场测点的水平向加速度最大值是横河向,为2.04 gal。整体上,各监测点峰值加速度随高程增加逐渐增大,相对自由场测点,泄2#坝段坝顶横河向、顺河向和垂直向峰值加速度放大倍数分别为3.29、5.95和1.88。
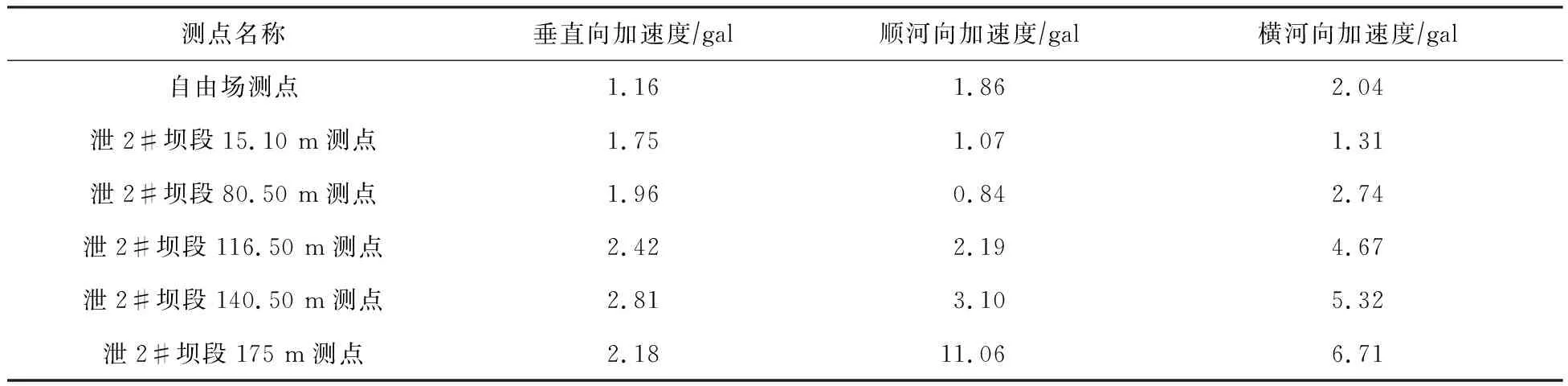
表1 巴东M5.1级强震事件三峡大坝泄2#坝段各强震监测点各方向峰值加速度统计表Table 1 Statistical table of PGA in various directions of strong earthquake monitoring points in 2# dam section of the Three Gorges Dam during the Badong M5.1 strong earthquake event
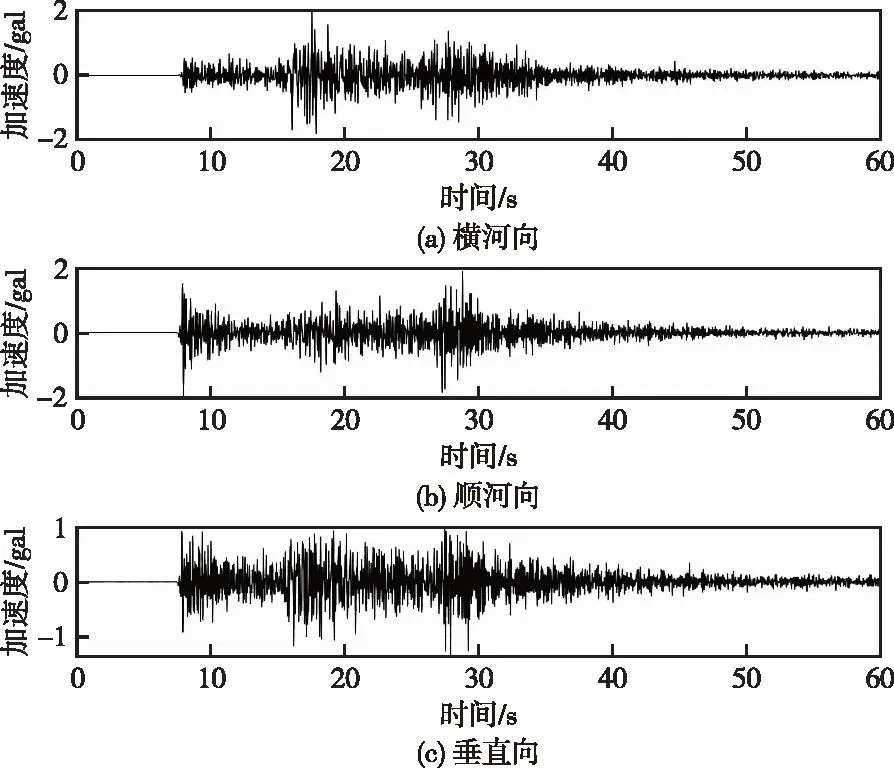
图5 自由场测点各方向加速度时程Fig.5 Acceleration time history in each direction of free field monitoring point
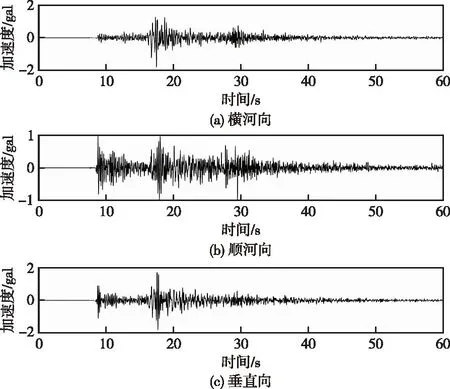
图6 高程15.1 m强震仪监测点各方向加速度时程Fig.6 Acceleration time history in each direction of free field monitoring point at elevation 15.1 m
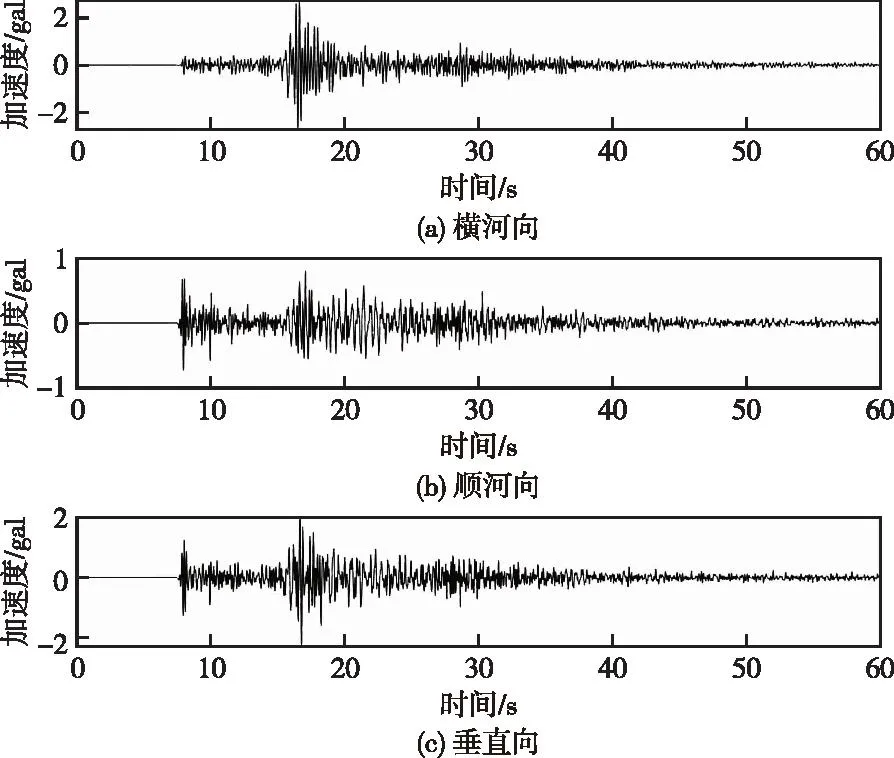
图7 高程80.5 m强震仪监测点各方向加速度时程Fig.7 Acceleration time history in each direction of free field monitoring point at elevation 80.5 m
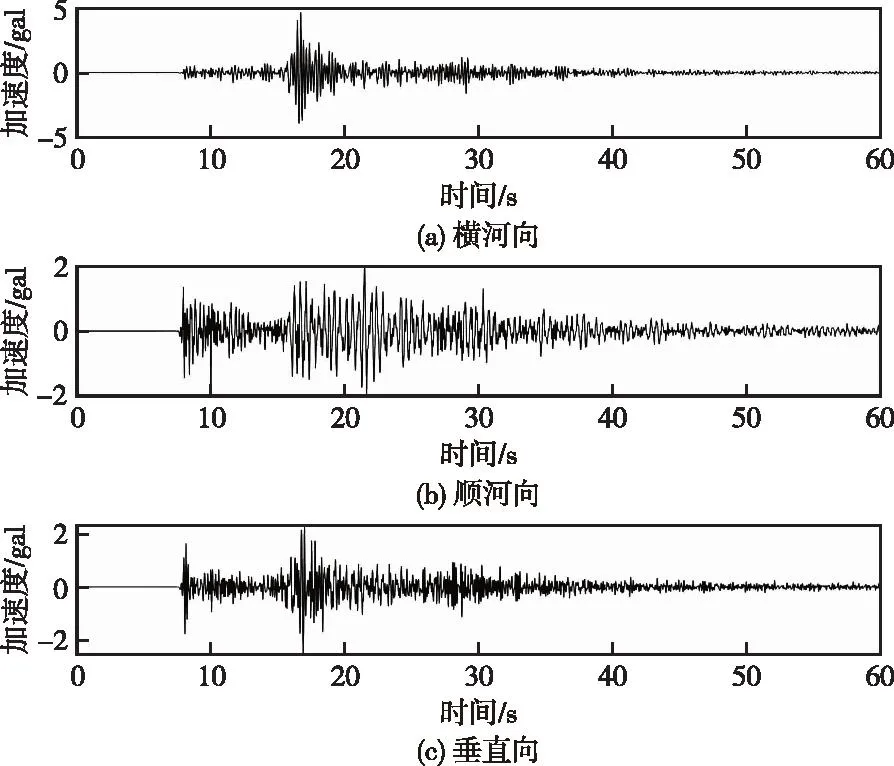
图8 高程116.5 m强震仪监测点各方向加速度时程Fig.8 Acceleration time history in each direction of free field monitoring point at elevation 116.5 m
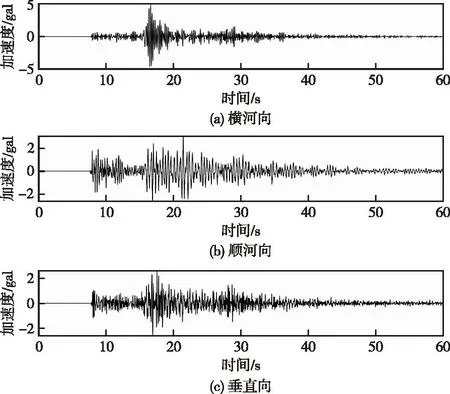
图9 高程140.5 m强震仪监测点各方向加速度时程Fig.9 Acceleration time history in each direction of free field monitoring point at elevation 140.5 m
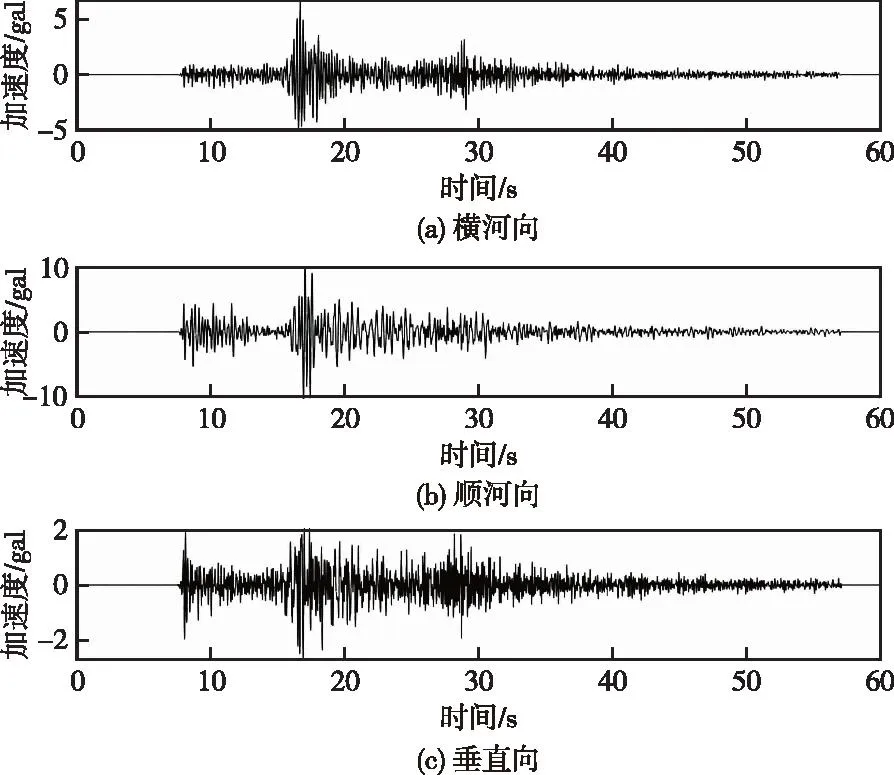
图10 高程175 m强震仪监测点各方向加速度时程Fig.10 Acceleration time history in each direction of free field monitoring point at elevation 175 m
4 三峡大坝巴东地震泄2#坝段动力响应分析与监测对比研究
4.1 计算模型和参数本文选取三峡大坝泄2#典型坝段,以实测自由场地震动记录作为输入开展抗震计算分析。图11给出了坝体-地基有限元模型,图12给出了坝体有限元模型和选取的与强震仪高程一致的监测点示意图。有限元分析模型总节点数为199 886,单元数为179 536,体系总自由度约为60万。针对坝体—库水的动力相互作用问题,经过长期研究,认为略去库水压缩性影响、以库水附加质量形式计入的方式可基本反映库水对大坝的动力影响,本研究按照现行的《水电工程水工建筑物抗震设计规范》中规定采用威斯特加德附加质量法模拟库水的影响。以图5自由场测点地震动记录作为本研究地震动荷载,采用黏弹性人工边界模拟无限地基辐射阻尼效应。综合考虑材料试验成果和设计采用值,坝体混凝土动态弹性模量取为40.74 GPa,密度取值为2400 kg/m3。三峡大坝建基于完整坚硬的微新岩体(Ⅰ类岩体)上,动态变形模量静态值为30 GPa,容重2.640 kg/m3,泊松比0.20。
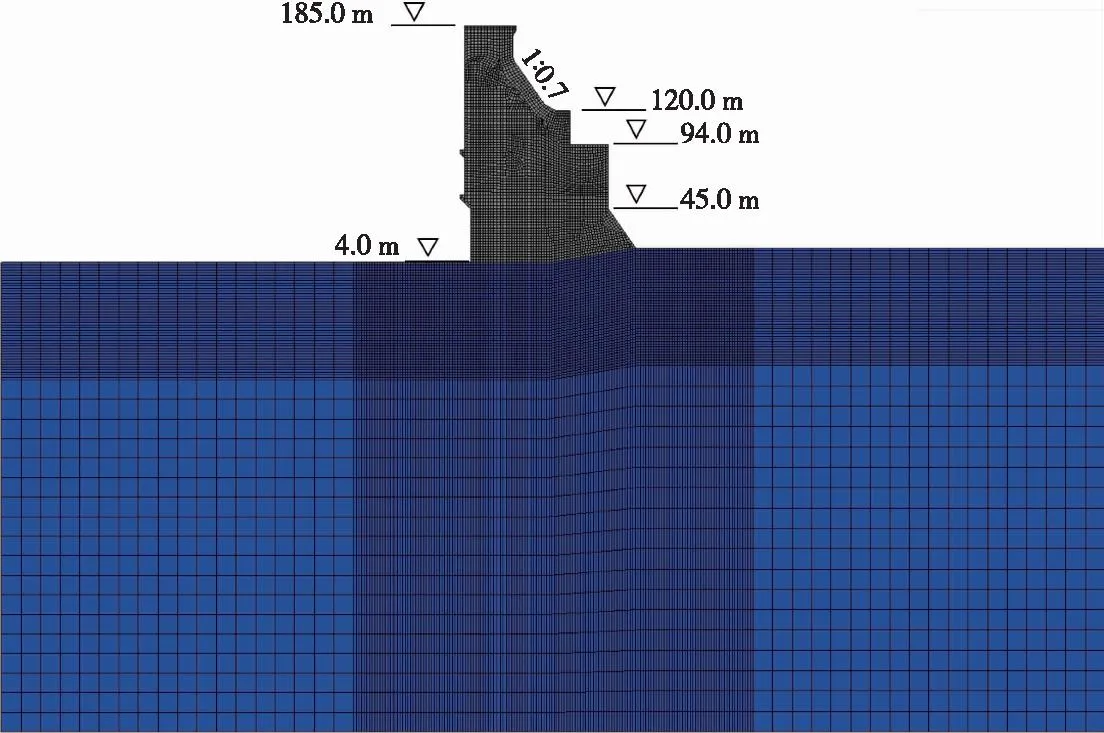
图11 坝体-地基有限元模型Fig.11 Dam-foundation finite element model

图12 坝体有限元模型和选取监测点高程示意图Fig 12 Finite element model of the dam and selected motioning point elevations
据此,本节分别考虑阻尼比按规范规定[13-14]的10%和考虑较小地震作用时阻尼比较低取2%两种情况,开展了基于巴东实测地震动记录的三峡大坝泄2#坝段地震动力响应分析,得到了与强震仪监测点相对应高程处的坝体加速度和位移响应,并与各监测点处的地震动记录加速度和位移进行了对比研究。
4.2 结果分析图13—图18给出了阻尼比为2%监测点高程15.1 m、116.5 m和175 m有限元计算顺河向和垂直向加速度与实测所得对比曲线,图19—图24给出了阻尼比为2%监测点高程15.1 m、116.5 m和175 m有限元计算顺河向和垂直向位移与实测所得对比曲线。图25—图28分别给出了阻尼比为10%时候,高程175 m处监测点和有限元计算所得加速度和位移时程对比曲线。图29—图30给出了实测、阻尼比2%和阻尼比10%计算的坝体最大顺河向、竖向加速度和位移随高程变化曲线,图 31给出了实测、阻尼比2%和阻尼比10%计算的坝体最大加速度和位移随高程变化曲线,其中最大顺河向和竖向加速度和位移均是时程绝对值最大值,最大加速度、位移分别由水平向和竖向加速度、位移时程的算数平方根最大值。
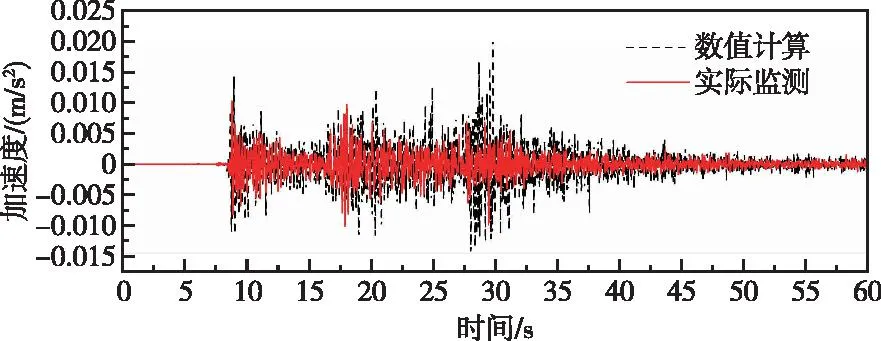
图13 高程15.1 m监测点高程有限元计算和实测顺河向加速度对比曲线(阻尼比2%)Fig.13 Comparison of stream direction PGA by finite element method and measured at elevation of 15.5 m monitoring point (damping ratio 2%)

图14 高程15.1 m监测点高程有限元计算和实测垂直向加速度对比曲线(阻尼比2%)Fig.14 Comparison of vertical direction PGA by finite element method and measured at elevation of 15.5 m monitoring point (damping ratio 2%)
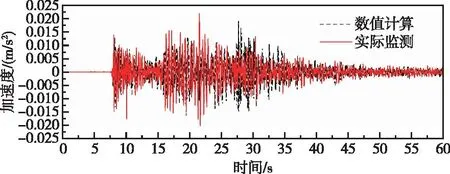
图15 高程116.5 m监测点高程有限元计算和实测顺河向加速度对比曲线(阻尼比2%)Fig.15 Comparison of stream direction PGA by finite element method and measured at elevation of 116.5 m monitoring point (damping ratio 2%)
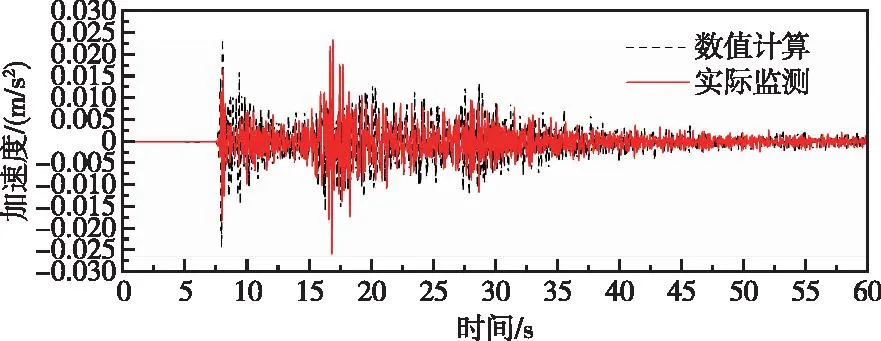
图16 高程116.5 m监测点高程有限元计算和实测垂直向加速度对比曲线(阻尼比2%)Fig.16 Comparison of vertical direction PGA by finite element method and measured at elevation of 116.5 m monitoring point (damping ratio 2%)
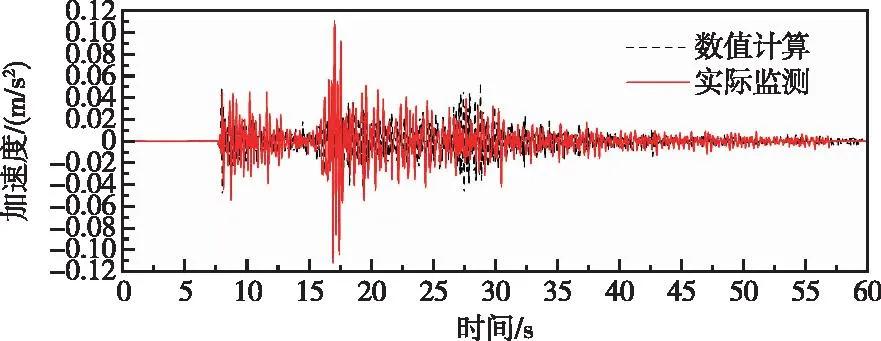
图17 高程175 m监测点高程有限元计算和实测顺河向加速度对比曲线(阻尼比2%)Fig.17 Comparison of stream direction PGA by finite element method and measured at elevation of 175 m monitoring point (damping ratio 2%)
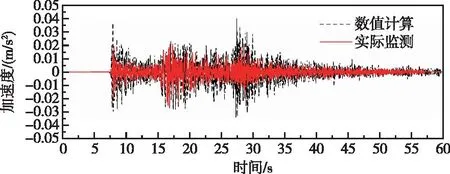
图18 高程175 m监测点高程有限元计算和实测垂直向加速度对比曲线(阻尼比2%)Fig.18 Comparison of vertical direction PGA by finite element method and measured at elevation of 175 m monitoring point (damping ratio 2%)
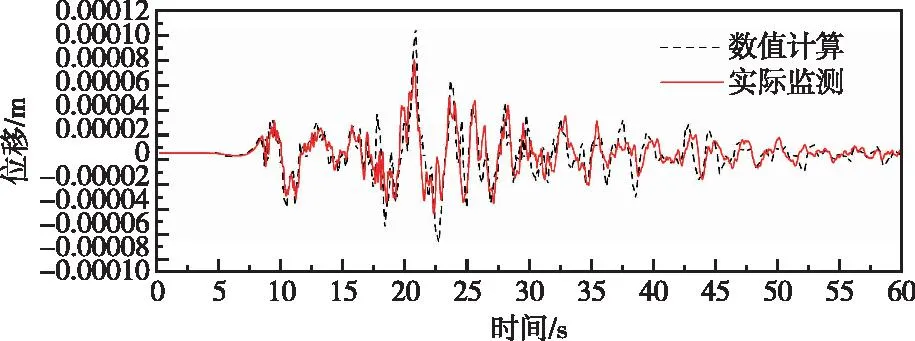
图19 高程15.5 m监测点高程有限元计算和实测顺河向位移对比曲线(阻尼比2%)Fig.19 Comparison of stream direction displacement by finite element method and measured at elevation of 15.5 m monitoring point (damping ratio 2%)
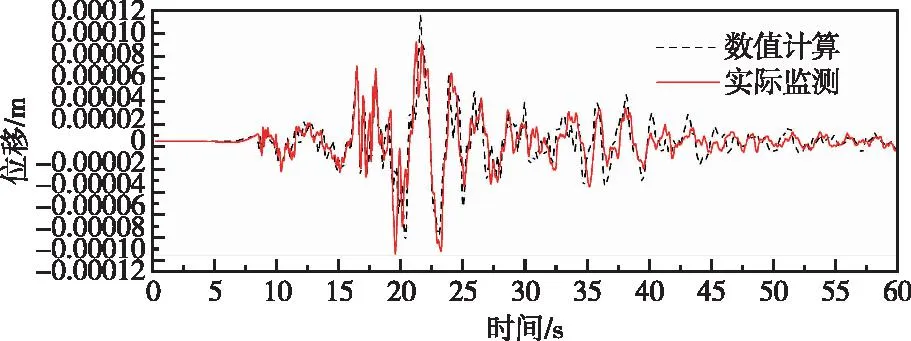
图20 高程15.5 m监测点高程有限元计算和实测垂直向位移对比曲线(阻尼比2%)Fig.20 Comparison of vertical direction displacement by finite element method and measured at elevation of 15.5 m monitoring point (damping ratio 2%)
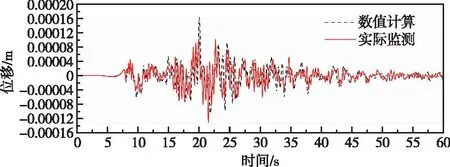
图21 高程116.5 m监测点高程有限元计算和实测顺河向位移对比曲线(阻尼比2%)Fig.21 Comparison of stream direction displacement by finite element method and measured at elevation of 116.5 m monitoring point (damping ratio 2%)
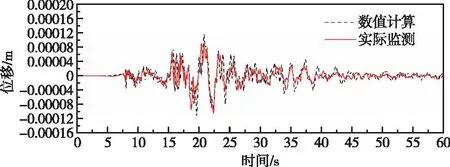
图22 高程116.5 m监测点高程有限元计算和实测垂直向位移对比曲线(阻尼比2%)Fig.22 Comparison of vertical direction displacement by finite element method and measured at elevation of 116.5 m monitoring point (damping ratio 2%)
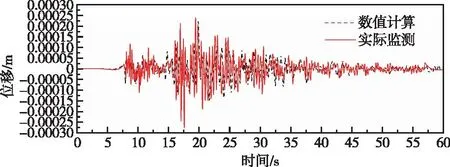
图23 高程175 m监测点高程有限元计算和实测顺河向位移对比曲线(阻尼比2%)Fig.23 Comparison of stream direction displacement by finite element method and measured at elevation of 175 m monitoring point (damping ratio 2%)
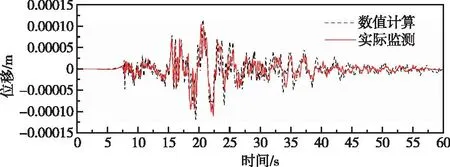
图24 高程175 m监测点高程有限元计算和实测垂直向位移对比曲线(阻尼比2%)Fig.24 Comparison of vertical direction displacement by finite element method and measured at elevation of 175 m monitoring point (damping ratio 2%)

图25 高程175 m监测点高程有限元计算和实测顺河向加速度对比曲线(阻尼比10%)Fig.25 Comparison of stream direction PGA by finite element method and measured at elevation of 175 m monitoring point (damping ratio 10%)
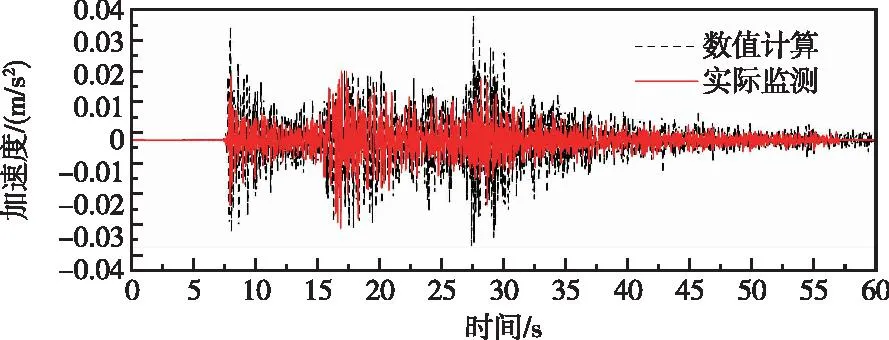
图26 高程175 m监测点高程有限元计算和实测垂直向加速度对比曲线(阻尼比10%)Fig.26 Comparison of vertical direction PGA by finite element method and measured at elevation of 175 m monitoring point (damping ratio 10%)
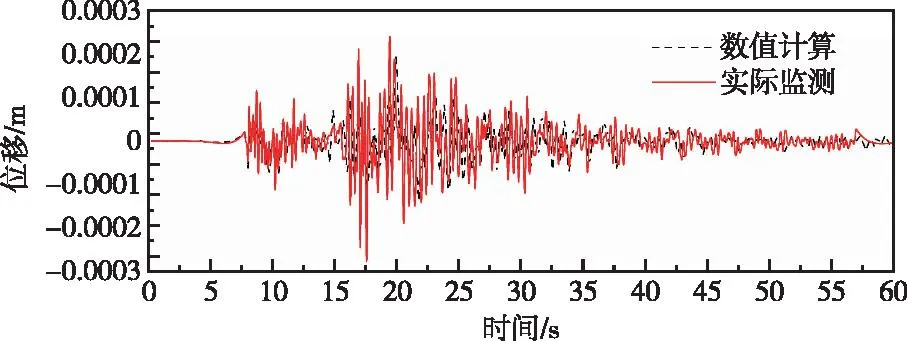
图27 高程175 m监测点高程有限元计算和实测顺河向位移对比曲线(阻尼比10%)Fig.27 Comparison of stream direction displacement by finite element method and measured at elevation of 175 m monitoring point (damping ratio 10%)
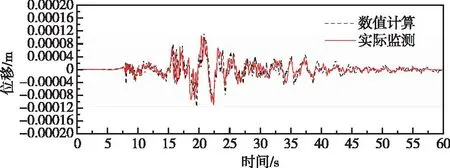
图28 高程175 m监测点高程有限元计算和实测垂直向位移对比曲线(阻尼比10%)Fig.28 Comparison of vertical direction displacement by finite element method and measured at elevation of 175 m monitoring point (damping ratio 10%)
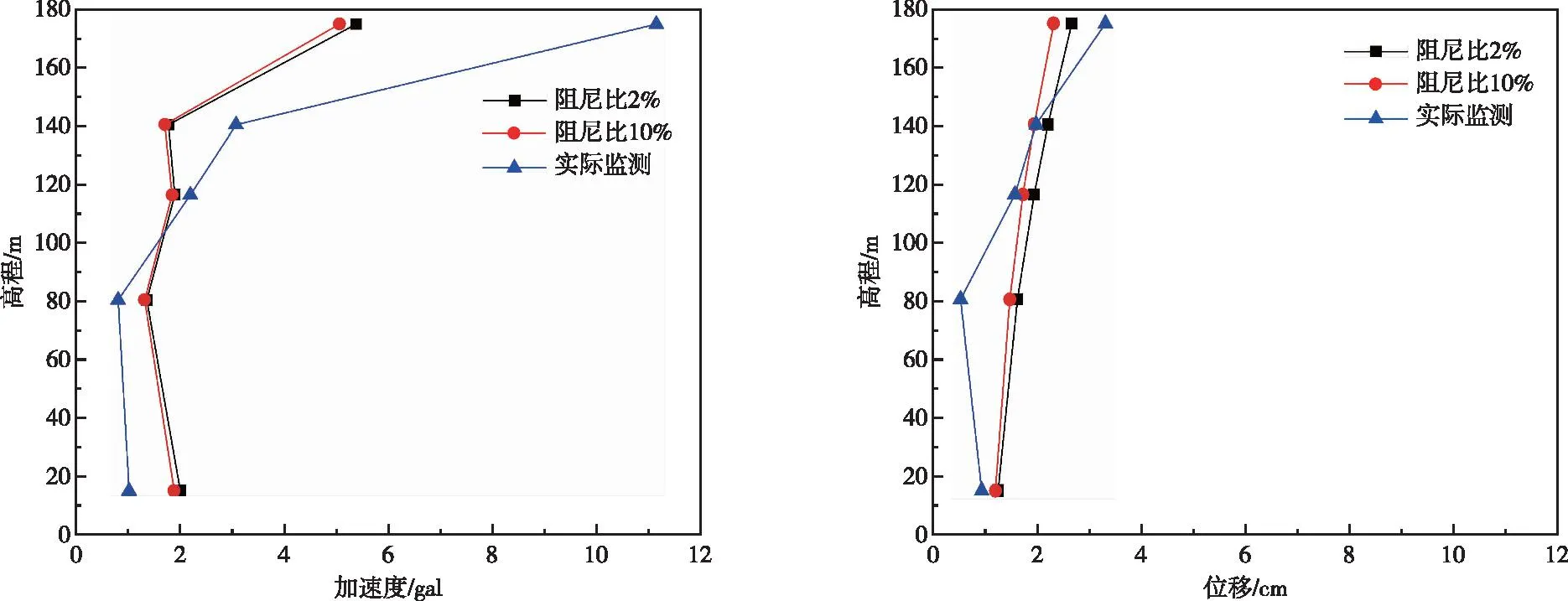
图29 实测、阻尼比2%和阻尼比10%计算的坝体最大顺河向加速度和位移随高程变化曲线Fig.29 Variation of maximum accelerations and displacements in stream river direction of the dam along with elevations obtained by actual monitoring,calculation with a damping ratio of 2% and 10%
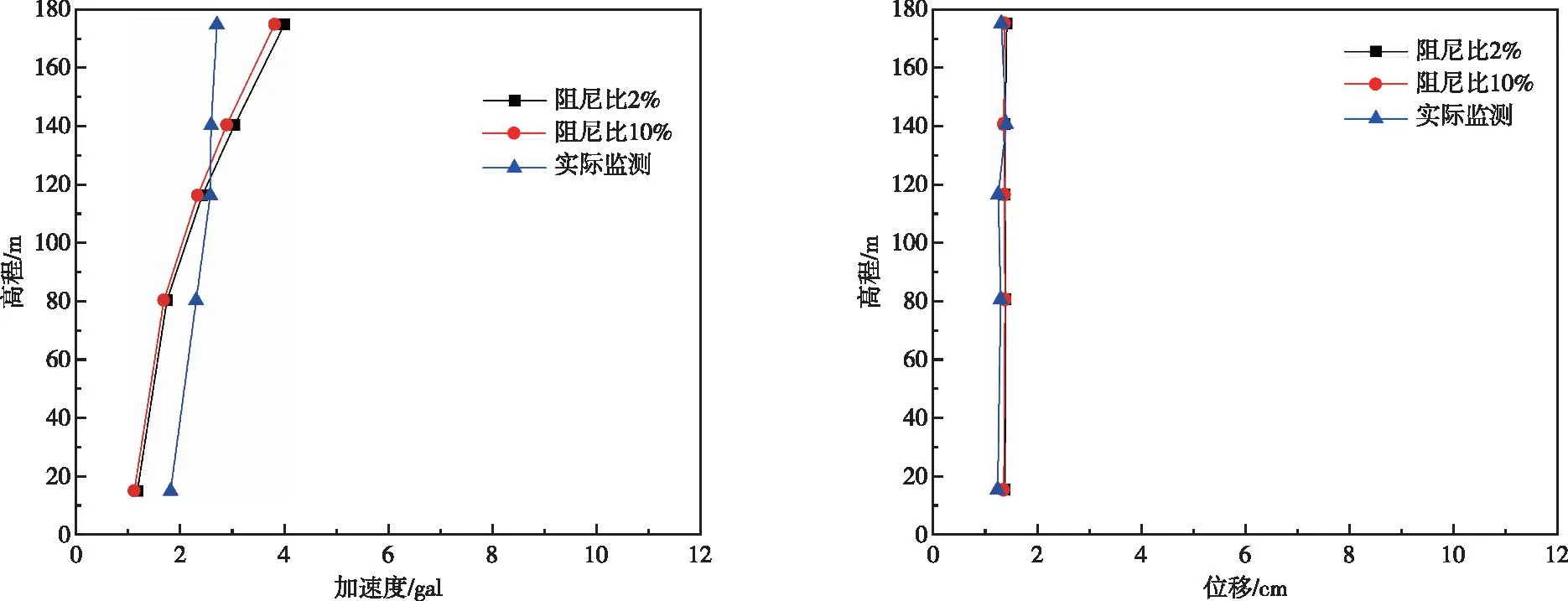
图30 实测、阻尼比2%和阻尼比10%计算的坝体最大竖向加速度和位移随高程变化曲线Fig.30 Variation of maximum vertical accelerations and displacements of the dam along with elevations obtained by actual monitoring,calculation with a damping ratio of 2% and 10%
由图13—图18可知,整体上有限元计算所得各监测点高程处加速度时程与实测值具有一定的可比性,由图29—图30在低高程位置,有限元计算所得最大顺河向加速度响应比实际监测所得最大顺河向加速度大,随着高程增加,实测值逐渐大于计算值,而有限元计算低高程最大竖向加速度大于实际监测所得值,随着高程增加计算值逐渐大于监测值。
对比实测和有限元计算所得位移时程曲线(图19—图24)可知整体上不同高程位置实测和有限元计算所得顺河向和竖向位移时程均吻合相对较好。同时由图29—图30可得,除了高程80.5 m监测点处最大顺河向位移和有限元计算所得值有一定差别,整体上各监测点记录所得最大顺河向位移与有限元计算成果相差不大,各监测点处最大竖向位移和有限元计算所得值基本一致。
由图17、图18、图23—图31可知,相对于阻尼比取2%,阻尼比取10%时,不同监测点处有限元计算加速度和位移响应均有所减小,且通过高程175 m监测点和有限元计算所得位移时程对比曲线可以发现,有限元计算所得位移响应时程整体上要小于实测值。10%阻尼比主要针对设计地震以上较强地震输入水平的情况,地震动强度较小时,如果按照《水工建筑物抗震设计标准》GB 51247—2018重力坝阻尼比取10%时,将会低估大坝地震动响应。
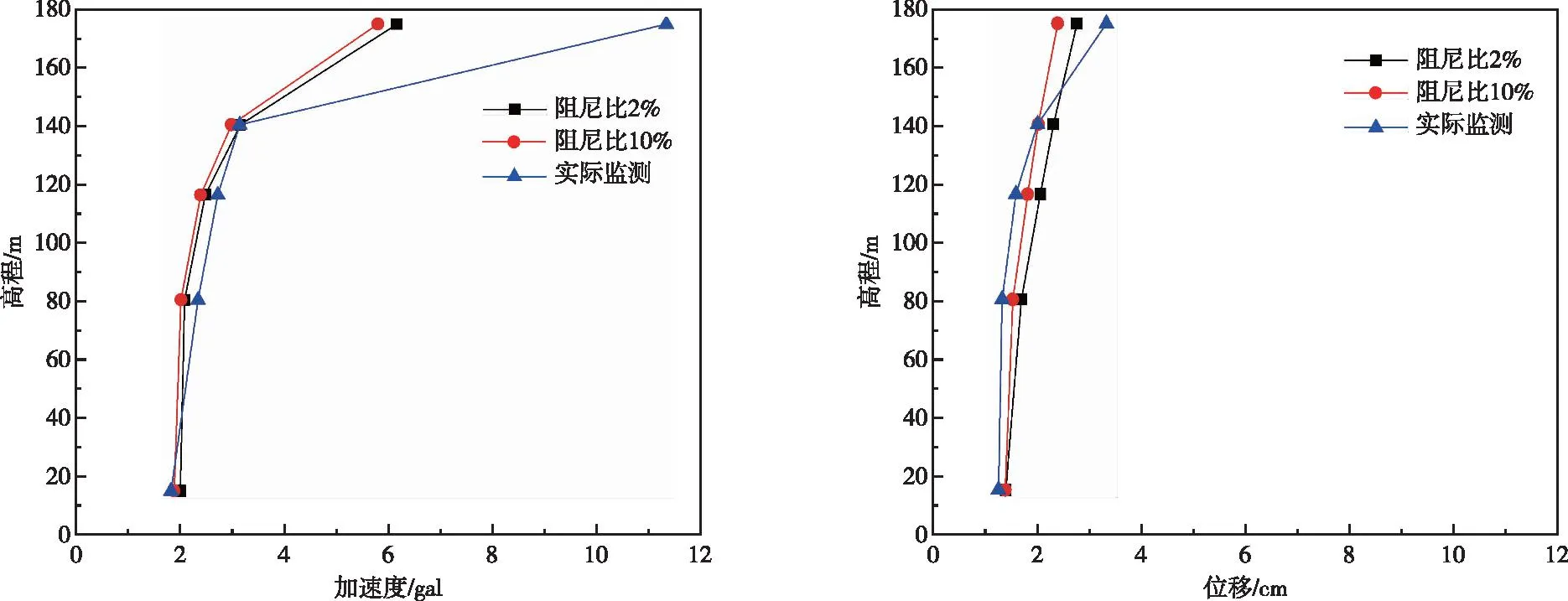
图31 实测、阻尼比2%和阻尼比10%计算的坝体最大加速度和位移随高程变化曲线Fig.31 Variation of maximum accelerations and displacements of the dam along with elevations obtained by actual monitoring,calculation with a damping ratio of 2% and 10%
5 结论
本研究以三峡大坝泄2#典型坝段为例,考虑无限地基辐射阻尼效应,采用地震波动反应分析方法,将三峡大坝在2013年巴东5.1级地震的实测自由场强震记录作为输入,考虑不同阻尼比开展了大坝地震反应分析,将有限元分析结果与泄2#坝段坝体不同高程的实际强震监测记录进行比对和分析,主要结论如下:
(1)自由场测点的水平向加速度最大值是横河向,为2.04 gal。整体上,各监测点峰值加速度随高程增加逐渐增大,相对自由场测点,泄2#坝段坝顶横河向、顺河向和垂直向峰值加速度放大倍数分别为3.29、5.95和1.88。
(2)阻尼比取2%时,整体上有限元计算所得各监测点高程处加速度响应与实测值具有一定的可比性,在低高程位置,有限元计算所得顺河向加速度响应最大值比实际监测所得顺河向加速度最大值大,随着高程增加,实测值逐渐大于计算值。除了高程80.5 m位置处有限元计算所得顺河向位移大于实测的,整体上不同高程位置实测和有限元计算所得位移时程均吻合良好。
(3)阻尼比取10%时,有限元计算加速度和位移响应均有所减小,且有限元计算所得位移响应时程要小于实测值。10%阻尼比主要针对设计地震以上较强地震输入水平的情况,地震动强度较小时,如果按照《水工建筑物抗震设计标准》(GB 51247—2018)重力坝阻尼比取10%时,将会低估大坝地震动响应。
(4)对比分析结果一方面证明了考虑辐射阻尼作用的波动分析方法能够合理反映大坝的地震响应,另一方面也表明对于远小于设计地震水平的较小地震动输入,混凝土坝结构体系的阻尼比应取为5%以下的较小数值。

