基于滑模抗扰动观测器的PMSM无差拍预测控制*

潘 登,刘义才,高 俊

(武汉商学院机电工程学院,武汉 430056)

0 引言

PMSM作为交流电机中最具代表的一类,具有结构简单、高转矩惯性比、体积小、效率高等诸多优点,在精密控制、机车牵引等领域应用前景广阔。就控制方式而言,基于PI调节器的转子磁链定向矢量控制(FOC)应用极为广泛,其关键在于定子电流幅值和空间位置的控制,分别对转速和定子交、直轴电流进行双闭环控制,系统稳态性能好。然而PI调节器的参数选择依赖于电机数学模型,由于PMSM是一个强耦合的非线性系统,电机电阻R、电感L及磁链ψf等参数变化对系统稳态性能影响较大,因此PI控制不能直接满足电机高性能、高精度控制要求。

PMSM模型预测控制的核心思想是根据逆变器和电机的数学模型,以及电机当前时刻的状态,预测未来时刻的状态,与给定值进行比较,选择出最优的电压矢量作用于电机。相对于PI调节器,模型预测控制省去了复杂的参数整定,具有更好的稳态性能[1]。与PI调节器相同,电机模型不准确或模型参数偏差会导致控制电压矢量的选取不准确,导致系统输出电流产生偏差,随着时间推移,系统累计偏差持续增大,从而恶化系统的控制性能[2]。

滑模控制作为对参数和外部干扰不敏感的强鲁棒控制,近年来一直是PMSM的研究热点。皇甫宜耿等[3]采用一种高阶滑模观测器,利用观测器输出的n阶微分实现对电机磁通和电阻的观测,但多次微分极易形成高次谐波,难以完全保证观测结果的准确性;王要强等[4]利用d轴和q轴的电流、电压偏差构建参数辨识模型,设计合适的控制率,保证观测参数的收敛性;赵法强等[5]提出一种基于快速傅里叶变换电机参数离线辨识方法,采用定子电压和电流的基波离线辨识定子d轴和q轴电感,但该方法获取的数据无法适应电机的不同工况;李旭春等[6]采用扩展卡尔曼滤波器对磁链ψf和电感L进行在线辨识,实现最小方均误差意义下的系统最优估计。

本文针对一种三电平NPC驱动的PMSM提出一种基于滑模抗扰动的预测电流控制方法(以下简称SMO+MPC方法),该方法不仅可以有效抑制电阻、电感、磁链等参数扰动给系统带来的影响;同时,相比于传统预测电流控制方法,可有效降低逆变器开关损耗,减少电机定子电流谐波分量。

1 PMSM滑模抗扰动无差拍预测电流控制系统

对PMSM做如下假设:①忽略铁心饱和,不计涡流和铁心损耗,永磁材料的电导率为零;②三相绕组对称分布,转子上没有阻尼绕组,单相绕组中的感应电动势为正弦波;③永磁体具有隐极结构(Ld=Lq=Ls)。从而得出电机定子电压、磁链方程、转矩及运动方程如式(1)～式(4)所示。

(1)

(2)

(3)

(4)

式中:ud、uq为定子电压d、q轴分量(V),id、iq为定子电流d、q轴分量(A),Rs为定子绕组相电阻(Ω),ωe为转子电角度(rad/s),ψd、ψq为d、q轴磁链分量(Wb),p=d/dt为微分算子,ψf为永磁体磁链(Wb),Te为电磁转矩(N·m),p为极对数,Tm为折算到轴端的负载扭矩(N·m),J为机械负载折算到轴端的转动惯量(kg·m2),ωm为转子机械角速度(rad/s),B为黏滞摩擦系数,B>0。

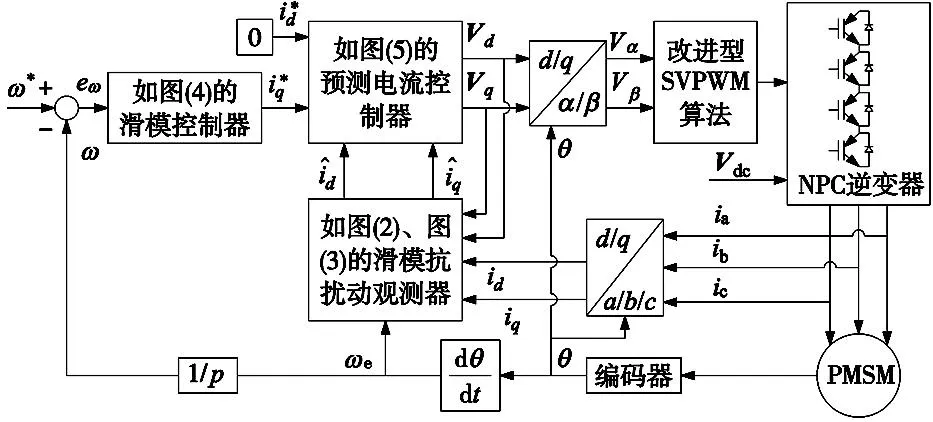
图1 滑模抗扰动无差拍预测电流控制系统结构框图

2 电流环d、q轴双滑模抗扰动观测器

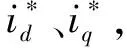
(5)

(6)

式中:fd、fq为d、q轴参数所引起的扰动,Fd、Fq为fd、fq的变化率。以id及fd为状态变量,改写式(1)成式(7)的状态空间方程:

(7)

以d轴反馈电流为观测对象,设计滑模抗扰动观测器如式(8)所示。

(8)

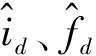
(9)

基于式(7)和式(8)得到误差方程如式(10)所示。

(10)

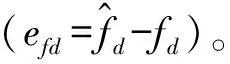
(11)

为进一步削弱由于滑模面切换而引起的高频抖振[7],使用饱和函数sat(s)取代传统的sgn(s)函数。饱和函数如式(12)所示。

(12)

式中:ρ是函数边界值,取正实数。

采用等速趋近律方式设计滑模控制函数,表达式如式(13)所示,更新式(13)得到控制率u(eid),如式(14)所示。

(13)

(14)

式中:趋近律参数ξd为正实数。

联立式(8)、式(14),可得d轴扰动值,如式(15)所示。

(15)

定义李雅普诺夫函数Vs,如式(16)所示。对该函数求导,并联立式(13)和式(14),可得式(17):

(16)

(17)

由式(17)可得,控制率u(eid)取值符合李雅普诺夫第二稳定判据,观测器大范围渐进稳定。将d轴扰动值补偿到电压方程中,改写式(5)可得式(18),对式(18)其进行离散化,最终得到d轴观测器如式(19)所示,绘制d轴滑模观测器原理框图如图2所示。

(18)

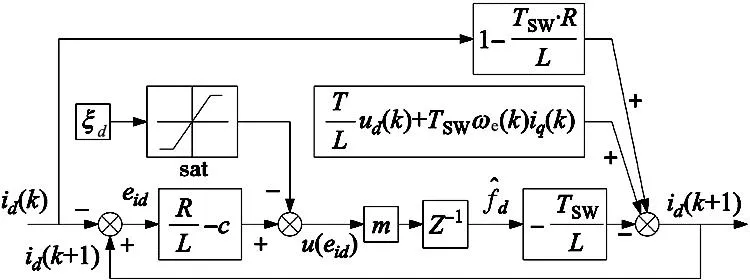
图2 d轴滑模扰动观测器原理框图

(19)

同理,以q轴反馈电流为观测对象,设计滑模抗扰动观测器如式(20)所示。其中控制率u(eiq)表达式如式(21)所示。

(20)

(21)

式中:n、c1、ξq均为正实数;q轴扰动值如式(22)所示。

(22)

将式(6)改写为式(23),并对其离散化,即得到式(24)所示的q轴观测器,绘制q轴滑模观测器原理框图,如图3所示。

(23)

图3 q轴滑模扰动观测器原理框图

(24)

3 速度外环滑模控制器

为加快系统运动点进入滑模面速度,速度外环滑模控制器基于指数趋近律法设计。定义控制器状态变量如式(25)所示。

(25)

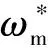
(26)

以iq作为控制率,选择线性滑模面函数,如式(27)所示。

(27)

采用指数趋近律设计滑模控制器,如式(28)、式(29)所示。

(28)

(29)

式中:ξs>0,k>0。

(30)

式(30)满足大范围渐进稳定条件,可得出指数趋近律法的滑模控制器是稳定的。将式(29)离散化,可得控制器原理框图如图4所示。

4 基于SVPWM无差拍模型预测电流控制器

4.1 模型预测电流控制器

传统PMSM模型预测电流控制方法中,采样周期Tsw内只注入单个具有最小代价函数的空间电压矢量,相电流波形和电磁转矩脉动大,加之实际系统中,采样频率受控制器硬件运行速度影响,当前计算得到的单个最优电压矢量可能在电机下一个Tsw周期才被施加,这将使系统的控制性能恶化。本节介绍一种基于注入虚拟矢量的近似两电平SVPWM无差拍模型预测电流控制算法,首先根据电机数学模型可推导下一个Tsw施加d轴、q轴参考电压矢量,进一步得出参考电压矢量所处的空间位置,再利用SVPWM控制技术,调制出三相PWM波作用于三电平NPC逆变器,最终施加到电机,实现对电磁转矩和定子磁链的追踪控制。

合并式(1)和式(2),可得到d、q坐标系下的电压方程:

(31)

在极小的采样周期Tsw内,将式(31)中d、q轴电流进行离散化得到:

(32)

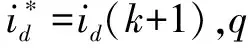
(33)

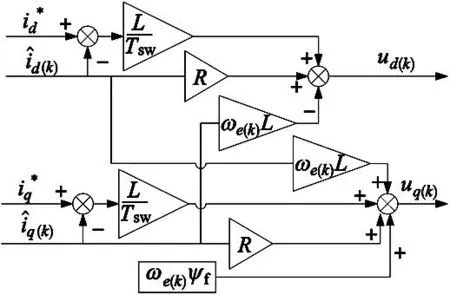
图5 预测电流控制器原理框图

(34)

4.2 改进型SVPWM调制算法

根据PMSM矢量控制的基本原理,电流预测控制器输出d、q轴的电压给定,而后通过SVPWM调制得到逆变器需要的开关信号。文献[7-11]详细介绍了传统NPC三电平SVPWM算法,算法实现流程如图6所示的①通路,显然,随着扇区划分数量的增加,矢量合成运算工作量成倍数增加。

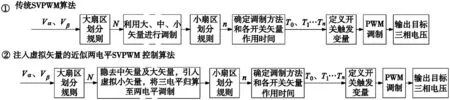
图6 SVPWM算法实现流程图

本文涉及基于注入虚拟矢量的近似两电平SVPWM控制算法,算法实现流程如图6所示的②通路。算法将电压空间矢量经过的区域划分为不对称12扇区,如图7a所示。扇区号依次为:31、32、11、12、51、52、41、42、61、62、21、22,算法隐去大矢量与中矢量,仅使用小矢量参与合成运算。定义θ角为目标电压矢量Vref与电机A相电压矢量的夹角,则有:

(35)

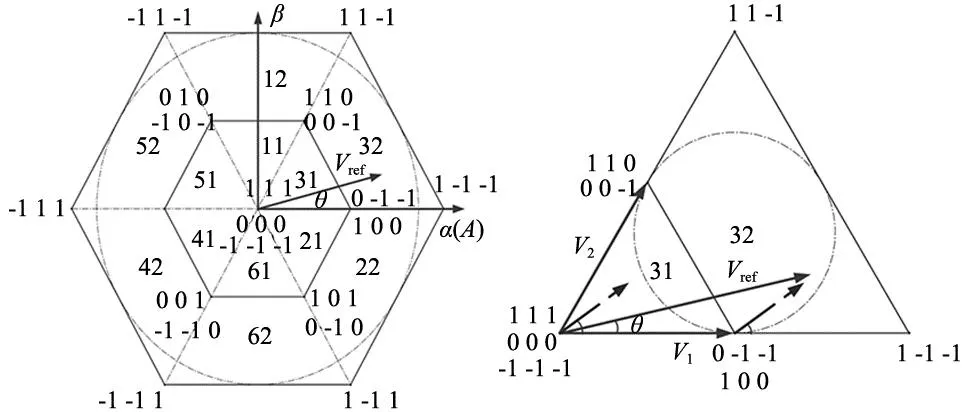
(a) 扇区分布图 (b) 电压矢量合成示意图

根据图6所示的②通路,31、32扇区内判断Vref落入对应扇区号的规则如表1所示,Vref落入其余扇区号的判断,仅需将θ角折算至31、32扇区。相较于传统36扇区SVPWM算法,12扇区运算量大幅减少。

表1 扇区判断规则表(以31、32扇区为例)

为合成一个开关周期的目标磁链,本算法采用“两电平+三电平”调制模式。如图7b所示,以31、32扇区为例,Vref落入31扇区,可按照两电平调制算法[12-13];Vref落入32扇区,通过引入虚拟矢量,可按照三电平调制算法[14-16]。根据上述规则,可依次制定各扇区基本电压矢量作用顺序及时间表[11]。

5 仿真研究

搭建MATLAB/Simulink仿真平台,PMSM参数及仿真环境如表2所示。

表2 PMSM参数及仿真环境

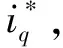
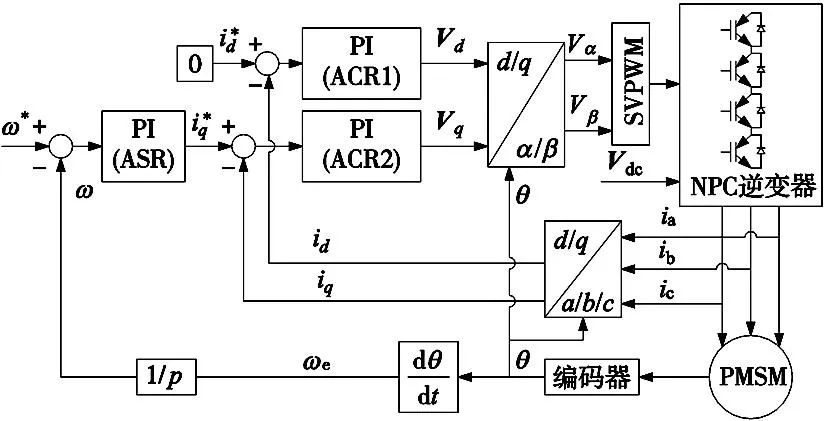
图8 基于PI调节器的传统SVPWM控制系统结构框图

分别设置系统1的PI(ASR)、PI(ACR1)及PI(ACR2)参数如下:

KpASR=0.14;KiASR=7

(36)

KpACR1=KpACR2=13.2;KiACR1=KiACR2=105.3

(37)

系统2采用SMO+MPC方法,结构框图如图1所示,实现流程如图9所示。

图9 单个采样周期内系统2工作流程图

设定仿真时间为1 s,电机给定速度为1000 r/min,电机0负载启动,在t=0.2 s时突加转矩Tm=10 N·m,图10为电机理想参数下PI控制器与SMO+MPC控制器的转矩及转速曲线图。图中负载转矩在0.2 s时加入,两种控制器下PMSM转速均下降至约950 r/min,在约0.25 s转速回升至1000 r/min。两种控制器均能迅速响应负载转矩的变化,但相比SMO+MPC控制器,PI控制器无明显抖振,转矩波形更加平稳,脉动更小。

(a) 转矩曲线(PI) (b) 转矩曲线(SMO+MPC)

以下分别针对定子电阻Rs、d轴电感Ld、q轴电感Lq及磁链ψf的不同扰动,对比分析基于两种控制器的电机转矩Te、转速n、定子电流iabc的暂态性能。

图11给出了定子电阻Rs扩大至2Rs及5Rs时,两种控制器下电机转矩及转速响应的比较结果。基于PI控制器的PMSM转矩、转速的输出纹波均大于SMO+MPC控制器。但总体来讲,定子电阻Rs的变化对控制效果的影响较低。

(a) 2Rs转矩曲线(PI) (b) 5Rs转矩曲线(PI)

图12给出了d、q轴电感Ld、Lq分别扩大至2Ld、2Lq及5Ld、5Lq时,两种控制器下电机转矩及转速响应的比较结果。图中转矩及转速输出曲线均出现不同程度的波动,但基于PI控制器的波动程度明显大于SMO+MPC控制器,且从图12d可知,当电感值扩大5倍时,基于PI控制器的转速响应曲线(n≈250 r/min)已明显小于给定值(1000 r/min),系统明显发散,转速不能恢复到设定值。总体来讲,定子电感Lx扰动比定子电阻Rs扰动对系统性能影响效果更加明显。

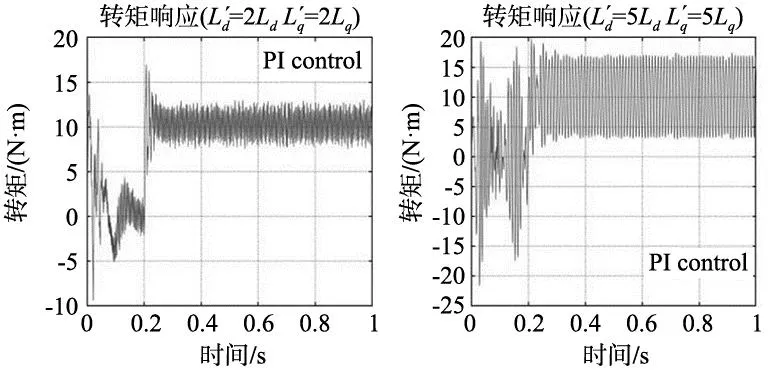
(a) 2Lx转矩曲线(PI) (b) 5Lx转矩曲线(PI)

图13给出了转子磁链ψf扩大至2ψf及5ψf时,两种控制器下电机转矩及转速响应的比较结果。基于PI控制器的电机转矩、转速的输出纹波明显大于SMO+MPC控制器,且当磁链值扩大5倍时,基于PI控制器的转速响应值(n≈480 r/min)小于给定值(1000 r/min),系统发散,转速不能恢复到设定值。总体来讲,3个电机参数对控制效果的影响从高到低可排列为Lx>ψf>Rs,即:电感失配对于系统的影响最大,其次为磁链,电阻影响最小。

(a) 2ψf转矩曲线(PI) (b) 5ψf转矩曲线(PI)

分别梳理3种不同扰动对电机理想转矩及转速曲线的影响程度,定义高、中、低、较低、极低五个等级,分别对应5、4、3、2、1五个分值。梳理上述结论,如表3所示。

表3 PMSM参数扰动对电机转矩及转速的影响程度

进一步分析电机参数改变对定子三相电流iabc暂态性能的影响,对转子磁链ψf最大失配(磁链值扩大5倍)下的A相电流进行快速傅里叶分析,如图14所示。图中在同一开关频率基准下,基于PI控制器的总谐波畸变率THD为13.98%;基于SMO+MPC控制器的总谐波畸变率THD为8.87%。后者电流波形更加平稳,脉动更小,电机的稳定性能更好。

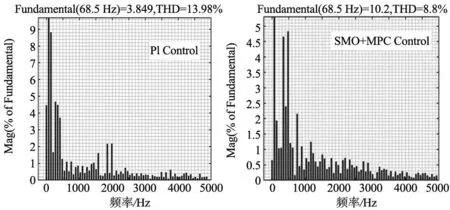
(a) 定子电流谐波(PI) (b) 定子电流谐波(SMO+MPC)

6 结论

针对PMSM电阻、电感及磁链等参数扰动引起系统控制性能下降的问题,本文提出一种NPC三电平的SMO+MPC控制方法,将滑模变结构控制技术与电流预测控制技术相结合,分别设计基于滑模控制器的转速外环、基于滑模观测器与电流预测控制器的电流内环,使系统具有较强的抗扰动能力。此外,针对电流预测控制技术存在电流波形脉动大的问题,提出一种基于注入虚拟矢量的近似两电平SVPWM无差拍控制方法,有效降低逆变器开关损耗,改善系统动态性能。通过仿真实验,验证了所提控制方法的正确性和鲁棒性。