非线性模型在储渗体预测中的应用

任 杰，侯克均，缪祥禧，樊靖宇，熊晨皓，吴晓光，章顺利，田钧名，廖哲渊，徐 兵

（1.中国石化经纬有限公司，四川成都 610100；2.中国石油西南油气田分公司开发事业部，四川成都 610066；3.中国石化勘探分公司，四成川都 610047；4.中国石化西南油气分公司勘探开发研究院，四川成都 610047；5.中国石化西南油气分公司采气一厂，四川德阳 618000；6.成都理工大学能源学院，四川成都 610059）

川中蓬莱地区处于川中古隆起的中斜平缓带的中部位置，构造地势为东南高、西北低，面积约8 500 km2，横跨遂宁市的船山区和安居区，基底稳定，褶皱平缓，总体上未见大的断裂分布[1-2]。蓬莱地区的油气勘探始于20 世纪50 年代，先后发现了侏罗系凉高山组、大安寨段油层和中三叠统雷口坡组气层。蓬莱地区上三叠统须家河组特征与川中须家河整体特征相同，广泛分布着具有良好潜力的致密砂岩天然气藏，不整合-整合于侏罗系红层之下，假整合于中三叠统雷口坡组海相碳酸盐岩侵蚀面之上，该组纵向由下到上划分为须家河组一段至须家河组六段共6 段，其中须二、须四、须六为储层[3]。蓬莱地区的开发程度已颇具规模，先后发现了蓬莱107 井、蓬莱113 井、蓬莱002-3-X1 井等高产气井，日均产气达4.95×104m3[4]。由于蓬莱地区须家河组致密砂岩储层具有低孔、低渗、非均质性较强的特点，给须家河组的勘探与研究增加了难度。

储渗体一般被定义为地层中具有一定渗透能力的孔隙与裂缝相互叠加而成的独立储集体[5-6]。总结不同地区储渗体的特征，可发现储渗体的分布大多与孔、缝、洞的发育存在直接关系。如川北柏垭地区大安寨的高能介屑滩灰岩受重结晶和溶蚀作用而变得易裂、易碎，裂缝发育，分布大量的储渗体[7]；新场气田沙溪庙组的致密气藏由于有微裂缝，所以储渗体的渗透性在纵向上变化很大[8]。

储渗体预测与储层预测基本相同，不同之处在于储渗体的预测更偏向于寻找地层中的裂缝发育带。由于储渗体大多具有非均质性,单纯在地质方面使用宏观与微观参数来对储渗体进行预测都具有片面性，所以预测方法也逐渐从早期的单一地质预测向地质、测井、地震等多学科综合预测发展，所用方法也从单一参数、经验公式等方法逐渐向多参数、跨学科新算法方向发展。测井储层预测多采用近几年流行的人工智能非线性算法，在低孔低渗的致密砂岩储层方面也取得了一定程度的突破。如宋辉等[9]运用了卷积神经网络与门控循环单元网络相结合的算法对储层孔隙度进行了预测，将两种深度学习模型结合，对于孔隙度的预测准确率高于单一的深度学习模型。

储渗体预测与常规储层预测最大的不同之处在于由于储渗体常分布在裂缝发育地区，所以需要对裂缝进行预测。国内对于裂缝预测最早可以追溯到20 世纪60 年代，虽然稍晚于国外，但也积累下来了许多适用于国内地层特征的预测方法。早期的裂缝预测方法仅限于地质方面，通过对野外露头和岩心的观测来从宏观和微观两方面对裂缝进行描述。这种预测方法仅限于有野外露头和有钻井的区域，对于未勘探地区只有进行推测，总得来说这种方法最简单，但精度非常低[10]。测井裂缝预测也随着非线性理论和方法运用的成熟，由传统的观察测井曲线对裂缝的响应发展到利用单一或多测井曲线建立与裂缝之间的线性关系来定量预测裂缝，再发展到多测井曲线建立与裂缝之间的非线性关系来预测裂缝。

国外对于裂缝的预测比国内开始得更早，PRICE[11]在分析裂缝形成过程时表示，岩石由于破裂形成裂缝，随着岩石的弹性形变增加，裂缝越多，发育程度越高。MURRAY[12]在分析构造裂缝时使用了几何学的方法计算出了曲率与裂缝孔隙度的经验公式。NELSON[13]认为由于断层而产生的裂缝与其岩性、断面的位移和距离、埋深等有关，并构建了相关函数。BARTON[14]在研究中指出，当构造裂缝的分维度大于1.34 时，此裂缝就属于具有渗流能力的裂缝网络。

20 世纪90 年代后，国外在裂缝测井识别上有较大的发展，测井识别技术方面同国内一样主要聚焦在成像测井和微波长测井上，这些方法对于裂缝和微裂缝的发育层位都有直观的识别能力。

1 工区地质特征及储集性分级评价与储渗体定义

1.1 工区地质特征

研究区位于川中蓬莱地区的蓬莱107 井区，属于川中蓬莱地区主体部分中蓬莱107 井及其附近井所在地区，面积约300 km2。研究区内共有33 口井，其中在须家河组具有中、高产能的工业气井6 口，低产及主要产水井共6 口，干井4 口。

研究区须家河组普遍发育致密砂岩，其孔隙度分布在2.0%～15.0%，平均孔隙度只有6.8%，渗透率分布在0.01～5.00 mD，已探明的须家河组天然气储量为4 162.43×108m3，已开采储量仅为110.00×108m3，剩余储量开采难度较大[15-16]。

1.2 储集性分级评价与储渗体定义

由于研究区孔隙结构复杂，孔渗相关性较差。因此，在综合考虑储层类型的前提下，将储层划分为孔隙型和裂缝-孔隙型，分别根据两类储层各自的孔渗关系（图1），在上述渗透率下限基础上，确定出两种储层的孔隙度分级评价下限。即须二段工业产能储层的孔隙度下限分别为：孔隙型储层-孔隙度大于8.0%，裂缝-孔隙型储层-孔隙度大于4.0%；中高产储层的孔隙度下限分别为：孔隙型储层-孔隙度大于14.5%，裂缝-孔隙型储层-孔隙度大于9.0%（表1）。

表1 蓬莱107 井区须二段储层分类评价标准

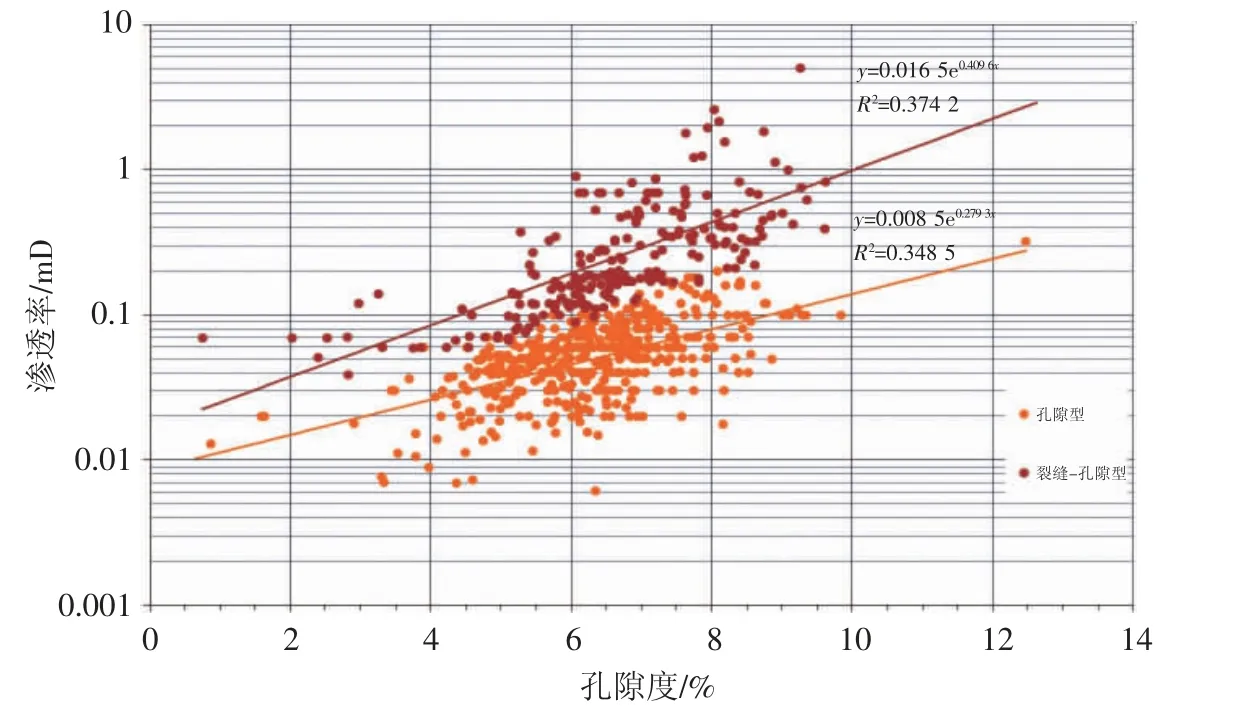
图1 蓬莱107 井区须二段不同储集类型砂岩孔渗关系图

根据上述孔渗分级下限，结合研究区须二段已有钻井的含气性、测试、试采等与孔渗分布区间的相关性，将渗透率大于0.500 mD，且孔隙度大于14.5%的孔隙型储层和孔隙度大于9.0%的裂缝-孔隙型储层评价为好储层，渗透率在0.300～0.500 mD，孔隙度大于12.5%的孔隙型储层与孔隙度大于7.5%的裂缝-孔隙型储层评价为较好储层，渗透率在0.085～0.300 mD，孔隙度大于8.0%的孔隙型储层和孔隙度大于4.0%的裂缝-孔隙型储层评价为中等储层，渗透率小于0.085 mD，孔隙度小于8.0%的孔隙型储层和孔隙度小于4.0%的裂缝-孔隙型储层评价为差储层。

本次研究将中等储层、较好储层和好储层较为发育的层段和区域定义为储渗体，也就是说储渗体下限为渗透率大于0.085 mD，孔隙度大于8.0%的孔隙型储层和孔隙度大于4.0%的裂缝-孔隙型储层，它们是储渗体内的主要储层，研究区须二段储渗体发育层段在圈闭有效时具有产出工业气流的能力。

2 储渗体预测模型分析

2.1 须二段砂岩测井响应特征

蓬莱107 井区须二段储集岩岩石类型为中粒岩屑长石砂岩及长石岩屑砂岩；物性表现为低孔、低渗、高束缚水饱和度特征；电性特征表现为低自然伽马、低电阻、高声波时差特征，从声波时差、自然伽马、电阻关系图可知，储渗体电性特征表现为：GR 集中在60～90 API，声波时差在64～72 μs/ft，电阻率在15 Ω·m 以上，集中在15～35 Ω·m。虽然通过曲线可大致总结出储渗体的电性特征，但此特征被包含在了砂岩的电性特征区间值之内，依然无法与砂岩电性特征所区分开来。

根据研究区须二段取心井岩心发育裂缝与砂岩渗透性关系可知，岩心裂缝发育程度与渗透性关系密切，裂缝发育时，渗透性好，易于形成储渗体，同时成像测井上裂缝发育层段也表现出较好的渗透性，如蓬莱107 井在成像测井资料2 405、2 414 m 见多条明显构造缝，渗透性好，加砂压裂后测试获高产油气流，获气51.99×104m3/d，油9.6 t/d（图2）。但裂缝发育特征在常规测井信息上的表现并不明显。

图2 蓬莱107 井须二段裂缝电性响应特征

由此可知蓬莱地区须二段储渗体和一般砂岩在常规测井上的特征较为相似，因此，无法直接根据常规测井信息区分储渗体与其他的一般砂岩。本次研究中也曾尝试过直接预测渗透率来识别储渗体，但渗透率与单一的常规测井信息关系也不明显，无论是线性预测模型还是非线性预测模型，预测准确率均达不到要求。这可能是须二段复杂的储层类型造成的结果。

2.2 储层类型非线性预测模型

针对蓬莱地区测井曲线与储层类型非线性的特点，本次研究选择了适用于此情况的随机森林分类算法来对须二段储层类型进行预测，以达到在砂岩中区分不同类型储层的目的。随机森林分类算法具有参数少，建模快的特点，可运用随机森林算法中的分类算法来建立分类模型。

随机森林分类算法，即是运用随机森林算法对样本进行分类预测。随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支-集成学习方法。从直观角度来解释，每个决策树都是一个分类器，那么对于一个输入样本，N 个树会有N 个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出。

随机森林通过构造不同的训练集增加分类模型间的差异，从而提高组合分类模型的外推预测能力。通过k 轮训练，得到一个分类模型序列{h1（X），h2（X），…，hk（X）}，再用它们构成一个多分类模型系统，该系统的最终分类结果采用简单多数投票法。最终的分类决策：

式中：H（x）-组合分类模型；hi-单个决策树分类模型；Y-输出变量；I（·）-示性函数。式（1）说明了使用多少投票决策的方式来确定最终的分类。

将原始数据中的输出参数（本文参与计算数据为AC、DEN、GR、RT 等测井曲线）向下传递给每一个决策树，每一个决策树单独做出分类决策，最后以投票的形式，看哪种类别最多就判断为输出值（图3）。

图3 随机森林原理示意图

3 储渗体预测应用

本文模型的建立，使用了Python 语言，所用程序为Python3.6。选用取心数据较多的蓬莱107 井和蓬莱6 井进行建模。将未参与建模的蓬莱11 井取心数据作为检验数据。通过对比模型预测储层类型与实际取心储层类型可知，模型对于储层类型的预测较为准确。同时，与作为检验数据的蓬莱11 井实测数据相比，储层预测正确率为96%，达到了预测要求精度。将预测模型应用于蓬莱002-X7 井可得到其储渗体预测结果（图4），该井部分井段电成像图见图5。

图4 蓬莱002-X7 井储渗体预测图

图5 蓬莱002-X7 井2 391～2 395 m、2 401～2 405 m 电成像图

将预测模型应用于蓬莱002-1-X1、蓬莱002-2-X1 等多口井，对其须二段进行储层类型预测，获得了重点井须二段砂岩中的储层类型分布。

对典型井须二段中裂缝-孔隙型储层的厚度以及射孔段中裂缝-孔隙型储层所占比例进行了统计，见表2，同时获得了典型井须二段砂岩裂缝-孔隙型储层厚度分布。从表2 可以看出，蓬莱002-1-X1、蓬莱002-3-X1 等中高产井的裂缝-孔隙型储层厚度较厚，干井和蓬莱002-2-X1 井的裂缝-孔隙型储层厚度较薄，与实际相符。

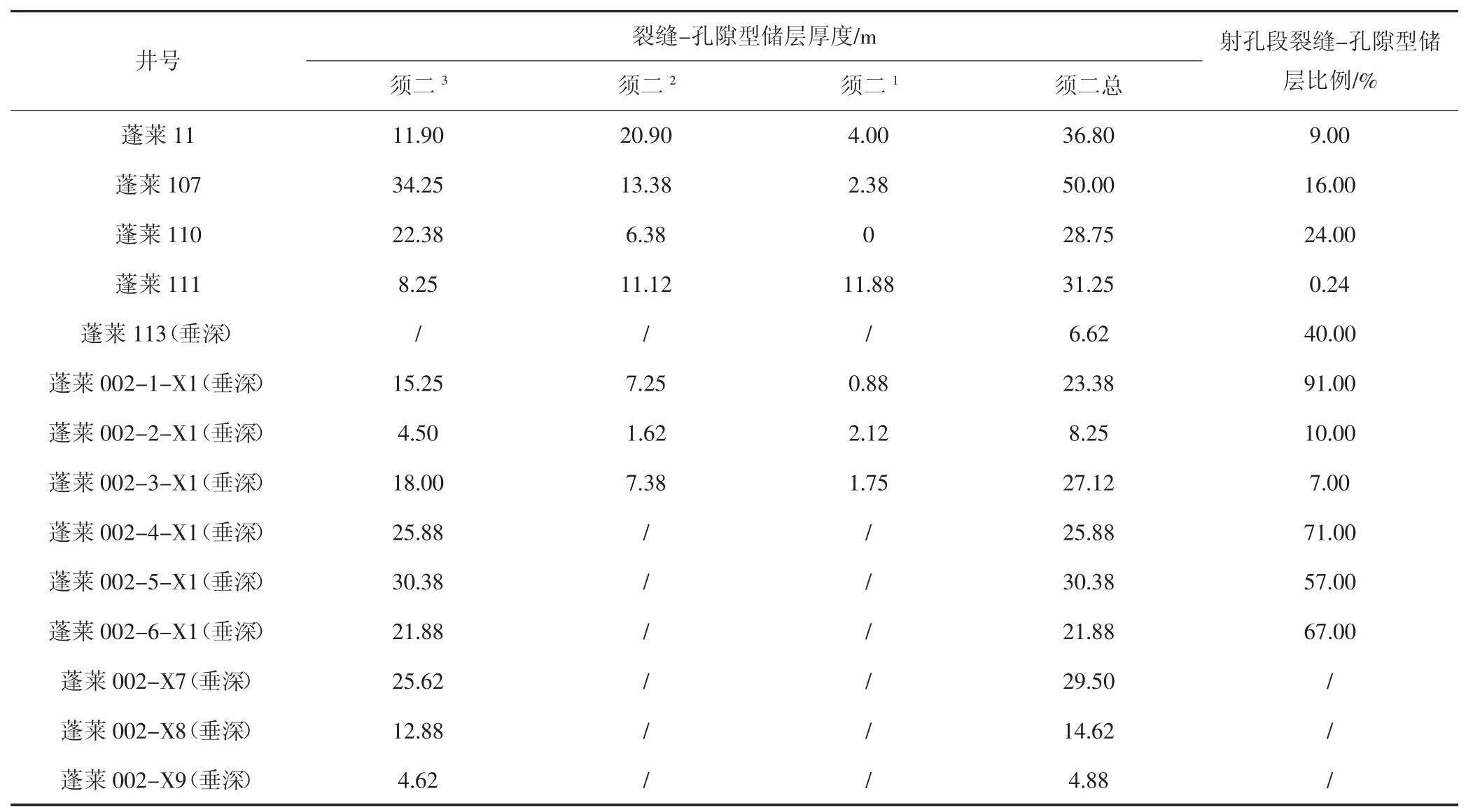
表2 须二段裂缝-孔隙型储层厚度及在射孔段砂岩中的比例分布表

4 结论

（1）综合运用研究区现有钻井的含气性、测试、试采等资料以及孔渗分布区间的相关性分析，重新确定了本文的储渗体定义。针对蓬莱地区须二段砂岩取心少且不系统、孔隙结构复杂导致孔渗相关关系差的特点，利用随机森林分类算法实现了单井储层类型纵向分布预测。

（2）研究区须二段储渗体裂缝发育程度与渗透性关系密切。但裂缝发育特征在常规测井信息上的表现并不明显，识别有一定的难度。

（3）运用随机森林分类算法建立的储层类型分类模型，储层预测正确率为96%，达到了预测要求精度。由此进行的储渗体测井解释，蓬莱002-1-X1、蓬莱002-3-X1 等中高产井的裂缝-孔隙型储层厚度较厚，与实际相符。