提升小学生数学符号意识的教学策略

■刘萍

符号意识是指能够理解并且运用符号表示数、数量关系和变化规律；知道使用符号可以进行运算和推理，得到结论。 建立符号意识有助于学生理解符号的使用，是数学表达和进行数学思考的重要形式。 《义务教育数学课程标准（2022 年版）》（以下简称《课标》）指出，“在数学课堂中，应当重视发展学生的数感、量感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识”[1]，并在课程内容中将“符号意识”作为十一个核心概念之一提出，由此可见，符号意识是小学生必备的一种数学素养。

一、小学生数学符号意识发展的特点

（一）小学生对数学符号的理解易混淆

小学生对数学符号的感知侧重于符号在情境中表达出来的含义，如果脱离具体的情境，其对符号的含义与分辨能力会明显下降。 例如，学生对x与x+2 能够比较容易分辨出大小，但是对2x 与x+2 的比较，就产生出了感知困难。 还有学生将长度单位符号化6m(6 米)中的m 与6+m 中的未知数m混淆在一起。

因为小学生的思维还存在比较明显的具象性特点，喜欢利用具体事物来进行描述，而利用符号意识来逐步建立学生的抽象意识，提升学生符号感知灵活性就非常必要。

（二）小学生数学符号的应用意识明显不足

通常1-3 年级在情境化的具象教学模式中学习，致使学生容易产生惯性思维，偏爱用具体化的解题方法，而不喜欢运用符号来代替数量关系解决问题。

归根结底还是学生缺乏自主运用符号的意识，在日常学习中，学生运用数学符号练习机械化，只会套用教师课堂上的内容，缺乏自己对知识的思考，教什么用什么，用完就丢掉。

（三）小学生的数学符号运算水平需要提高

通过调研我们发现，学生对符号的运算能力还不够熟练，所以在运用符号计算过程中错误率居高不下。对运算法则及运算技巧的掌握不强是导致学生符号运算能力水平无法提升的原因，而反复的错误导致了学习自信心下降，产生自我怀疑，导致对符号运算出现畏惧心理。 那么，循序渐进地加强学生符号运算能力就非常有必要。

（四）小学生对数学符号的推理能力需要加强

利用数学符号来解决问题需要学生有较强的推理能力，在能运用数学符号表示数以及数量关系的基础上，学生还需要利用自身思维去发现其中变化的规律，并对这种规律加以利用，迁移到对问题的思考中，提出猜想，再借助数学符号来进行推理过程的表达，验证猜想。 通过一系列思维对数学符号的动态推理，达到解决问题的目的，但这种综合性运用非常考验学生数学符号推理能力，需要有针对性的在日常训练中运用提升。

二、提升小学生符号意识的教学策略

（一）指导学生掌握符号工具，提高学生符号感知与理解能力

《课标》提出，培养学生符号意识要使学生学会利用数学符号进行运算。 为此，教师在教学中要让学生理解符号的含义，并在符合运算规律的基础上进行正确运算，从而掌握符号工具。

如图1，在进行以下练习时，学生在理解了符号“h”表示“小时”，符号“5h”表示“5 个小时”，符号“10h”表示“10 小个时”，并且知道5h 和10h 中间省略了乘号的基础上，正确计算出了5 个小时、10个小时滴水多少桶的问题，进而在运算的时候掌握了一天可以用符号“24h”简洁地表示。

图1

在培养学生符号意识的时候，教师要引导学生多使用符号进行一些概念的表示，这集中体现在方程的运算方面。

如图2，今年妈妈的年龄是淘气的3.7 倍，淘气比妈妈小27 岁，问：今年妈妈和淘气各多少岁？

图2

淘气1 岁，妈妈3.7 岁

淘气2 岁，妈妈7.4 岁

淘气3 岁，妈妈11.1 岁

……

学生感知，当淘气x 岁时，妈妈就是3.7x 岁，通过两人年龄差不变的这一规律，学生可以得出“今年妈妈的年龄-淘气今年的年龄=27 岁”，学生在教师的引导下列出方程“3.7x-x=27”。 教师利用问题引导，展现数字抽象化为字母符号的过程，增强了学生的符号使用思维体验，锻炼了学生的运算能力。

（二）指导学生学会转换思维，提高学生的符号表征与运算能力

《课标》要求学生能利用数学符号表示数、数量关系以及变化规律，要求学生不仅理解数学符号，而且会进行数学符号的表达以及相互转换。

如图3，在学习三角形的面积一课时，学生将两个完全相同的三角形拼合成平行四边形推导出三角形的面积公式时，就经历了从文字语言到数学语言“三角形的面积是底乘高除以2”，最后到符号语言“S=ah÷2”的过程，在不断转换的过程中加深了对三角形面积公式S=ah÷2 的符号表示的理解。

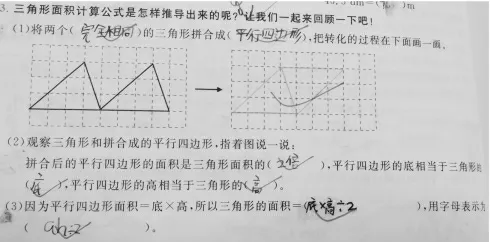
图3

如图4，在学习梯形的面积一课时，学生推导出梯形的面积公式，也经历了从文字语言到数学语言“梯形的面积是上底与下底的和乘高除以2”，最后到符号语言“S=（a+b）h÷2”的过程，在不断转换的过程中加深了对梯形面积公式S=（a+b）h÷2 的符号表示的理解。

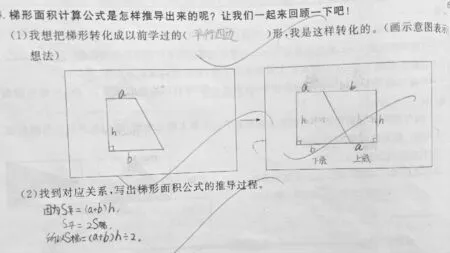
图4

（三）指导学生学习符号思维，提高学生的符号抽象与推理能力

《课标》提出，培养学生符号意识要使学生学会利用数学符号进行推理， 即培养学生符号思维能力。 为此，教师可以在教学中引导学生用数学符号进行推理与思考。

如图5，学生利用题目找到长宽高之间的数量关系，并用符号表示，找到等量关系式，列出方程才将这个复杂问题解决。 学生把宽设为符号x，通过推理可知长是符号1.5x，高为符号x÷2。 最后教师引导学生总结如何将如此复杂的问题解决，学生会发现在推理与思考中运用符号思维将复杂问题变得简单，进而积累了在推理中运用符号的思考经验。

图5

如图6，看着复杂的问题，学生画了几条线分一分，马上理清了一张桌子、两张桌子、三张桌子的桌子数量与可坐人数的关系，由具体到抽象，进行合情推理，进而理清桌子的数量与可坐人数之间的数量关系是“桌子的数量×4+2=可以坐的人数”，最后写出字母表达式，4n+2 就是学生在推理中运用符号思维分析问题的具体表现。

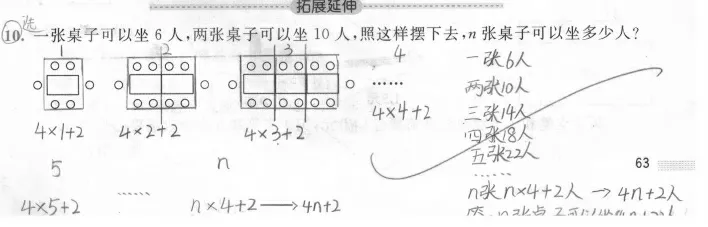
图6

（四）指导学生习得模型思想，提高学生的符号应用与推理能力

学生在不断的学习中正确理解了每个符号的含义，会进行符号运算，如果能够在此基础上习得模型思想，那么学生在解决复杂的变形问题时就会有质的飞跃。所谓的模型思想就是学生掌握一些基本的模型符号公式，例如长方体的表面积公式、圆柱的体积公式等都是基本模型公式。那么在解决有关的变形问题时，学生会以基本公式为基础，进行公式的变形与应用，在这个过程中学生的符号应用与推理能力得到了提高。

如图7，学生在解决如图所示钢管的体积时，首先想到了之前学习过的圆柱的体积公式，推断出给出的钢管相当于是两个大小不同的同心圆柱，那么用大圆柱的体积减小圆柱的体积就是钢管的体积，两个圆柱的高是相等的，半径大小不同，学生根据观察出的以上信息推理得出钢管的体积公式并用符号表示。 学生为了区分半径r 的大小不相等，在符号的下面加了简单的汉字“大与小”进行区分，可见学生对符号的感知与理解很到位，并且习得了之前学过的圆柱的体积公式这个模型思想，进而解决复杂问题时，可以准确应用符号并进行推理。

图7