基于sigmoid-sinh分段函数的变步长FxLMS算法

李 飞，黄 双，郭 辉，徐 洋，傅 伟

(1.上海工程技术大学 机械与汽车工程学院, 上海;2.东华大学 机械工程学院, 上海;3.淄博市技师学院,山东 淄博)

噪声主动控制采用声波的相消干涉原理,被广泛应用于各个领域,如航空航天、电梯、汽车等[1-2]。在噪声主动控制系统中,FxLMS(filter-x least mean square)算法结构简单,吸引了较多学者对其进行研究[3-7]。采用固定步长的传统FxLMS算法无法同时保证收敛速度快和稳态误差小。为解决这一问题,许多学者对变步长FxLMS算法进行研究。刘宁宁等[8]提出一种基于反正切函数的迭代变步长FxLMS(iterative variable step-size FxLMS, IVS-FxLMS)算法,利用该算法对汽车驾驶员耳侧不同阶次的发动机噪声进行主动控制效果仿真,结果表明,车内发动机阶次噪声得到有效抑制。李涛等[9]在sigmoid函数的基础上,提出一种快速、平滑的变长FxLMS(fast and smooth FxLMS, FSFxLMS)算法,并通过列车低频噪声仿真对算法性能进行验证,结果表明,FSFxLMS算法能够提高收敛速度和稳态误差之间的均衡性。张帅等[10]结合归一化方法与反正切函数,提出一种变步长改进的FxLMS(variable step-size modified FxLMS, VS-MFxLMS)算法,该算法的收敛速度和稳态误差都有大幅度的提升。上述这些算法在一定程度上解决了传统FxLMS算法无法同时保证收敛速度快和稳态误差小的问题。但是,目前提出的变步长算法大多选取一种函数为基础进行变形,由于单一函数性能的限制,改进算法无法使收敛速度以及稳态误差同时达到最优。

基于sigmoid函数的FxLMS(SFxLMS)算法收敛速度快和sinh函数的FxLMS(ShFxLMS)算法稳态误差小的优点,提出一种基于sigmoid-sinh分段函数的FxLMS(SSFxLMS)算法,并分别使用FxLMS、SFxLMS、ShFxLMS和SSFxLMS算法对高斯白噪声以及实测簇绒地毯织机噪声进行主动控制,验证SSFxLMS算法的有效性。

1 FxLMS算法

FxLMS算法根据误差信号不断调整滤波器权值,直到滤波器输出一个理想的抵消信号对噪声进行抵消,达到降噪目的。FxLMS算法框图如图1所示。

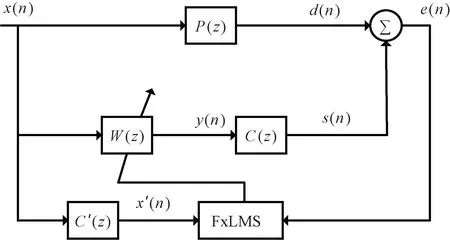
图1 FxLMS算法框图Fig.1 Block diagram of FxLMS algorithm

FxLMS算法的计算过程如下：

1)生成一个期望信号d(n)。该信号由原始噪声信号x(n)经过初级通道得到,即

d(n)=P(n)*x(n)

(1)

式中：n为当前时刻点;*为线性卷积运算;P(n)为初级通道传递函数P(z)的脉冲响应。

2)生成抵消信号s(n)。该信号由噪声信号经过滤波器滤波,再经过次级通道得到,即

y(n)=wT(n)x(n)

(2)

s(n)=C(n)*y(n)

(3)

式中：y(n)为滤波器输出;w(n)为滤波器权值;C(n)为次级通道传递函数C(z)的脉冲响应。

3)生成误差信号e(n)。该信号由期望信号与抵消信号叠加得到,即

e(n)=d(n)-s(n)

(4)

4)更新FxLMS控制器。根据LMS(least mean square)算法对滤波器的权值进行更新,其计算式为

w(n+1)=w(n)-2μe(n)x′(n)

(5)

式中：μ为迭代步长,主要影响算法的收敛速度与稳态误差;x′(n)为滤波后信号,是噪声信号经过次级通道传递函数C′(z)得到的响应,C′(z)通过对次级通道传递函数C(z)的幅值和相位特性辨识得到。滤波器的输出信号到达误差传感器处需要经过次级通道,会产生一定的延时,引入C′(z)能够解决这一问题。理论上,C(z)和C′(z)是完全相等的。x′(n)的计算式为

x′(n)=C′(n)*x(n)

(6)

在上述过程中,滤波器权值被不断调整,最终滤波器能够生成与噪声信号完全抵消的信号,从而实现降噪。

2 SSFxLMS算法

2.1 SSFxLMS算法的提出

变步长FxLMS算法的原理是通过正弦函数、反正切函数等建立算法步长μ与误差信号e(n)之间的关系。在算法开始迭代即误差信号较大时,取较大步长,从而提高算法收敛速度;在算法将要结束迭代即误差信号较小时,取较小步长,从而减小算法稳态误差。变步长算法的权值更新计算式为

w(n+1)=w(n)-2μ(n)e(n)x′(n)

(7)

SFxLMS算法采用sigmoid函数进行步长调整,其步长更新计算式为

(8)

式中：α1为曲线形状调控参数,控制曲线形状;β1为控制曲线最大值。当β1固定,α1取不同值时,步长随误差信号变化的曲线如图2所示。

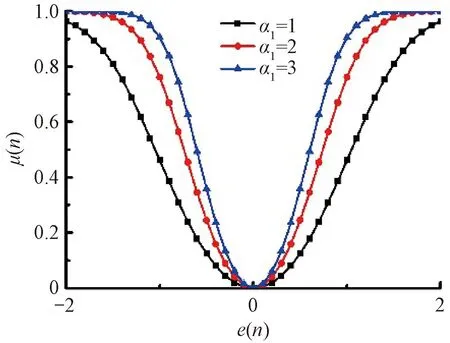
图2 SFxLMS算法的步长随误差信号变化的曲线Fig.2 Curve of step size of SFxLMS algorithm changing with error signal

由图2可知：当α1值越大,曲线底部越尖锐,这导致在误差信号很小时步长为一较大值,从而使稳态误差较大;当α1值越小,曲线底部虽然会变得平坦,但在误差信号较大时,其步长较小,从而导致收敛速度变慢。因此,SFxLMS算法的特点为收敛速度快但稳态误差较大。

ShFxLMS算法采用sinh函数进行步长调整,其步长更新计算式为

(9)

式中：α2、β2为曲线形状调控参数。

当固定β2值,α2取不同值时,ShFxLMS算法的步长随误差信号变化的曲线如图3所示。由图3可知,不论α2值是大还是小,曲线的底部都比较平坦,在误差信号很大时采用小步长,这可以保证较低的稳态误差,但会使得收敛速度变慢,因为曲线过于平坦会导致μ过早地降低到一个较小值。因此,ShFxLMS算法的特点为稳态误差小但收敛速度相对较慢。

图3 ShFxLMS算法的步长随误差信号变化的曲线Fig.3 Curve of step size of ShFxLMS algorithm changing with error signal

综合考虑SFxLMS算法和ShFxLMS算法的优缺点,本文提出一种分段函数变步长SSFxLMS算法,其步长更新计算式为

(10)

式中：α3、α4、β3、β4为曲线形状调控参数,控制两段曲线的形状;b为函数选择阈值,其值大小决定算法在何种条件下对步长更新函数进行转换。算法迭代前期时,考虑到SFxLMS算法收敛速度快的特点,选取SFxLMS算法对步长进行更新,加快收敛速度;当算法将要收敛时,考虑到ShFxLMS算法稳态误差小的特点,选取ShFxLMS算法对步长进行更新,降低稳态误差。

2.2 计算量分析

计算量是评估算法性能的重要指标。取算法每更新一次所需的乘法、加法以及指数运算的次数对FxLMS、SFxLMS、ShFxLMS、SSFxLMS算法的计算量进行比较。算法每次迭代时,产生计算量的部分主要有参考信号滤波(式(6))、滤波器输出(式(2))、滤波器权值更新(式(5))。因此,本文主要针对这3个过程进行计算量分析,假设信号的长度为L,得到4种算法每次迭代需要的计算量如表1所示。从表1可知,SSFxLMS算法每次更新前需要对e(n)与b值进行一次比较,确定更新所用函数,相较于SFxLMS、ShFxLMS算法,只多了一次比较运算,增加的计算量可以忽略。

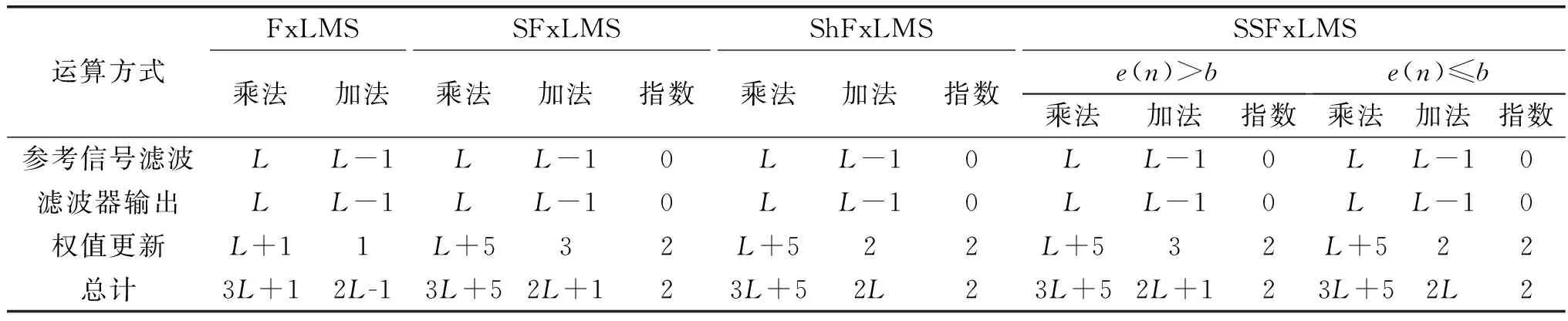
表1 4种算法计算量Table 1 Calculation amount of four algorithms

3 算法参数的选取

算法参数对算法的性能产生重大影响。在进行仿真之前,必须不断调整算法的参数,使得算法的性能达到最优,通过试凑法调整参数很难保证算法性能达到最优。因此,考虑到蚁狮算法在进行参数优化时具有全局寻优性强、收敛精度高等优点,本文使用蚁狮算法对SFxLMS、ShFxLMS以及SSFxLMS算法的参数进行优化。

3.1 蚁狮算法简介

蚁狮算法[11]借鉴了蚁狮捕食蚂蚁的机制,将待优化参数转变为蚂蚁和蚁狮的位置,每次迭代时,蚂蚁和蚁狮位置随机更新,根据其位置计算出各自适应度值,将蚂蚁和蚁狮中适应度最优个体保存为精英,精英即为每一次迭代中适应度值最优的个体。迭代完成后,精英的位置就是参数最优值。图4为蚁狮算法的工作流程图。

图4 蚁狮算法流程图Fig.4 Flow chart of ant-lion algorithm

蚁狮算法的具体优化步骤：首先,对蚂蚁、蚁狮的位置进行随机初始化,得出各自的适应度值,将适应度值最优的个体作为精英保存起来。其次,让蚂蚁在限定的范围内随机游走,得到新一代蚂蚁的适应度值,并将蚂蚁与蚁狮中适应度值最优的设为蚁狮,将蚁狮和精英中适应度值最优的设为精英。最后,判断是否满足算法终止迭代的条件。如果满足终止迭代条件,输出精英的位置,即参数最优解;如果不满足终止迭代条件,继续让蚂蚁游走,不断循环,直到满足终止迭代条件。

3.2 设定优化目标

使用蚁狮算法前,需要选取优化的目标函数。为得到使算法降噪效果最优的参数值,选取误差绝对值的平方值最小为优化目标,对SFxLMS、ShFxLMS以及SSFxLMS算法的步长更新公式进行分析,得出优化目标函数。

对式(8)进行变换,得到SFxLMS算法参数优化的目标函数如式(11)所示。

(11)

对式(9)进行变换,得到ShFxLMS算法参数优化的目标函数如式(12)所示。

(12)

对式(10)进行变换,得到SSFxLMS算法参数优化的目标函数如式(13)所示。

(13)

4 仿真验证

为验证SSFxLMS算法的性能,分别用FxLMS、SFxLMS、ShFxLMS、SSFxLMS算法对高斯白噪声和采集的簇绒地毯织机噪声进行控制,然后对比分析噪声控制效果。

4.1 高斯白噪声仿真

设置高斯白噪声为输入信号,其均值为0、方差为0.5,仿真时间为2 s。用蚁狮算法对SFxLMS、ShFxLMS、SSFxLMS算法进行参数优化。

4.1.1 高斯白噪声仿真参数优化

为确定各个参数的取值范围,在Simulink软件中搭建3种算法模型,以高斯白噪声为输入。考虑收敛性和噪声控制后误差信号变化情况,各算法的参数取值范围如表2所示。

表2 高斯白噪声控制时算法参数取值范围Table 2 Value range of algorithm parameters for Gaussian white noise control

设定优化目标为误差绝对值的平方值最小,SFxLMS、ShFxLMS、SSFxLMS算法的目标函数分别如式(11)～(13)所示。每次优化时,蚁狮算法的迭代次数为50、蚂蚁个数为20。在程序运行后,得到3种算法的最优参数值如表3所示。

表3 高斯白噪声控制时参数最优值Table 3 Optimal values of parameters for Gaussian white noise control

4.1.2 高斯白噪声控制

FxLMS算法的步长取μ=0.1,另外3种算法的参数取表3中经蚁狮算法优化得到的值。在Simulink软件中进行高斯白噪声主动控制仿真,得到FxLMS、SFxLMS、ShFxLMS、SSFxLMS算法控制后误差曲线如图5所示。

图5 4种算法对高斯白噪声主动控制时的误差信号曲线Fig.5 Error signal curves of four algorithms for active control of Gaussian white noise

由图5可知,3种变步长算法的高斯白噪声控制效果都优于FxLMS算法,其中本文提出的SSFxLMS算法的控制效果最优,SFxLMS、ShFxLMS算法的控制效果相似。为更好区分FxLMS、SFxLMS、ShFxLMS和SSFxLMS算法在时域的控制效果,计算4种算法的平均绝对误差(mean absolute error,MAE)值,即每个采样点的噪声信号误差值的绝对值取平均值,其计算式为

(14)

式中：M为噪声信号平均绝对误差;N为采样点数量。

4种算法的M值计算结果如表4所示。由表4可知,SSFxLMS算法的M值相对于FxLMS、SFxLMS、ShFxLMS算法分别降低了95.2%、93.8%、93.9%。由此说明SSFxLMS算法在用于高斯白噪声的控制时具有更小的稳态误差。

表4 4种算法对高斯白噪声主动控制时的M值

为对比4种算法的收敛速度,引入平均降噪量[12](average noise reduction,ANR)作为评价指标,其计算式为

(15)

Ae(n)=ξAe(n-1)+(1-ξ)|e(n)|

(16)

Ad(n)=ξAd(n-1)+(1-ξ)|d(n)|

(17)

式中：R为平均降噪量;Ae(n)为误差信号e(n)的递推估计;Ad(n)为期望信号d(n)的递推估计;ξ为遗忘因子。

初始条件为Ae(n)=0,Ad(n)=0,ξ=0.999 9。迭代前期,曲线斜率越大,则收敛速度越快;迭代后期,曲线位置越低,稳态误差越小。4种算法的R值曲线如图6。

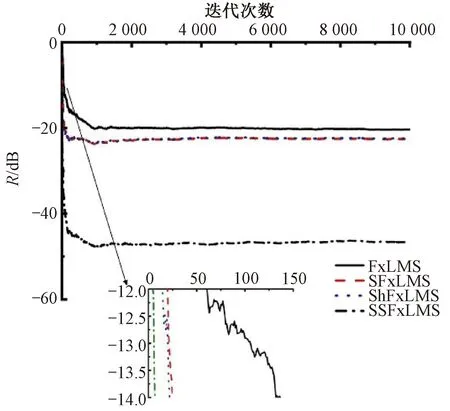
图6 4种算法对高斯白噪声主动控制时的R曲线Fig.6 R curves of four algorithms for active control of Gaussian white noise

由图6可知,FxLMS算法收敛速度最慢,SFxLMS和ShFxLMS算法的收敛速度相似,SSFxLMS算法的收敛速度远超另外3种算法,并且其在迭代后期的稳态误差最小。

4种算法在频域上的高斯白噪声控制效果如图7所示。由图7可知,SSFxLMS算法的控制效果整体优于另外3种算法。为精确比较4种算法的频域控制效果,对频域为0～500 Hz的平均降噪量进行计算,得到FxLMS、SFxLMS、ShFxLMS、SSFxLMS算法的平均降噪量分别为8.3、11.3、11.3、34.2 dB,其中SSFxLMS算法的平均降噪量相对于另外3种算法都有不同程度的提升。

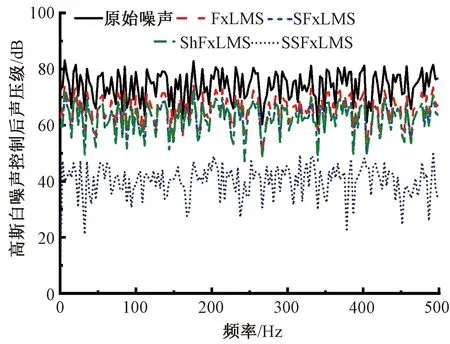
图7 4种算法对高斯白噪声主动控制的频域效果图Fig.7 Frequency domain effect diagram of four algorithms for active control of Gaussian white

综上所述,在对高斯白噪声进行控制仿真时,SSFxLMS算法的收敛速度以及稳态误差都优于另外3种算法。

4.2 簇绒地毯织机噪声仿真

纺织车间内有许多大型纺织机械,工作时会产生高强度噪声,长时间的高强度噪声会对纺织工人的身体健康造成不可修复的损害[13]。徐洋等[14]对簇绒地毯织机噪声在频带上的分布进行了分析,结果表明,簇绒地毯织机噪声信号在0～500 Hz的低频段占有很大一部分。因此,本文以簇绒地毯织机为例,对其低频噪声进行主动控制。

4.2.1 织机噪声信号采集

依照GB/T 7111.6—2002《纺织机械噪声测试规范 第6部分：织造机械》的要求对簇绒地毯织机噪声进行采集。簇绒地毯织机以350 r/min的转速空载运行,麦克风监测点布置在操作人员工作区域,距机器外表面0.5 m,距地面高1.6 m,采样频率为51 200 Hz,时间为10 s,从中选取5～7 s的噪声进行控制,其噪声信号波形如图8所示。

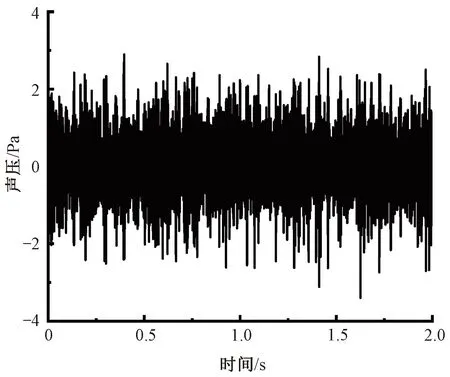
图8 簇绒地毯织机噪声信号波形图Fig.8 Waveform of tufted carpet loom noise

4.2.2 织机噪声控制参数优化

为确定织机噪声控制时不同算法参数的取值范围,在Simulink软件中搭建SFxLMS、ShFxLMS、SSFxLMS算法模型,以织机噪声为输入。考虑收敛性和噪声控制后误差信号变化情况,各算法的参数取值范围如表5所示。

表5 织机噪声控制时算法参数取值范围Table 5 Value range of algorithm parameters for loom noise control

每次优化时,蚁狮算法的迭代次数为50、蚂蚁的个数为20,运行程序后,得到各种算法最优参数值如表6所示。

表6 织机噪声控制时算法参数最优值Table 6 Optimal values of algorithm parameters for loom noise control

4.2.3 织机噪声控制

FxLMS算法的步长取μ=0.1,SFxLMS、ShFxLMS、SSFxLMS算法的参数取表6中经蚁狮算法优化后的值,分别用4种算法对簇绒地毯织机噪声进行控制,得到控制后误差信号对比图、R曲线以及频域控制效果图如图9～11所示,M值如表7所示。

表7 4种算法对织机噪声主动控制时的M值

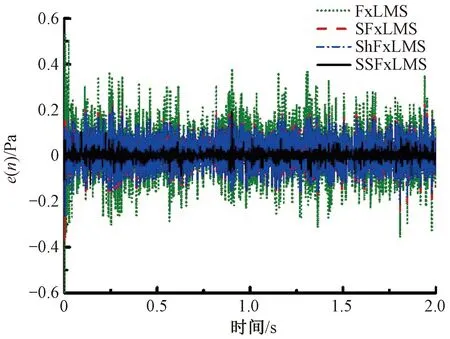
图9 4种算法对织机噪声主动控制时的误差信号曲线Fig.9 Error signal curves of four algorithms for active control of loom noise

由图9可知,传统的FxLMS算法的噪声控制效果最差,采用SSFxLMS算法的噪声控制效果最好。由图10可知,SSFxLMS算法的收敛速度、稳态误差都优于另外3种算法。由图11可知,FxLMS、SFxLMS、ShFxLMS、SSFxLMS算法在频域为0～500 Hz的平均降噪量分别为6.9、8.8、8.9、24.2 dB,SSFxLMS算法的平均降噪量相较于另外3种算法至少提高15 dB。由表7可知,SSFxLMS算法的M值最小,相较于FxLMS、SFxLMS和ShFxLMS分别降低了90.6%、87.9%、88.0%。

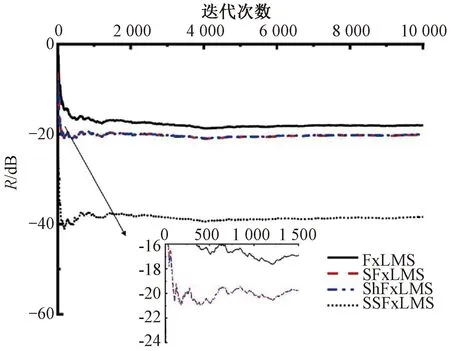
图10 4种算法对织机噪声主动控制时的R曲线Fig.10 R curves of four algorithms for active control of loom noise

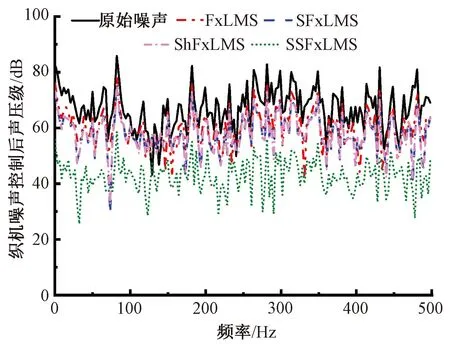
图11 4种算法对织机噪声主动控制的频域效果图Fig.11 Frequency domain effect diagram of four algorithms for active control of loom noise

通过对比发现,对簇绒地毯织机噪声控制时,相较于另外3种算法,SSFxLMS算法在时域上稳态误差最小,在频域上平均降噪量最高,且收敛速度最快。因此,SSFxLMS算法不仅解决了FxLMS算法无法同时确保收敛速度快与稳态误差小的问题,而且其性能也优于SFxLMS、ShFxLMS算法。

5 结 论

本文结合sigmoid函数与sinh函数的特点,提出一种基于sigmoid-sinh分段函数的变步长SSFxLMS算法。通过建模仿真发现：SSFxLMS算法在对高斯白噪声进行控制时,其平均绝对误差降低了93.8%以上,频域为0～500 Hz的平均降噪量提高22.9 dB以上,且收敛速度更快;对簇绒地毯织机噪声进行控制时,其平均绝对误差降低了87.9%以上,平均降噪量提高15 dB以上,收敛速度也最快。结果表明,所提出的SSFxLMS具有较好的噪声控制效果。