高频聚焦超声声场和温度场的仿真研究∗
徐 慧 陈 思 幸柏成 单天琪,2 赵 渊,2
(1 超声医学工程国家重点实验室 重庆医科大学生物医学工程学院 重庆 400016)
(2 超声医疗国家工程研究中心 重庆 401121)
0 引言
聚焦超声(Focused ultrasound,FU)作为一种极具潜力的非侵入式肿瘤治疗技术,在临床治疗和科学研究中得到了广泛的关注[1-2]。其原理是利用聚焦于组织内部的高强度超声产生的热效应使焦域组织温度短时间升至60◦C 以上,使组织发生热凝固坏死,而焦域以外组织无明显损伤[3]。由于超声具有很好的组织穿透性和热沉积性,FU 已被证实对骨肿瘤[4]、子宫肌瘤[5]、肝癌[6]、胰腺癌[7]、乳腺癌[8]等实体肿瘤疾病有较好的治疗效果。近年来,随着超声和换能器技术的发展,FU 的频率已经向7 MHz 甚至更高频率拓展,高频FU 在妇科和皮肤科等领域展示出巨大的应用潜力。一项2015 年的临床实验结果表明,高频FU 是一种安全、有效、复发率低的治疗外阴非肿瘤性上皮病变的方法[9]。2009 年,高频FU 设备被FDA 批准用于皮肤美容受到了广泛关注。高频FU 通过利用各种换能器在所需深度形成微损伤,破坏胶原蛋白,使新的组织形成和胶原蛋白再生,从而达到皮肤紧致和提升的目的[10]。2016年,Werschler等[10]为评估定制的可视化微FU 治疗对于紧致人体面部和颈部组织的有效性和安全性,使用中心频率7 MHz、焦深分别为3 mm 和4.5 mm 的换能器对实验者进行治疗。实验结果表明,90%∼100%的患者均有明显改善,其中79%患者面部松弛得到了改善,58%的患者皱纹减少以及47%的患者皮肤变光滑。
Alam等[11]为评估FU紧致面部皮肤治疗方法的安全性和有效性,使用中心频率为7 MHz、焦深为4.5 mm 和3 mm 的聚焦换能器对受试者的前额、太阳穴、脸颊进行治疗(工作参数为能量:0.75∼1.05 J;工作时间:25∼40 ms),临床实验结果表明,FU 是一种安全有效的面部皮肤紧致方法。但是该研究缺乏理论仿真指导,无法优化换能器以及治疗参数,治疗效果和治疗的安全性有待进一步提高。宿慧丹等[12]通过有限元仿真方法模拟了高强度聚焦超声(High intensity focused ultrasound,HIFU)焦域的声场和温度场分布,并讨论了换能器参数对焦域温度分布的影响。但是未考虑声波非线性传播和组织热黏性对温度场的影响,温度估计不够精确。Haddadi等[13]以中心频率为1.1 MHz的聚焦换能器、输入功率为8.3∼134 W 为研究范围,建立了FU 作用于肝组织的非线性热黏性仿真模型。但是该模型只考虑了肝脏和水两种介质,未考虑皮肤对声场传播的影响。Mortazavi等[14]建立了中心频率为4 MHz、曲率半径为8.6 mm 的聚焦换能器作用于多层组织的非线性声传播模型。到目前为止,还没有临床常用的7 MHz 高频FU 辐照多层组织的非线性热黏性声传播及传热模型的相关报道。
前人的数值仿真研究中[13,15]大多以肝脏作为目标组织,并只考虑了水和软组织两层结构,使用的换能器频率为1 MHz,聚焦深度较深。高频FU的不同之处在于:(1) 换能器中心频率高、曲率半径短、超声在多层复杂组织中传播受到的影响较大,声传播方式较为复杂;(2) 消融所需时间短,焦域在毫秒级的时间内即可达到凝固性坏死所需温度,达到消融的目的。这使得常规FU 消融研究中建立的线性声传播及生物传热理论无法真实反映高频FU在多层组织中的声传播以及诱导产生的生物传热。在高频率、高强度时,非线性波的传播等因素会导致波形失真,非线性效应会产生高次谐波。由于组织对高次谐波的强吸收,非线性方程预测的焦点峰值温度明显高于线性方程预测的焦点峰值温度。因此在浅表组织的仿真中,当换能器频率高、激励声压较大时,HIFU 波的非线性、组织的热黏性的影响不可忽视。缺乏高频FU 声场和温度场的仿真研究导致缺乏对声场非线性和组织热黏性对声场和温度场的影响程度及其规律的认识,这不仅降低了换能器的优化效率,而且导致医生只能依靠个体经验确定输出声功率的范围,难以保证治疗的安全性和有效性,从而限制了高频FU 在其他浅表组织疾病中的推广应用。常见的HIFU 非线性声场仿真模型有Westervelt 方程、KZK 方程[16]、SBE 方程[17]。KZK 方程具有一定的局限性:(1) 未考虑反射和散射的影响;(2) 仅适用于孔径角较小(r<16°)的换能器。由Solovchuk 等[18]的研究可知,当孔径角较小时,Westervelt 方程和KZK 方程两种声学模型的结果近似相等,当孔径角大于16°时,Westervelt 方程和KZK 方程的结果差异较大。SBE 模型虽然适用于孔径角较大的换能器,但是计算方程中个别参数存在经验选择和应用问题[19]。本文使用的换能器孔径角大于30°,因此使用Westervelt方程进行非线性声场的仿真。
针对以上问题,本文基于FU 波的非线性和组织的热黏性,探究临床常用的7 MHz 高频FU 在多层生物组织中的声传播以及毫秒级时间内的生物传热规律,并与线性模型进行了比较。分析了不同输入功率下线性模型和非线性模型之间的差异。同时,分析换能器的参数对组织中声场和温度场的影响。旨在为换能器参数优化及制定安全、有效的高频FU治疗方案提供理论参考。
1 仿真原理
1.1 Westervelt方程
当考虑组织热黏性时,二阶流体黏滞的非线性传播方程,即Westervelt 方程[14,20],可以用来模拟组织中的声场分布:
式(1)中,pt是总声压,t是时间,c是声速,δ为声扩散率(式(2)),ρ是密度。β=1+B/2A为非线性系数(其中B/2A为非线性声参量)。式(2)中,µ为动力黏度,µB为本体黏度,Cp为恒压比热容,γ为比热率,k为导热系数。在式(1)中,前两项为Westervelt线性方程,第三项表示热导率损失和流体黏滞性,最后一项与影响波传播的非线性因素有关。
1.2 Pennes生物传热方程
为了准确预测靶区组织温度场的变化,引入目前最为广泛应用于描述组织在超声作用下的温度场模型—Pennes生物传热方程[21]:
其中,Tt和Tb分别为组织当前温度和血流温度,wb和cb分别为血流灌注率和血液比热容,Q为外部热源。由张平等[22]的仿真结果可知,脂肪组织中血流灌注对HIFU 焦域温度场分布的影响可以忽略不计。但当血管位于焦点时,对焦域温度影响较大。本文主要研究7 MHz 高频FU 在多层生物组织中的声传播以及毫秒级时间内的生物传热规律问题,因此暂未考虑血流对焦点温度的影响。式(3)可以简化为
Q受到两个重要参数的影响,第一个参数是组织的吸收系数,第二个参数是声强。热源可以表示为
其中,αavg和Prms分别为组织的平均吸收系数和声压均方值。ti和tf是积分的开始时间和结束时间。这个区间为声波稳定变化的部分。组织吸收系数与换能器频率为幂律关系,计算公式如下:
式(7)中,f0为基频,α0为基频下组织的吸收系数,f为高次谐波下的频率,b为组织依赖常数,该值介于[0,2]之间。由于吸收系数随换能器频率变化,并且非线性波中会出现高次谐波,因此平均吸收系数可通过以下公式来计算:
式(8)中,αn为第n次谐波下组织吸收系数,εn为谐波幅值与基波幅值之比,该值可从焦点频谱曲线中计算得到。Prms,n和Prms,1分别为第n次谐波下的声压均方值和基频下的声压均方值。通过计算平均吸收系数和均方声压,可以得到任意点的Q值[23-24]。
2 仿真模型及仿真方法
2.1 仿真模型
图1 为基于多层组织建立的声场及温度场仿真模型,由换能器、水域及皮肤、脂肪、肌肉3 层组织构成。本文使用的换能器参数如表1 所示。材料的物理特性如表2[14-15]所示。

表1 换能器参数Table 1 Transducer parameters

表2 材料物理特性Table 2 The physical properties of the materials

图1 多层组织声场仿真模型Fig.1 Multilayer tissue sound field simulation model
2.2 仿真方法
本文使用有限元仿真软件COMSOL 的压力声学瞬态模块及生物传热模块进行仿真,具体仿真过程如下。
本文建立的仿真模型具有轴对称性。因此将组织与换能器同轴排列,模型定义为二维轴对称,可以提高仿真效率。打开仿真软件,在模型向导中选择二维轴对称模型,添加压力声学瞬态和生物传热物理场。在几何工具栏建立换能器以及多层组织的二维轴对称模型,如图2所示。r=0为对称轴,换能器的开口半径为10 mm,曲率半径为12 mm,组织的宽度为10 mm,水、皮肤、脂肪、肌肉的厚度分别为3 mm、1.6 mm、3.4 mm、4 mm[14]。在材料工具栏中添加4 个空材料,根据表2 为多层组织的每一层组织的物理特性赋值。
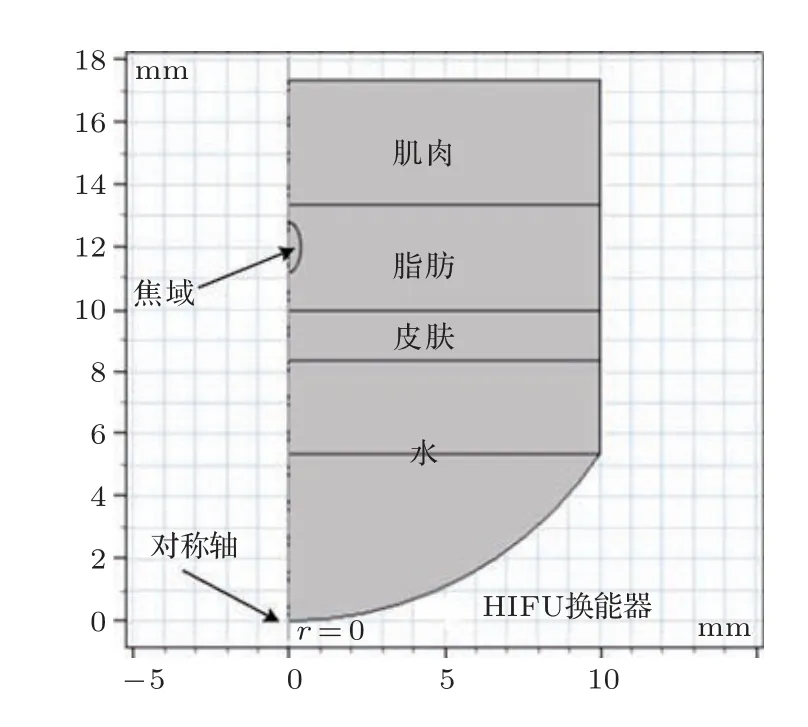
图2 多层组织二维轴对称模型Fig.2 Two-dimensional axisymmetric model of multilayer tissue
为了模拟声波在二维轴对称空间中的传播,需要设置两组边界条件。边界条件定义如下:
(1) 换能器表面声压设为正弦函数如式(10),连续波波形如图3所示。

图3 换能器表面初始激励声压Fig.3 Initial excitation sound pressure on the transducer surface
式(10)中,p0为初始声压,ω=2πf为角频率,f为换能器中心频率。
(2) 设置组织边界为平面波辐射边界条件,假设反射系数和透射系数为零,防止声波的反射。
式(11)中,n为法向量。计算声波传播方程的初始条件为p=0,∂p/∂t=0。计算生物传热的初始条件为T=T0=310 K。
在计算压力分布时,求解波动方程所使用的网格尺寸对仿真精度和计算时间有很大影响。更细的网格可以得到更精确的结果,但是耗时会更长,甚至可能导致解不收敛,因此,在计算过程中选择合适的网格尺寸是很重要的。在COMSOL 多物理场仿真中,最大网格尺寸hmax应满足以下关系:
其中,λw=cL/f为超声波波长,与中心频率f和声速cL有关,N是一个正整数,通常在5∼10 之间。本文中,焦点椭圆区域尺寸设为λw/8,其他区域为λw/6。计算压力分布时,时间步长为1×10-9s,求解声场的时间为15×10-6s;温度场的求解时间为1×10-5s。
在完成建模后,进行时域仿真。利用压力声学瞬态物理场计算压力场,通过求解Westervelt 声波传播方程,可以计算任意位置的瞬时压力。将Westervelt 方程的解的声压均方值代入生物传热模块,与Pennes生物传热方程耦合计算组织中的温度分布,根据式(5)计算Q作为生物热方程中的外部热源,从而得到任意区域的瞬时温度场。
最后,通过改变换能器的参数,如激励声功率(5 W、10 W、15 W)、F 数(0.6 和0.645)、曲率半径(11.2 mm和12 mm)和辐照时间即加热时间(5 ms、10 ms 和20 ms)等,研究各参数对声场和温度场的影响。
参照文献[14,25]的方法来比较不同功率下线性与非线性声压及温度的差异。使用t检验方法,显著性水平为0.05,当p>0.05 时认为线性与非线性模型之间的差别无统计学意义。相反,当p<0.05时说明两种模型之间具有差异,需要考虑非线性效应的影响。
3 仿真结果
3.1 声场计算结果
图4为激励声功率为10 W时,多层组织与水域中x-z平面声场(声压均方值)分布示意图。图5 为多层组织与水域中声压轴向分布示意图。

图4 多层组织与水域中x-z 平面声场分布示意图Fig.4 Acoustic pressure contours (MPa) at the x–z plane (mm) in multi-layer tissue and water
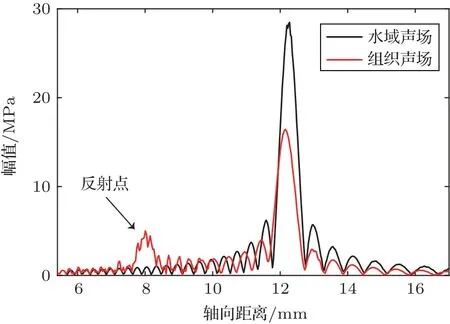
图5 多层组织与水域中声压轴向分布示意图Fig.5 Pressure distribution (MPa) at axial (z)directions (mm) in multilayer tissue and water
由结果可知,在多层组织中大部分声能聚焦在长约0.638 mm、宽约0.2 mm 的椭圆形聚焦区。在皮下脂肪层(焦点区域)声压达到最大值16.4 MPa。通过比较纯水与多层组织中的声场差异,由图5 可知,当声波穿过多层组织时,焦点位置会向换能器方向偏移,在输入声功率为10 W 的条件下,焦点的偏移距离为0.13 mm;其次纯水中焦点声压为28.6 MPa,而多层组织中焦点声压为16.4 MPa,减小了42.657%;由图4 和图5 可知在纯水中声波未发生反射,而声波穿过多层组织时,由于声阻抗差异,会有部分声能量被反射回去,在8 mm 处产生了一个反射点,如图4(a)和图5红色箭头所示。
表3 为不同声功率下线性和非线性模型的正负声压最大值,根据非线性模型和线性模型下的最大声压计算声压增长百分比。

表3 不同输入功率下线性和非线性模型的最大和最小声压(MPa)值Table 3 Maximum and minimum sound pressure (MPa) values for linear and nonlinear models with different input power
由结果可知,在线性模型中,焦点处的波形是对称的,声压最大值和最小值几乎相等。然而,在非线性模型中,随着输入功率的增加,焦点处的波形发生了畸变,声压最大值大于最小值。且随着功率的增加,线性模型和非线性模型的最大声压增长百分比也随之增大。当输入功率低于5 W 时,线性模型和非线性模型的声场分布差异不显著(p>0.05);当输入功率超过5 W 时,声波传播的非线性效应不可忽视(p<0.05)。
图6为输入声功率为0.4 W和10 W 时,在线性和非线性模型中分别绘制的焦点处的声压幅值频谱。表4为非线性模型中,声功率为0.4 W、1.5 W、5 W、10 W、15 W 的n次谐波fn振幅与基波f0振幅的比值。
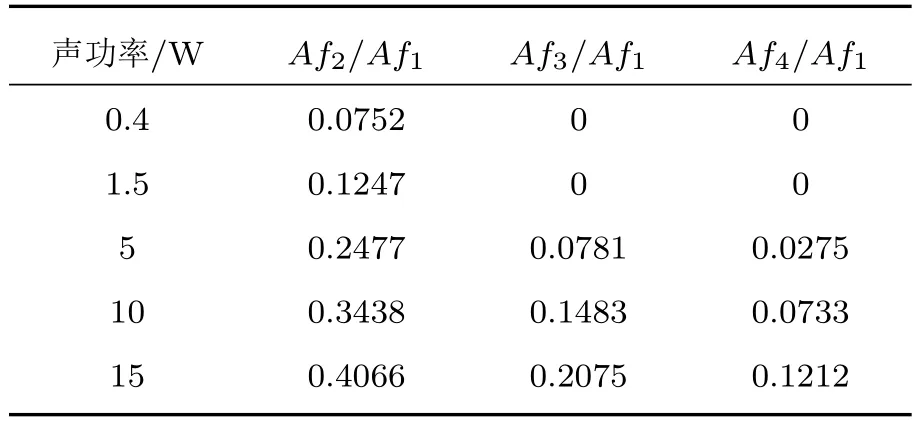
表4 不同声功率时fn 的振幅(A)与f1 的振幅之比Table 4 The ratio of the acoustic pressure amplitude (A) in fn to the amplitude in f1 at different acoustic powers

图6 不同声功率时,线性和非线性模型中焦点处的声压幅值频谱Fig.6 Frequency spectrum of pressure amplitude at focal point in linear and nonlinear models with different sound power
由图6 可知,随着功率的增加,非线性模型中会出现高次谐波,而线性模型中只有基频。由表4可知,随着输入功率的增加,非线性效应更加显著,高次谐波振幅也随之增加,基频能量向高次谐波转移的程度增大。相较于基频,高次谐波的傅里叶系数值相对较小,因此,这里只考虑到4 次谐波的影响。
3.2 温度场计算结果
在计算压力场后,根据公式(3)∼(9)计算温度场。图7 为输入功率为10 W、加热时间为10 ms 时,不同时刻x-z平面温度分布示意图。图8 为轴向和径向的温度分布。
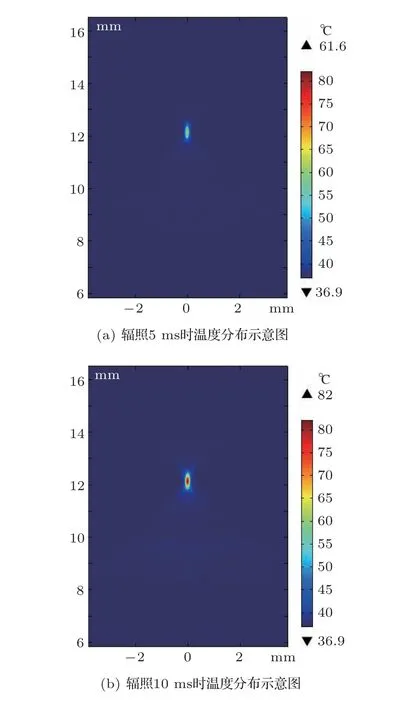
图7 不同时刻x-z 平面温度场分布示意图Fig.7 Diagram of the x-z plane of temperature at different times

图8 焦点处轴向和径向的温度分布Fig.8 temperature distribution (◦C) at axial (z) and radial (r) directions (mm)
由图7 可知,在加热过程中,焦点处的温度不断升高,同时热量不断向周围组织扩散,周围组织温度随之升高,焦域面积不断扩大,在轴向剖面上形成了椭圆形焦斑。在10 ms 时焦点温度达到最大值82◦C。由图5 可知,在8 mm 处有一个较小的声能量,由于水的衰减系数很小,水域区未产生温升,但皮肤的热黏滞性以及皮肤的衰减系数较大,将部分声能量转化为热能,在皮肤层会有一个较小的温升,由图8(a)红色箭头所示。当输入声功率为10 W 时,皮肤层声压为2.244 MPa,温度升高1.51◦C。
表5 为不同声功率下线性和非线性模型的最大温度值,根据非线性模型和线性模型下的最大温度值计算温度增长百分比。
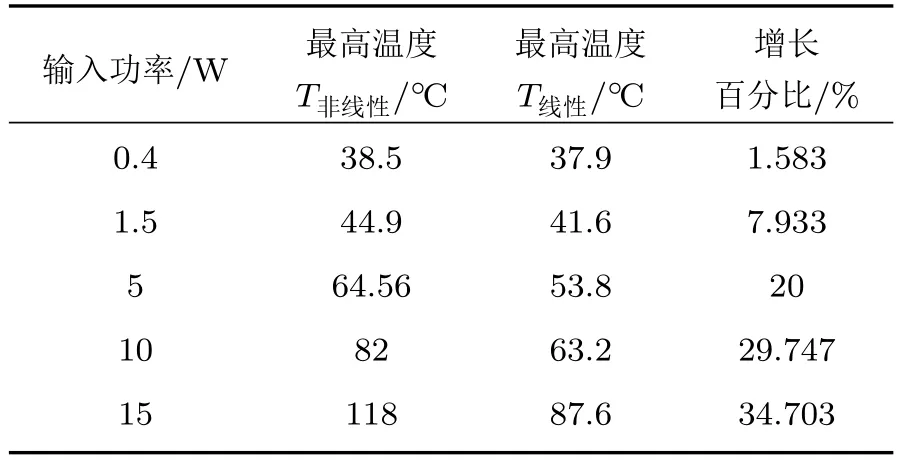
表5 不同输入功率下线性和非线性模型的最高温度(℃)值Table 5 Maximum temperature (◦C) values for linear and nonlinear models with different sound power
由结果可知,非线性模型预测的温度要高于线性模型。线性模型和非线性模型之间的温度增长百分比差随着输入声功率的增大而增大。当输入功率低于5 W 时,线性模型和非线性模型的温度场分布差异不显著(p>0.05);当输入功率超过5 W 时,需要考虑高次谐波对温度造成的影响。
3.3 激励声功率对声场和温度场的影响
为了研究非线性模型中激励声功率对声场和温度场分布的影响,在换能器曲率半径为12 mm、开口直径为20 mm、加热时间为10 ms 时,对5 W、10 W 和15 W三种输入声功率进行了仿真。图9(a)和图9(b)分别为不同声功率下,声压和温度径向分布示意图。
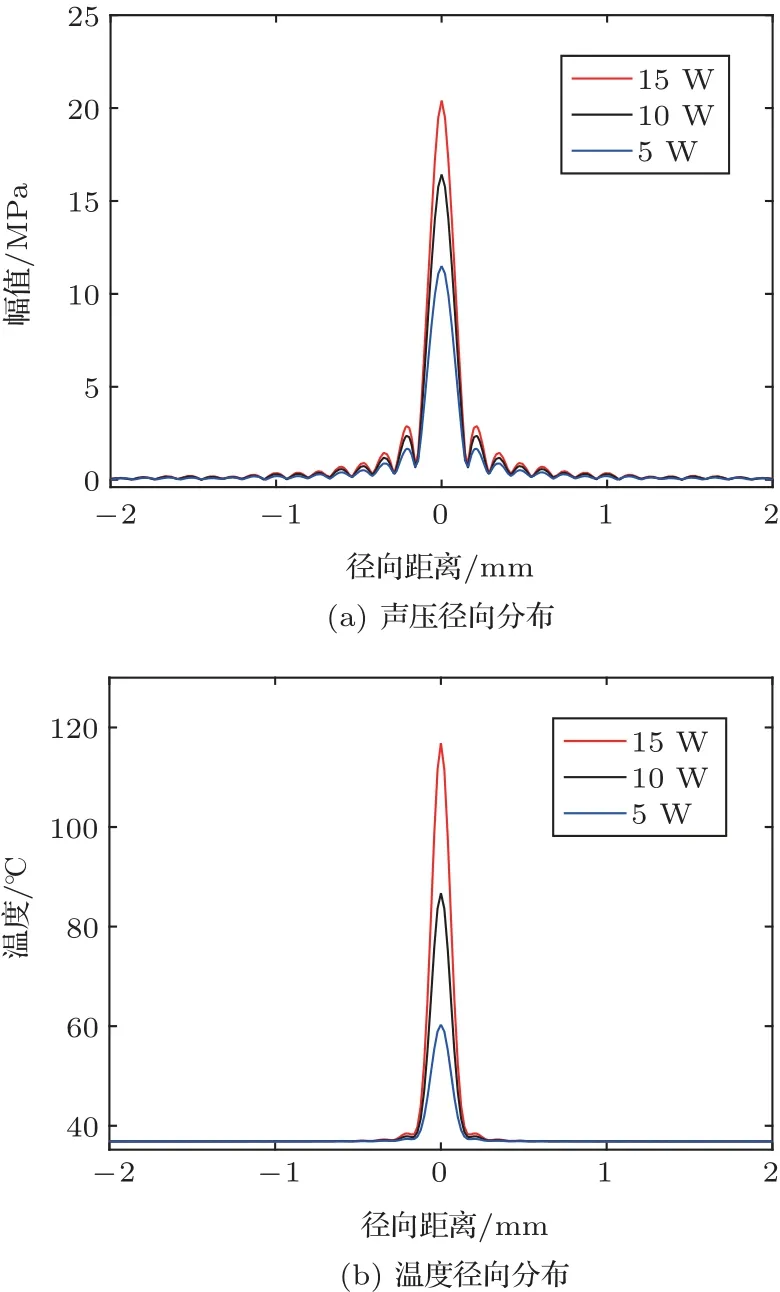
图9 不同声功率时焦点处声压和温度的径向分布Fig.9 Pressure and temperature distribution at radial (r) directions (mm) with different sound power
结果表明,随着输入功率的增加,声波传播的非线性效应更加显著,基频能量向高次谐波转移的程度增大,高次谐波成分更易被组织所吸收,转化为热能。当功率从5 W增大到15 W时,焦点声压和温度分别从10.8 MPa和64.56◦C增大到20.3 MPa和118◦C。由此可见,输入声功率增加,焦点处声压和温度随之变大。
3.4 焦距对声场和温度场的影响
当换能器开口直径为20 mm、激励声功率为10 W、加热时间为10 ms 时,分别在11.2 mm 和12 mm 两个焦距下评估焦距的改变对声场和温度场的影响。径向压力和温度分布如图10 所示。表6为-6 dB 焦域的尺寸。
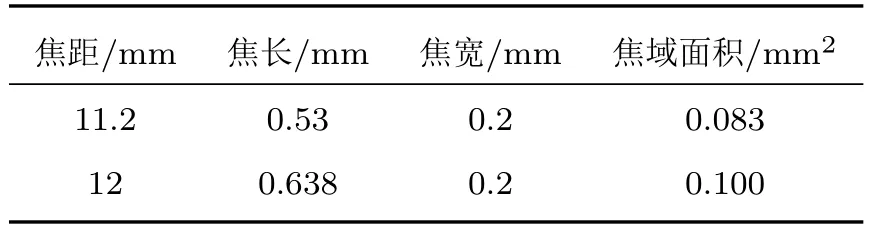
表6 不同焦距下焦域尺寸Table 6 Focal field size at different focal lengths
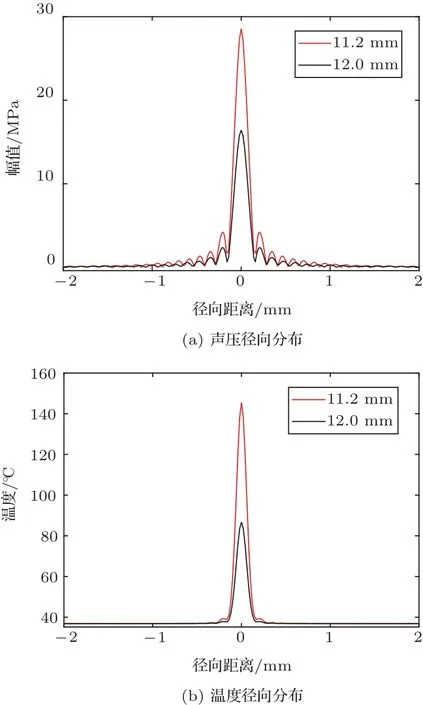
图10 不同焦距时焦点处声压和温度的径向分布Fig.10 Pressure and temperature distribution at radial (r) directions (mm) with different focal length
由结果可知,随着焦距的增大,焦点声压减小,焦域面积逐渐增大,单位面积声能减小,导致焦点处的最高温度减小。在焦距为11.2 mm 和12 mm时,焦长分别为0.53 mm 和0.638 mm。焦点处最大声压达到26.6 MPa 和16.4 MPa,最高温度达到145◦C和82◦C。结果表明焦距增大时,声场和温度场值随之减小。
3.5 F数对声场和温度场的影响
在换能器曲率半径为12 mm、激励声功率为10 W、加热时间为10 ms 时,探究F 数(F 数表示换能器曲率半径与开口直径之比)对声场和温度场的影响。在这一步中,保持焦距不变,改变换能器开口直径。F 数为0.6 和0.652 时,沿径向的压力和温度分布如图11所示。表7为不同F数下焦域尺寸。
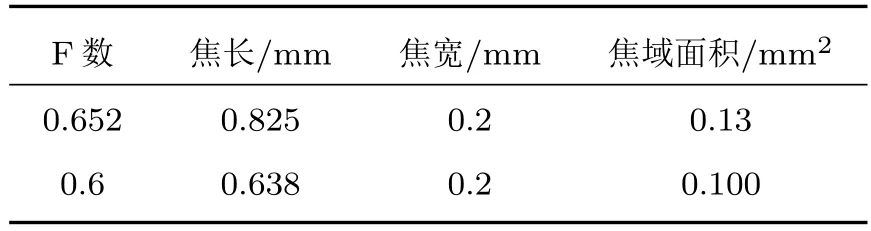
表7 不同F 数下焦域尺寸Table7 Focal field size at different F number
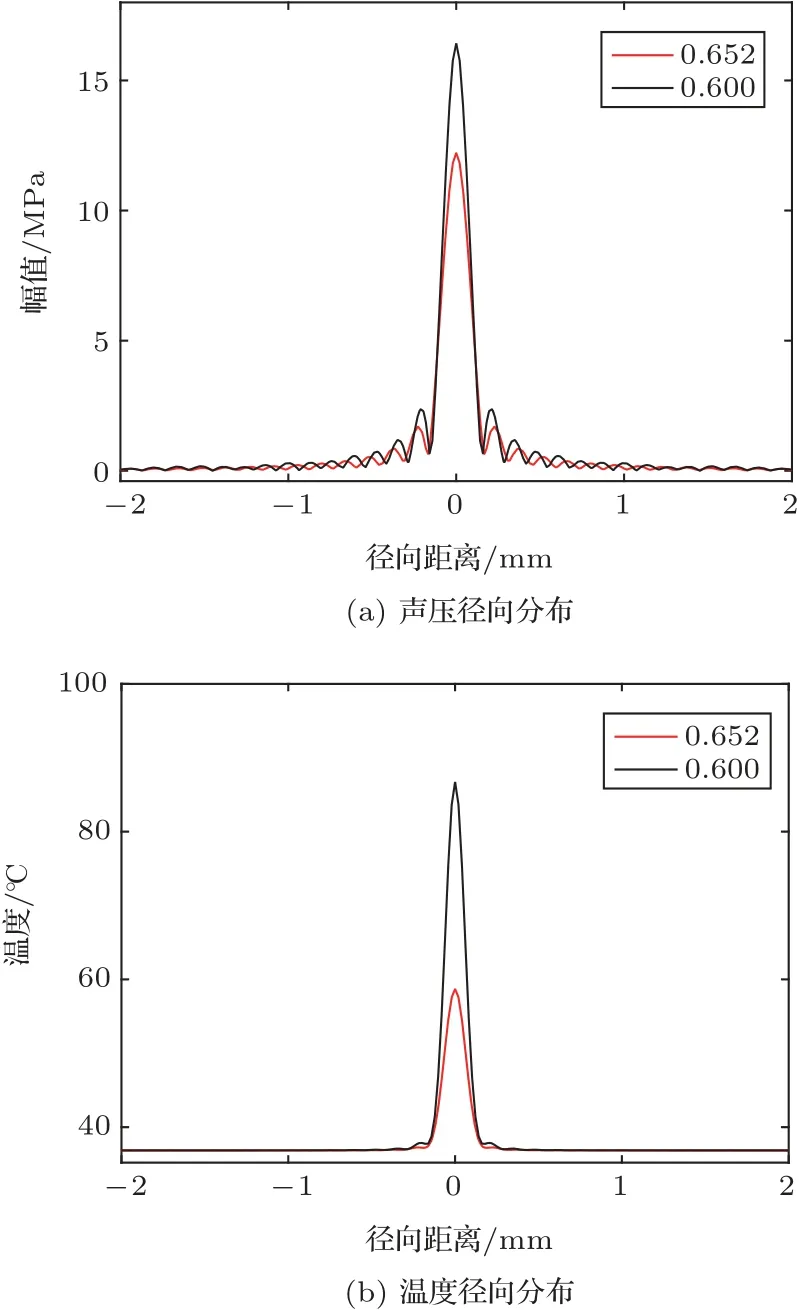
图11 不同F 数时焦点处声压和温度的径向分布Fig.11 Pressure and temperature distribution at radial (r) directions (mm) with different F number
由结果可知,F 数减小时,声压和温度分别从11.6 MPa 和62.1◦C 增加到16.4 MPa 和82◦C。当F数从0.652减小到0.6时,焦长从0.825 mm减小到0.638 mm,焦域面积减小,声能量密度增大,焦点温度升高。
3.6 辐照时间对温度场的影响
在换能器曲率半径为12 mm、开口直径为20 mm、激励声功率为10 W 时,探究辐照时间对温度分布的影响,计算辐照时间为5 ms、10 ms、20 ms时,组织沿轴向的温度分布,结果如图12(a)所示。
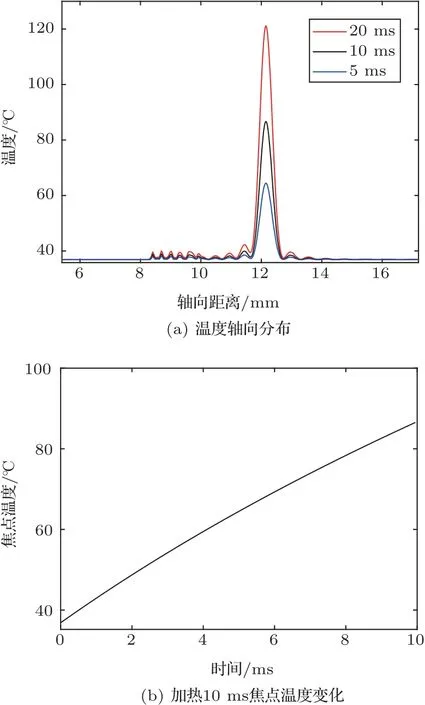
图12 温度轴向分布和焦点温度变化Fig.12 Temperature axial distribution and focal temperature variation
随着辐照时间的增加,3 层组织的最高温度均升高,尤其焦点处的温升最显著,焦点的最高温度分别达到61.6◦C、82◦C 和120◦C。此外,在10 ms 内绘制了组织温升随时间的变化曲线(图12(b))。在激励声功率为10 W 时,随着辐照时间的增加,焦点处的最高温度几乎呈线性增加。
4 讨论
明晰浅表组织内声场和温度场的分布对高频FU 在浅表组织中的应用发展至关重要。对于中心频率为1 MHz 的换能器,Solovchuk等[26]的仿真结果表明,当输入声功率超过112 W 时,非线性效应不可忽视。临床常用治疗肿瘤的换能器中心频率为1 MHz,激励声功率为140∼200 W[27]。在这种工作情况下,非线性效应是不可忽略的。对于4 MHz的换能器,Mortazavi 等[14]使用t 检验方法对线性和非线性模型的声压和温度分布差异进行了分析,结果表明当声强超过8 W/cm2时,需要考虑非线性效应的影响。而对于中心频率为7 MHz 的换能器,并未有研究对其线性与非线性的差异进行讨论。且通过查阅文献发现,考虑到当前临床用于皮肤紧致的7 MHz 换能器的电脉冲能量为0.75∼1.05 J,脉宽为25∼40 ms[11],按照功率型压电陶瓷电声转化效率50%∼60%[28]估计换能器输出的声功率在13∼18 W之间。本文首先对比了线性模型和非线性模型之间的差异,表3 表明当换能器输出声功率大于5 W 时,声波传播的非线性效应就不可忽视;此外,与Mortazavi 等[14]研究4 MHz FU 的非线性效应只需考虑2 次谐波对声场和温度场的影响不同,7 MHz 比4 MHz 超声具有更小的焦点,导致焦点处声传播的非线性效应更加明显,声功率为10 W和15 W 时4 次谐波与基波之比分别达到7.33%和12.12%(表4),因此本文在研究7 MHz FU非线性对温升的影响时,需考虑至4 次谐波对声场和温度场的影响。表5 的结果表明,随着输入功率的增加,声波传播的非线性效应更加显著,基频能量向高次谐波转移的程度增大,高次谐波成分更易被组织所吸收,转化为热能。当声功率从5 W 增大到15 W 时,非线性模型与线性模型预测的温度偏差从20%增加到37.7%。总之,以上结果均表明在非线性模型下探究换能器的参数对声压场和温度场的影响是必要的。
图10 和图11 表明在高频下,微小的换能器的参数变化会显著影响焦点温升,如图10 所示,换能器焦距从12 mm 减小到11.2 mm (减小4%),焦点处的最高温度增加了77%。因此在设计高频FU 换能器时,可以根据本研究提出的模型,调整优化换能器参数,以达到更好的治疗效果。图9 和图12 表明输入参数(声功率、辐照时间)的改变对组织中声场和温度场分布的影响较大,选择合适的参数可以提高治疗效率。因此在治疗的过程中,有必要依据理论仿真选择合适的治疗参数,以提高治疗的安全性和有效性。本文将焦点设在脂肪层,因为脂肪的非线性参数较大,非线性效应更为显著。读者可以根据实际治疗需求调整焦点位置。
本文在仿真过程中发现,声波穿过多层组织时,由于声阻抗差异[29],会有部分声能量被反射回去,在焦点前形成一个反射点,如图4红色箭头所示。由于水的衰减系数很小,水域区未产生温升,但皮肤的热黏滞性以及皮肤的衰减系数较大,在皮肤层会有一个较小温升。通过仿真发现当组织厚度不同时,反射点形成的位置也不同,具体规律将会在接下来的工作中研究。在实际浅表治疗过程中也常出现皮肤灼伤的副作用[30-31],但是靶区的声强必须足够大,才能达到治疗目的。因此可以通过本仿真模型,确定合适治疗参数,在达到治疗目的的前提下,避免皮肤灼伤等副作用的问题。
5 结论
本研究建立了高频FU 辐照多层浅表组织的非线性热黏性声传播及传热模型。首先通过仿真确认了临床使用的7 MHz FU 输出声功率超过5 W时,声波传播的非线性效应不可忽视。其次,非线性声场的频谱分析结果表明,在评估7 MHz FU 的非线性效应对温度的影响时,需要考虑至4 次谐波才能保证温度预测的准确性。最后,在高频下,换能器的参数(激励声功率、F 数、曲率半径和辐照时间)会对声场和温度场分布产生显著影响,为保证FU 治疗的安全性和有效性,在非线性模型下探究换能器的参数对声压场和温度场的影响是必要的。总之,本文提出的多层组织非线性仿真模型与线性模型相比,能够更加准确地预测组织内部的声场和温度场分布,将该模型应用于术前超声治疗剂量方案的制定,将有助于提高FU 治疗的安全性和有效性。与此同时,该模型还为生物医学应用中的高频FU 换能器设计和参数优化提供了一种有用的工具。
本文研究了临床常用的7 MHz高频FU在多层生物组织中的非线性声传播及温升规律,但还存在一些不足:首先,提出的模型未将血流的影响考虑在内,在接下来的工作中将进一步考虑血流灌注对焦点温度的影响,提高模型对温度预测的准确性[32]。其次,本文为提高计算效率使用二维轴对称模型,在接下来的工作中将模型向三维非轴对称转化[33],进一步提高模型仿真三维复杂组织的普适性。

