基于改进最小方差无失真响应角度谱算法的气体泄漏定位方法∗

王天琪 杨祥国 晏 园 刘成龙 张金磊

(武汉理工大学船海与能源动力工程学院 武汉 430063)

0 引言

气体的储存及运输在工业领域应用非常普遍，一旦发生泄漏，就会带来巨大的浪费和能量损失，甚至威胁到人的生命安全[1-2]。因此，对气体泄漏源进行快速准确的定位显得尤为重要。气体泄漏定位是一个广泛的领域，在过去的几十年中得到了深入的研究[3]。基于声学的泄漏源定位方法是通过采集泄漏源释放的超声信号，进而利用声源定位算法定位泄漏源的位置，其中包括时延估计(Time delay estimation,TDE)[4]、机器学习[5]、波束形成[6]和多信号分类算法(Multiple signal classification,MUSIC)[7]等。韦娟等[8]提出的基于模拟信号时域压缩的气体泄漏源波达方向估计算法，通过构造形式相对简单的等效测量矩阵，有效降低了计算复杂度，实现了较高的估计精度。Eret等[9]通过传声器阵列检测泄漏所产生的可听声频段(低于20 kHz)的泄漏声波，利用波束形成方法得到泄漏声源的波达方向(Direction of arrival,DOA)估计，然而在该频段内噪声会将泄漏声源掩盖，导致算法失效。Bian等[10]提出基于声学信号的实时气体泄漏定位方法，该方法使用超声传感器中不同阵元所接收的信号之间的时空域相关性，解决了连续泄漏超声信号的实时定向问题。Yan 等[11]提出一种将声发射(Acoustic emission,AE)传感器结合MUSIC算法和小波数据包分析的新方法，对大型压力容器上多个泄漏源的定位进行了实验研究，具有良好的定位多个泄漏源的潜力。基于角度谱[12-13]的声源测向方法适用于噪声环境下的声源DOA 估计。Blandin 等[13]提出了一种基于最小方差无失真响应(Minimum variance distortionless response,MVDR)的角度谱定位算法，实现了声源的准确定位，但该方法在进行高频声源定位时获得的聚合角度谱中因空间混叠及其他实际因素影响，容易导致较多的漏警和虚警。

针对上述问题，本文利用泄漏信号的超声特性，通过引入信噪比(Signal noise ratio,SNR)追踪加权和基于时频稀疏性的分频带处理的方式，提出基于改进MVDR角度谱算法的气体泄漏定位方法，以期在复杂的噪声环境中提升气体泄漏定位的精度，增强工程的实用性。

1 MVDR角度谱方法原理

假设空间中有N个泄漏源信号，由M个阵元所组成的超声传声器阵列所接收到的泄漏声学信号可表示为

式(1)中，xm(t,f,τ) (m=1,2,···,M)表示第m个传声器阵元对应的观察信号，sn(t,f) (n=1,2,···,N)表示第n个目标泄漏源的声学信号；n(t,f)表示接收信号中包含混响和噪声部分的加性复合噪声；A(f,τ)=[a1(f,τ1),a2(f,τ2),···,an(f,τn)]是所有声源信号到传声器阵列之间的传播模型矩阵，an(f,τn)表示与第n个源对应的导向矢量：

式(2)中，τn为所求声源到传声器两个阵元间的到达时间差。

MVDR 波束形成是一种自适应波束形成算法，旨在使用转向矢量对空间内所有方位角进行“扫描”，通过调整权值矢量使得在能量一定的前提下的输出信号最大[14]。加权后的输出响应可表示为

式(3)中，WH=[w1,w2,···,wm(t,f)]T为权值向量。

假设信号与噪声干扰不相关，将式(1)代入式(3)：

根据式(4)可以得到声源信号与噪声信号的功率，如下所示：

式(6)中，w(·)是局域二维窗函数，本文采用的是海明窗。

根据式(6)可以得出作MVDR 波束形成后，各个方向的期望信号能量：

聚合角度谱的时频域角度谱函数：

所有网格点内的函数ϕMVDR(t,f,τ)在时频域上积累较大的值：

2 改进算法的构建

2.1 SNR追踪加权

由于噪声不可避免，声源数较多的混响环境下，会导致MVDR 波束形成器在抑制干扰信号的同时削减期望信号，降低定位精度。本文提出一种基于Softplus 函数的SNR 追踪加权方式，首先根据每个时间帧某一阵元接收信号的频域协方差矩阵估计SNR，通过SNR追踪提取受噪声影响较小且单个声源能量占优的时频支撑域，进而通过Softplus 激活函数自适应的调整不同SNR 下气体泄漏信号的频域分量对期望信号能量P(t,f,τ)的贡献，在充满低频噪声的环境中增加气体泄漏信号超声频段的频谱权重，达到抑制加性复合噪声的目的。

超声传声器阵列的SNR输出可表示为

假设噪声稳定不变且前L段为纯噪声，则有

结合泄漏源所在环境给出经验阈值µs，若该时频支撑域的χSNR高于给定阈值，则被认为包含一个主导声源，从而得到满足局部SNR追踪的时频支撑域集合为

提取受环境噪声影响较小的时频域集合ΩSNR(t,f,τ)，进而获得满足泄漏能量占优的时频域参与角度谱函数的累加。

本文采取Softplus 激活函数，Softplus 函数其理论表达式为ln(1+ex)，利用此函数对x求微分，Softplus 函数的导函数是1/(1+e-x)，可以看出该函数是一种非线性连续可微函数，其变化平缓且光滑，收敛速度相对较快，不会出现强制的稀疏处理而屏蔽一部分的有效特征。利用该函数将SNRχSNR映射为每个频点的加权值，即

将加权值G(t,f,τ)用于角度谱函数的计算，以调整不同SNR的频域分量对角度谱函数的贡献，加权后的角度谱函数中泄漏信号SNR 低的频率权重小，而SNR高的频率权重大。

2.2 基于时频稀疏性的分频带处理

声学信号的时频稀疏性，即W-DO 特性，一般指将时域观察声学信号经由短时傅里叶变换(Short time Fourier transform,STFT)到时频域信号后，各个声源的能量只分布在占比很小的时频支撑域中，不同的声源间的声学信号时频成分几乎是完全错开的，每个时频点上仅有一个声源占优[15-16]。利用声学信号的时频稀疏性，可将整个频域内的多声源定位问题转化为局部频带内的单声源定位问题。

将式(1)声学信号经过STFT 后可表示为如下数学模型：

其中，Am,n(f,τ)包含直达波与混响成分，反射波的强度均匀分布于所有可能的传播方向上，此时传递函数Am,n(f,τ)中的混响成分可以看作空间散布的噪声，故可分解为直达波成分(f,τ)及混响成分(f,τ)两部分的求和，即：

当满足时频稀疏特性时，且仅考虑直达波成分：

其中，αm,n和im,n/fs分别表示第n个声源与第m个传声器阵元之间传递函数中与直达波成分相对应的传播衰减系数和传播时间。

设泄漏源定位时的频率范围设置在[fL,fH]之间，由空域奈奎斯特采样定理，可得最大不模糊频率：

为了避免高频混叠现象，将频带划分为[fL,fc]与[fc,fH]两个子区间。当fH>2fc时，[fc,fH]又可分为[fc,2fc]和[2fc,fH]两个部分，那么根据

式(18)中，U(·)为向上取整运算符，将整个频带划分为[fL,fc],[fc,2fc],···,[(P-1)fc,fH]。此时结合式(8)中MVDR 角度谱函数的定义式，可得单个子频带内的局部角度谱函数：

基于声学泄漏信号的时频稀疏特性，利用频率区间划分的方式计算局部角度谱函数，通过时频域累积产生角度谱函数时，抑制由低频段能量的积累造成的噪声源过估计，而且可以有效避免高频混叠现象。

2.3 改进后的MVDR角度谱算法

式(19)中仅包含单个子频带内单个声源的位置信息，为了准确获得整个频带内所有声源的位置信息，将2.1 节中所提到的SNR 追踪加权运用到经分频带处理的局部角度谱算法中，增加高SNR的子频带角度谱函数权重，即增加泄漏声源的有效权重。通过加权值G(t,f,τ)与局部角度谱函数ϕMVDR联乘，并对所有子频带的局部角度谱函数进行累加，即可得到整个时频域的角度谱函数：

式(20)中，NpH与NpL分别表示最高频率与最低频率在子频带中所对应的序号。

综上所述，本文算法的相应处理步骤归纳为如下：

步骤1 将传声器阵列收集到的声学信号做STFT，得到离散时频域的表达式为xm；

步骤2 由式(10)通过SNR 追踪求得各个时频域的SNRχSNR，通过式(12) 提取受噪声影响较小的时频域集合ΩSNR；

步骤3 根据式(18)将时频域集合ΩSNR划分为不存在高频混叠现象的P个子频带，并由式(19)求得各个离散频带的局部角度谱函数ϕMVDR；

步骤4 将每个子频带的加权值G(t,f,τ)与局部角度谱函数ϕMVDR联乘，并将所有子频带的局部角度谱函数累加求和，得到ΦMVDR，再通过式(9)求得即为估计的泄漏源位置。

3 数值仿真及分析

为了验证算法性能的优越性，利用仿真实验平台，参考文献[17]，将气体泄漏声源的检测频段设为0∼48 kHz。设置传声器阵列为直径0.1 m 的均匀圆阵，阵元个数为16，方位角与俯仰角的角度搜索范围均为(0◦∼180◦)。在计算机仿真环境中，分析本文算法、传统MVDR 角度谱算法和MUSIC算法的有效性，并对比在不同SNR和不同采样点数下的定位性能。

3.1 算法有效性分析

设置泄漏源数N=1，采样点数1024 个，泄漏源SNR 设为10 dB，泄漏源方向角和俯仰角分别为φ=75.00◦、θ=20.00◦。其仿真结果如图1所示。

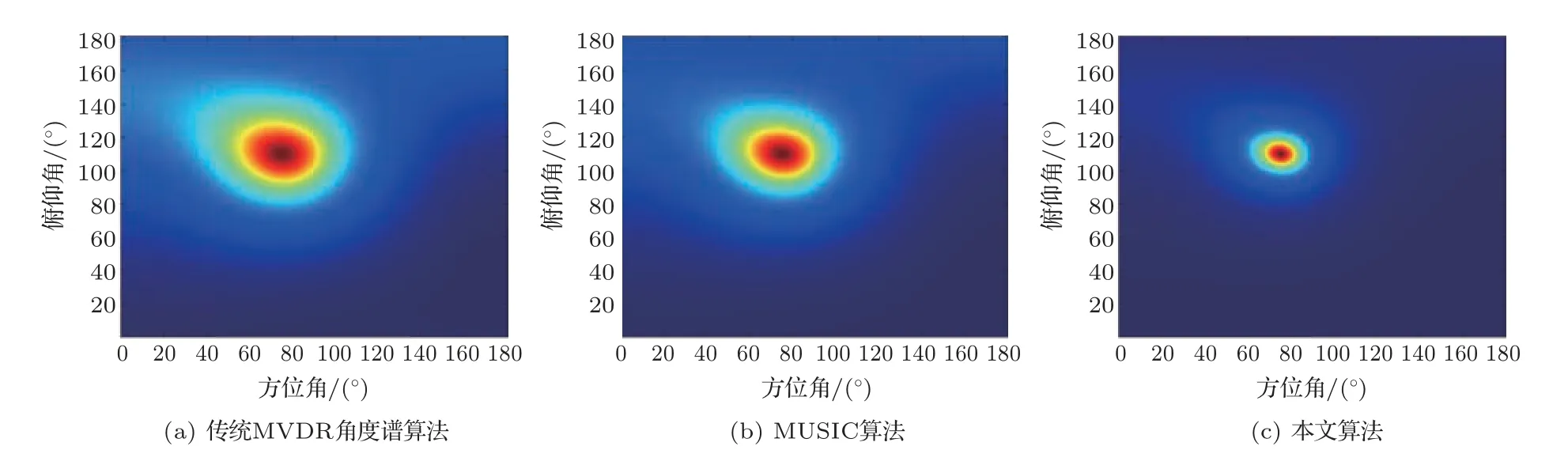
图1 泄漏源定位仿真结果Fig.1 Leak source location simulation results

仿真定位结果显示3 种方法均能对泄漏源进行定位。通过3 种算法的结果图对比，可以看出传统MVDR角度谱算法的主瓣宽度较宽，且抑制旁瓣效果较差(图1(a))；MUSIC 算法相较传统MVDR 角度谱算法略有优化(图1(b))；本文算法成像结果的主瓣宽度变窄，旁瓣的能量幅值降低(图1(c))，仿真结果显示本文方法对噪声的鲁棒性更强，削弱了由混响造成的旁瓣，抑制了低频噪声信号的能量积累，增加了泄漏声源的时频域权重，表明定位算法的抗干扰能力得到进一步提升。

不同方位的DOA估计性能如表1 所示。由表1可以看出，在条件相同的环境下，本文算法、传统MVDR 角度谱算法和MUSIC 算法都能进行有效的DOA 估计，但本文算法与预设结果偏差较小，改进后的MVDR 角度谱算法的DOA 估计精度得到了很大的提高。方向角的平均定位误差约为0.60◦，俯仰角的平均定位误差约为0.62◦，相较于其他两种算法，本文算法在相同条件下的稳定性明显提高。

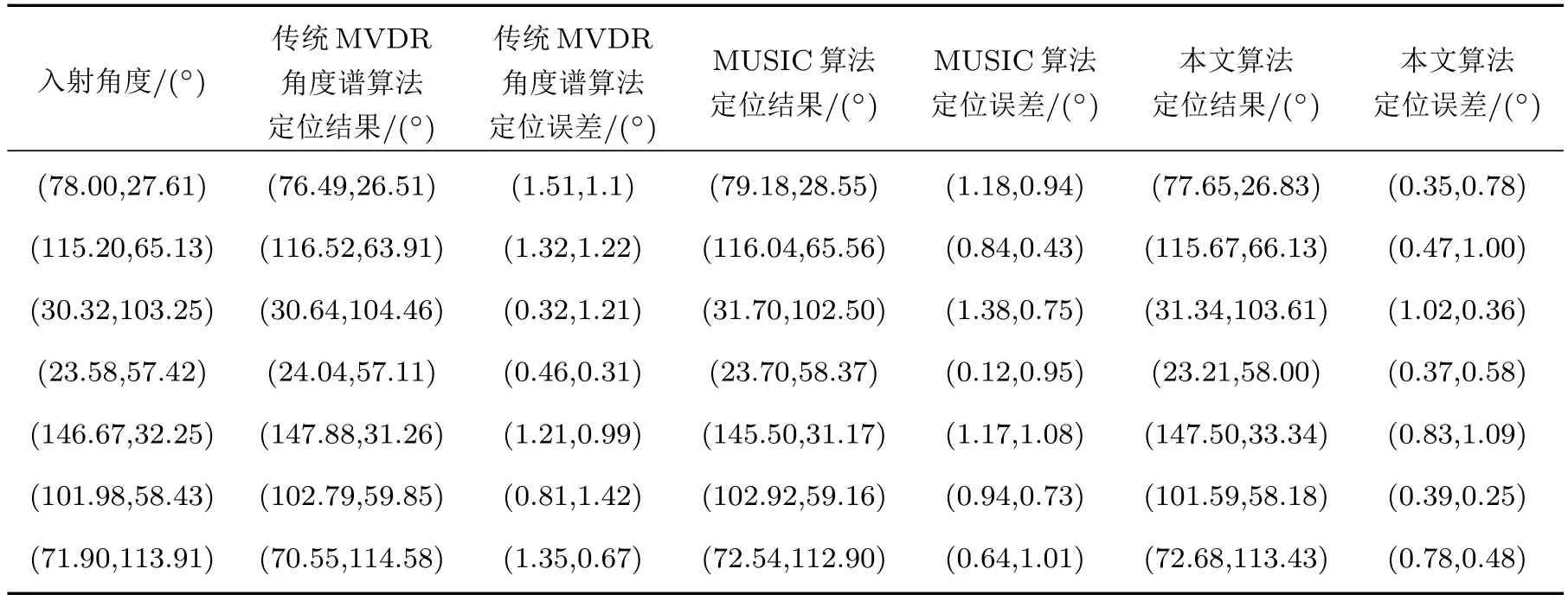
表1 不同方位的泄漏源定位仿真性能Table 1 Simulation performance of leak source location in different directions

3.2 算法定位性能分析

为进一步验证本文算法性能优势，保证其他参数不变，比较在不同SNR 和采样点数情况下3 种算法的定位性能。为评价算法性能，本文选择均方根误差(Root mean square error,RMSE)作为评价标准。

3.2.1 SNR对算法性能影响

将声学泄漏信号的采样点数设置为1024次，使SNR 从0∼20 dB 以间隔5 dB 变化，对3 种算法分别进行多次实验。图2 给出了不同算法的RMSE 随SNR变化的曲线图。

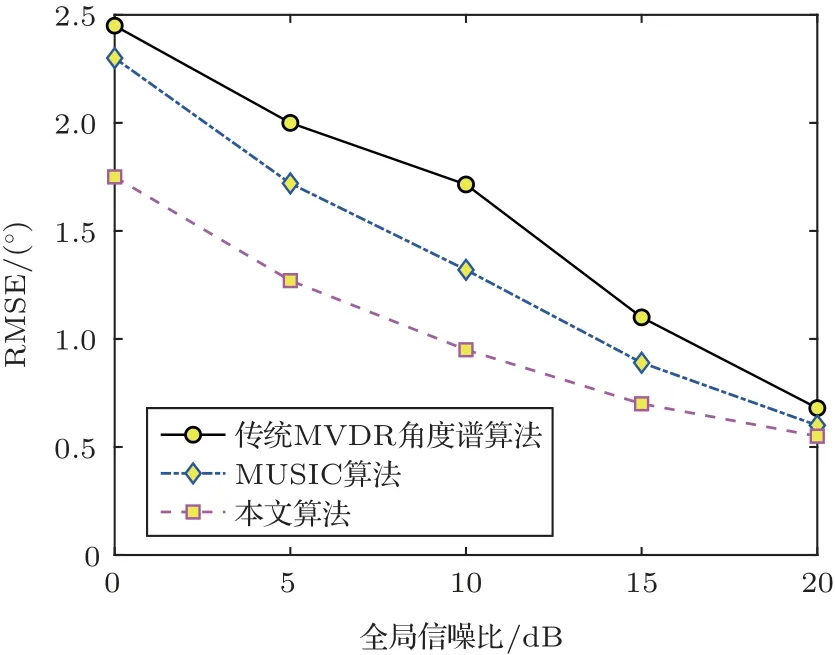
图2 算法RMSE 与SNR 关系Fig.2 Relation between algorithm RMSE and SNR

根据图2 结果可知，在不同SNR 环境下，传统MVDR 角度谱算法、MUSIC 算法和本文算法均能进行泄漏源定位，但本文方法的RMSE 均优于传统MVDR 角度谱算法与MUSIC 算法，尤其在中低SNR 环境中，本文算法的定位RMSE 相较于其他算法提升明显，说明该算法在低SNR 环境中的适应性较强，定位效果得到明显改善，符合算法设计初衷。

3.2.2 采样数对算法性能影响

将声学泄漏信号的SNR 设置为10 dB 不变，使采样点数从100∼1000 次以间隔100 变化，对3 种算法分别进行多次实验。图3 给出了不同算法的RMSE随采样点数变化的曲线图。

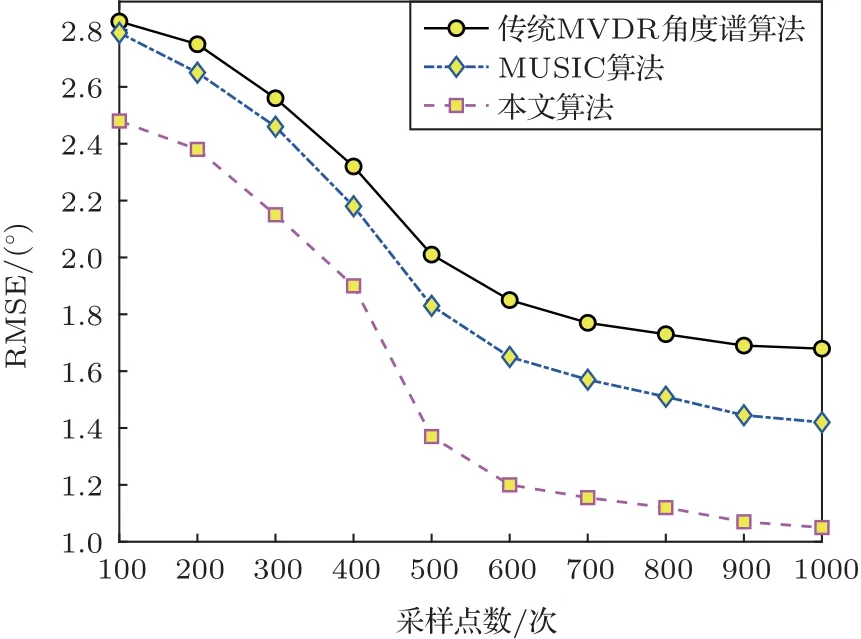
图3 算法RMSE 与采样点数关系Fig.3 Relation between algorithm RMSE and sampling points

由图3 仿真结果可知：当采样点数不同时，3 种算法都能进行有效定位，本文算法在低采样点数下可以更好地识别出真实泄漏源位置。在相同采样点数下，本文算法RMSE 均小于传统MVDR 角度谱算法和最大可控响应功率波束形成法算法的RMSE，整体优于其他两种算法，由此可见本文算法在搜索目标泄漏源时具有成功率高、稳定性强等优势，体现出了很好的定位性能。

综上所述，在采样数较少和SNR 较低的情况下，引入SNR追踪加权和基于时频稀疏性分频带处理的MVDR 角度谱算法可以获得较为满意的定位精度，进而说明其DOA估计性能的优越性。

4 实验验证

4.1 实验设置

为了保证算法在工程应用中的可行性，验证本文算法的有效性和正确性，建立气体泄漏源定位系统，如图4所示。定位系统由空气压缩机、计算机、超声传声器阵列及摄像头组成。

图4 气体泄漏源定位系统Fig.4 Gas leak source location system

文中研究对象为压力气体泄漏源，为了模拟出实际的泄漏源，选用了型号为QTX1500X2 的空气压缩机，它可以提供7 bar 的泄漏压力，装配一个0.5 mm的喷嘴作为泄漏孔，用于模拟气体泄漏产生声波信号。为保证最佳响应，实验中选用16个型号为SPH0641LU4H-1 压电式超声传声器组成传声器圆形阵列，用以采集泄漏源产生的超声信号，该传感器的采样频率为96 kHz，灵敏度为-26 dBFS，尺寸为8 mm×7.5 mm，具有优秀的宽带声频性能和射频抗干扰性能。同时利用声场可视化技术[18]，通过摄像头标定，建立声源空间坐标与图像像素点之间的映射关系，将空间位置的声功率图与摄像头拍摄的实景图像融合后进行显示，形成气体泄漏信号可视化图，用以观测算法估计位置与实际泄漏点的一致性。

实验是在一个7 m×4 m×4 m 的混响室中进行的，噪声为空间白噪声及信号发生器模拟噪声。在实际的气体泄漏定位实验中，首先采用上述的传声器阵列采集由模拟泄漏源产生的泄漏超声信号，然后再通过本文定位算法对泄漏源进行方位估计。实验前保持空压机喷嘴和超声传声器阵列在同一高度上，实验过程中通过改变两者之间的相对位置来模拟不同角度下的泄漏源。

4.2 实验结果

利用本文算法分别对不同位置、不同SNR以及不同采样点数下的实际气体泄漏进行定位。本节设计的实验工况及定位结果如表2 所示。以不同位置泄漏中心坐标为基准，可得本文算法的不同工况下平均方位角定位误差分别为0.95◦，平均俯仰角定位误差0.87◦，总误差始终小于3.5◦，说明该算法稳定性高且估计效果较好。

表2 实验工况及定位结果Table 2 Experimental conditions and positioning results

取工况1、工况6、工况7、工况9 为例具体分析，由超声传声器阵列第一个阵元所接收到原始信号的时域图及频谱图依次如图5 所示。从图5(a)中可以看出，阵元与泄漏源的位置及SNR变化导致时域信号的幅值存在差异。从图5(b)中可以看出，空压机所模拟出的气体泄漏信号为宽频信号，包含了多个频率成分，但采集到的泄漏信号中能量主要分布在超声频段内，证实了分频带处理抑制低频噪声的有效性。

图5 泄漏信号的时域与频谱Fig.5 Time domain diagram and spectrum diagram of leakage signal

对于工况1、工况6、工况7、工况9，通过改进MVDR 角度谱算法得到气体泄漏源的定位结果如图6 所示，搜索由方位角与俯仰角组成的整个二维平面，其中角度谱函数输出功率的谱峰位置即为泄漏源的位置，由图6(a)、图6(c)可知，在SNR 较大且采样点数较多时，算法受噪声影响较小，能够精准定位泄漏源位置。由图6(b)、图6(d)可知，在SNR较小且采样点数较少的情况下，本文算法均能进行有效的定位，具有较强的鲁棒性。气体泄漏可视化图如图7 所示，根据可视化图可以观察到泄漏源空间位置与算法定位位置保持一致，超声传声器阵列采集的实验数据经过本文算法计算可以较为准确估计气体泄漏位置，证实了本文算法在实际工程应用中的可行性。

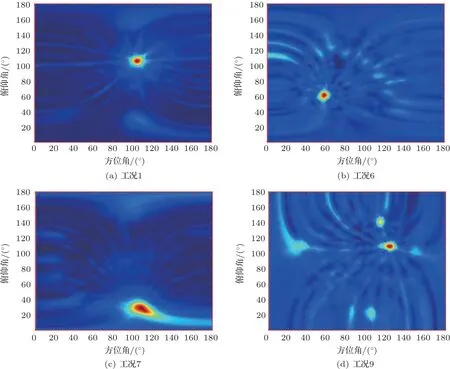
图6 气体泄漏定位结果Fig.6 Gas leak location results

图7 气体泄漏可视化图Fig.7 Gas leakage visualization

5 结论

本文针对在现有算法在噪声环境中难以准确定位微小气体泄漏的问题，根据气体泄漏声源的时频域特性，提出了一种基于改进MVDR角度谱算法的气体泄漏定位方法，得到了以下结论：

(1) 本文在传统MVDR 角度谱算法的基础上引入SNR 追踪加权和基于时频稀疏性的分频带处理，提取受噪声影响较小且单个声源能量占优的时频支撑域，自适应地调整不同频率分量对角度谱函数的贡献，并且可以抑制低频段能量的积累而造成的低频噪声源过估计，避免高频混叠现象的产生。

(2) 仿真实验验证了在不同方位、不同SNR 以及不同采样点数的情况下，对比传统MVDR角度谱算法和MUSIC 算法，本文算法均能保证更精确稳健的定位性能。

(3) 实验环境下对不同工况的气体泄漏源进行定位均可以得到较为准确的结果，且总定位误差始终小于3.5◦。证明了本文算法在实际工程应用中的准确性与有效性。