波束开角对多普勒测频结果的影响∗

陈 茁 王长红 邓 锴

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

(3 北京市海洋声学装备工程技术研究中心 北京 100190)

0 引言

多普勒测速声呐广泛应用于水文测验、海洋监测、环境保护等领域。多普勒测速原理基于多普勒效应，对于存在相对运动的声源和接收点，接收的回波信号将引入多普勒频移，测频偏差是测速偏差的主要来源之一。已有信号机理方面的偏差分析文献大多基于单质点回波模型，从相位编码信号的特性出发，研究填充系数、编码长度等对测频偏差的影响。如黎美琪等[1-2]证明了单质点回波模型下测频偏差与宽带信号频谱特性有关，主要聚焦发射信号频谱不对称的影响，利用差分Blackman 码调制发射编码信号有效降低了测频偏差。对水底椭圆散射模型主要是开展模型准确度和回波信号特性研究，刘德铸[3]提出了利用水底椭圆散射模型构造回波信号，通过仿真和典型试验数据瞬时值与包络值的频数统计函数的相似性证明了模型的准确，未分析模型对回波信号频谱结构的影响。黄雄飞等[4]推导了水底回波信号自相关函数的表达式，其形状与发射信号自相关函数基本一致，但相对发射信号有一定的展宽或压缩，缺少该模型对回波信号测速性能的影响研究。

本文在上述文献基础上，基于水底椭圆散射模型，分析了声学宽带测速底回波信号的频谱特性，以及声学波束开角对宽带回波信号测频性能的影响，得到了波束开角对测频偏差的影响机理，对宽带声学多普勒测速偏差研究具有重要价值。

1 波束开角对测频偏差产生影响的原因

现有的多普勒声呐水底回波研究模型分为两种：单质点回波模型和椭圆回波模型，由于单质点回波模型是一种理想化模型，忽略了波束开角，难以反映回波信号幅度变化细节，本文以水底椭圆散射模型为基础进行分析。具有一定波束开角的波束照射在水底，水底投影近似看作椭圆，散射点均匀分布在椭圆平面，将椭圆划分为2K+1 个条带区域，K为正整数，区域间隔与波长成比例。波束到达水底的垂直深度H、波束宽度Ψ、波束入射角θ均为已知量，椭圆长轴与x轴的夹角为0◦，椭圆的几何中心x0、波束中心与椭圆交点、长轴a和短轴b可由已知量计算，水底散射点分布和条带划分如图1 所示[4-5]。

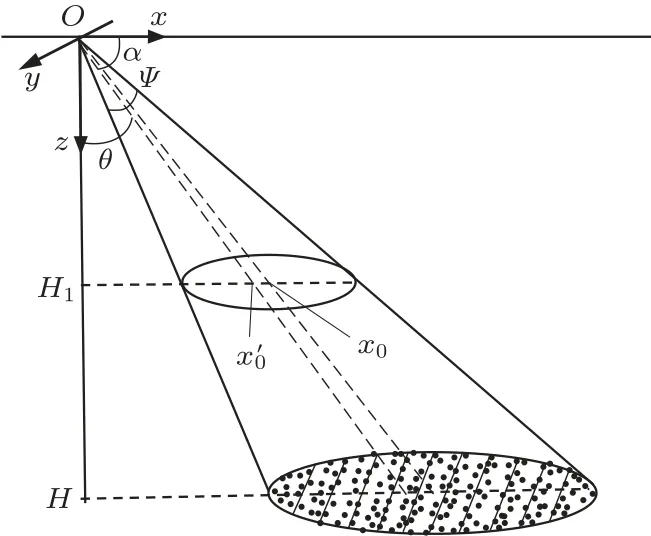
图1 水底照射条带划分示意图Fig.1 Diagram of underwater irradiation strip division

单质点回波模型下，频谱的伸缩仅与波束轴线方向的多普勒频移fd有关，在水底椭圆回波模型下，频移不是固定值，存在一定范围的频率扩展。黎美琪[2]提出宽带信号可等效为单频点信号的幅度加权叠加，信号幅值受到环境因素的影响，与倾角θ和频率f有关，接收信号由所有条带区域对应的宽带回波信号叠加得到

其中，k表示椭圆不同的条带区域，i表示宽带信号不同的谱线。不同深度、波束开角得到的椭圆模型具有不同的中心位置和面积。各条带区域对应的多普勒频移fdk与波束方位有关fdk=fdsinθk/sinθ，θk为不同条带区域位置向量(xk,0,zk)与z轴正向夹角。

发射的重复编码信号频点幅值[6]计算方法见式(2)：

其中，Tb为码元宽度，zn为宽带信号编码序列，R为编码重复次数，T为信号长度，∆f=f0/(QL)为谱线间距，Q为填充系数，L为编码长度。接收信号的幅值加权A(θ,f)主要由两部分组成，方位对频点的加权和吸收对频点的加权[7]。

综上所述，

水底椭圆散射模型下不同条带区域扩展损失、散射强度不同，扩展损失随着掠射角减小而增大，散射强度随着掠射角减小而减小，波束开角越大，不同方位二者差异越大，频谱不对称程度越强，影响测频偏差增大。接收回波信号表达式为

幅值的具体表示见式(4)、式(5)：

2 波束开角对测频偏差的影响分析

2.1 波束开角对频谱结构的影响

从本文给出的接收回波信号幅度表达式可知，方位对频点的加权随着掠射角减小而减小，吸收对频点的加权随着频率的增大而减小，二者共同作用导致回波信号频谱幅值不对称。

图2 中原图表示接收的宽带信号谱线，局部放大图表示各谱线由椭圆条带区域窄带信号叠加得到，频谱中心f0+fdk与f0+fd0的左右谱线幅度均存在差异，二者右侧谱线幅度低于左侧幅度直观地讲，回波信号频谱中心的左右谱线幅度存在差异，将会造成左右频谱的能量存在差别，故可以左右频谱的能量差衡量频谱不对称的程度。设衡量频谱不对称的两个系数分别为方位不对称系数εθ和吸收不对称系数εf。

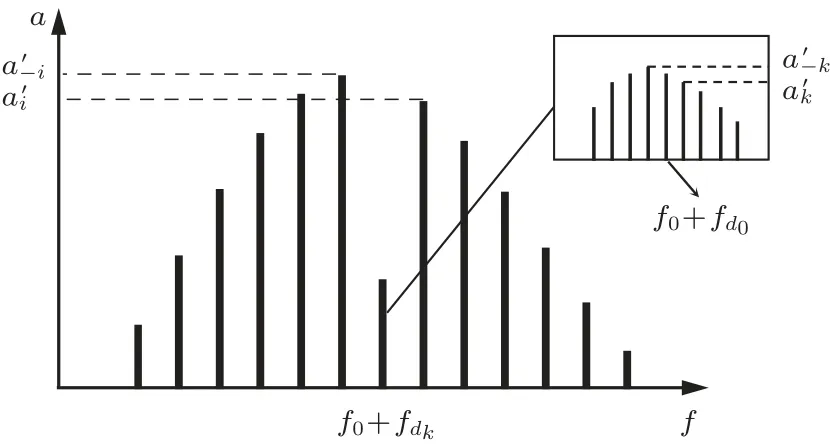
图2 回波信号不对称频谱示意图Fig.2 Diagram of asymmetrical spectrum of signal

其中，方位、吸收对频点的加权经过归一化，K和I表示单侧对称频谱总能量。选取中心频率f0=150 kHz，采样频率fs=10f0，编码信号长度L=13，填充系数Q=6，编码重复次数R=24，水深110 m，波束入射角20◦，散射点间隔为0.05 m，条带间隔为0.1 m，利用式(4)和式(5)计算吸收损失、散射强度等因素对信号幅度的影响，多普勒频移120 Hz，在波束开角范围[2◦,20◦]仿真波束开角与不对称系数的关系。

图3 中三角线代表吸收不对称系数，星形线代表方位不对称系数，不对称系数为负值表示频谱右侧能量少于左侧，测频偏差为负值。波束倾斜照射在水底，增大波束开角，足印随之增大，足印左右两侧传播距离与掠射角差异逐渐增大，对吸收不对称系数没有影响，方位不对称系数增大，频谱不对称程度增强，测频偏差增大。

图3 波束开角对不对称系数的影响Fig.3 Influence of beam angle on asymmetry coefficient

2.2 波束开角对测频偏差的影响

根据复自相关频率估计算法[9-10]，多普勒频移估计表达式

从式(8)可知，估计多普勒频移需对复合信号求复相关，由于接收信号为实信号，经过正交解调滤波后得到复合信号，回波信号处理流程如图4所示。

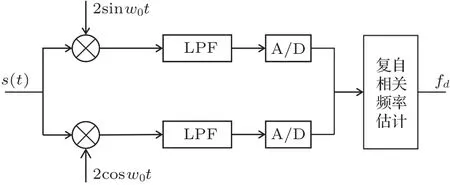
图4 宽带回波信号处理框图Fig.4 Diagram of broadband echo signal processing

复合信号表示为

其中，∆frk=∆f(1+fdk/f0)。对复合信号求相关函数

其中，k为条带区域编号，从左到右分别为[-K,K]，k<0时，u(k)=1，k≥0 时，u(k)=0，后续表达式中用Dk代替波束中轴线与椭圆平面的交点横坐标sx0表示为sx0=htanθ，椭圆中心条带位置横坐标x0表示为

设中心条带轴线与波束中轴线的夹角为θ0，中心条带左侧、右侧相邻区域轴线与波束轴线夹角分别为θ-1、θ1。以θ0为例，根据椭圆模型几何关系可列出如下表达式：

化简整理得到θ0≈tanθtan2(Ψ/2)，同理可得

fd0为中心条带对应的多普勒频移，将θ0≈tanθtan2(Ψ/2)代入频移三角函数形式，化简可得fd0=fd+fdtan2(Ψ/2)。∆-1、∆1分别表示中心条带与左侧、右侧相邻条带区域多普勒频移差值：

d=∆1-∆-1模拟各区域多普勒频移差值非线性变化：

给定入射角、波束开角和条带数目可计算不同条带对应的多普勒频移。将频移表达式(11)代入式(10)，相关函数化简可得

相关函数的实部为

相关函数的虚部为

由于式(21)、式(22)后一项比前一项低3 个数量级，故相关函数可进一步简化为

当波束宽度较小时，波束中心与椭圆几何中心一致，fd0≈fd，忽略相关函数简化导致的误差，利用欧拉公式可将相关函数表示为

黎美琪[2]分析宽带发射信号频谱不对称时提出单质点模型下宽带回波信号做复相关可得

相位偏差系数

是幅度和时延的函数，若相关时延为整数倍周期值，∆φ=0，即时延值估计准确，测速结果与频谱结构无关。椭圆回波信号相关函数中正弦函数为周期函数且周期为T=2π/wr2，若相关时延取值准确，即τ=NT，N为整数)，正弦函数趋于零，不对称频谱引入的频移偏差在相关中可完全去除，但实际相关时延一般取单次编码的时间长度τ=1/∆f，所以波束开角造成的频谱不对称影响测频结果出现偏差。

滤波器的中心频率一般设置为发射信号的中心频率，假设滤波器为理想低通滤波器，仅通带截止频率内的频点会通过滤波器，此时I=L。复自相关频率估计算法指出计算多普勒频移是对相关函数的相位进行估计[6]，相关函数的相位由虚部与实部比值的反正切得到

回波信号的相位误差∆φ=φ-2πfdτ，则频移误差∆f=f-fd，整理得测频偏差

其中，

忽略相关函数积分化简过程中引入的误差以及水底椭圆模型简化误差时，利用式(27)可计算波束开角导致的测频偏差。

3 仿真与试验数据分析

3.1 仿真实验

前文已经分析具有一定波束开角的水底椭圆散射模型下回波信号测频偏差受到波束开角的影响。不同方位扩展损失、散射强度的差异导致频谱不对称，测频结果偏小，且随波束开角增大，频谱不对称性增强，测频偏差增大。式(27)可计算波束开角导致的测频偏差，为验证测频偏差公式的准确性，将仿真实验结果与利用公式计算出的理论测频偏差值进行比较。改变波束开角范围[2◦,20◦]，其余仿真条件与图3 一致，对比仿真结果和公式计算的测频偏差，如图5 所示。之后固定波束开角分别为4◦、6◦，在频移为[0,300 Hz]时对比仿真结果与公式计算值，如图6所示。

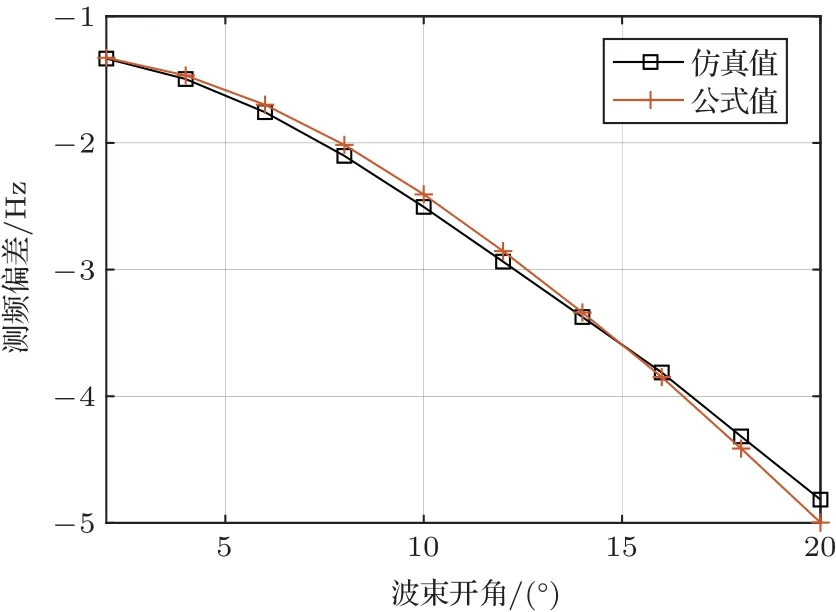
图5 不同波束开角下仿真值和公式值对比Fig.5 Comparison of simulation values and formula values under different beam angle

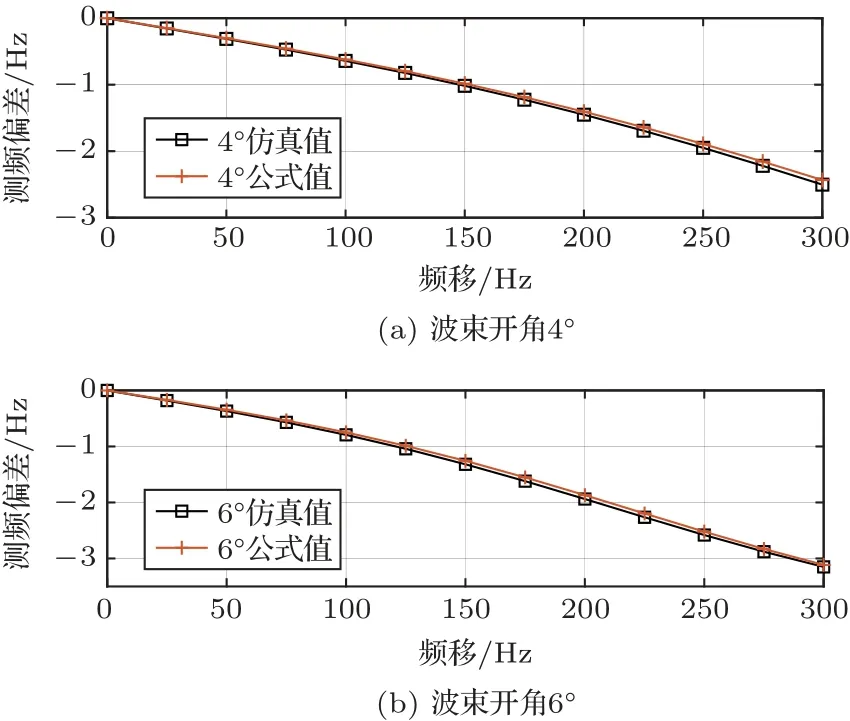
图6 不同频移下仿真值和公式值对比Fig.6 Comparison of simulation values and formula values under different Doppler shift

由图5 和图6 可知，任意波束开角下公式计算的理论值和仿真得到的测频结果均存在负偏差，这是由于足印右侧区域对应的传播距离、入射角均大于左侧，与此同时吸收损失与频率平方成正比，频率越高，吸收损失越大，导致水底回波信号频谱右侧能量少于左侧，测频结果偏小，测频偏差随着多普勒频移、波束开角增大而增大。由于相关函数简化误差和多普勒频移简化误差，公式理论值和仿真实验值存在些许差异，但总体吻合程度较好，证明了公式准确。

3.2 外场试验数据分析

2016 年5 月在外场试验中使用150 kHz 声学多普勒流速剖面仪(Acoustic Doppler current profiler,ADCP)进行测速试验，试验中固定发射信号编码码元数L=13，填充系数Q=6，在波束开角分别为4◦和6◦时进行试验，通过改变换能器大小来获得不同波束开角，换能器尺寸越大，波束开角越小。选择水底较平坦、速度变化较小的数据帧分析ADCP 相对于GPS 测速结果的偏差。同时在上述试验条件下利用式(27)计算理论测频偏差，通过试验所得ADCP 测速数据以及GPS 测速数据可计算实际测速偏差，将其与公式计算得到测频偏差比较，分析结果如表1所示。

表1 不同波束开角下实际测速偏差与公式计算值对比Table 1 Comparison of actual velocity measurement bias and formula values under different beam angle

表1 中实际测速偏差是ADCP 测速数据相对于GPS 测速数据未作标定时的测速偏差，对比4◦和6◦波束开角下GPS 速度和ADCP 速度可知，实际测速偏差和公式计算的理论测频偏差均为负值，波束开角增大时，实际测速偏差与公式计算的理论测频偏差呈现相同的变化趋势，即波束开角增大，测频偏差增大，与前文分析一致。由于测频偏差计算公式存在简化误差，且设备的基阵安装可能具有位置偏差，即实际波束主轴与设计的波束主轴方向存在夹角，因此理论测频偏差和实际结果有一定差异。

4 结论

具有一定波束开角的水底椭圆散射模型下，不同方位传播损失和散射强度存在差异，导致宽带回波信号频谱不对称，测频结果出现偏差，且偏差为负值。波束开角增大时，频谱不对称程度增强，测频偏差增大。通过仿真实验及外场试验数据证明了分析结论的正确性。针对波束开角对多普勒测频结果的影响，计划通过改善不对称频谱来修正测频偏差。